无传动间隙的3K行星齿轮减速器设计

王慰军 杨桂林 庆皓 陈庆盈

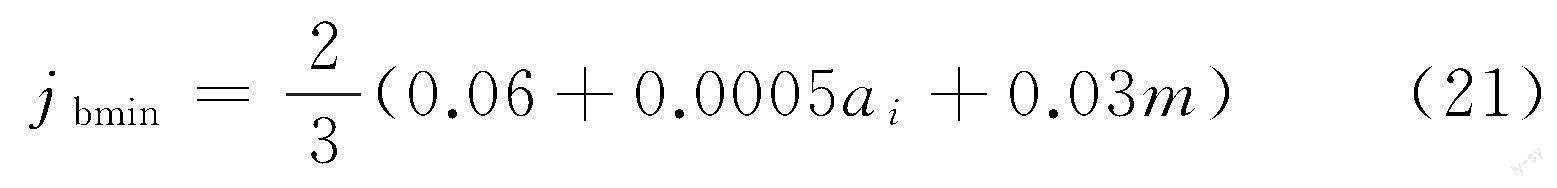
摘要：3K行星齿轮减速器的啮合齿轮副存在齿侧间隙，使得传动链中引入了传动间隙，导致传动精度降低以及换向冲击。为消除3K行星齿轮减速器的传动间隙，利用3K行星齿轮传动中行星架不参与力矩传递的特性，提出了一种柔性行星架以消除传动间隙，并通过仿真分析验证了所提消隙机构的有效性。通过配齿及效率优化实现了高效的正向和反向传动。研制样机并进行了传动精度、滞回特性、正弦响应误差、正向传动效率、反向传动效率以及反向启动扭矩测试，结果验证了所提柔性行星架对消除3K行星齿轮减速器传动间隙、提高传动精度和传动效率以及提高反向传动性能的有效性。

關键词：3K行星齿轮减速器；柔性行星架；反向传动；消隙；协作机器人

中图分类号：TP242.6

DOI：10.3969/j.issn.1004132X.2024.01.003

Design of 3K Planetary Gear Reducers with No Backlash

WANG Weijun1，2 YANG Guilin1，2 DU Qinghao1，2，3 CHEN Qingying1，2

1.Ningbo Institute of Material and Engineering Technology，Chinese Academy of Science，Ningbo，Zhejiang，315201

2.Zhejiang Key Laboratory of Robotics and Intelligent Manufacturing Equipment Technology，Ningbo，Zhejiang，315201

3.College of Material Science and Opto-Electronic Technology，University of Chinese Academy of Science，Beijing，100049

Abstract： Due to the presence of clearances in the gearing of 3K planetary gear reducers， transmission clearances were introduced into the transmission chain， resulting in a decrease in transmission accuracy and causing impacts during driving direction changes. By utilizing the characteristics that the carrier did not participate in torque transmission in 3K planetary gear transmission， a flexible planetary carrier was innovatively proposed to eliminate clearances of 3K planetary gear reducers， and the effectiveness of the proposed clearance elimination mechanisms was verified through simulation analysis. Gear matching and efficiency optimization were performed to achieve high forward and backward driving efficiency. Through the development of a prototype and testing of transmission accuracy， hysteresis characteristics， sinusoidal response error， transmission efficiency， and reverse starting torque， the effectiveness of the proposed flexible planetary carrier in eliminating clearances， transmission accuracy improvement， transmission efficiency and reverse transmission performance promoting was verified.

Key words： 3K planetary gear reducer； flexible carrier； back drivable； clearance elimination； collaborative robot

0 引言

随着机器人产业的快速发展，与人共融的协作机器人受到了广泛的关注。为了使协作机器人实现结构紧凑与轻量化，其驱动关节一般采用无框力矩电机和减速器驱动［1］。为减小电机的尺寸并实现轻量化，减速器通常采用大传动比，一般为100以上［2］。目前常见的减速器构型主要有谐波减速器、行星齿轮减速器和摆线针轮减速器这三种［3］。谐波减速器的传动精度高，但是其价格昂贵，传动效率低下（一般为65%左右），不支持反向传动，并且刚度较低［4］。行星齿轮减速器的承载能力大，传动效率高，支持反向传动，可实现大传动比，但由于齿轮副啮合存在齿隙，导致传动机构存在间隙，降低了它的传动精度［5］。摆线针轮减速器传动精度较高，但制造工艺复杂，承载能力较行星齿轮减速器弱［6］。

与传统工业机器人相比，协作机器人更注重人机交互性能［7］，因此其驱动关节所使用的减速器需具备良好的反向传动性能。当机器人与人或周围物体发生接触或碰撞时，优良的反向传动性能可以使机器人具备柔性，保证安全的人机交互。MATSUKI等［8］指出，随着减速器正向传动效率的提高，其反向驱动性能也可得到提高。AI［9］提出采用摩擦轮来替代行星传动中的齿轮，通过各摩擦轮接触传动替代齿轮副的啮合运动，消除了原先齿轮副齿侧间隙带来的传动间隙影响，实现了高精度传动和良好的反向传动性能，但它的缺点是承载能力较弱、容易打滑，并且需要定期对摩擦轮张紧以及提供特定的润滑。

3K行星齿轮减速器经配齿及优化设计，可实现大传动比以及高效传动［10］，如果能有效减小或消除传动间隙，那么它将是协作机器人驱动关节的理想减速器。OBA等［11］在普通3K行星齿轮减速器太阳轮、行星轮及内齿轮的同轴处各串联一个摩擦轮，利用摩擦传动减小了传动间隙，同时利用行星齿轮传动提高了承载能力和传动效率，但存在需定期对摩擦轮进行张紧的问题，并且由于尺寸及质量增大，导致整体的扭矩密度下降。JIANG等［12］采用双电机驱动来消除齿轮传动间隙，取得了良好的消隙效果，但由于需增加额外的驱动电机及传动链，使得整个传动系统变得复杂，且成本增加。综上所述，需要一种结构简单紧凑的消隙机构来减小或消除3K行星齿轮减速器的传动间隙，从而提高它的传动精度及传动效率，以满足协作机器人的驱动需求。

为此，笔者利用3K行星齿轮减速器的行星架不参与力矩传递的特性，创新设计了一种可有效消除传动间隙的柔性行星架，旨在提高3K行星齿轮减速器的传动精度与稳定性。通过仿真分析得到滞回特性曲线，验证了所提出消隙机构的有效性。经配齿及效率优化使其获得大传动比、高效的正向和反向传动，以满足协作机器人对驱动关节反向驱动的要求。最后研制了采用所提柔性行星架的3K行星齿轮减速器以及采用普通刚性行星架的3K行星齿轮减速器样机，并对其进行传动精度、滞回特性、正向和反向传动效率以及反向启动扭矩等测试。研究结果表明，所提柔性行星架可有效地消除传动间隙、提高传动精度、提高正向和反向传动效率以及反向传动性能。

1 行星减速器结构设计及效率分析

3K行星齿轮减速器可实现大传动比，通过配齿及变位系数优化可获得高效的正向和反向传动能力［13］。然而由于齿轮副齿侧间隙的存在，使得它具有传动间隙，降低了它的传动精度并带来了一定的换向冲击［14-15］。为此，需要从提高传动效率和消除传动间隙入手，以使其实现良好的反向传动能力以及高精度传动。

1.1 减速器传动机构设计

3K行星齿轮减速器的传动原理如图1所示，它由太阳轮、第一行星轮、第一内齿圈、第二行星轮、第二内齿圈和行星架所组成。其中太阳轮S、内齿圈R1和内齿圈R2同轴设置，内齿圈R1固定，行星轮P1与行星轮P2同轴固连。运动由太阳轮S输入，经内齿圈R1、行星轮P1及行星轮P2传动，内齿圈R2实现输出。整个传动机构形成三个啮合齿轮副，分别为行星轮P1与太阳轮S啮合、行星轮P1与内齿圈R1啮合及行星轮P2与内齿圈R2啮合。采用转化机构法，可得到3K行星齿轮减速器的传动比为

其中，Zj表示各齿轮的齿数，j∈{S，P1，R1，P2，R2}；I1=ZR1/ZS，I2=ZR1ZP2/（ZR2ZP1）；当ZR2ZP1和ZR1ZP2接近时，可以获得大传动比。当ZR1>ZR2时，I2<1，输入和输出方向相同；ZR11，输入和输出方向相反。

1.2 消隙机构设计

对3K行星齿轮传动机构进行受力分析，如图2所示。假设减速器的输入扭矩为TS，行星轮的个数为np，各啮合齿轮副受均载。此时太阳轮在一个功率分流上传递的扭矩T=TS/np。

太阳轮受到行星轮P1对其作用的圆周力为

FtP1S=2000T/s（2）

式中，s为行星轮直径。

太阳轮受到行星轮P1对其作用的径向力为

FrP1S=FtP1Stanα（3）

式中，α为齿轮压力角。

行星轮P1受到太阳轮S和内齿圈R1施加的圆周力分别为

FtSP1=FtP1S（4）

FtR1P1=FtR2P2-FtSP1（5）

行星轮P1受到太阳轮S和内齿圈R1施加的径向力分别为

FrSP1=FrP1S（6）

FrR1P1=FtR1P1tanα（7）

行星轮P2受到内齿圈R2施加的圆周力为

FtR2P2=FtR1P1+FtSP1（8）

行星轮P2受到内齿圈R2施加的径向力为

FrR2P2=FtR2P2tanα（9）

根据静力平衡关系可得

FtR1P1+FtSP1-FtR2P2+FtH=0（10）

行星架H受到的圆周力FtH=0，径向力为

FrH=FrR1P1+FrR2P2-FrSP1（11）

因此，行星架H所受到的扭矩TH=0。由此可見，3K行星齿轮减速器的行星架不参与力矩传递，只起到使行星轮实现均载和辅助支承行星轮的作用。

为消除3K行星齿轮减速器的传动间隙，提高其传动精度，利用其行星架不参与力矩传递只起辅助支撑的特性，设计图3所示的柔性行星架作为消隙机构来消除3K行星齿轮减速器的传动间隙。它由两个可相对转动的行星轮轴安装支座、调整块、调节螺钉以及连接两个支座的弹簧片所组成。

具体消隙原理如图4所示。通过调节螺钉调整弹簧片预紧量来实现两个行星轮轴安装支座之间张角的变化，使相邻两个行星轮的位置绕太阳轮轴线沿圆周方向背对背转动一个微小角度，让它们分别与太阳轮和内齿圈的齿面向预紧方向贴紧，从而形成消隙齿轮对，而各啮合齿轮副的中心距仍保持不变。此时，无论太阳轮正转或反转，3K行星齿轮减速器都可实现无传动间隙的运动输出，提高了3K行星齿轮减速器的传动精度与平稳性。通过在柔性行星架上均匀设置4个双联行星轮，即可组成两个消隙齿轮对，以确保3K行星齿轮减速器传动平稳。

1.3 减速器传动效率分析

为实现高效传动，对3K行星齿轮减速器的正向和反向传动效率进行分析，以得到影响传动效率的主要因素，并针对此进行效率优化，以提高3K行星齿轮减速器的传动效率，使其具备良好的反向传动性能。采用啮合功率法［16］，得到3K行星齿轮减速器的正向传动效率ηF和反向传动效率ηB，表达式如下：

其中，ηa、ηb、ηc分别为太阳轮S与行星轮P1、行星轮P1与内齿圈R1以及行星轮P2与内齿圈R2这三个齿轮副的基本啮合效率，可表示为［17］

其中，μ为齿轮副之间的摩擦因数；Zi1、Zi2分别为齿轮副中主动齿轮和被动齿轮的齿数；sgni为啮合状态系数（内啮合为-1，外啮合为1）；εi为关于齿轮副啮入和啮出重合度的函数，可表示为［17］

式中，εi1、εi2分别为齿轮副的啮入与啮出重合度；αwi为齿轮的啮合角；inv（αwi）表示渐开线函数；αai1、αai2分别为齿轮副中主动和被动齿轮的齿顶圆压力角；m为齿轮的模数；Xij为齿轮副中各齿轮的变位系数；Δy为齿顶高变动系数。

综合式（12）～式（20），3K行星齿轮减速器的正向传动效率和反向传动效率是关于齿轮副摩擦因数、各齿轮齿数及其变位系数的函数。设置传动比和齿数范围，采用遍历算法，得到了传动比从40至150的效率分布，如图5所示。选取所需的传动比后，就可以以变位系数为设计变量，设置3K行星齿轮减速器装配、同轴以及邻接为约束条件，以传动效率最高为目标函数进行3K行星齿轮减速器传动效率的优化。在正向传动效率得到提高的同时，其反向传动效率也可实现优化，从而提高它的反向传动性能。

2 消隙过程仿真分析

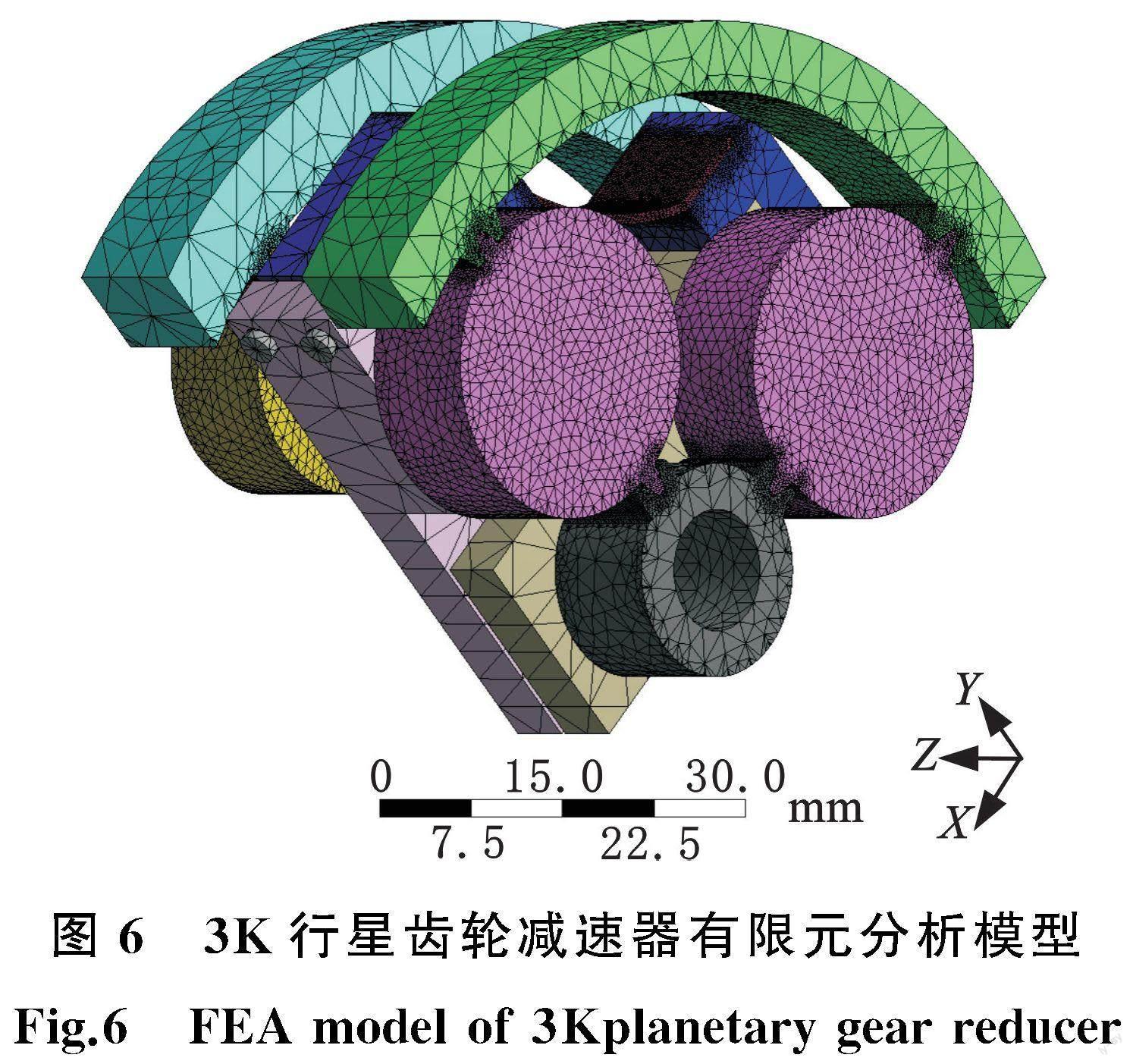
为验证柔性行星架对消除3K行星齿轮减速器传动间隙的有效性，采用ANSYS有限元软件来进行消隙过程的仿真分析。考虑3K行星齿轮减速器的对称性，取其一半作为分析模型。保留各啮合齿轮副，忽略其余齿部的细节，以提高计算效率，建立的有限元分析模型如图6所示。

单元采用Solid187，网格数量为252 528，节点数量为423 404，齿轮副最小侧隙公式［18］为

式中，ai为各啮合齿轮副的中心距。

同时综合考虑后续样机齿轮制造给定的公法线长度变动公差及齿厚偏差，设置各齿轮副的初始单侧间隙为0.03 mm，如图7所示，啮合部位网格尺寸设定为0.2 mm。其中边界条件设置为：两个内齿圈采用固定约束，其余齿轮均保留绕自身轴线的旋转自由度，同时允许行星轮随行星架绕太阳轮轴线转动。

分别设置行星轮安装座的调整位移量为0.01 mm至0.05 mm之间，步长增量为0.01 mm，以控制相邻两个行星轮安装座之间的张角，使相邻两个行星轮与太阳轮及内齿圈的单侧齿隙沿弹簧预紧方向减小。经计算分析，获得3K行星齿轮减速器各啮合齿轮副在不同调整位移量时的啮合状态，其中调整量为0.05 mm时，各构件相对位置变化如图8所示。

各齿轮副的啮合状态如图9所示。各行星轮沿圆周方向的位移量为0.027 mm，左侧行星轮与太阳轮以及内齿圈啮合齿轮副之间的左侧间隙已基本消除；相邻行星轮与太阳轮以及内齿圈啮合副之间的右侧间隙已基本消除。随着调整量的增大，其双向传动间隙可完全消除。此时，3K行星齿轮减速器就可以实现无传动间隙的双向传动。

在太阳轮处施加幅值大小为0.2 N·m、时间为15 s的斜坡扭矩载荷，此时太阳轮转动的角度即为减速器的传动误差。通过绘制3K行星齿轮减速器的输入扭矩与传动误差之间的关系，可获得减速器在启动及换向时的静态特性，仿真结果如图10所示。随着调整位移量δ的增大，传动死区逐渐缩小，低刚度区出现。当调整位移量达到0.05 mm时，传动死区转变为低刚度区，传动间隙消除。验证了所设计的柔性行星架对消除3K行星齿轮减速器传动间隙的有效性。

3 样机研制与性能测试

考虑样机尺寸小、结构紧凑，从图5所示的结果中选取传动比为54.72的齿轮参数来进行3K行星齿轮减速器样机设计。通过优化各齿轮的变位系数后，其正向计算传动效率和反向计算传动效率分别达到85.6%和81.7%，具体参数如表1所示。

采用柔性行星架以及普通刚性行星架，完成两种3K行星齿轮减速器样机的装配，对这两种样机分别进行传动误差、滞回特性、正弦响应误差、正向与反向传动效率以及反向启动扭矩的测试。其中反向启动扭矩测试中，为进行对比，加入了对谐波减速器的测试。所有齿轮模数均取1 mm，材料采用38CrMoAl合金钢，并进行氮化处理；行星架和外壳等主要零件材料采用7075铝合金，所完成的3K行星齿轮减速器样机如图11所示。

3.1 传动误差测试

3K行星齿轮减速器传动误差的测试平台如图12所示。伺服电机与3K行星齿轮减速器输入轴之间串联安装绝对式编码器，3K行星齿轮减速器的输出轴端串联安装绝对式编码器，以实时检测3K行星齿轮减速器的输入与输出转角。通过伺服电机带动减速器的输入轴转动，传动误差可根据3K行星齿轮减速器输入转角、输出转角与传动比之间的关系表示如下：

θerror=θoutGSR2-θin（22）

式中，θerror为3K行星齿轮减速器的传动误差；θin为3K行星齿轮减速器的输入转角；θout为3K行星齿轮减速器的输出转角。

在测试过程中，伺服电机输入恒定转速50 r/min，以3K行星齿轮减速器输出一转为采样周期，在无负载的条件下进行传动误差测试。分别测试了采用柔性行星架的3K行星齿轮减速器和采用刚性行星架的3K行星齿轮减速器两种样机，测试结果如图13所示。其中采用普通刚性行星架的3K行星齿轮减速器的最大传动误差为9.25′，而采用柔性行星架的3K行星齿轮减速器的最大传动误差为4.01′，減小了57%。

由此可见，所设计的柔性行星架可以在一定程度上补偿3K行星齿轮减速器的制造和装配误差，极大地提高了3K行星行星齿轮减速器的传动精度。

3.2 滞回特性测试

搭建3K行星齿轮减速器的滞回特性测试平台，如图14所示。在3K行星齿轮减速器的输入和输出端分别安装力矩传感器和编码器，以检测输入端和输出端的力矩和转角位置。将3K行星齿轮减速器的输出端固定，伺服电机与3K行星齿轮减速器输入端串联安装，并以力矩控制模式运行。

为分析减速器的滞回特性，给伺服电机以幅值0.2 N·m、周期50 s的力矩运行指令。为确保准静态测试效果，将电机最大转速限制为0.5 r/min。传动间隙可通过输入力矩为零时的传动误差差值获得。

采用普通行星架的3K行星齿轮减速器的输入扭矩与传动误差的关系如图15a所示，可见它存在较为明显的传动死区，传动间隙为16.71′。而采用柔性行星架的3K行星齿轮减速器的输入扭矩与传动误差的关系如图15b所示，它的传动间隙仅为0.52′。因此，所设计的柔性行星架可以有效地消除3K行星齿轮减速器的传动间隙。

3.3 正弦响应误差测试

采用图12所示的测试平台，分别对采用柔性行星架和普通行星架的两种3K行星齿轮减速器样机进行正弦响应误差测试。通过电机对3K行星齿轮减速器输入轴输入正弦位置信号，除以减速比GSR2后得到其理论输出位置响应曲线，由安装在3K行星齿轮减速器输出端的编码器获取实际输出位置响应曲线，结果如图16所示。由图16可见，采用普通行星架的3K行星齿轮减速器由于存在较大的传动间隙的响应误差为7.72′，正向周期输出响应几乎完全消失。而采用柔性行星架的3K行星齿轮减速器的响应误差仅为0.68′，可以很好地对输入进行响应。

3.4 反向启动扭矩测试

为验证采用柔性行星架的3K行星齿轮减速器具有良好的反向传动性能，搭建图17所示的测试平台，对其进行反向启动扭矩的测试。其中，与电机直连的减速器与被测3K行星齿轮减速器的输出轴串联安装，在减速器与被测3K行星齿轮减速器输出轴之间设置扭矩传感器，以检测该3K行星齿轮减速器输出轴转动时的扭矩。伺服电机以不高于70 r/min的速度运行，经减速比为35的减速器传动，使被测3K行星减速器输入轴以不高于2 r/min的速度运行，当被测3K行星齿轮减速器输出轴转动时，将此时扭矩传感器的读数作为反向启动扭矩。为进行对比，引入对谐波减速器的反向启动扭矩测试，谐波减速器的型号为LHSG-25-50。

结果如图18所示，测得谐波减速器的反向启动扭矩为15.83 N·m，采用刚性行星架的普通3K行星齿轮减速器的反向启动扭矩为1.59 N·m，而采用柔性行星架的3K行星齿轮减速器的反向启动扭矩为0.91 N·m。

由此可见，谐波减速器的反向启动扭矩为普通3K行星齿轮减速器的9.96倍，是采用柔性行星架3K行星齿轮减速器的17.4倍。因此，3K行星齿轮减速器的反向启动扭矩要远小于谐波减速器的反向启动扭矩。同时，通过纵向比较装备刚性和柔性行星架的两种3K行星齿轮减速器发现，采用所设计的柔性行星架后，3K行星齿轮减速器的反向启动扭矩降低了42.6%。所以，采用柔性行星架的3K齿轮减速器具有更优良的反向传动性能。

3.5 传动效率测试

搭建图19所示的3K行星齿轮减速器正向传动效率测试平台。3K行星齿轮减速器的传动效率可表示为输出功率与输入功率的比值。因此，可用输入扭矩、输入转速及输出扭矩、输出转速表示如下：

3K行星齿轮减速器在传动过程中传动比基本保持恒定，通过测量被测减速器输入轴端的扭矩以及输出轴端的扭矩，再根据式（23），可以得到被测3K行星齿轮减速器的正向传动效率。伺服电机输出轴通过联轴器和被测3K行星齿轮减速器的输入轴连接，磁粉制动器输出轴通过联轴器与被测3K行星齿轮减速器的输出轴连接，用以施加指定的负载力矩。在被测3K行星齿轮减速器的输入轴和输出轴上串联安装力矩/转速传感器，以检测输入轴与输出轴上的扭矩和转速。

3K行星齿轮减速器的反向传动效率测试平台如图20所示。伺服电机经减速器带动被测3K行星齿轮减速器输出轴转动。在被测3K行星齿轮减速器输入轴和磁粉制动器输出轴之间串联安装力矩/转速传感器，用以检测被测3K行星齿轮减速器输入端的扭矩和转速。伺服电机输出轴上的减速器与被测3K行星齿轮减速器的输出轴之间串联安装力矩/转速传感器，以检测被测3K行星齿轮减速器输出端的扭矩和转速。根据式（23）可以得到被测3K行星齿轮减速器的反向传动效率。

测试正向传动效率时，电机以100 r/min的步长增量从100 r/min到900 r/min输入转速，磁粉制动器以5 N·m的步长增量从5 N·m到50 N·m施加负载扭矩。这样就可以得到由9种转速和10种负载扭矩所组成的90个测量点。在测试反向传动效率时，电机以2 r/min的步长增量从2 r/min到16 r/min输入转速，磁粉制动器以0.05 N·m的步长增量从0.05 N·m到0.4 N·m施加负载扭矩，这样就形成了由8种电机转速和8种负载扭矩所组成的64个测量点。

采用柔性行星架的3K行星齿轮减速器的传动效率测试结果如图21所示，横坐标表示电机输入的转速nin，纵坐标为所施加的负载转矩Tload。最大正向传动效率和反向传动效率分别为80%和65%。

采用刚性行星架的3K行星齿轮减速器的正向传动效率和反向传动效率分别为75.99%和59.11%。因柔性行星架在一定程度上可以补偿行星轮的位置偏差，以及改善行星轮的均载性能，减小摩擦，所以，柔性行星架可以提高3K行星齿轮减速器的双向传动效率。

所测得的传动效率低于表1所示的理论计算效率值，主要是由于樣机的齿轮和行星架等零件存在制造误差，导致齿轮副的啮合效率降低，各行星轮的均载性能变差，摩擦增大，从而影响了3K行星齿轮减速器装配后的传动效率。实际应用时，可通过提高齿轮和行星架制造和装配精度以及采用高性能润滑脂来确保3K行星齿轮减速器达到或接近理论计算传动效率。

4 结论

针对3K行星齿轮减速器存在传动间隙问题，创新提出了一种柔性行星架，减小了3K行星齿轮减速器的传动间隙，提高了其传动精度、传动效率与反向传动性能。得到结论如下：

（1）采用柔性行星架并进行侧隙调整后，3K行星齿轮减速器的传动间隙由原来的16.71′减小到0.52′；其传动误差由9.25′减小到4.01′；正弦响应误差由7.72′减小到0.68′。结果表明，采用柔性行星架可以有效提高3K行星齿轮减速器的传动精度，验证了所提出的柔性行星架对减小传动间隙、提高3K行星齿轮减速器传动精度的有效性。

（2）采用柔性行星架后，3K行星齿轮减速器的正向传动效率由75.99%提高到80%，其反向传动效率由59.11%提高到65%。因柔性行星架在一定程度上可以补偿行星轮的位置偏差，改善了均载性，所以采用柔性行星架的3K行星齿轮减速器的正向和反向传动效率有小幅提高。由此可知，柔性行星架有助于提高3K行星齿轮减速器的正向和反向传动效率。

（3）通过反向启动扭矩测试，验证了采用柔性行星架的3K行星齿轮减速器具有良好的反向传动性能。

下一步将对所设计的3K行星齿轮减速器与无框力矩电机进行集成，完成双向驱动关节的研制，以提升协作机器人的反向驱动性能，从而使协作机器人实现无力传感器的柔顺控制。

参考文献：

［1］ OBA S， FUJIMOTO Y. Hybrid 3K Compound Planetary Reduction Gearbox with a Roller Transmission Mechanism［J］. IEEE/ASME Transactions on Mechatronics， 2022， 27（4）：2356-2366.

［2］ CRISPEL S， GARCIA P L， SAERENS E， et al. A Novel Wolfrom-based Gearbox for Robotic Actuators［J］. IEEE/ASME Transactions on Mechatronics， 2021， 26（4）：1980-1988.

［3］ ISHIDA T， TAKANISHI A. A Robot Actuator Development with High Back Drivability［C］∥2006 IEEE Conference on Robotics. Bangkok， 2006：1-6.

［4］ DU Q， ZHANG T， YANG G， et al. A Review of Powered Back Drivability of Robot Actuators for Human-robot Interaction［C］∥2021 IEEE 16th Conference on Industrial Electronics and Applications. Chengdu， 2021：1115-1120.

［5］ NABESHIMA C， AYUSAWA K， HOCHBERG C， et al. Standard Performance Test of Wearable Robots for Lumbar Support［J］. IEEE Robotics and Automation Letters， 2018， 3（3）：2182-2189.

［6］ KOBUSE D， FUJIMOTO Y. Efficiency Optimization of High-reduction-ratio Planetary Gears for Very High-power Density Actuators［C］∥2016 IEEE 25th International Symposium on Industrial Electronics（ISIE）. Santa Clara， 2016：1240-1245.

［7］ KANAI Y， FUJIMOTO Y. Torque-sensorless Control for a Powered Exoskeleton Using Highly Back-drivable Actuators［C］∥44th Annual Conference of the IEEE Industrial Electronics Society. Washington D C， 2018：5116-5121.

［8］ MATSUKI H， NAGANO K， FUJIMOTO Y， et al. Bilateral Drive Gear—a Highly Back Drivable Reduction Gearbox for Robotic Actuators［J］. IEEE/ASME Transactions on Mechatronics， 2020， 24（6）：2661-2673.

［9］ AI Xiaolan. Development of Zero-spin Planetary Traction Drive Transmission：Part 1—Design and Principles of Performance Calculation［J］. Journal of Tribology， 2002， 124（2）：386-391.

［10］ 許锦茂. 渐开线齿轮行星传动的设计与制造［M］. 北京：机械工业出版社， 2002.

XU Jinmao. Design and Manufacturing of Involute Gear Planetary Transmission［M］. Beijing：Mechanical Industry Press， 2002.

［11］ OBA S， FUJIMOTO Y. 3K Compound Planetary Reduction Gearbox with Non-backlash Mechanism［C］∥IEEE 16th International Workshop on Advanced Motion Control（AMC）. Kristiansand， 2020：207-212.

[HT5"SS][JY]（[HTH]下转第55页[STBZ][HTSS]）

[HT5"SS]（[HTH]上接第44页[STBZ][HTSS]）[HT]

［12］ JIANG H， FU H， HAN Z， et al. Elimination of Gear Clearance for the Rotary Table of Ultra Heavy-duty Vertical Milling Lathe Based on Dual Servo Motor Driving System［J］. Applied Sciences， 2020， 10（11）：4050.

［13］ KANAI Y， FUJIMOTO Y. Performance Analysis of Torque-sensorless Assist Control of a Powered Exoskeleton Using Highly Back-drivable Actuators［C］∥2019 IEEE 17th International Conference on Industrial Informatics. Helsinki， 2019：577-582.

［14］ ZIMULDINOV E， BYKOV A， CLERSKIKH E， et al. Calculation and Development of 3k Planetary Gearbox with Non-standard Gear Modules［C］∥2020 4th International Conference on Electronics， Materials Engineering &Nano-technology（IEMENTech）. Kolkata， 2020：1-6.

［15］ AKIYAMA N， FUJIMOTO Y. Highly Efficient 2K-H Compound Planetary Reduction Gearbox Using Balancer［C］∥Conference of the IEEE Industrial Electronics Society. Lisbon， 2019：669-674.

［16］ 饒振纲. 行星传动机构设计［M］. 北京：国防工业出版社， 1994.

RAO Zhengang. Design of Planetary Gear Mechanism［M］. Beijing：National Defense Industry Press， 1994.

［17］ 崔丽， 秦大同， 石万凯. 行星齿轮传动啮合效率分析［J］. 重庆大学学报（自然科学版）， 2006（3）：11-14.

CUI Li， QING Datong， SHI Wankai. Reference Efficiency of Planetary Gear Train［J］. Journal of Chongqing University（Natural Science）， 2006（3）：11-14.

［18］ 成大先. 机械设计手册（第五版， 第3卷）［M］. 北京：化学工业出版社， 2008.

CHENG Daxian. Handbook of Mechanical Design（5th edition， vol3）［M］. Beijing：Chemical Industry Press， 2008.