静力荷载作用下微观负泊松比锚杆的本构模型
2024-02-06陶志刚崔龙飞
张 伟,赵 亮,,陈 峰,陶志刚,崔龙飞
(1.河南科技大学 土木建筑学院,河南 洛阳 471023;2.南阳理工学院 河南省冲击与工程结构灾害动力学国际联合实验室,河南 南阳 474150;3.中国矿业大学(北京) 力学与建筑工程学院,北京 100083;4.洛阳爱众人力资源服务有限公司 工程技术部,河南 洛阳 471000)
0 引言
锚杆是当代煤矿支护中的常用构件,具有增强围岩承载力、支护方式简单、机械化程度高且成本相对较低等优点[1-2],已广泛运用于隧洞、边坡、地下巷道等工程支护中。
随着人们对于资源需求的不断增加,浅层资源已不能完全满足需求,使得人们不得不在深层进行资源开采。与浅层资源开采不同,随着开采深度的不断增加,在深部资源开采中往往会遇到高应力、大变形等复杂的力学环境[3-4]。采用传统锚杆对其进行支护,存在因材料失效而带来严重的施工灾害问题。故国内外相继研发了多种吸能锚杆,其中具有代表性的锚杆有锥型锚杆[5]、H型锚杆[6]、D型锚杆[7]、Garford锚杆[8]、新型让压管锚杆[9]、J型锚杆[10]等。这些锚杆都属于传统泊松比材料,力学特性较为单一,在实际工程中难以满足深层围岩高应力、大变形环境灾害控制要求[11]。针对上述问题,文献[12-13]自主研发了宏观负泊松比(negative Poisson’s ratio,NPR)锚杆,这是一种具有负泊松比效应、高恒阻力、大变形且能抗冲击的新型锚杆,在公路隧洞支护[14]、冲击地压控制[15]、深埋软岩巷道[16]、大型露天矿滑坡监测预警[17]等工程中得到了广泛应用。
随后,文献[18]基于宏观NPR材料又提出了微观NPR材料的概念,认为需满足3个条件:(1)泊松比值达到10-2量级;(2)应变值大于25%;(3)无明显屈服平台。微观NPR锚杆具有较强的抗剪性能和较高的延性[19-20],但对微观NPR锚杆超常的力学特性研究还处于初步阶段,其相应的本构模型尚不明确,传统的本构模型难以适用。故本文利用万能试验机,对微观NPR锚杆开展静力拉伸试验,获取锚杆的荷载位移、应力应变等关系曲线;利用数字图像相关(digital image method,DIC)技术,对整个试验过程进行实时拍摄和数据记录;基于试验结果建立相应的本构模型,可为微观NPR锚杆在工程应用及其他方面的研究提供参考。
1 微观NPR锚杆拉伸试验
1.1 试验材料及准备
试验所用的原材料是由同一根直径为18 mm的微观NPR棒材打磨而成,具有较好的一致性。为了获取材料的应力应变关系曲线,按照静力拉伸标准试样进行加工的光滑圆棒如图1(其中,图1a为加工试样图,图1b为实物图)所示。光滑圆棒试样总长为120 mm,并在两端加工螺纹以便于夹具固定。对试样中间拉伸段的上端、中间、下端直径进行测量,如表1所示,可以看出本批次加工的试样较好。为防止试验结果的偶然性,对微观NPR锚杆静态拉伸进行了2次平行试验,在试验开始前对试样中间拉伸段喷上哑光白漆,人为制作散斑点,便于在试验中观察试样拉伸的全过程。

表1 试样拉伸段直径 mm

(a) 加工试样图 (b) 实物图
1.2 试验设备及过程
本试验在日本岛津公司所生产的AG-X plus万能材料试验机上进行,最大负载为100 kN。引伸计标记段为25 mm,放置在试样的中间位置,在万能试验机前放置1台电荷耦合器件(charge coupled device,CCD)相机,并在两端各放置一台补光灯,以确保实验过程中所拍摄的照片清晰,设置相机拍摄速率为1张/s,从试验开始直至试样断裂连续不间断进行拍摄。试验过程按照GB/T 228.1—2021《金属材料拉伸试验 第1部分:室温试验方法》实施。本试验在室温25 ℃的环境下进行,在正式试验前单独用1个试样对万能材料试验机进行测试,确保无异常后,开始正式试验。采用位移控制的方式来施加荷载,根据试样的尺寸设置拉伸速度为1 mm/min,得到的名义应变率为6.67×10-4s-1。直至试件断裂或荷载从最大值迅速下降,自动停止加载,记录试验过程中完整的荷载位移关系。在试验加载过程中采用引伸计来获取试样标记段位移随时间变化的相关数据;试验结束后对试样进行封装,以确保试验具有可追溯性。试验设备放置如图2所示。

图2 试验设备
2 微观NPR锚杆拉伸试验结果
2.1 荷载位移关系曲线
通过万能试验机和引伸计来记录微观NPR锚杆在拉伸过程中的荷载位移关系,进而获取应力应变关系曲线,试验结果分别如图3和图4所示。从图3中可以看出:两次试验的荷载位移关系曲线走势基本保持一致,说明本批次试件的重复性好,结果可靠。从图4中可以看出:在静载作用下微观NPR锚杆从拉伸到破坏可分成3个阶段,分别为弹性阶段、恒阻大变形阶段和破坏阶段,在整个拉伸过程中没有出现明显的屈服平台,从弹性阶段直接进入恒阻大变形阶段,在AB弹性阶段中,荷载和位移近似呈直线上升,处于线弹性阶段;进入BC恒阻大变形阶段后均匀伸长,有较好的延展性,并且随着应变的不断增加,应力上升不显著;到达应力最高点后进入CD破坏阶段,应力逐渐下降,直至断裂。微观NPR锚杆的整个拉伸过程中恒阻大变形阶段持续时间最长,占到了整个拉伸段内的82.2%。静载作用下的微观NPR锚杆拉伸试验数据如表2所示,可以得出:最大拉伸长度为15.39 mm,平均伸长率为61.19%;所能承受的最大荷载为27.08 kN,平均值为27.08 kN,反映出微观NPR锚杆具有高应力和高均匀延性的力学特性。

表2 静力拉伸试验数据
2.2 DIC等效应变云图分析
本次试验采用CCD相机拍摄,并通过DIC技术进行计算,得到微观NPR锚杆等效应变云图,如图4所示。从屈服点的等效应变云图中可以看出,试样拉伸时的应变基本上无明显变化;随着施加的位移不断加大,达到破坏点时,试样应变规律基本上呈现均匀分布,且应变差值相差较小,也进一步说明了微观NPR锚杆在恒阻大变形阶段呈现均匀受拉,在试件中间出现拉伸应变集中带,可以预测试样断裂的位置在红色区域范围内;随着位移的继续增加,在断裂前一刻的应变云图中可以看出,中间应变最大,试样的断裂位置在颜色最深的区域中。DIC等效应变云图的整个拉伸过程反映出微观NPR锚杆具有高延性的力学特性。
材料在不断拉伸过程中出现集中变形的现象称为颈缩[21]。传统材料大多数都会出现明显的颈缩现象,但从微观NPR锚杆断裂前一刻的应变云图可以看出,断裂处位移与上下两端的位移无明显变化,反映了微观NPR锚杆无明显颈缩的力学特性。
3 微观NPR锚杆本构模型
3.1 微观NPR锚杆恒阻大变形阶段本构模型
对于无明显屈服平台的应力应变关系曲线通常采用Johnson-Cook(JC)本构模型[22]来建立相应的本构关系。JC本构模型具有形式简单、通用性强及材料系数易于拟合等优点,普遍用于有限元数值模拟中。
JC本构模型是由文献[23]提出的,其表达式如式(1)所示:
(1)
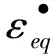
JC本构模型由3部分组成:左边部分为常温状态下的塑性应变,不涉及应变率和温度;中间部分为应变率影响系数;右边部分为温度影响系数。对于本次光滑圆棒的静载拉伸试验,不考虑温度和应变率的影响,故可将JC本构模型表达式简化为:
(2)
此时只需对本构模型(2)中的A、B、n进行相应的参数赋予,即可得到微观NPR锚杆的弹性阶段和恒阻大变形阶段的本构模型。
对应力应变关系曲线中的弹性阶段进行拟合可以得到微观NPR锚杆的弹性模量E=140 GPa。微观NPR锚杆在整个拉伸的过程中没有出现明显的屈服平台,取塑性应变0.2%所对应的应力为屈服强度即σ=595.13 MPa。最大荷载对应的应力和应变可认为是破坏时的应力和应变,即应力为957.51 MPa,应变为0.52。所获得的微观NPR锚杆的力学性能参数如表3所示。

表3 微观NPR锚杆的力学性能参数
通过万能试验机所得到的应力应变关系曲线为工程应力应变,需要将其转化的真实应力应变。在体积不发生改变的情况下,工程应力应变与真实应力应变存在以下关系:
σe=σ(1+ε);
(3)
εe=ln(1+ε),
(4)
其中:σe为真实应力,MPa;εe为真实应变;σ为工程应力,MPa;ε为工程应变。
本文选取试样1的应力应变关系建立相关的本构模型,通过式(3)和式(4)进行换算,可得到试样1的真应力应变关系。故硬化系数B和硬化指数n需在真实应力应变关系曲线中拟合屈服点到破坏点之间的工程应力应变数据得到。得到B=1 917.0 2 MPa,n=0.87。微观NPR锚杆恒阻大变形阶段的JC本构模型如式(5)所示:
(5)
3.2 微观NPR锚杆破坏阶段本构模型
文献[24]指出JC本构模型只能适用破坏点之前阶段,对于破坏阶段的本构模型参照文献[25]中所提出的方法,在破坏点处需进行分段处理,故对JC本构模型进行修正,其表达式如(6)所示:
σeq=σu[ω(1+εeq-εu+A/E)+(1-ω)(εeq/εu)εu],ε≥εu-A/E,
(6)
其中:σu为破坏点处的真实应力,MPa;εu为破坏点处的真实应变;ω为材料参数,取值为0~1。当ω取1时,破坏点后的本构模型呈线性关系,当ω取0时破坏点后的本构模型呈幂函数关系。当ω为0~1时,将两者线性结合,对比有限元模拟中参数ω不同取值的计算结果与试验结果,从中选取与试验曲线最接近的数值,即为该材料的参数。
3.3 微观NPR锚杆断裂参数标定
上述所建立的本构模型,在有限元中进行拉伸仿真过程中并不会出现断裂,故在确定本构模型后需要对其进行断裂参数的标定。通常情况下断裂参数由断裂应变和应力三轴度两部分组成,其中,光滑圆棒试样拉伸试验中应力三轴度为1/3,断裂应变可由试验前后的直径变化测得,其表达式如(7)所示:
εf=2ln(d0/df),
(7)
其中:εf为断裂应变;d0为断裂前试样直径,mm;df为断裂时断裂区域断口直径,mm。对微观NPR锚杆断裂后的断口直径进行测量,并计算断裂应变结果,如表4所示。

表4 微观NPR锚杆的断口直径和断裂应变
4 有限元模拟
4.1 有限元模型
采用ABAQUS/CAE软件建立数值模型,进行静力荷载作用下微观NPR锚杆拉伸的数值仿真模拟研究。首先按照试样的标准尺寸图建立如图5所示的有限元模型,并将试样的材料参数以及本构模型输入到模型中,并在模型的左右两侧各设置一个参考点,将左右两端的参考点与试样的夹持段分别进行耦合,设置边界条件为左侧完全固定,限制所有位移,右侧通过控制位移的方式来施加载荷,试验中只是对引伸计的上下两个夹头的位移进行了记录,故需要对整个试样的拉伸位移进行调大。选取显示动力学进行分析,分析步为1 600步,每步位移为0.016 mm,总位移为25.6 mm。单元类型采用C3D8R,8节点6面体线性缩减积分单元。由于中间段拉伸破坏的关键位置,故需要对该区域进行加密,将网格尺寸设置为0.5 mm×0.5 mm,两端可以将网格尺寸适当稀疏,设置为1 mm×1 mm。模型总共包含48 000个单元,53 456个节点。在历史变量里输出右端的支反力,并将中间拉伸段25 mm处的上、下2个点设置为关键点,来充当试验过程中引伸计的作用,输出2个关键点的水平位移关系,设置等间隔输出数据为200个,即可以得到微观NPR锚杆静力拉伸的仿真荷载位移关系曲线并与试验结果进行比较。

图5 微观NPR锚杆有限元模型图
4.2 模拟结果及分析
通过有限元软件模拟静力荷载下微观NPR锚杆拉伸过程,对只采用JC本构模型和对破坏阶段中调整不同ω的取值的本构模型进行了计算,对比所得到的数值模拟结果与试验结果,如图6所示。图6中,试样1表示试验的荷载位移关系曲线,从图6中可以看出,只采取JC本构模型来建立微观NPR锚杆的本构模型,在弹性阶段和恒阻大变形阶段可以较为准确地表达,但在破坏阶段后呈现不断上升的趋势。故需要对破坏点后采用修正的本构模型,通过调整破坏阶段本构关系中ω的取值可以看出,随着ω的取值不断减小,破坏阶段的曲线有逐渐往下走的趋势。最后得出当ω取值为0时,有限元模拟结果与试验所得到的荷载位移关系曲线基本吻合。即得到了微观NPR锚杆分段的本构模型,如式(8)所示:
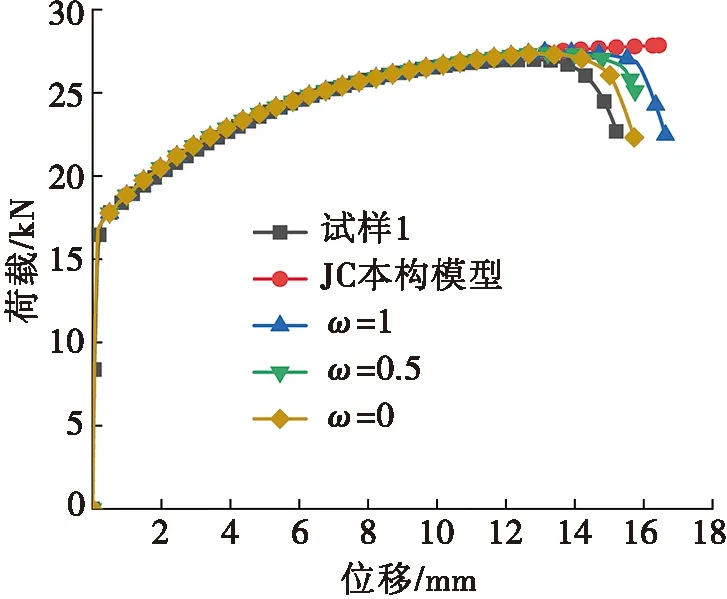
图6 试验与有限元荷载位移关系曲线
(8)
本文所建立的微观NPR锚杆的本构模型,可以用更加简洁的形式来描述其相应关系,这为微观NPR锚杆在实际工程的应用提供了方便,也为在其他方面的力学研究提供参考。
5 结论
(1)微观NPR锚杆的力学特性表现为以下4个方面:拉伸过程中,没有明显的屈服平台;拉伸全过程表现为均匀拉伸变形;有较强的延伸率;断裂后无明显颈缩现象。
(2)通过应力应变关系曲线,以0.2%塑性应变所对应的强度得出了微观NPR锚杆的屈服强度为σ=595.13 MPa,最大抗拉强度为σ=957.51 MPa,弹性模量为E=140 GPa。
(3)所建立的微观NPR锚杆本构模型可以准确地描述拉伸全过程的应力应变关系。
