板式换热器板内两相流动分配特性分析及优化
2024-02-05魏文建徐国梁张志锋丁二刚王炎峰
魏文建 徐国梁 张志锋 丁二刚 王炎峰
(1 浙江水利水电学院 先进换热与能源应用研究所 杭州 310018;2 丹佛斯板式换热器有限公司 海盐 315012;3 浙江盾安热工科技有限公司 诸暨 311835)
板式换热器因结构紧凑和换热高效广泛用于制冷空调、石油化工等多个行业。近年随着压缩机单体能力的增加,板式换热器单体能力亦越来越大。板式换热器的大型化可通过增加板片数和增加单片面积两种方式实现。板片数的增加使板间分配不均,从而造成性能衰减。因而换热板单片面积的增加是实现板式换热器大型化的重要方式之一。但随着单片面积的增加,流体在通道内沿换热板表面均匀流动和分配变得困难,特别是气液两相流动情况。流体尤其是液体沿换热板表面分布不均,会影响换热板单片面积的有效利用,进而影响板式换热器的传热效率。
根据板式换热器应用和结构不同,现有文献对流体在板式换热器内分配特性的研究主要表现在两个方面:1)针对石化、区域供热等应用领域的可折式板式换热器[1]。可折板式换热器的工作介质通常为单相流体,多个板片通道之间的流体分配问题不严重。但由于其单片面积较大,存在板内分配问题[2-4],通常做法是在流体进入有效换热区之前设计独立的导流区。2)针对应用于制冷空调等领域以相变流体作为工作介质的钎焊式板式换热器。主要研究流体在通道间分配不均对性能的影响以及分配器的设计。W. Yoon等[5-8]对板式换热器制冷剂分配不匀对换热器和机组性能的影响进行了实验研究。W. Li 等[9-11]通过实验及可视化对两相制冷剂在板式换热器板孔内的流动型态进行了研究,并建立了相应的数学模型来定量描述两相流体在各通道间的分配情况。H. Shokouhmand等[12-13]研究了板片数的增加引起板间分配不匀对板式换热器性能的影响。Zhang Yun等[14]通过分析分配器参数对通道间分配均匀性的影响提出了分配器优化方案。有些学者对板式换热器换热和压降关联式进行了研究,并开发了板式换热器性能预测的两相模型[15-16],但未考虑分配不均的影响。笔者基于计算流体力学数值模拟方法,对板式换热器板间分配器在单相流动和两相流动时的分配性能分别进行了研究[17]。与上海交通大学丁国良教授团队合作对点波板式换热器和带有分配器的钎焊板式换热器内各支路的气液流量分配特性建立了预测模型,开发了适用于该模型的求解算法,解决了带分配器的板式换热器流道间气液两相流量分配的定量模拟问题[18-19]。
综上所述,现有文献都是对制冷用板式换热器板间分配不匀特性进行的研究。近年来,随着钎焊板式换热器的大型化,特别是兆瓦(MW)级产品的出现,单片面积可达0.5 m2及以上[20-21],制冷剂两相流体在通道内换热板表面的分配均匀性成为影响钎焊板式换热器传热效率的重要因素。由于钎焊板式换热器高承压和紧凑性要求,不允许如可折式板式换热器在进入换热区之前增加独立的导流区。因此,板片波纹结构的设计不仅要考虑换热单元的换热效果,更重要的是与板内分配特性相关联,从而增加了换热板设计的复杂性[22-24]。目前行业内板式换热器存在两种基本板型,即人字波板和点波板。点波板式换热器具有高强度和高效换热的优点[25-27]。由于结构不同,其板内流动分配特点与人字波板有所不同。
本文针对制冷用钎焊板式换热器板内分配均匀性问题及研究不足,通过计算流体力学建模分析方法采用两相状态R410A制冷剂作为介质,对两相流体在人字波板和点波板两种板片内的流动分配特性进行研究,为钎焊板式换热器设计开发人员提供理论依据。
1 物理数学模型建立
1.1 板片及流动单元物理模型
针对常规人字波板和点波板两种不同结构的板式换热器板片进行模拟,其中最大尺寸为600 mm ×100 mm,计算域大小为300 mm×100 mm,其中流体流动方向即长度方向为300 mm,流动法向方向为100 mm。由于仅考虑流动而忽略换热,故采用单流道流动计算模型。图1所示为人字波板和点波板的流动计算物理模型。图2所示为人字波板和点波板流动计算基本单元物理模型。人字波和点波板片结构参数如图3所示,波点大小为1.6 mm,波点排列为90°夹角,波点间距为5.6 mm。板片为材料厚度0.2 mm的不锈钢316L。人字波纹角度为120°,波槽深度为1.2 mm,波槽间距为7.2 mm,板片为材料厚度0.35 mm的不锈钢316L。

图1 板片物理模型
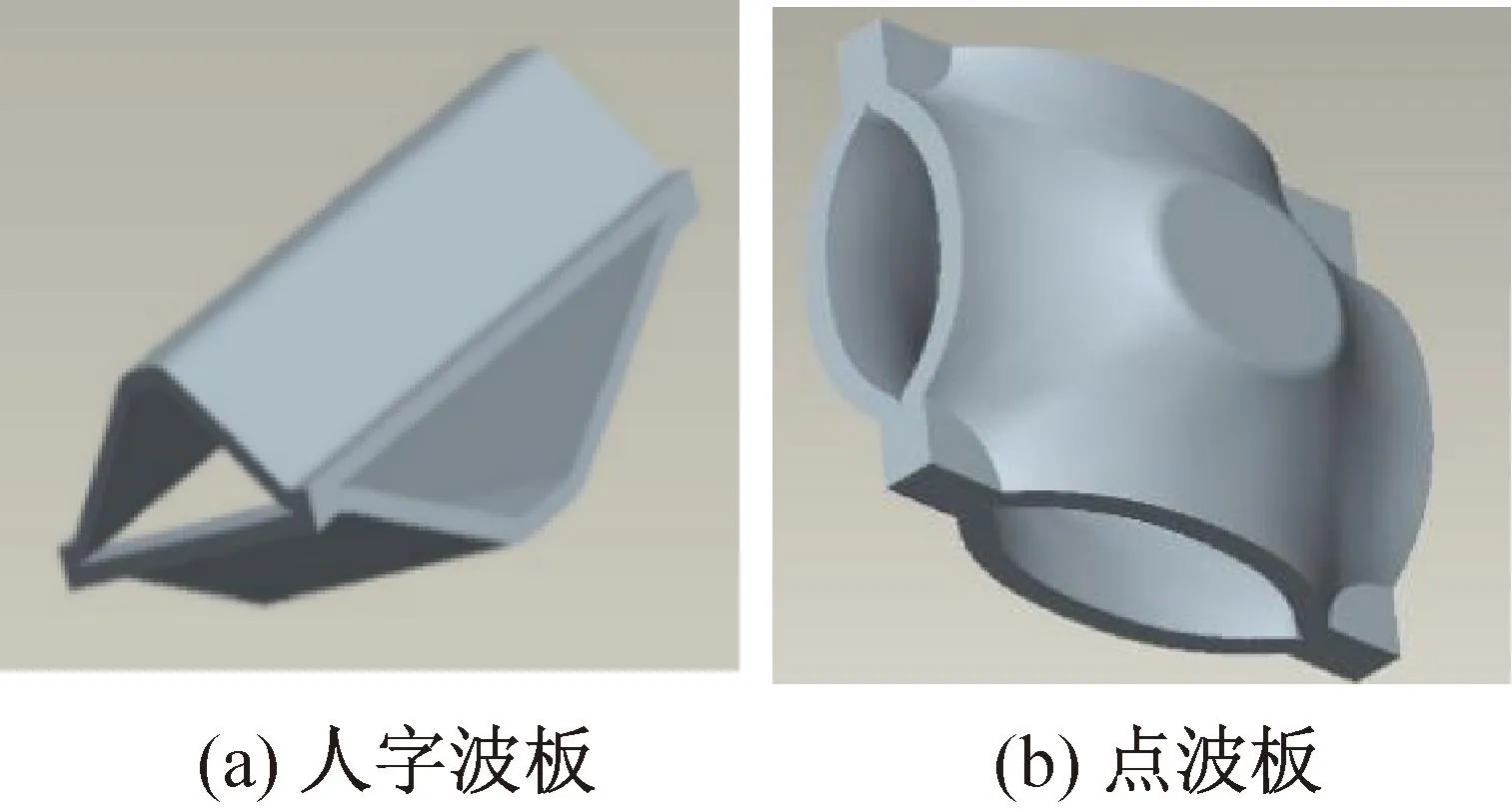
图2 板片流动基本单元物理模型
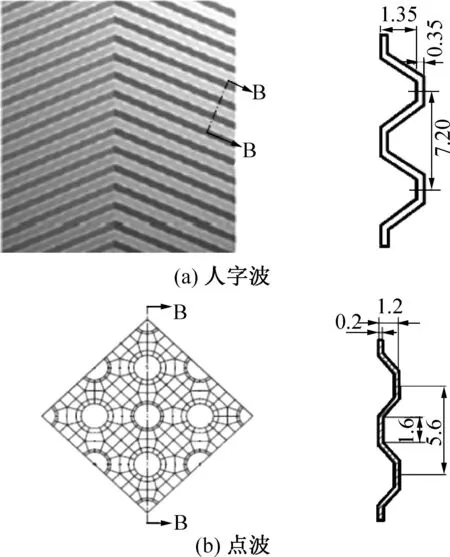
图3 板片结构参数
1.2 相关假设及数学模型
为研究流动分配情况,采用无换热条件下的气液两相状态R410A做为介质,且进行如下假设:
1)流体各物理量不随时间变化,为两相流体,定常流动;
2)工作流体为牛顿流体;
3)忽略由于密度差异引起的浮升力;
4)忽略流体流动时的黏性耗散作用所产生的热效应;
5)流动过程中无换热,忽略流体干度变化。
对于两相流体,因混合模型考虑了滑移速度且允许相间贯穿,对气液两相流体选用混合模型对其在板式换热器通道内的流动进行模拟计算,其控制方程如下。
连续性方程:
(1)
(2)
(3)

动量方程:
混合模型的动量方程通过对所有相各自的动量方程求和获得:
(4)
(5)
(6)
为了提高湍流计算的精度采用RNGk-ε模型,仅考虑流动且无传热面,各流体接触面视为绝热面,外部边界条件设为无滑移速度边界条件,单相流动流道进口采用速度入口条件,两相流动为质量流量入口条件,板片流道出口为流体压力出口条件。
1.3 建模分析流程及验证
图4所示为建模分析流程图。完成几何模型构建及网络独立性审查后,再通过对制冷剂气液两相边界条件的设定进行联立方程求解,直至求解器符合收敛判据。否则,需要调整设定条件重新计算。仿真模型压降计算结果与丹佛斯实验室测得的相同条件下水和R410A制冷剂在相近局部干度下的实验数据进行了对比,实验测试系统原理及不确定性分析参见文献[23,28]。对比结果如表1所示。其中水的仿真计算和测试工况为:进、出口水温分别为12 ℃和7 ℃,通道流速为0.5 m/s,对于单相水的计算结果偏差小于5%。R410A的测试工况为:阀前温度35 ℃,过冷度5 ℃,蒸发温度为4 ℃,换热器进口干度为0.4,出口干度为0.6,沿程干度变化控制在0.2,进出口平均干度为0.5,通道内气液两相平均流速为0.65 m/s,两种板型R410A两相压降的计算偏差均在12%以内。R410A两相计算结果与实测结果偏差略大主要是由于实际测试过程中存在流动换热,进出口平均干度和平均流速虽与仿真条件相同,但沿程干度变化约为0.2,而仿真计算中未考虑换热,即假定流动过程中干度不变。由表1可知,对于两种板型单相和两相仿真结果与实测数据一致性较好,其偏差在可接受范围内,说明压降仿真计算模型可靠。

表1 压降仿真计算结果与测试结果对比偏差

图4 建模分析流程图
1.4 网格划分
由于板式换热器模型结构较复杂,模型采用非结构四面体网络划分,整个流道由基本流动换热单元组成。图5所示为不同网格划分数目,发现当基本流动换热单元网格数目达28 936时,压降变化小于1.5%。综合计算精度和速度,本文采用28 936数目的基本单元网格划分密度。

图5 基本流动单元网格数目
2 模拟结果分析
2.1 评价参数
目前公开发表的文献中还鲜有提及板内气液两相分配不均性的描述及评价方法。为了定量评价板内分配均匀性,本文采用流动法线方向同一相对位置处的两相和液相质量分数与单一通道内两相和液相总质量分数的比值作为分布均匀性评价指标。当量段面质量流量分布如图6所示。量化两相和液相流动分配均匀性评价参数定义如下:mi,tp为流动法向当量段面处第i个截面的实际两相质量流量,kg/s;mi,liq为流动法向当量段面处第i个截面的液相质量流量,kg/s;N为当量段面处的划分截面数,N随板片宽度的增加而增大。当量段面的位置为流动方向上距离入口孔径中心的垂直高度与流体进出口孔径中心间距的比值,即h/H。

图6 当量段面截面质量流量分布
1) 平均两相流量:两相流动完全均匀分配时当量段面处单个截面的平均两相质量流量。
(7)
式中:mtot为板式换热器总质量流量,kg/s。
2) 平均液相流量:两相流动完全均匀分配时当量段面处单个截面的液相质量流量。
(8)
式中:xinlet为板式换热器进口干度。
3) 两相流量偏差:两相流动时当量段面处第i个截面实际两相流量与平均两相流量之间的相对偏差。
(9)
4) 液相流量偏差:两相流动中当量段面处第i个截面实际液相流量与平均液相流量之间的相对偏差。
(10)
5) 平均两相流量偏差:两相流动中板片当量段面处所有截面两相流量偏差的平均值,用于评价两相流体在板内当量段面处整体的均匀分配情况。
(11)
6) 平均液相流量偏差:两相流动中板片当量段面处所有截面液相流量偏差的平均值,用于评价液相流体在板内当量段面处整体的均匀分配情况。
(12)
2.2 人字波板板内流动分配
图7所示为人字波板式换热器板内流动分配模拟结果。由图7(a)可知,人字波板沿流体流动的法线方向,压力分布相对均匀,在人字波顶点处的压力略高而两侧略低。由图7(b)可知,气液两相先从沟槽向两侧流动,然后侧翻入下一沟槽。但气相要早于液相发生侧翻,可见在人字波顶点附近流速相对较大。图7(c)所示气相干度的的变化,对于给定的人字波板结构,板内气液相分配整体均匀性较好,反映液体侧向流动性较好。图8和图9所示为当量段面处液相体积分数、液相和两相流量偏差沿板片宽度方向的分布。靠近板中心位置液相体积分布略高于板片两侧。计算得到的平均液相流量偏差和平均两相流量偏差分别为15.6%和14.2%。
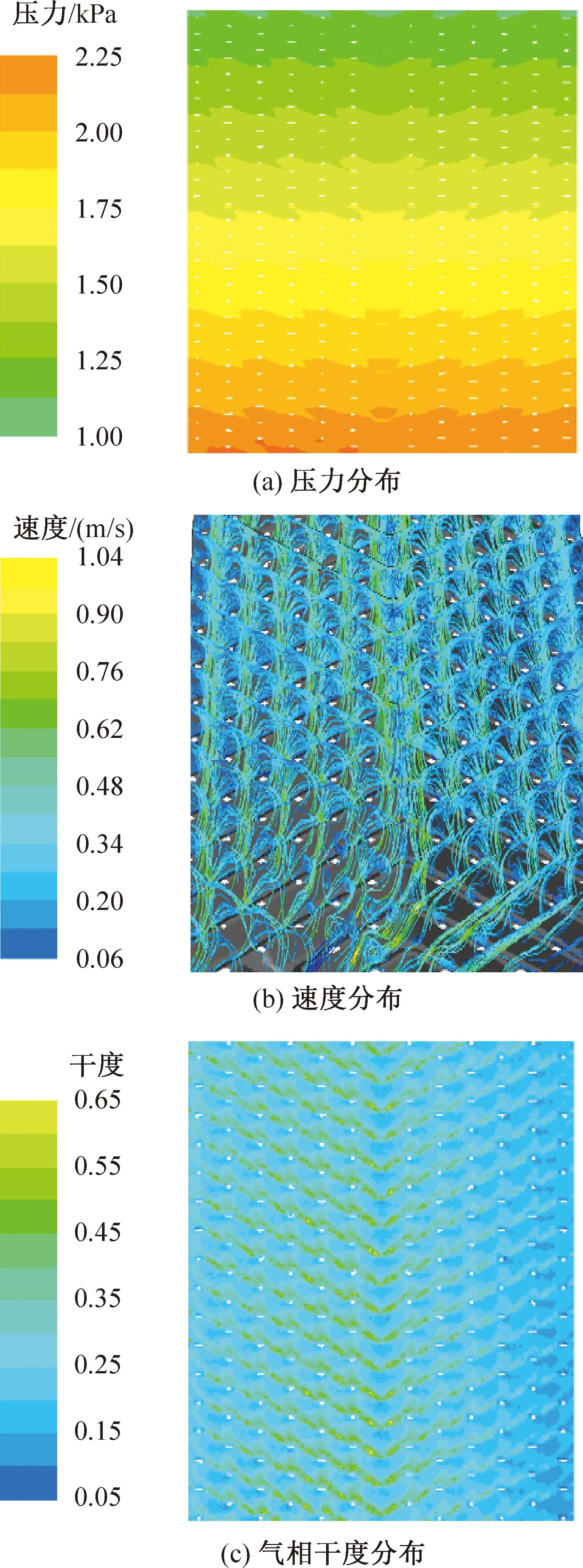
图7 人字波板模拟结果
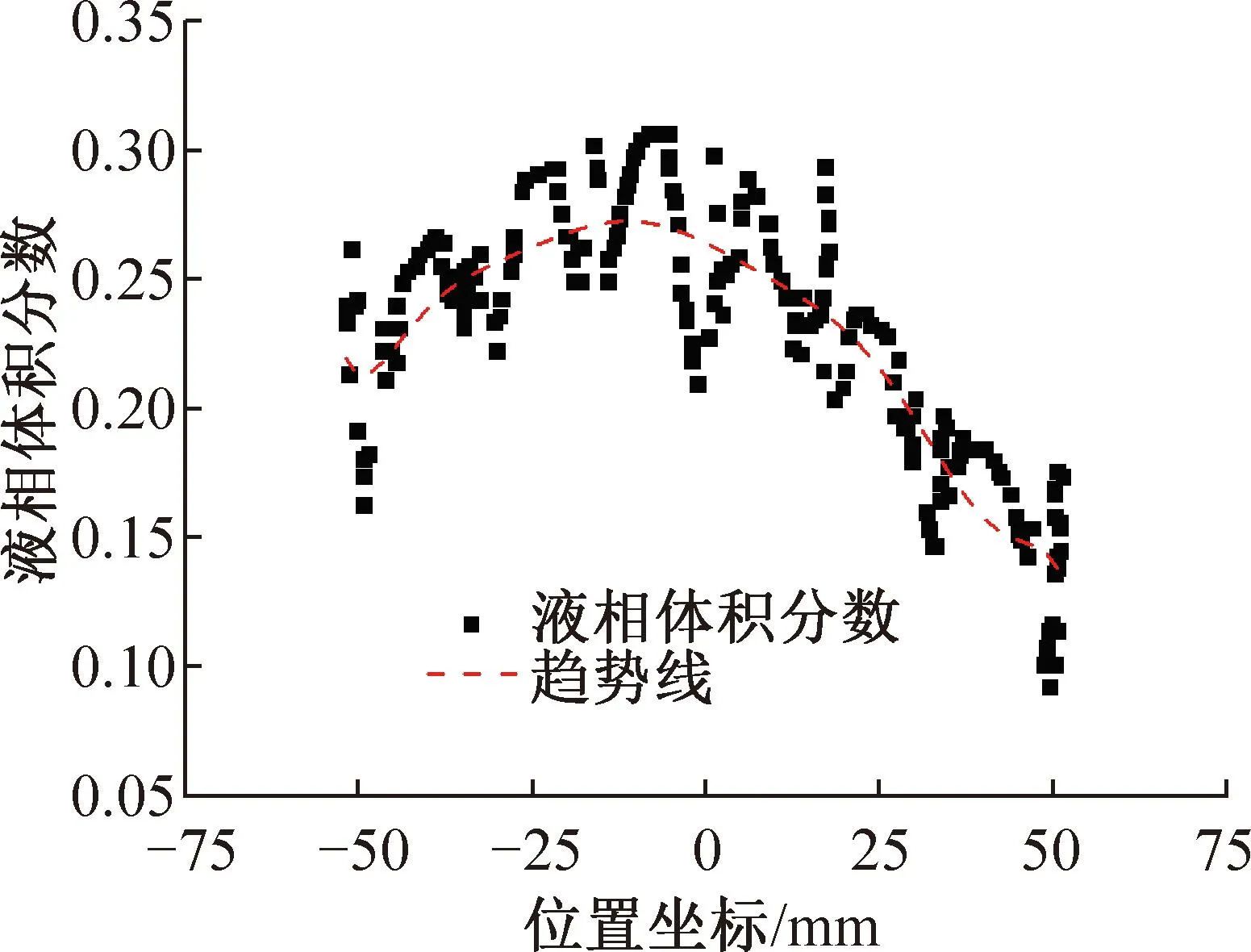
图8 人字波板当量断面液相体积分布
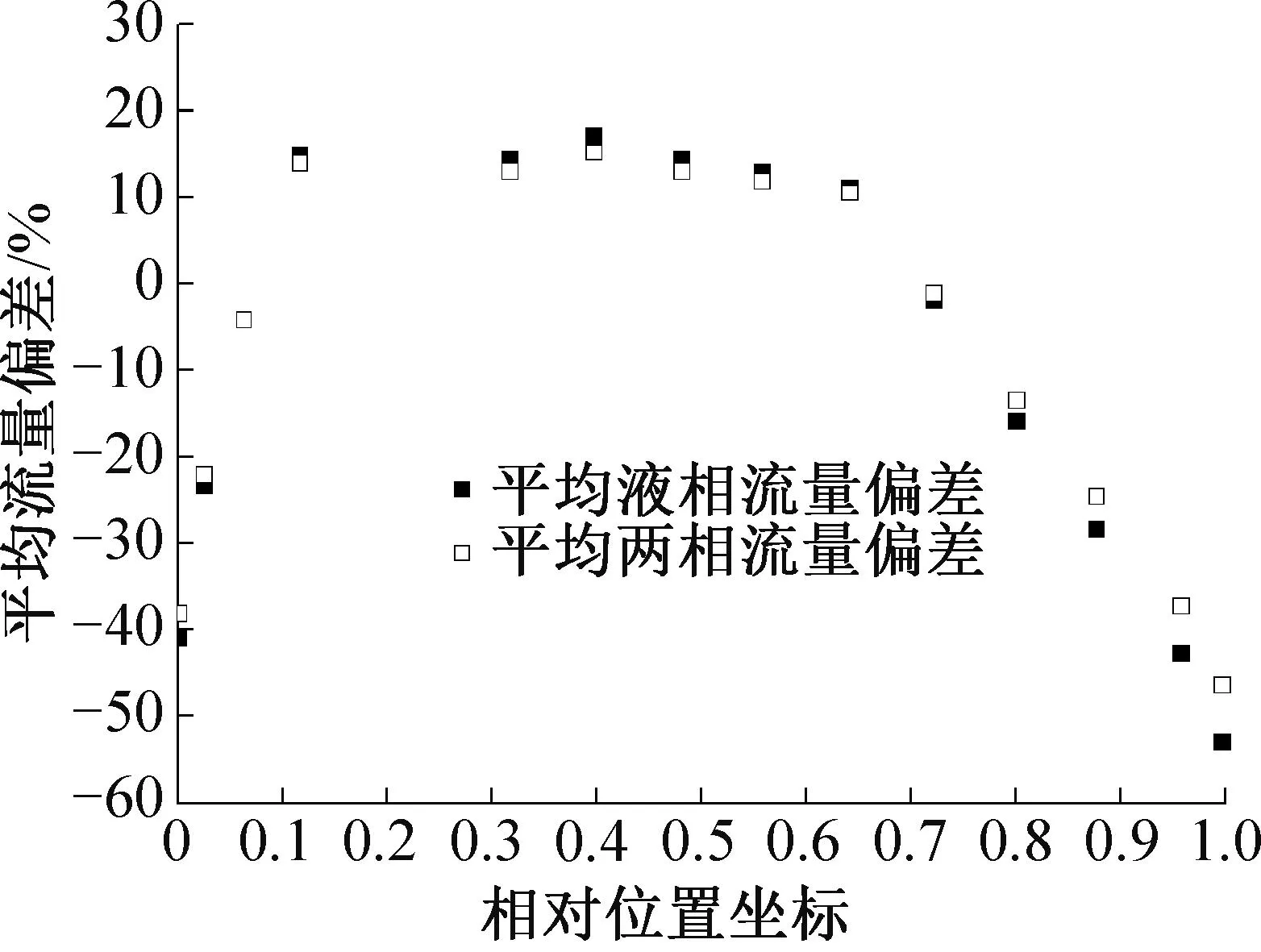
图9 人字波板平均液相和平均两相流量偏差分布
2.3 点波板板内流动分配
图10所示为气液两相在点波板板内流动速度分布。由图10可知,气体较易沿靠近入口的最短路径流动,制冷剂入口侧气体流速略高。表明近入口端气体质量流量高于远入口侧。点波板在当量断面的气相速度分布和液相体积分数分布如图11所示。由图11(a)可知,流体进出口近侧的气相流速明显高于远端,与图11(b)所示液相体积分数的分布一致。图12所示为不考虑换热,仅考虑气液两相制冷剂不同时刻的气液两相流动时热图,左下侧为制冷剂入口,左上侧为制冷剂出口,在制冷剂流动的法线方向上,制冷剂液体的分布不均显著,靠近制冷剂进口侧气体多于液体。由此可知,仿真结果与流动热图趋势性一致。液态制冷剂不能均匀分布于换热板片表面,从而降低换热板有效传热面积,造成性能下降。根据当量断面处流速和体积分数,计算得到的平均液相偏差和平均两相偏差分别为41.3%和39.6%。
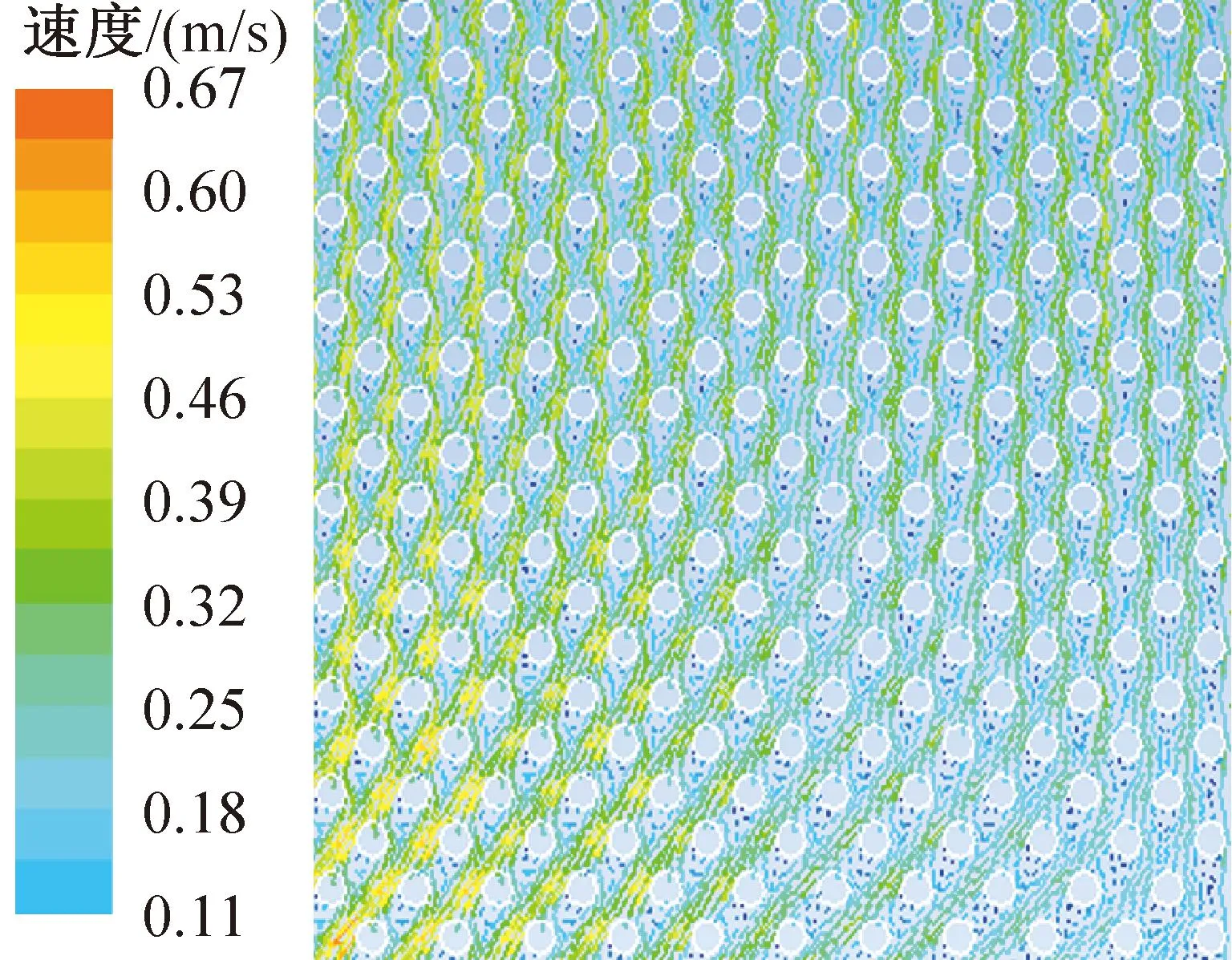
图10 点波板流速分布
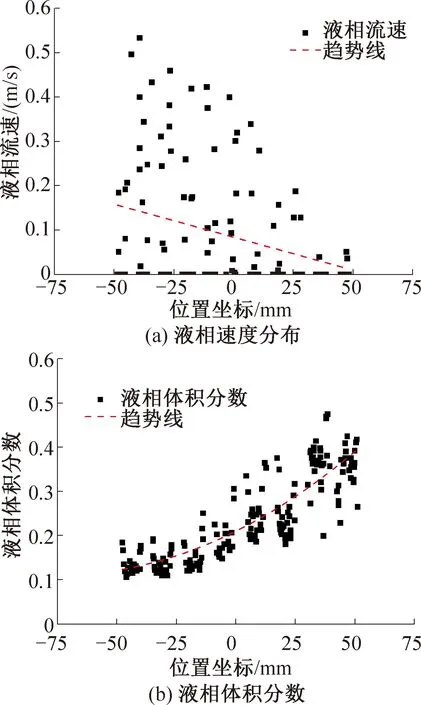
图11 点波板当量断面气相速度和液相体积分数分布

图12 点波板两相制冷剂流动热成像
3 点波板板内流动分配优化
由点波板流动分布的结果可知圆型点波板在流体流动方向上存在直通断面,从而形成气体短路通道,过早发生气液两相分离现象,致使出现近出入口端气体过多,而远端液体偏多的板片表面流体分布不均问题。如何减小直通断面大小以及如何驱动流体侧向流动成为解决问题的关键,为此笔者提出了一种新型仿生“鱼鳞”点波板片结构并针对表2所示的结构参数对其进行数值模拟,模拟结果如图13所示。由图13(a)可知,压力分布沿板宽方向较为一致。由图13(b)可知,虽然仍有部分气体均匀通过直通断面,流体侧向断面流动增大,流速沿板宽分布相对较为一致。表明“鱼鳞”点波可以有效减小流体方向上的直通断面大小,其下凹弧形结构可以增强流动方向的湍流,并产生二次涡流,延迟气液两相分离。另一方面,在减小直通断面的同时增加侧向流通截面,降低侧向阻力驱动液体侧向流动。图14所示为“鱼鳞”点波结构的流线型态,二次涡的形成和侧向流动清晰可见。图15所示为“鱼鳞”板片反映液相分布的红外图像,可见该新型点波结构可以有效驱动液相侧向流动,气体在中心部位稍多,从分布看与“鱼鳞”点波排列角度基本一致。采用相同方法计算得到当量断面处的平均液相流量偏差和平均两相流量偏差分别为8.9%和7.6%。板片表面流体流动和分配的不均匀性改善显著。

表2 鱼鳞式点波结构参数
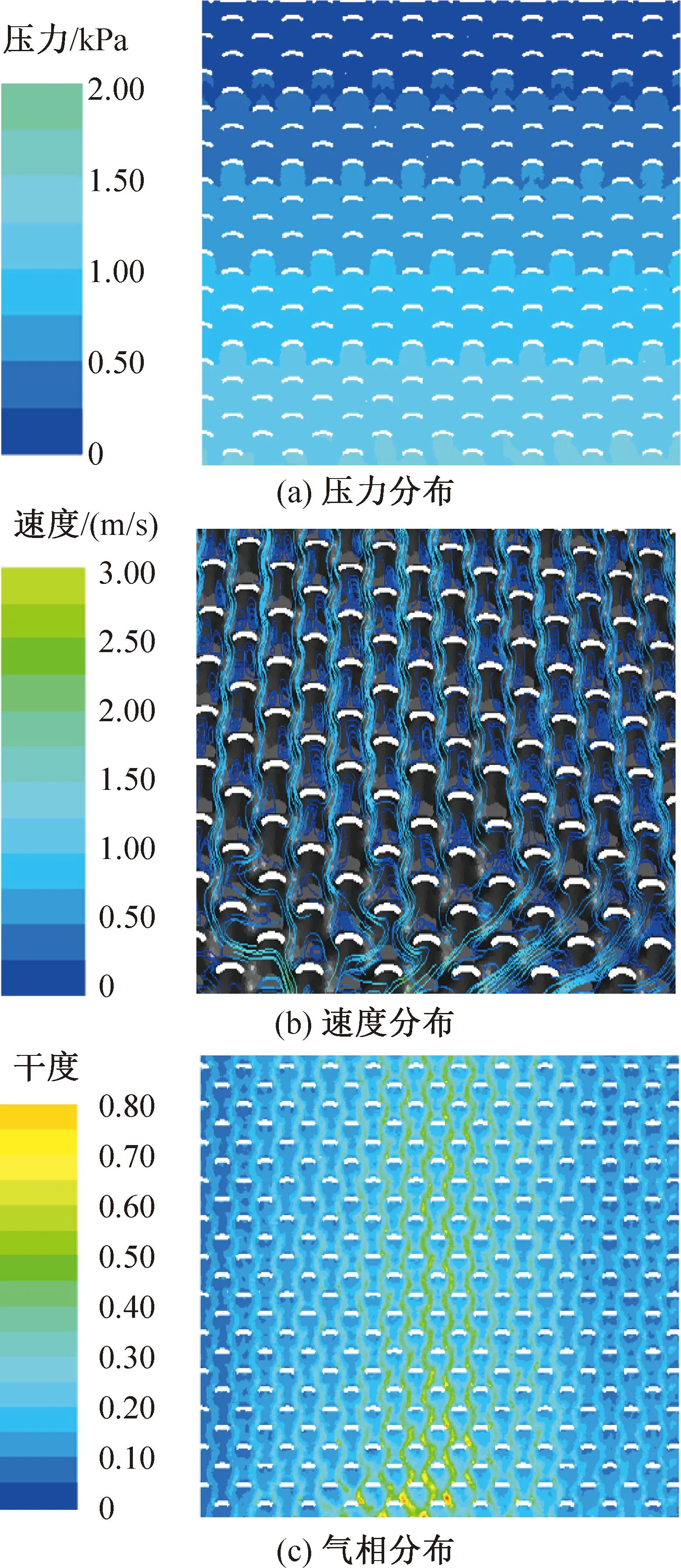
图13 “鱼鳞”点波板模拟结果

图14 “鱼鳞”点波板的流线型态

图15 “鱼鳞”点波板两相制冷剂流动热成像
4 结论
本文采用人字波板和点波板两种换热板片进行计算流体力学数学建模研究板内流动分配特性,提出了一种板内分配均匀性评价方法,通过实验数据对仿真模型进行了验证,得到如下结论:
1)采用的仿真模型和计算方法可靠,对于相同结构参数和工况条件,单相和两相压降计算结果与实验数据偏差分别在5%和12%以内。
2)人字波板相对同宽度点波板,气液两相侧向流动分配相对较好,但仍呈现一定程度侧向分布的不均匀性,平均液相流量偏差和平均两相流量偏差分别为15.6%和14.2%。
3)点波板气液两相侧向流动受限,因直通截面存在使气体易出现“短路”现象。平均液相流量偏差和平均两相流量偏差分别为41.3%和39.6%。影响板内分配均匀性的主要因素是直通断面大小、相分离和侧向流动驱动力大小。
4)降低直通断面并产生二次涡的“鱼鳞”点波结构可有效改善板内分配,平均液相流量偏差和平均两相流量偏差分别为8.9%和7.6%。表明点波板通过优化设计,可以实现与人字波板相同或略优的侧向流动效果,以满足板内均匀分配和性能提升要求。
本文受浙江省“尖兵”“领雁”重大研发攻关计划项目(2022C01159)资助。(The project was supported by the "Pioneer" and "Leading Goose" R&D Program of Zhejiang (No. 2022C01159).)
