凹非球面的非零位干涉检测技术

张 旭，李世杰，刘丙才，田爱玲，梁海锋，蔡长龙

（西安工业大学 光电工程学院,陕西 西安 710021）

1 引言

非球面光学元件可以更好地校正像差、改善像质，提供出色的成像锐度和更高的分辨率，同时还能大大减少光学系统的镜片数量、重量与尺寸[1]，已经越来越多地应用于军事国防及高科技民用技术等领域[1-3]。在非球面制造过程中，高精度检测手段可为加工过程提供准确的面形误差分布，指导加工，为获得高精度的非球面光学元件提供保障[4]。

常用的非球面检测技术有轮廓检测法、计算全息法与子孔径拼接检测法等。其中，非接触式探针的轮廓测量法[5]可实现对凹、凸非球面的测量。其测量精度可达到亚微米级。但轮廓检验法精度受限、效率较低，适用于元件研磨期的精度检测[6-7]。计算全息法可实现深度非球面的测量，但该方法中CGH（Computer Generated Hologram）与待测非球面之间是一一对应的关系，不具备通用性，且CGH 加工成本较高。非零位子孔径拼接技术可实现对大口径、深度非球面反射镜的测量，检测结果精度较高。但该方法的测量时间长，对机械结构要求高且数据处理复杂[8-9]，拼接算法误差更会直接影响检测精度。

此前，王孝坤[10]提出了一种非球面的非零位检测方法。该方法中未给出回程误差的具体计算方法，且调整误差只分析了活塞误差（Piston）、倾斜误差（Tilt）和离焦误差（Power）的影响，而忽略了由于光路调整距离变化而引入的球差。师途[14]在其文章中列出了3 种回程误差的计算和去除方法，并对3 种方法去除回程误差后的面形结果做了比较。但文中没有具体的计算与处理方法，也未考虑检测中产生的调整误差。在本文中，不仅给出了回程误差的理论模型和计算方法，还详细分析了调整误差引入的原因及计算去除方法。

针对抛光阶段凹非球面的快速与通用化检测需要，本文提出了将其当做球面直接用干涉仪的球面标准镜头进行检测，再对由非球面度引起的回程误差进行数据处理的非零位干涉法。文中结合实际检测情况对非零位检测中引入的误差进行了原理分析，对其中的回程误差进行建模计算及仿真，并仿真分析了回程误差与光轴方向距离引起的误差分离，验证了回程误差的固有性。分析了调整误差与初级像差的关系，并进行了仿真与实验验证。最后，用该方法实验检测了两个口径为90 mm，顶点曲率半径分别为606 mm、348 mm的不同非球面度的凹非球面，并用零位干涉法或LUPHOScan 光学轮廓检测法的结果进行了对比，验证了检测结果的可靠性。

2 检测原理与方法

2.1 非零位干涉检测原理

将非球面当做球面直接用干涉仪的球面标准镜头可完成非零位检测[10-12]，如图1 所示。由干涉仪发出的光线在焦点汇聚后产生球面波前，由于非球面度的存在会引入回程误差[12-14]，偏离了零位检测的路径，导致入射到非球面表面的参考光束不能原路返回，而是在球面标准镜头的焦平面处形成弥散斑。考虑到实际检测过程中，很难通过调整干涉仪与被测非球面之间的距离使参考球面波的焦点与待测非球面最接近参考球面的球心重合[10]，将会产生调整误差[15]。所以，用非零位法直接干涉检测的结果Edet(x,y)除了含有非球面的自身面形误差Easp(x,y)、由非球面度引起的回程误差Eret(x,y)，还存在调整误差Eadj(x,y)，即

图1 非零位干涉法直接检测非球面原理示意图Fig.1 Schematic diagram of aspheric surface directly tested by non-null interferometry

因此，要获得被测非球面的面形误差Easp(x,y)，需要将非零位干涉检测时产生的回程误差Eret(x,y)与调整误差Eadj(x,y)进行去除。

2.2 回程误差的建模与计算

在非零位检测中，回程误差来源于待测非球面的非球面度，即非球面与其最接近的参考球面沿后者法向的偏离量[16]。将待测非球面视为表面无缺陷的理想面形，建立非零位检测光线追迹模型，如图2 所示。以非球面上的任一点B(x,y,z)为例进行光线追迹，点A为干涉仪标准镜头的会聚焦点，AB为入射光线，BC为反射光线，OA为待测非球面的最接近球面的曲率半径（其值为L）。由非球面度引起的误差反映到测量光路中具体表现为：入射到非球面的检测光线与经非球面表面反射的光线之间的偏差，将两者的差值称为光程差OPD（Optical Path Difference）。

图2 非零位检测光线追迹模型Fig.2 Ray-tracing model of non-null test

采用空间光线追迹方法计算 OPD[17]。其中：a为入射光的单位方向矢量，b为反射光的单位方向矢量，d为待测非球面B点处的单位法线矢量。入射光线的模长 |AB|可根据检测光路的具体参数及待测非球面方程直接求出，而反射光线的模长|BC|则要结合反射定律的空间矢量解析式[17]求出b的各单位方向矢量，即

设C的坐标为C(x0,y0,-L)，通过建立直线BC的方程可求出 |BC|，即有

式中：C0为待测非球面的顶点曲率。

通过分析非球面度引起的误差知，OPD(x,y)中除了包含Eret(x,y)外，还存在由实际的待测非球面与其最接近参考球面在曲率半径方向的偏离引起的误差。该误差包含两部分，第一部分为实际检测时，OA不准确等于L时产生的离焦误差EOPD(Power)(x,y)，第二部分为不同OA值时与L的偏离量 ΔL所引起的球差。将 ΔL所引起的误差记为△OPD(x,y)，其表达计算式如（4）式所示，则其球差可表示为EΔOPD(Sphere)(x,y)，则有

2.3 调整误差的分离与去除

搭建实际检测光路过程中，只能尽可能地调节使待测非球面无限接近理想位置，而非精确处于理想位置，因此，将引入调整误差Eadj(x,y)。由于该检测系统只有两个部件，故两者的调整误差只可能包括两者之间的距离误差和倾斜/偏心误差[14]，如图3 所示。

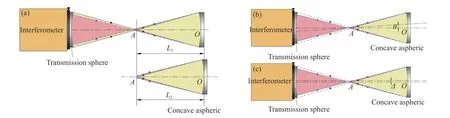
图3 调整误差引入的像差。（a）距离引起的离焦；（b）光轴倾斜引起的倾斜误差；（c）偏心引起的彗差Fig.3 Aberration caused by adjustment errors.(a) Distance induced defocusing;(b) tilt error caused by optical axis tilt;(c) coma caused by optical axis offset error

根据像差理论，当存在距离误差时，会在检测结果中引入离焦误差EPower(x,y)；当存在倾斜/偏心误差时，会引入倾斜和彗差，检测时倾斜像差一般会去掉，故由倾斜/偏心引入的像差最终仅表现为彗差EComa(x,y)，即

由于 Zernike 多项式各项的基函数与光学检测中观测到的像差的表现形式是一致的，所以光学分析中常将光学像差的波阵面形态分解为Zernike 多项式的组合[18]，且如表1 所示。

表1 Zernike 多项式的项数与像差的对应关系Tab.1 Correspondence between the terms of Zernike polynomials and aberrations

如表1 所示：Zernike 多项式的Z4项对应离焦误差（Power）项；Z7、Z8项分别对应X方向的彗差（Coma X）和Y方向的彗差（Coma Y）；Z9项对应初级球差（Primary Spherical）项。因此，文中采用Fringe Zernike 多项式[18-20]在笛卡尔坐标系中对Edet(x,y)进行36 项拟合，再根据其项数与像差的关系减去含有Eadj(x,y)的项。在Zernike 多项式拟合面形的条件下，有：

最后，将式（5）与式（7）代入式（1）中，得

通过式（8），可计算得到被测非球面的面形误差Easp(x,y)。

3 回程误差仿真计算

3.1 非零位法检测凹非球面

将不同参数的待测凹非球面带入Zemax 进行建模，可对非零位检测的干涉条纹进行仿真分析。经分析发现，干涉条纹的疏密程度随非球面度的增大而变密。当非球面度≤5 μm 时，产生的干涉条纹可分辨解析。若继续增大非球面度，干涉条纹将变得过于密集而无法解析。经判断知，该方法可实现对非球面度小于5 μm 的非球面的非零位检测。

下面以两个在该范围内的不同非球面度的凹非球面作为实验件，对文中提出的非零位检测方法进行仿真计算与实验检测，其具体参数分别如表2、表3 所示。

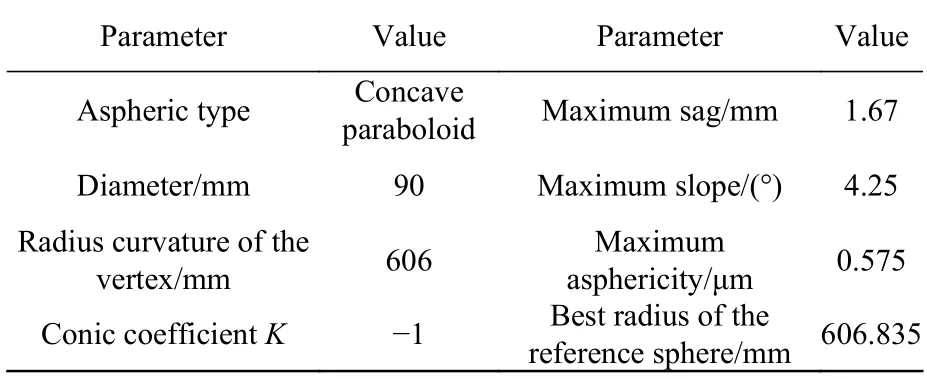
表2 凹抛物面参数Tab.2 Parameters of concave paraboloid surface

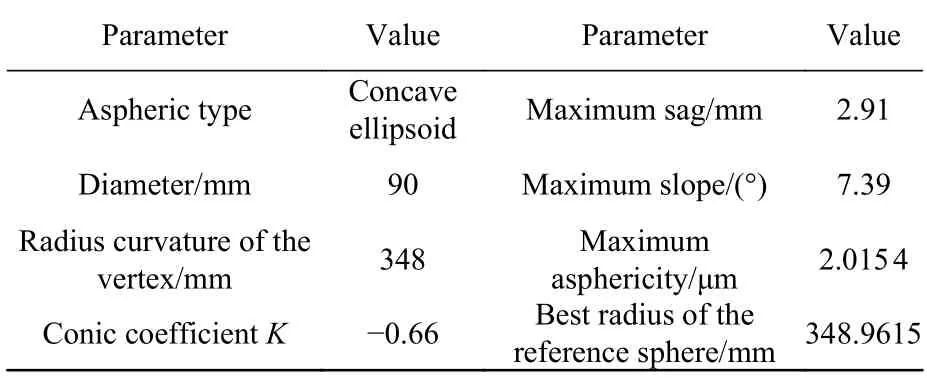
表3 凹椭球面参数Tab.3 Parameters of concave ellipsoid surface

3.2 回程误差的仿真及与离焦误差的分离验证

通过前面的分析可知，要得到Eret(x,y)，需要将OPD(x,y) 中含有的离焦误差EOPD(Power)(x,y) 与ΔL所引起的球差EΔOPD(Sphere)(x,y)去除。去除思路是先根据抛物面的参数，建立非零位光线追迹模型，结合MATLAB 编程仿真计算出OPD(x,y) 与ΔOPD(x,y)，并将其分别拟合为36 项Zernike 多项式的形式，再用OPD(x,y) 减去EOPD(Power)(x,y)（OPD(x,y)拟合后的第4 项）与EΔOPD(Sphere)(x,y)（ΔOPD(x,y)拟合后的第9 项）。利用Zernike 多项式拟合后的精度可得到有效保证[21]。下面以两个凹非球面为例，根据EOPD(Power)(x,y)和EΔOPD(Sphere)(x,y)的特点设计与Eret(x,y) 的分离实验，即赋予 OA5 组不同的值，观察最终所得到的Eret(x,y)，如表4、表5所示。

表4 凹抛物面回程误差的仿真计算结果Tab.4 Simulation calculation results of retrace error of concave paraboloid surface

表5 凹椭球面回程误差的仿真计算结果Tab.5 Simulation calculation results of retrace error of concave ellipsoid surface

从表4、表5 可知，在OA值不同时仿真计算得到的OPD(x,y) 值相差很大，但去除EOPD(Power)(x,y)与EΔOPD(Sphere)(x,y) 后，计算得到的Eret(x,y)值相差在亚纳米量级。由此可知Eret(x,y)是非球面固有的，其只与非球面的表面形状参数有关，OPD(x,y)中含有的EOPD(Power)(x,y)与EΔOPD(Sphere)(x,y)可直接去除。

4 检测实验与对比

4.1 凹非球面非零位干涉检测实验

根据表2、表3 设定的凹非球面参数，采用Zygo 激光干涉仪，选用F/3.3 的球面标准镜头，对其进行非零位检测。检测过程中，尽量调节图2 中OA的距离，使其与非球面的最接近球面半径接近。经过精密调节，获得非零位直接检测的结果，检测现场及结果如图4（彩图见期刊电子版）所示。

图4 非零位检测凹非球面时（a）实验装置及非零位直接检测（b）凹抛物面和（c）凹椭球面的数据Fig.4 (a) The experiment setup of non-null test for concave aspheric;data of (b) concave paraboloid surface and (c) concave ellipsoid surface obtained by non-null direct interferometry

由于该检测光路中难以对距离、倾斜/偏心误差进行精密监控，所以容易引入像差。下面结合2.3 节的调整误差分离与去除方法，以凹抛物面为例，对实验过程中的调整误差进行验证。

4.2 在非零位检测结果中去除调整误差

前面对实际检测中产生的Eadj(x,y)进行了原理上的分析，但因检测实验具有一定的随机性，本文以待测抛物面为例，在非零位检测光路中以Eadj(x,y)调节至最小时的数据与引入不同形态后的Epower(x,y)与EComa(x,y)去除前后的结果做对比，如表6、表7 所示。从表6 可看出，调节距离误差引入的EPower(x,y)对检测的干涉条纹与面形有较大的影响，利用2.3 节的去除方法可去除因距离误差引入的离焦误差对检测的影响。

表6 实验中距离误差引入的离焦误差与去除Tab.6 Defocusing error introduced by distance errors in experiments and its removal (nm)

表7 实验中光轴倾斜/偏心误差引入的彗差与去除Tab.7 Comet error introduced by optical axis tilt/offset error in experiment and its removal (nm)

在表7 中可看出，调节偏心/倾斜误差引入的EComa(x,y)对干涉条纹与面形产生的影响较小，利用2.3 节的去除方法可去除因偏心/倾斜误差引入的彗差对检测的影响。

通过上述分析可知，2.3 节的去除方法对实验中可能引入的EPower(x,y)与EComa(x,y)均表现出了较好的去除效果，即可有效去除实验中的调节误差Eadj(x,y)对检测结果的影响，不会对测量结果产生明显的影响。

将用非零位检测方法得到的检测结果Edet(x,y)(如图4（b）、4（c）所示)，分别读入到MATLAB 中进行数据处理。首先，采用2.3 节的方法去除调节误差Eadj(x,y)，然后，再去除回程误差Eret(x,y)(如表3、表4 所示)，最终即可得到两非球面的面形检测结果，如图5（a）、5（b）所示（彩图见期刊电子版）。

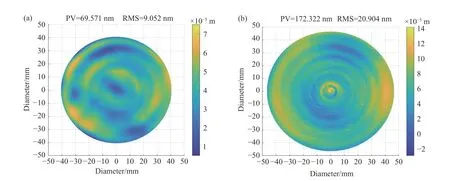
图5 非零位检测去除调整误差与回程误差。（a）凹抛物面处理后的面形结果；（b）凹椭球面处理后的面形结果；Fig.5 Non-null test results after removing adjustment error and retrace error.(a)Test results of concave parabolic surface;(b) test results of concave ellipsoid surface

4.3 检测结果对比与分析

文中用平面镜自准直法与LUPHOScan 轮廓测量法的测量结果作为对比来验证所提方法的检测准确性。图6（a）、6（b）（彩图见期刊电子版）为平面镜自准直法检测凹抛物面的光路图与检测结果，图6（c）（彩图见期刊电子版）LUPHOScan 轮廓仪测量的凹椭球面结果。

图6 凹非球面的对比实验。(a)平面自准直法检测光路图；(b) 自准直法检测凹抛物面的数据；(c) LUPHOScan 轮廓仪测量凹椭球面的数据Fig.6 Comparative experiment on concave aspheric.(a) The optical path diagram of plane autocollimation;(b) testing of concave paraboloid surface by autocollimation;(c) testing of concave ellipsoid surface using LUPHOScan

将两个不同非球面度的非球面非零位干涉处理得到的面形结果分别与其对应的验证实验进行对比，即图5（a）与图6（b）、图5（b）与图6（c）分别进行比对，可明显看出各组数据的面型分布一致，评价参数PV 与RMS 值都非常接近。上述结果表明非零位检测处理方法的准确性。

5 结论

针对抛光阶段凹非球面的快速与通用化检测需要，提出了利用Zygo 干涉仪的球面标准镜头直接对其进行非零位干涉检测的方法。分析了回程误差与调整误差的产生原理，并给出了校正原理与仿真实验验证。通过对两个具有不同非球面度的凹非球面进行非零位检测实验。其检测结果与自准直零位干涉检测法及LUPHOScan 轮廓测量法的测量结果均具有高度一致性，验证了本文所提方法的可靠性。由于干涉仪具有多种参数的标准镜头，故在不需要额外补偿元件的条件下能够匹配不同参数的凹非球面，实现其面形高精度测量，使该方法具有广泛的应用前景。