基于Pareto控制的多目标PSO算法在铣削参数优化中的应用

2024-02-05刘海妹

重庆理工大学学报(自然科学) 2024年1期

王奇,陈曦,刘海妹,赵彻,徐波

(1.常州工学院航空与机械工程学院, 江苏常州 213032;2.上海交通大学机械系统与振动国家重点实验室, 上海 200240)

0 引言

工艺参数是加工过程中的可控变量,影响关键零部件的加工质量和效率。高效的加工需要优化的加工参数,而低成本的加工需要延长刀具寿命。影响加工质量的关键因素之一为切削力。切削力模型广泛应用于工业和研究领域[1-2],其中分析模型[3-4]和有限元模型[5-6]得到了广泛应用。他们的共同点是校准切削力系数从而预测切削力[7-8]。例如,Kao等[9]基于切削力辨识的思想研究了环形刀具切削力系数的识别。Wang等[10]通过测量模态参数求解运动微分方程,并将实时振动的影响引入切削力模型。Wojciechowski[11]对斜铣削工况下球头铣刀切削力系数的识别方法进行了研究。

切削参数优化是控制加工过程、提高加工质量的重要方法[12-13]。随着加工时间的延长,刀具磨损不可避免[14]。因此控制刀具磨损、延长刀具寿命是参数优化的重要手段。Chen等[15]建立了一个考虑刀具磨损的切削力预测模型。Agrawal等[16]研究了加工环境对刀具侧面和凹坑磨损的影响,并将其与湿式切削进行了比较,发现低温切削可以延长刀具寿命。Bordin等[17]对刀具涂层和切削条件对刀具磨损的影响进行了研究。Wang等[18]通过在线测量递归更新了基于物理磨损率的刀具预测模型,解决了刀具磨损过程的不确定性。为了实现实时数据处理,Come等[19]利用人工智能系统集成的主轴数据进行刀具磨损的实时检测和控制。在获得足够数量的切削图像数据集后,García-Ordás等[20]提出了一种图像处理方法来描述和预测刀具磨损状态。

随着信息的发展和采集设备的更新,切削数据的数据量也在增加。许多学者提出了基于大数据挖掘的刀具寿命分析和预测方法[21]。Mikoajczyk等[22]提出了将人工神经网络应用于刀具图像的数据处理,以达到分析刀具磨损率的目的。Aghazadeh等[23]提出利用卷积神经网络和小波包提取加工过程的刀具磨损信息。Chen等[24]提出了一种利用深度置信网络预测刀具侧面磨损的深度学习方法。

目前,在切削参数优化的研究中,测试校准方法已经相对成熟,可以取得更好的效果,但测试量大,耗时长,推广使用难度大。因此,有必要借助人工智能算法快速准确地获得满足不同需求的最优参数组合。本文中基于切削力、刀具磨损和切削参数之间的映射关系,提出了一种PSO多目标切削参数优化方法,以提高加工效率。

1 问题描述和优化策略

本节将针对不同目的设定不同的优化目标,并进行切削参数优化,以实现切削数据的合理利用和数据挖掘。

1.1 优化目标与约束条件

铣削加工过程即为材料去除过程,为了提高加工效率,选取材料去除率作为优化目标。材料去除率(MRR)可以表示为:

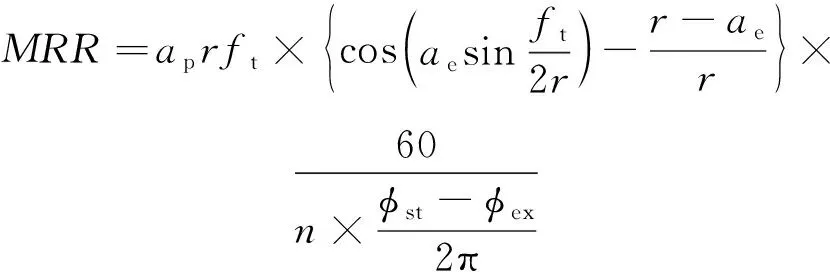
(1)

式中:ap为轴向切削深度;ae为径向切削深度;ft为每齿进给;n为主轴转速;r为刀具半径;φst、φex分别为切入角、切出角。

在连续加工过程中每当刀具磨损量达到一定阈值时需要进行换刀。加工参数对刀具寿命起到决定性的影响,因此选取刀具寿命为优化目标。在铣削加工中,刀具寿命即刀具铣削长度,是与机床转速和进给速度相关的函数,可以表示为:

L=f(n,ft)

(2)

式中:L为刀具切削长度。

实际加工中,为了使刀具寿命尽可能更大,选择最大切削长度作为优化的目标函数。随着加工的不断推进,刀具在切削热和应力的循环作用下,刀具磨损不断加剧,此时必然引起切削力的增大。而切削力增大会引起机床功耗增加,因此将切削力作为优化目标是必要的。切削力随刀具切入切出不断波动,选择刀具所受平均力的合力最小作为优化目标,平均力与合力可以分别表示为:

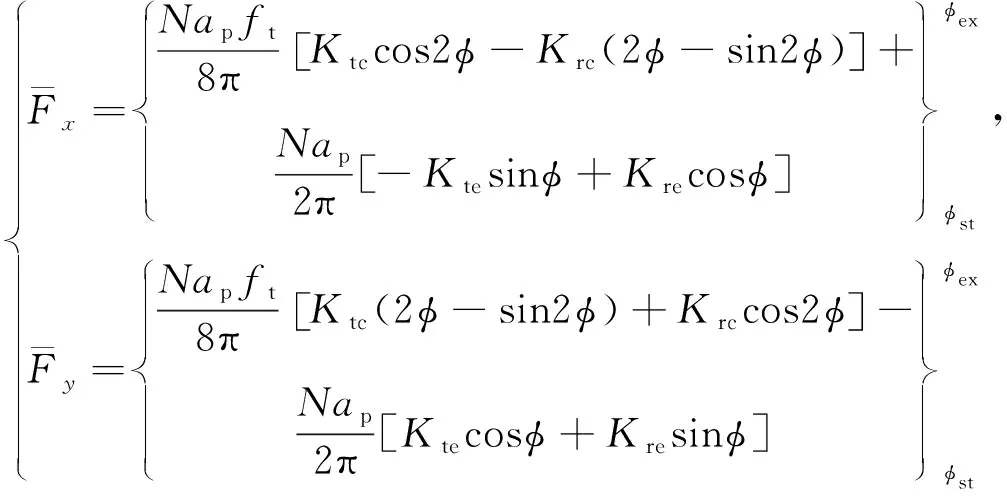
(3)

在铣削加工中的约束条件主要有:机床加工性能约束、切削参数约束和刀具刚度约束。

1.2 优化问题的数学模型

本文中的优化问题属于约束优化,其数学模型可以表示为:

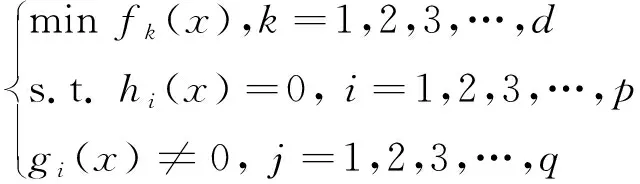
(4)

式中:x为问题的解;fk(x)为目标函数;hi(x)为等式约束;gi(x)为不等式约束。

目标函数可以表示为:

min[-L=-f(n,f)]

(6)

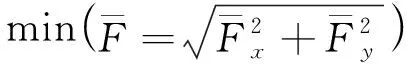
(7)

约束条件可以表示为:

(8)

式中:nmin、nmax为主轴转速范围;ft,min、ft,max为每齿进给范围;ae,min、ae,max为径向切深范围;Fmax为刀具承受的最大切削力;VBmax为设定刀具磨损最大值。

为了将各因素的影响引入到工艺参数优化模型中,在进行全局优化的参数选取时,设定主轴转速、轴向切深和每齿进给为优化变量。最终优化问题的解是由控制变量组成的工艺参数序列,可以表示为:

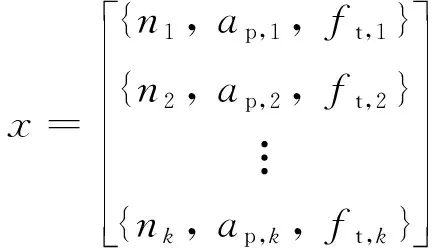
(9)

式中:k为参数区间离散间隔。

1.3 求解方法

多目标优化是现在许多工程与应用研究中需要解决的关键问题之一。由于优化目标维度的增加以及多个目标之间的相互牵制作用,多目标优化成为当下的难点与热点问题。粒子群算法构造简单,易于操作,所以被大家广泛应用,但是缺点是容易陷入局部最优解,而无法实现全局最优。而高维空间中Pareto支配规则可以用来比较个体间的优劣关系,所以本文中采用基于Pareto支配的多目标粒子群优化算法求解最优切削参数。结合数学模型和基于Pareto的多目标粒子群算法,本文中的优化问题可以按照以下步骤求解:

1) 数据关系模型,利用加工数据,建立切削力预测模型,以及材料去除率、切削长度与切削参数的关系,并以此为依据计算不同个体的关联度。

2) 参数初始化,设置种群规模Popt={X1,X2,…,Xm},最大迭代次数Nomax,个体粒子的初始位置Xi,初始速度Vi,令迭代次数t=0。

3) 按全局最优选择策略确定最优粒子pgi,粒子群中的每个粒子的速度向量vi和位置向量xi按照下式更新:

vi(t+1)=ωvi(t)+c1r1(pbi-xi(t))+c2r2(gbi-xi(t))

(10)

xi(t+1)=xi(t)+vi(t+1)

(11)

式中:t为迭代次数;ω∈[0,1]为惯性权重;c1∈[0,1],c2∈[0,1]是学习因子;r1∈[0,1],r2∈[0,1]是随机数;pbi是第i个粒子的历史最优解;gbi是第i个粒子进化的全局最优解。

4) 最优解输出,本文中选取最大迭代次数最为算法结束的条件。所选定的最大迭代次数应该保证参数范围内的数据可以全部参数训练,最后输出最优解。具体优化方案如图1所示。

图1 多目标优化流程图

2 实验设置

选用TC4作为加工材料,测力平台为Kistler 9257B,刀具为4齿SN5204P,刀具直径为12 mm。试验设置如图2所示,切削参数如表1和表2所示。

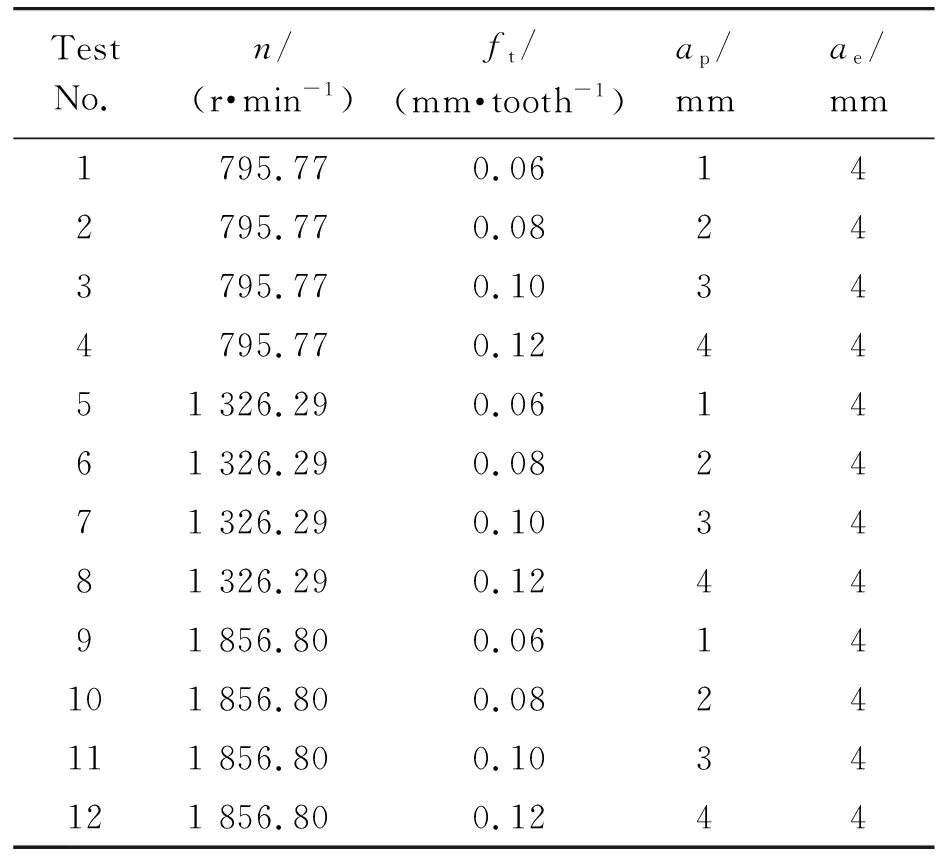
表1 切削力系数校准试验参数

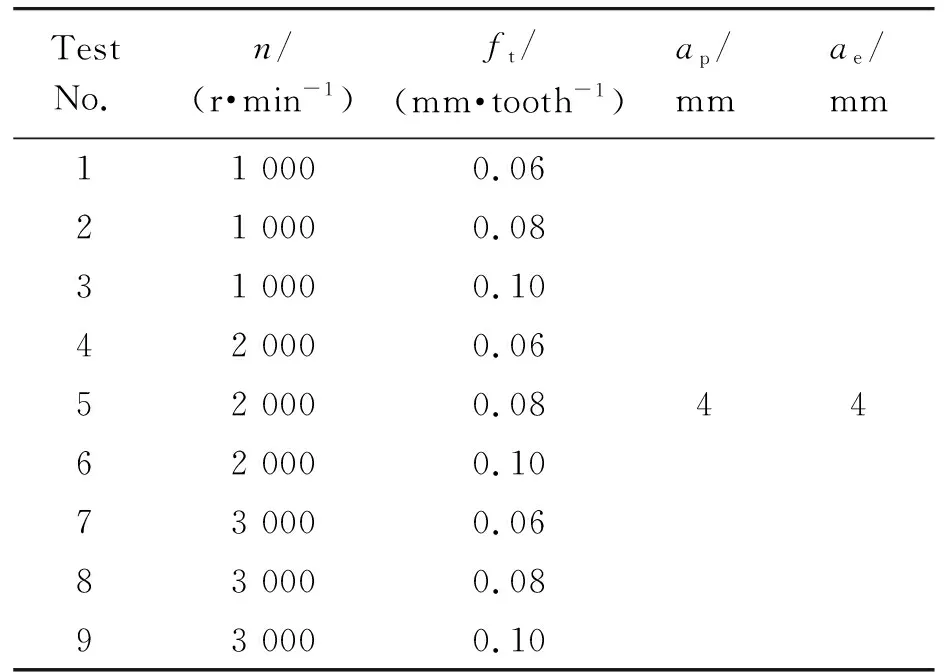
表2 刀具磨损试验参数

图2 试验设置

3 实例验证

根据实际加工要求,分别建立了材料去除率、刀具寿命和刀具寿命切削力的优化目标。本节提供了该问题的数学模型和适用的求解方法,获得了最优解,并通过实验验证了参数优化的有效性。

3.1 优化案例1

本节通过钛合金切削实验,验证了一种基于最大化材料去除率和最小化刀具磨损的多目标优化方法的工艺参数。

随着刀具参与切削的时间不断增加,刀具磨损逐渐发生。在初始磨损和正常磨损之后,磨损率继续增加。在初始磨损阶段,刀具磨损率趋于下降并变为恒定值,进入正常磨损期。当刀具磨损达到一定值时,刀具磨损率发生突变并迅速增加。为了分析控制变量对刀具磨损的影响,正常磨损阶段刀具磨损与切削长度之间的关系可以表示为:

VB=kVBL+bVB

(12)

式中:kVB为磨损曲线拟合斜率;bVB为磨损曲线拟合截距。

基于实验数据,不同切削参数下刀具磨损曲线的拟合结果如表3所示。

表3 磨损曲线拟合

依据表3的拟合结果,可以分别获得刀具磨损曲线斜率、截距与控制变量之间的变化规律,如图3所示,其关系可以表示为式(13)和式(14)。

图3 刀具磨损曲线斜率、截距随切削参数的变化规律

kVB=exp(26.52-3.557lnn+8.479lnft+
0.146 4(lnn)2-0.678 2lnn·lnft+
0.341 5(lnft)2)

(13)

bVB=exp(30.46+1.438lnn+25.46lnft-
0.126 3(lnn)2-0.222 5lnn·lnft+
4.659(lnft)2)

(14)

该关系模型的方差分析结果如表4所示,kVB和bVB的确定系数分别为0.99和0.96,非常接近1,说明模型具有较好的准确度。

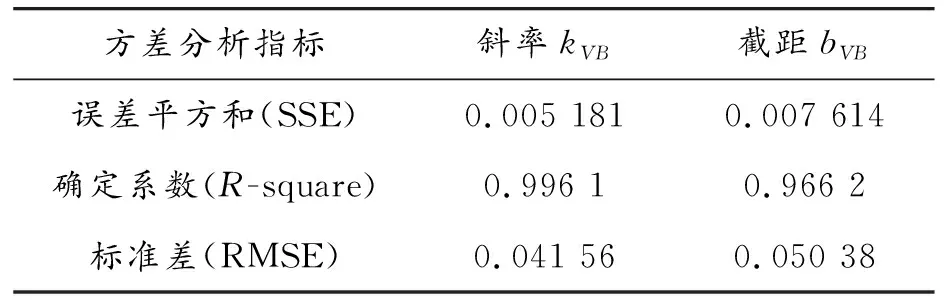
表4 刀具磨损曲线拟合方差分析

在正常磨损阶段,切削长度为L时,刀具磨损量VB(L)可以表示为:

VB(L)=exp(26.52-3.557lnn+8.479lnft+
0.146 4(lnn)2-0.678 2lnn·lnft+
0.341 5(lnft)2)×L+exp(30.46+
1.438lnn+25.64lnft-0.126 3(lnn)2
-0.222 5lnn·lnft+4.659×(lnft)2)

(15)

综上,多目标优化函数可以表示为:

(16)

目标函数中的相关参数信息见表5。目标函数变量设定值见表6。

表5 案例1多目标优化参数设置

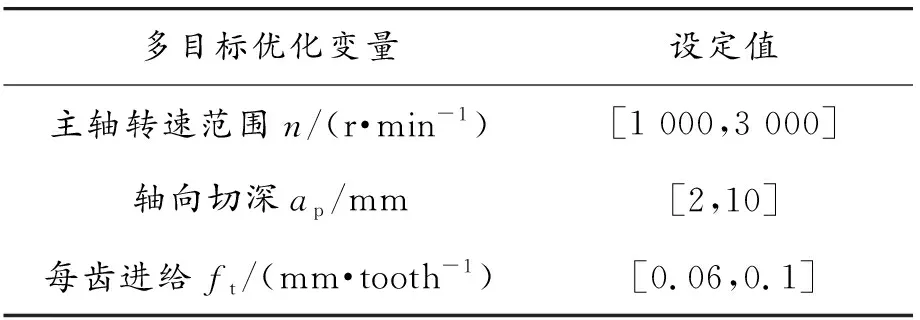
表6 案例1多目标优化变量范围

基于Pareto支配的多目标PSO优化算法中所涉及的参数见表7。

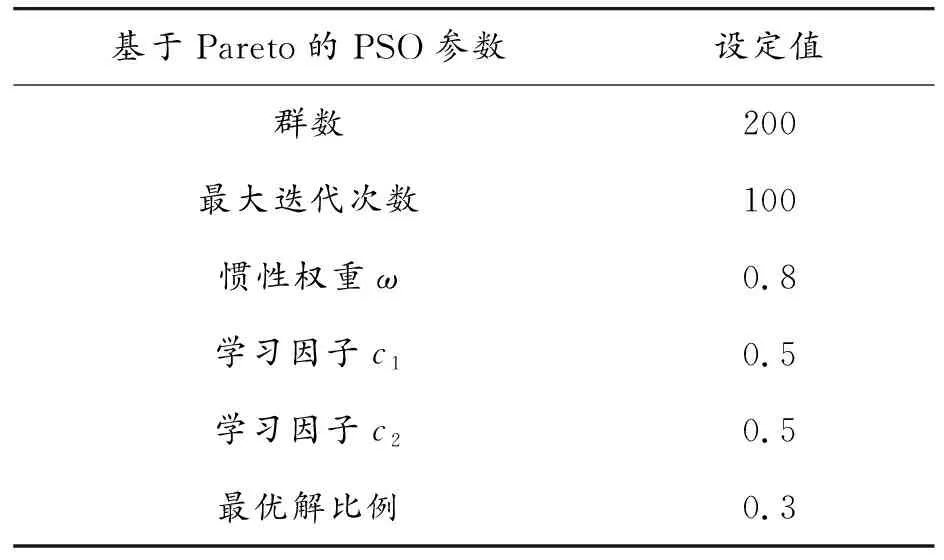
表7 案例1多目标优化参数设置

基于上述优化算法,给定不同的刀具磨损阈值VB(100、200、300 μm),分别可得到Pareto解集(60个解),Pareto前沿如图4所示,可以设定横坐标表示材料去除率MRR,纵坐标表示铣削长度L,每一个点对应一组切削参数及相应的材料去除率和铣削长度值。

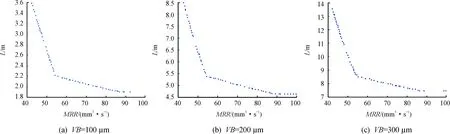
图4 案例1优化后的解集

图4中的每一个数据点都对应一组切削参数(n,ap,ft),每个点所在位置的横纵坐标分别对应该参数下的材料去除率和当前刀具磨损量下的铣削长度。从图4中Pareto前沿的变化趋势可以看出,在给定的切削参数范围内,材料去除率MRR越小,刀具铣削长度L越大。Pareto前沿中任意点所对应的解,都是求解出的优化参数。

案例1优化后的参数范围见表8。表8中的数据可以说明,工艺参数的范围在刀具磨损的初期阶段处于较高的水平,从而达到材料去除率最优的目的,随着刀具磨损的不断加剧,参数范围表现出变小的趋势,这是由于需要综合考虑2个优化目标的结果。

表8 案例1优化后的参数范围

另外,从表8可以看出,改变刀具磨损阈值时,控制变量的最优解区间变化不明显,而刀具最长寿命为刀具磨损量VB=300 μm。因此,以刀具磨损阈值VB=300 μm为例,可根据优化解集中各数据对应不同的材料去除率和切削长度,将切削长度较大区间划分为切削长度优先区间,材料去除率较大区间划分为材料去除率优先区间,中间部分则划分为兼顾区间。

如图5所示,刀具寿命优先区间的加工参数具有较长的铣削长度和相对较低的材料去除率,该区间适用于产品交付速度快的生产参数优选。兼顾区间的加工参数使得铣削长度和材料去除率更加均衡,该区间适用于无特定限制要求的生产参数优选。材料去除优先区间具有较高的材料去除率和相对较短的铣削长度,该区间适用于刀具数量不足的生产参数优选。

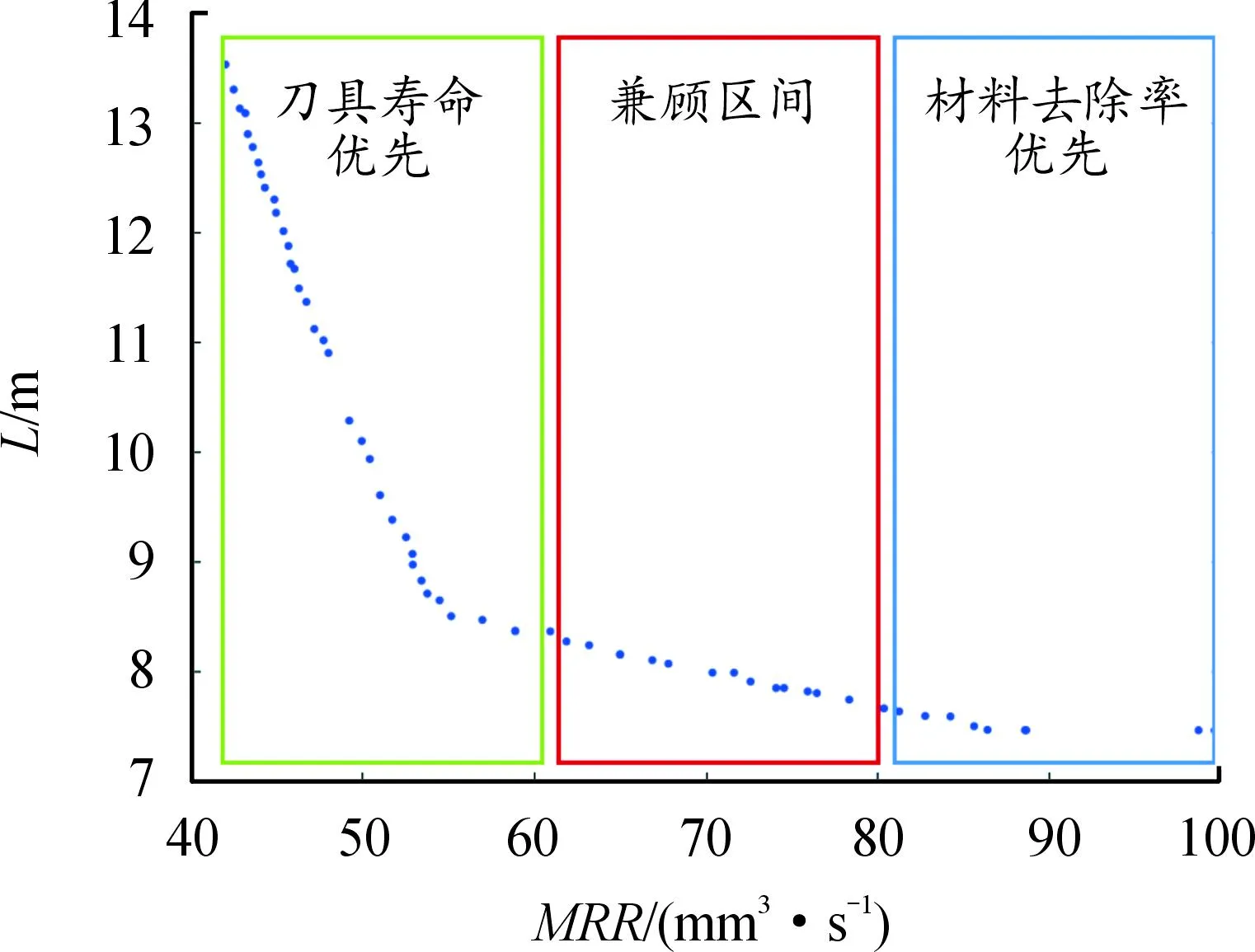
图5 案例1优化后的解集分区

为验证所提出方法的准确性在3个区间中分别选取一组参数进行试验验证,具体加工参数与Pareto解见表9。

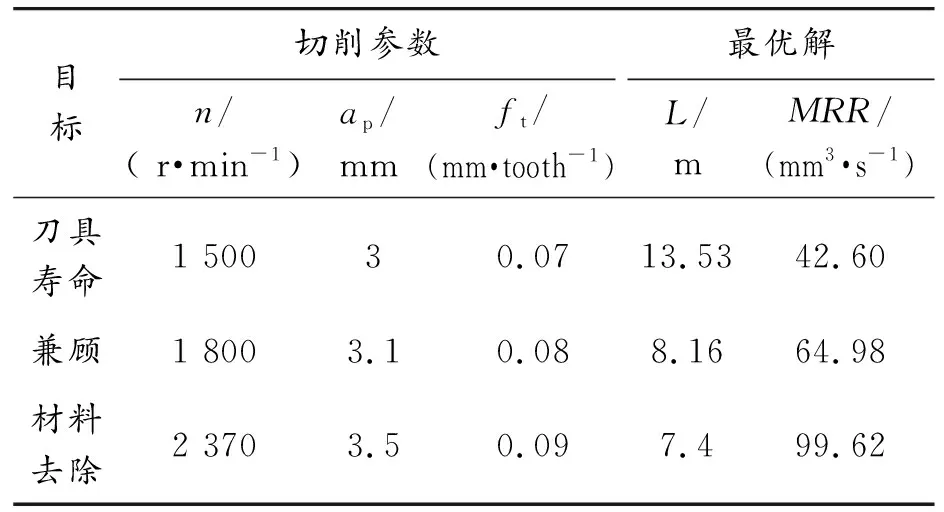
表9 案例1优化验证试验参数

表10为不同区间内选择的3组切削参数下对应的材料去除率和刀具磨损的预测误差。从表10可以看出,刀具寿命优先区间选取第1组参数(表9的第1组参数),材料去除率最小,预测误差为3.81%,刀具磨损的预测误差为4.72%。这是由于以刀具寿命为优先值考虑的话,切削用量比较保守,材料去除率低。第3组参数位于材料去除优先区间内,所以其材料去除率最大,但随之带来的是刀具磨损也较大,切削用量相对较大。而兼顾材料去除率和刀具寿命的第2组切削参数,刀具磨损是3组中最小的,并且材料去除率比第一组参数高,说明确实有兼顾二者共同的影响,大大延长了刀具寿命,从而减少了加工成本,也保证了加工质量,验证了所提出的模型的预测准确性。

表10 案例1优化算法验证结果

3.2 优化案例2

通过钛合金切削试验对工艺参数展开基于切削力最小和刀具磨损最小的多目标优化方法进行验证,本节中的实验设置与3.1节案例一相同。刀具磨损可由式(15)获得。为了分析控制变量对切削力的影响,首先应建立切削力系数与控制变量之间的关系:

K=f(n,ap,ft)

(17)

式中:K为切削力系数。

根据表1中的参数进行切削力系数校准试验,结果如表11所示。

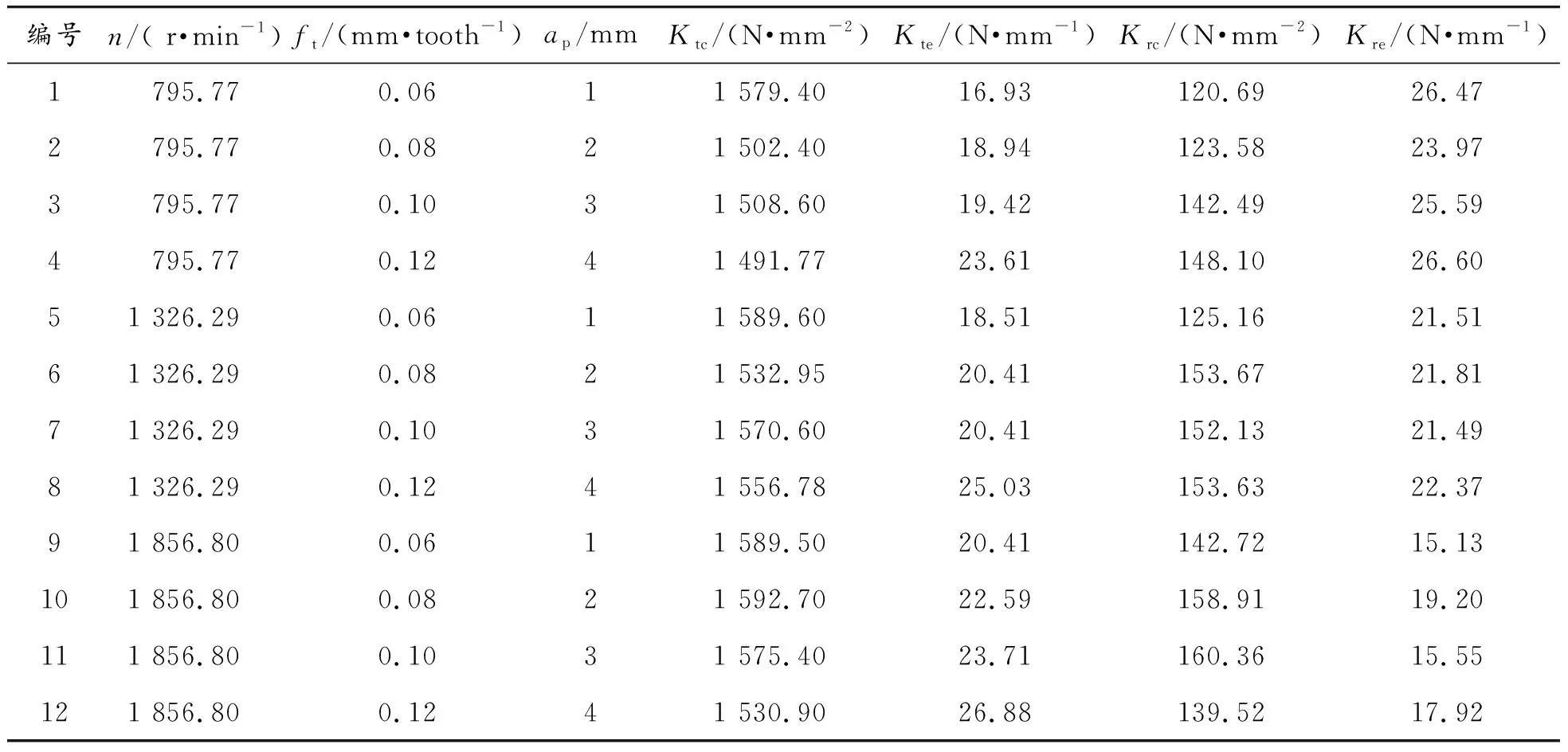
表11 切削力系数标定结果

依据表11的拟合结果,可以分别获得各向切削力系数与控制变量之间的变化规律,如图6所示,其关系可以表示为式(18)-式(21)。

图6 切削力系数随切削参数的变化规律

Ktc=exp(24.02-4.602lnap-8.061ln(ft×n)+1.5lnap×ln(ft×n))×
exp(1.286[ln(ft×n)]2-0.122 8lnap×[ln(ft×n)]2-0.067 52[ln(ft×n)]3)

(18)

Kte=exp(1.552+0.060 34lnap+0.240 51ln(ft×n))

(19)

Krc=exp(-5.283-17.24lnap+6.107ln(ft×n)+5.884lnap×ln(ft×n))×
exp(-1.242[ln(ft×n)]2-0.499 8lnap×[ln(ft×n)]2-0.084 5[ln(ft×n)]3)

(20)

Kre=exp(5.922+0.249 7lnap-0.506 11ln(ft×n))

(21)

该关系模型的方差分析结果如表12所示,Ktc、Kte、Krc、Kre的确定系数分别为0.89、0.90、0.92、0.89,非常接近于1,说明模型具有较好的准确度。

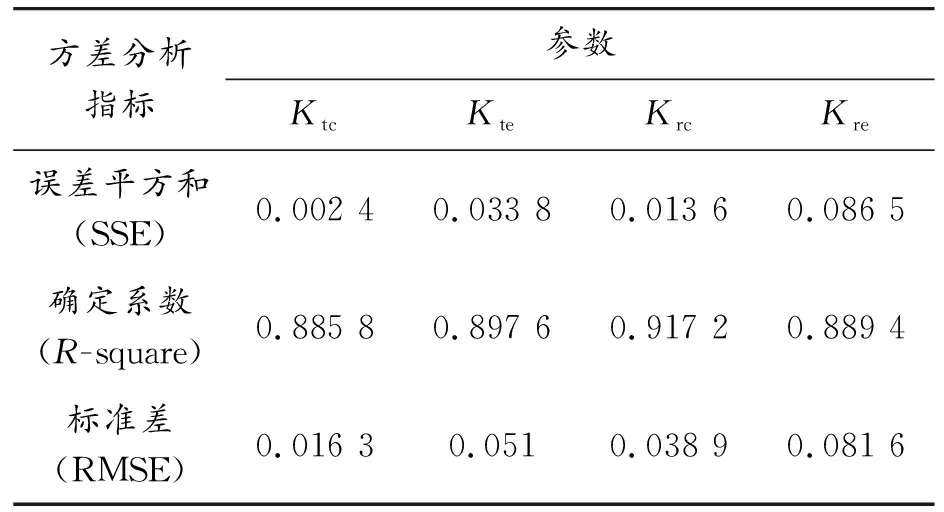
表12 切削力系数拟合方差分析

利用式(3)和式(7)可获得预测切削力,综上,多目标优化函数可以表示为:

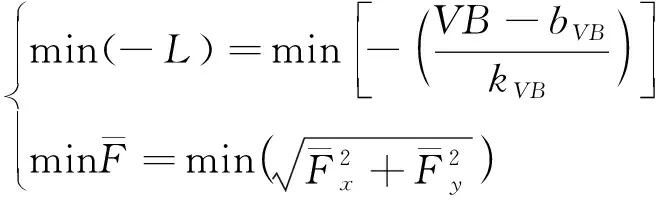
(22)

下面进行多目标优化求解,目标函数中的相关参数信息、目标函数变量的设定值以及PSO优化算法中涉及的参数如表5-表7所示。基于上述优化算法,给定不同的刀具磨损阈值VB(100、200、300 μm),分别可得到Pareto解集(60个解),Pareto前沿如图7所示,横坐标表示切削力的相反数-F,纵坐标表示铣削长度L。

图7 案例2优化后的解集

图7中的每一个数据点都对应一组切削参数(n,ap,ft),每个点所在位置的横纵坐标分别对应该参数下的切削力和当前刀具磨损量下的铣削长度。从图7可以看出,不同切削参数下,Pareto前沿的变化趋势是相同的,在设定好切削参数的范围后,切削力F越小,刀具铣削长度L越大。Pareto前沿中任意点所对应的解,都是求解出的优化参数。案例二优化后的参数范围见表13。

表13 案例2优化后的参数范围

从表13还可以看出,改变刀具磨损阈值时,控制变量的最优解区间变化不明显,尤其是主轴转速的最优区间几乎是一致的。以刀具最长寿命,即刀具磨损量VB=300 μm,将其细分为3个区间,如图8所示,刀具寿命优先区间,兼顾区间,切削力最小优先区间。

图8 案例2优化后的解集分区

为验证所提出方法的准确性在3个区间中分选取一组参数进行试验验证,具体加工参数与Pareto解见表14。

表14 案例2优化验证试验参数

表15为不同区间内选择的3组切削参数下对应的切削力和刀具磨损的预测误差。从表15可以看出,刀具寿命优先区间选取第1组参数(表14中的第1组参数),切削力的预测误差最小,为4.31%,刀具磨损的预测误差为5.41%。这是由于如优先考虑刀具寿命,则切削用量比较保守,第3组参数位于切削力优先区间内,所以其切削力虽最小,但刀具磨损却相对较大。而兼顾切削力和刀具寿命的第2组切削参数,切削力和刀具磨损都是3组中最小的,说明确实有兼顾二者共同的影响。

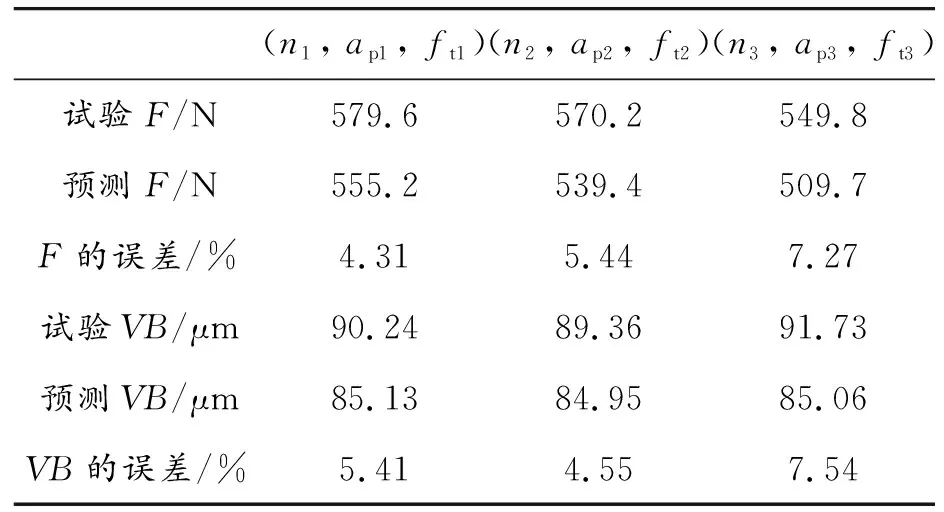
表15 案例2优化算法验证结果

3组最优参数在切削力和刀具寿命方面的优势很接近,很难直观看出优化的意义所在。因此,可以选取最优解之外的参数与最优解作对比。

选取1组最优解(n2,ap2,ft2)=(1 920 r/min,8.9 mm,0.09 mm/tooth),以及最优解外的任意一组参数(n4,ap4,ft4)=(1 500 r/min,10 mm,0.1 mm/tooth),设定刀具磨损量相同,在试验中对切削力和铣削长度进行对比,结果如表16所示。

表16 优化效果对比

分别在(n2,ap2,ft2)和(n4,ap4,ft4)的加工参数下,使刀具磨损量VB=100 μm,从表16可以明显看出,优化后的参数无论在切削力与铣削长度上都有明显优势。与任意选择的切削参数相比,优化后的参数不仅使切削力减小了13%,还使刀具磨损减少了20%。因此,优化后的参数对刀具寿命具有明显的提升作用。