空压机负荷预测与智能调度算法研究

2024-02-05王华秋

重庆理工大学学报(自然科学) 2024年1期

王华秋,张燕

(重庆理工大学两江人工智能学院, 重庆 401135)

0 引言

中国空气压缩机产业起步晚,在创新方面落后于国外,在国内市场份额相对较小。我国空压机工业要实现自身的变革与提高,必须进行深层次的研究与实践。对空压机的台数调度进行研究,在负荷预测基础上对机组进行调度分配,达到供需平衡,提高设备的工作效率,降低能耗。近年来,不同预测模型和机组组合方法受到广泛关注。

由于考虑不全面、历史数据量大,传统的负荷预测模型准确率不高,而深度学习不需要人工提取特征,因此在大数据时代受到广泛关注。宋晓华等[1]建立了一种基于Gabor-LSTM-XGboost的两级预测模型,提高了负荷预测的准确率。臧海祥等[2]利用多维信息融合的特点,结合卷积神经网络,对多任务的短期负荷进行预测。陈文成等[3]证明了GA-BP神经网络模型具有较好的预测能力。张功勋等[4]采用基于卷积神经网络的支持向量机模型,取得了较好的日负荷预测效果。王华秋等[5]利用长短时记忆网络(LSTM)预测制冷机组能源转化率,采用树种算法(TSA)改进优化运行参数。Ran 等[6]提出一种融合自适应噪声的完备集合经验模态分解、样本熵和Transformer的混合模型进行短期负荷预测。机组组合是规划阶段的措施之一。Yang等[7]提出了一种将多维萤火虫算法与局部搜索相结合的方法,将其用于求解机组组合问题。张朝炜等[8]利用改进的人工鱼群算法对大电网机组进行负荷分配。陈德树等[9]以RE并网与抽水蓄能系统为基础,对网络约束下的机组组合优化调度问题进行研究。赖伟鹏等[10]将二进制微粒群算法和混沌飞蛾相结合,给出了一种具有单时刻参数的可变机组组合优化方案。陈伟伟等[11]利用仿射补偿机制建立了一种鲁棒机组组合模型,并利用对偶理论将该模型转换为确定性的数学规划问题。

压缩空气系统的机组调度相对于其他机组调度是一个更为复杂的问题,它不仅要确保系统的经济性,还要使其安全、可靠地工作。本文中介绍了一种利用MHHO-DESN技术进行空压机负荷预测的新方法,利用MHHO算法找到能够最大限度地提高DESN预测性能的超参数,提高模型的负荷预测性能,在获得满足精度需求的每一时段的用气量预测之后,采用MHHO算法对空压机机组组合及用气量分配进行调度,降低设备能耗,从而达到节能的目的。

1 空压机负荷预测

尽管深度学习网络具有很好的学习能力,但在预测过程中,超参量的存在会对预测结果产生很大影响。利用群智能算法对深度学习结构化网络中的超参数进行优化,并将其与深度学习网络相结合,从而为后续智能调度提供参考[12]。

1.1 深度回声状态网络(DESN)

DESN[13]是一种以分层结构为基础的回声状态网络(ESN),其核心思想是通过构造一个深度结构来捕捉时间序列的动态特征,在空调负荷预测方面已有部分研究成果[14]。DESN的拓扑结构如图1所示。

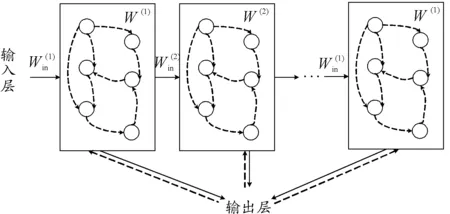
图1 DESN拓扑结构

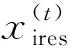
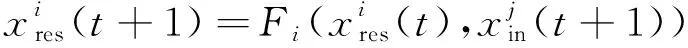
(1)

确定前一个储备池的初步状态后,通过无监督的降维技术进行编码,产生相应的编码特征。第j个编码器的编码过程为

(2)

式中:fenc(·)是编码器的激活函数,若其为恒等函数,左侧为线性降维技术。

综上所述,最后一个储备池的状态为

Hj=tj∘Fj

(3)

(4)

DESN将附加的编码器层的编码特征纳入最后的输出层中,结果输出为:

Y=fout(WoutM)

(5)

1.2 哈里斯鹰优化算法及其改进

近年来,群智能算法发展迅速,哈里斯鹰优化算法(Harris hawk optimization,HHO)由于具有更好的全局搜索性能和更少的参数调整等优势受到了越来越多的关注。将其与SVM、LSSVM等方法相结合后,相关研究在故障诊断、滚动轴承等方面取得一定成果[15-16]。

1.2.1 HHO算法

HHO算法是一种用于仿真哈里斯鹰捕猎行为的智能优化算法[17],研究内容分为3个阶段:探索阶段、探索与开发转换阶段和开发阶段。

1) 探索阶段:哈里斯鹰在特定的地点随意停留,根据式(7)寻找猎物。

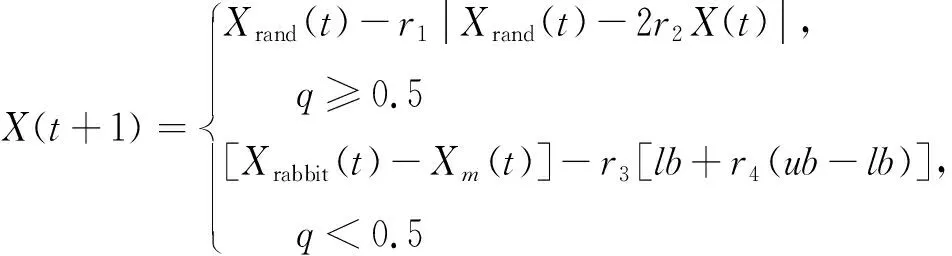
(7)

式中:Xt和Xt+1是哈里斯鹰当前和下次迭代的位置;Xrand(t)为第t次迭代哈里斯鹰的随机位置;Xrabbit(t) 为猎物第t次迭代时的位置;Xm(t)为第t次迭代时哈里斯鹰的平均位置;lb、ub是搜索空间的下界和上界;q、r1、r2、r3、r4是区间(0,1)的随机数。

2) 探索与开发转换阶段:通过猎物的能力方程实现从探索到开发的过渡,其模型表示为

(8)

其中:E0为猎物能量的初始状态,是[-1,1]的随机数,在每次迭代时自动更新;T是最大迭代次数;t是当前迭代次数。当|E|≥1时进入搜索阶段,当|E|<1时进入开发阶段。

3) 开发阶段:r是在[0,1]的随机数,并按r选取不同的开发策略:

① 软围攻策略。当0.5≤|E|,r≥0.5时:

X(t+1)=ΔX(t)-E|JXrabbit(t)-X(t)|

(9)

其中:ΔX(t)=Xrabbit(t)-X(t)为个体位置与猎物位置的差值,J是[0,2]的随机数,表示猎物的随机跳跃。

② 硬围攻策略。当|E|<0.5,r≥0.5时:

X(t+1)=Xrabbit(t)-E|ΔX(t)|

(10)

③ 渐近式快速俯冲的软围攻策略。0.5≤|E|<1,r<0.5时:

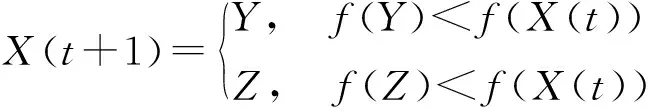
(11)

Y=Xrabbit(t)-E|JXrabbit(t)-X(t)|

(12)

Z=Y+S*LF(2)

(13)

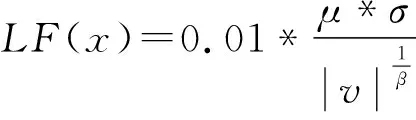
(14)

其中:f( )为适应度函数;S为范围在[0,1]的二维随机向量;LF(x)是莱维飞行表达式。

④ 渐近式快速俯冲的硬围攻策略。|E|<0.5,r<0.5时:

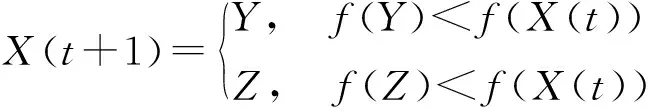
(15)

Y=Xrabbit(t)-E|JXrabbit(t)-Xm(t)|

(16)

Z=Y+S*LF(2)

(17)

1.2.2多策略改进的哈里斯鹰优化算法(MHHO)

HHO算法与莱维飞行方法结合用于求解多维复杂问题时,具有参数少、计算精度高、易于操作等优点。然而,该算法收敛速度较低,且会在搜索过程中产生局部最优,因此对算法进行下述改进:

1) Sobol序列初始化种群

HHO算法利用随机函数对群体进行初始化,结果具有很强的随机性,可覆盖一定区域,但同时存在不确定因素。在随机初始化后,无法保证其分布的均匀性,甚至可能出现较为集中的情况,导致缺乏种群多样性和搜索时间长。为解决这些问题,采用Sobol序列进行初始化群体的映射,提高对高维序列的处理效率,同时兼顾个体的分布均匀性,使得个体在空间中均匀分布,从而提高初始群体质量,为算法的下一步搜索提供有效条件,从而加速收敛。其表达式如下:

X=lb+r(ub-lb)

(18)

其中:[lb,ub]为最优解的取值范围;r为Sobol序列产生的[0,1]范围随机数。

2) 随机收缩指数函数

在HHO算法中,逃逸能量E被用于从探索到开发的过渡。因迭代后半部分只进行局部搜索,容易陷入局部最优,故在原基础上引入随机收缩指数函数,对应能量方程为:

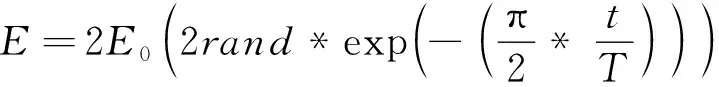
(19)

3) 正余弦优化算法

正余弦优化算法(sine cosine algorithm,SCA)是于2016年提出的一种新型智能优化算法[18]。该算法产生多个初始随机候选解,并根据正弦和余弦的数学模型向外或向最优解方向波动,通过多个随机变量及自适应变量求出目前解的位置,使得能在空间内寻找不同的区域,从而在全局搜索与局部开发之间实现有效均衡,避免陷入局部极值。

(20)

综上所述,对于初始化种群,采用Sobol序列对群体进行初始化,以改善初始种群的质量;在能量转化过程中,为防止陷入局部最优,使用随机收缩指数函数;在开发过程中,使用SCA算法对HHO算法的位置更新进行改善。哈里斯鹰多策略优化算法步骤如下:

步骤1Sobol序列种群初始化,根据搜索空间每一维的上界和下界对每个个体初始化;

步骤2根据目标函数计算哈里斯鹰个体的适应度值;

步骤3猎物能量E由式(19)进行更新;

步骤4若|E|≥1,全局探索的位置更新由式(7)执行;

步骤5若|E|<1,r<0.5,局部探索的位置更新由式(11)和式(15)执行;

步骤6若|E|<1,r≥0.5,局部探索位置更新由式(20)执行;

步骤7计算步骤4、5、6的适应度值,如果得到更好的适应度值,则更新全局最优解和全局最优适应度值;

步骤8评估最终条件,如果满足,程序运行结束,并输出最优值及最优解;否则,继续执行步骤2。

2 智能调度

根据负荷预测,智能调度可在一定时间内动态地决定机组的最优数量和最优组合,从而预先建立最优的调度。在满足负荷供需平衡等约束条件的情况下,能够有效改善压缩机工作性能,节约能源。

2.1 目标函数

智能调度的压缩空气系统可使空压机在使用过程中的能耗最小化,其能耗包含压缩机的电力消耗和压缩机启动时的能耗。因此,目标函数为:

Ui,t(1-Ui,t-1)Si]

(21)

式中:N为空压机台数;T为机组调度周期;Ui,t为t时刻第i台空压机的运行状态,Ui,t=1代表运行,Ui,t=0代表停机;Qi,t为t时刻第i台空压机的用气量;F(Qi,t)为第i台空压机在t时刻的工作能耗;Si为第i台空压机的开机能耗。

空压机的工作能耗F(Qi,t)为空压机工作过程中的耗电量,机组的耗能特性函数通常用二次函数来表达,其表达式为

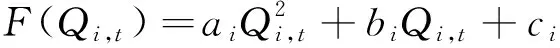
(22)

式中:ai、bi、ci为第i台空压机的性能常数。

2.2 约束条件

1) 负荷均衡约束

(23)

式中:Pt为t时刻所需的系统负荷。

2) 负荷备用约束

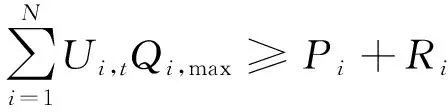
(24)

式中:Ri为t时刻负荷备用需求,选择5%的Pi作为备用容量;Qi,max为第i台空压机的最大产气量。

3) 单台机组产气量约束

Ui,tQi,min≤Qi,t≤Ui,tQi,max

(25)

4) 空压机启停约束

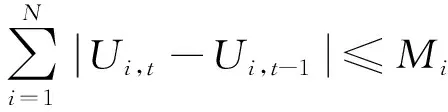
(26)

式中:Mi为空压机i每日最大停机次数,本文取Mi=3。

5) 0-1变量约束

(27)

3 空压机负荷预测及智能调度模型

在DESN模型中存在着多个根据先验知识进行调整的超参数,如泄漏率、频谱半径、稀疏程度等。在相应的数据集合中,如何找到最优超参数是一个亟待解决的问题。本文中利用MHHO-DESN建立了空压机负荷预测模型,运用MHHO算法实现了DESN模型中的超参数自动优化,并以DESN模型预测和实测数据的偏差RMSE为优化目标。在得到预测数据之后,利用MHHO算法对空压机组进行台数调度及用气量分配。空压机负荷预测及智能联控模型的流程如图2所示。

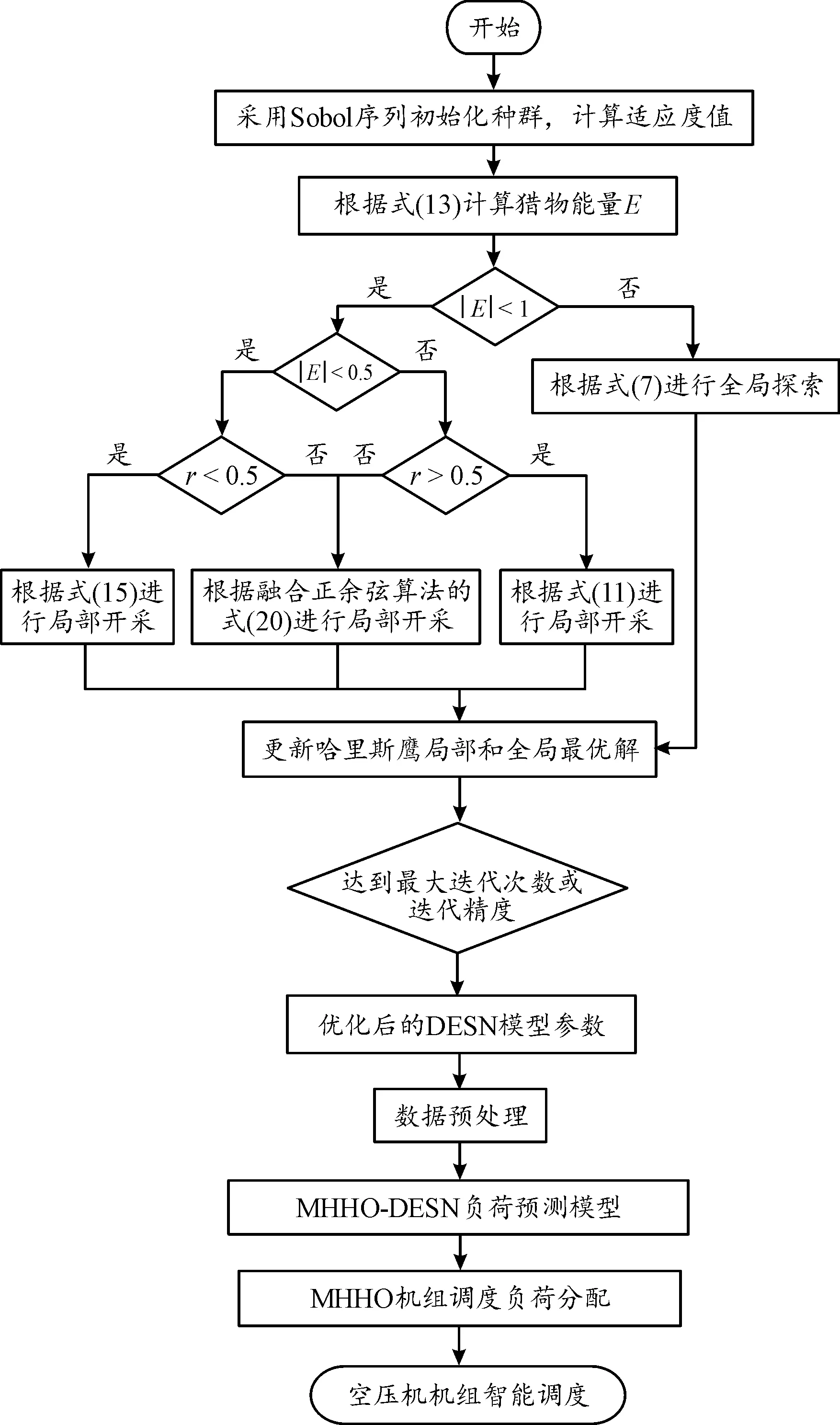
图2 空压机负荷预测及智能联控模型流程

4 实验

4.1 数据预处理

以某工厂2021年11月份连续3周的历史数据为训练样本,以1周时间内的历史数据为测试样本。由于神经网络对输入数据的变化非常敏感,需要对其进行预处理,因此利用线性归一化法对数据进行归一化处理,使负载数据缩放至[0,1]。

4.2 预测结果评估方法

预测空压机一天24 h的负荷,预测结果的评估主要有以下几种指标:

(30)

4.3 参数灵敏度分析

对于非稳定负荷预测,储备层的神经元数量对预测结果的影响最大。当泄漏率L=1、谱半径SR=0.9、稀疏程度S=0.1、储备池的层数n=3时,通过对不同储备池深度的预测,对其优越性进行评估。在表1中显示了储备池深度对DESN模型的预测性能的影响。

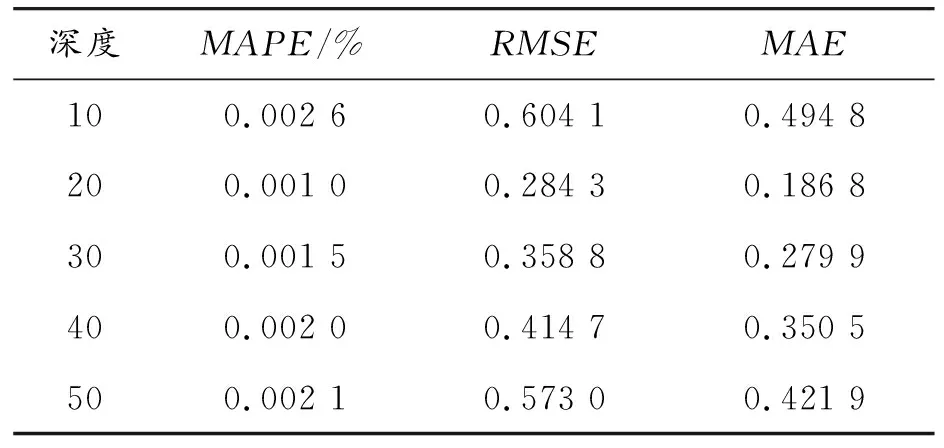
表1 储备池深度对DSEN的预测性能影响

从实验和结构的角度来看,随着储备池深度的增加,惯性增大,对于不稳定负荷的预测相对薄弱,且不容易改变其固有属性。但如果储备池的深度太浅,就会缺乏非线性的学习能力,不能达到更好的非线性拟合,因此储备池的深度选取尤为重要。由表2可知,在DESN网络中,当网络中的神经元数目为20时,其预测准确率最高。在后续实验中,将各对比方法中隐藏层神经元数目设定为20,以实现各对比算法的可控性,对其性能进行合理比较。

表2 不同算法网络参数设定

4.4 对比算法设置

为评估基于MHHO-DESN网络的空压机负荷预测模型性能,选取BPNN、LSTM、DESN、HHO-DESN、SCA-DESN、MHHO-DESN等不同类型的网络进行比较。所有网络均基于同一历史数据进行预测。表2列出了各种网络的参数设定。HHO、SCA、MHHO等优化算法的参数设置如表3所示。

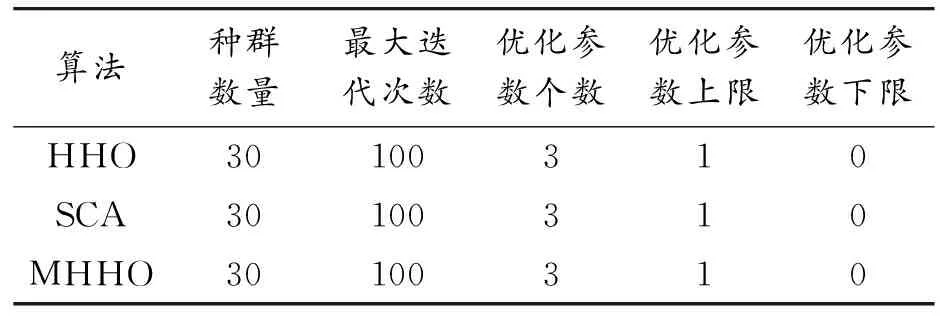
表3 不同优化算法参数设定

4.5 预测性能分析

利用BPNN网络、LSTM网络、DESN网络、MHHO-DESN网络对空压机一天24 h的负荷进行预测,得到相应的预测结果(图3)和预测误差绝对值(图4)。其中,图3局部放大了第19 h的预测结果,图4为各模型预测结果与实际数据误差的绝对值比较。网络预测结果评价指标见表4。

表4 网络预测结果评价指标

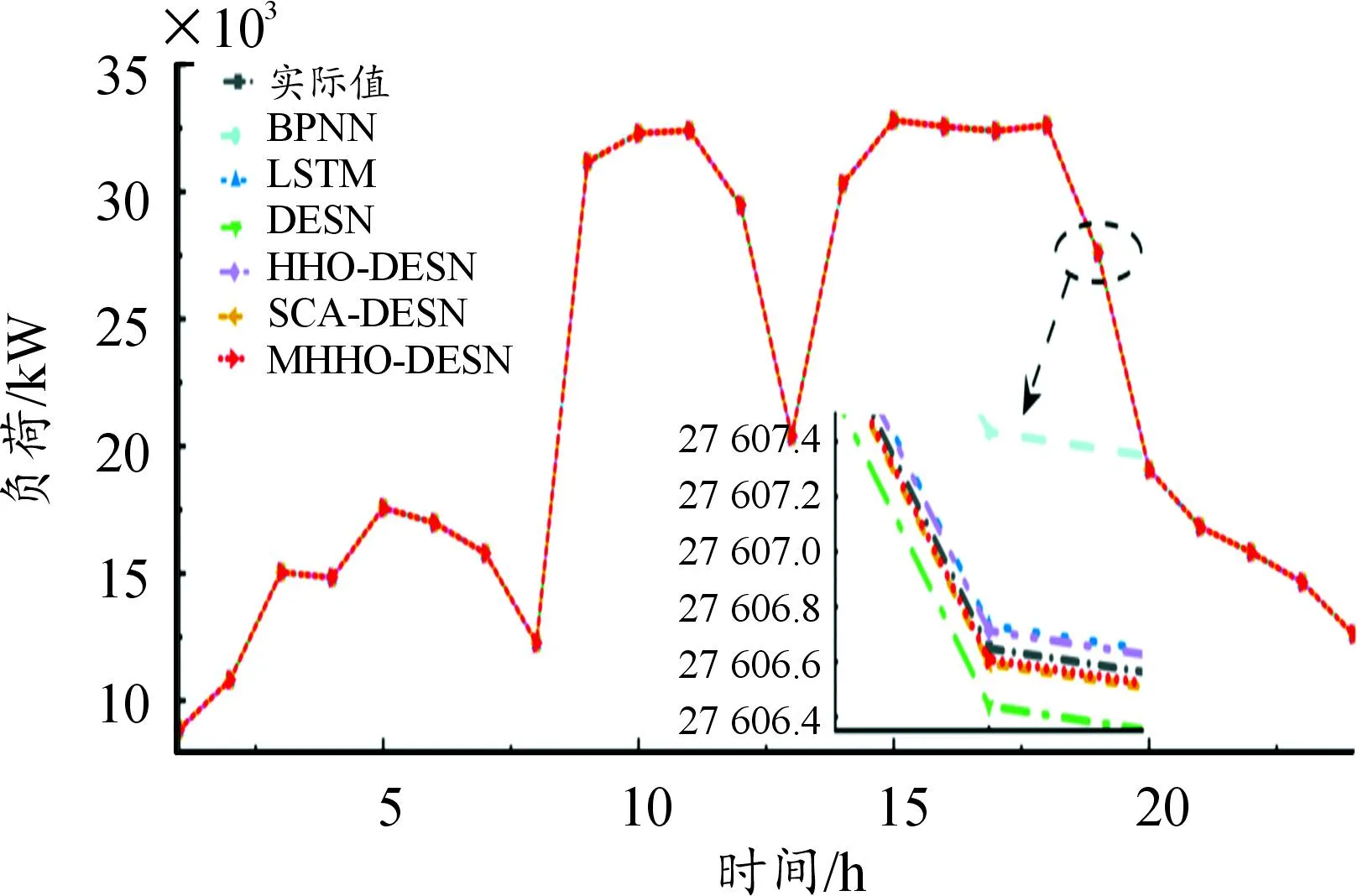
图3 网络预测结果

图4 网络预测误差绝对值

从表4可知,MHHO-DESN模型相较于其他预测模型在负荷预测上预测效果更优。相对于BPNN模型,MHHO-DESN模型的MAPE值、RMSE值、MAE值分别减小了0.007 371%、1.993 7、1.241 6;相对于LSTM模型,评估值分别减小了0.002 671%、0.873 2、0.533 0;相对于DESN模型,评估值分别减小了0.000 771%、0.225 2、0.140 3;相对于HHO-DESN模型,评估值分别减小了0.000 357%、0.113 2、0.062 3;相对于SCA-DESN模型,评估值分别减小了0.000 477%、0.136 0、0.083 9。由此可见,MHHO-DESN模型相对于其他模型能够在周期性、非线性的空压机负荷数据中更好地完成负荷预测,且MHHO算法相较于其他优化算法在优化DESN模型参数时所达到的预测效果更优。从图3、图4可以看出,MHHO-DESN模型预测性能更优;MHHO算法可以在DESN网络中找到更好的网络参数,从而得到更佳的预测效果。利用MHHO算法优化得到的DESN参数如表5所示。

表5 MHHO-DESN优化前后超参数值

4.6 机组组合仿真分析

对10台空压机进行机组调度,各个空压机组的性能参数见表6。选取预测数据来进行负荷分配,采用系统负荷的5%作为备用容量,得到各时段的用气量如表7所示。一天24 h所需总用气量为551 489 m3。

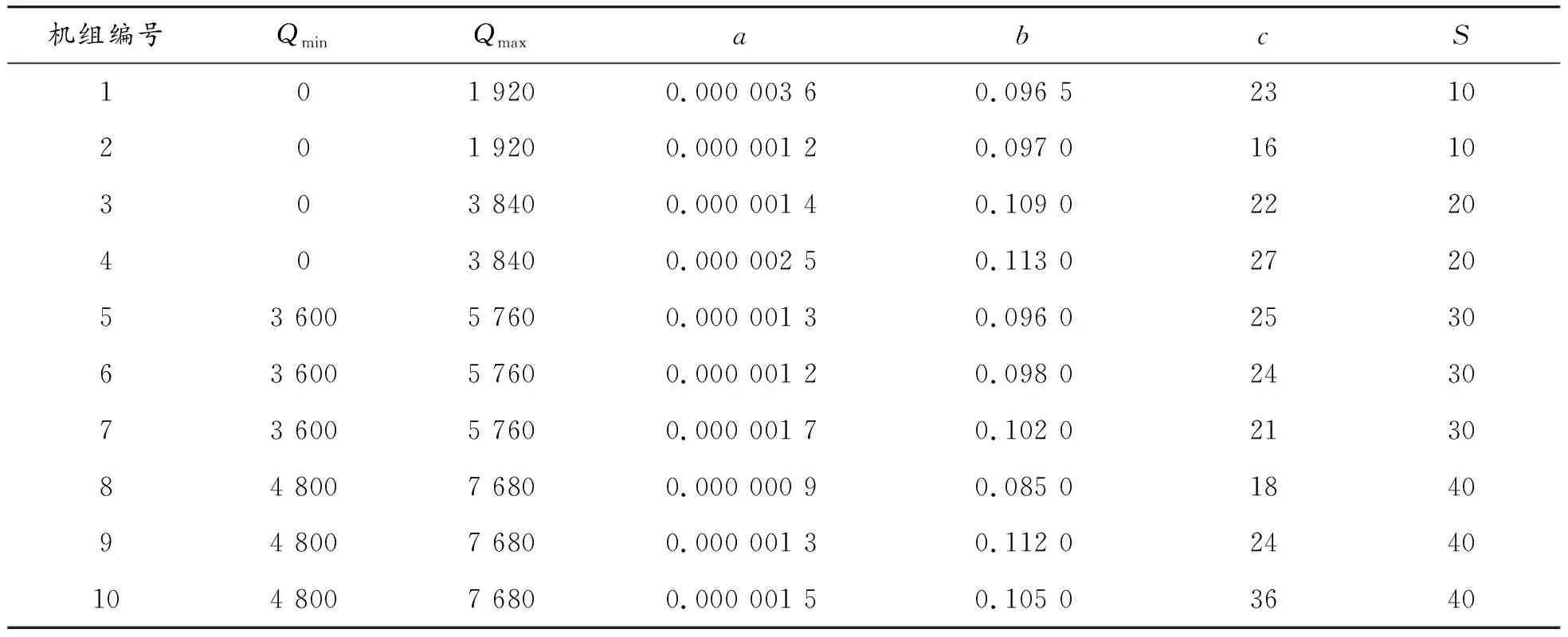
表6 各机组性能参数

表7 系统各时段用气量 m3

采用HHO算法、SCA算法和MHHO算法对空压机机组各时段负荷进行分配,计算结果见图5和表8。

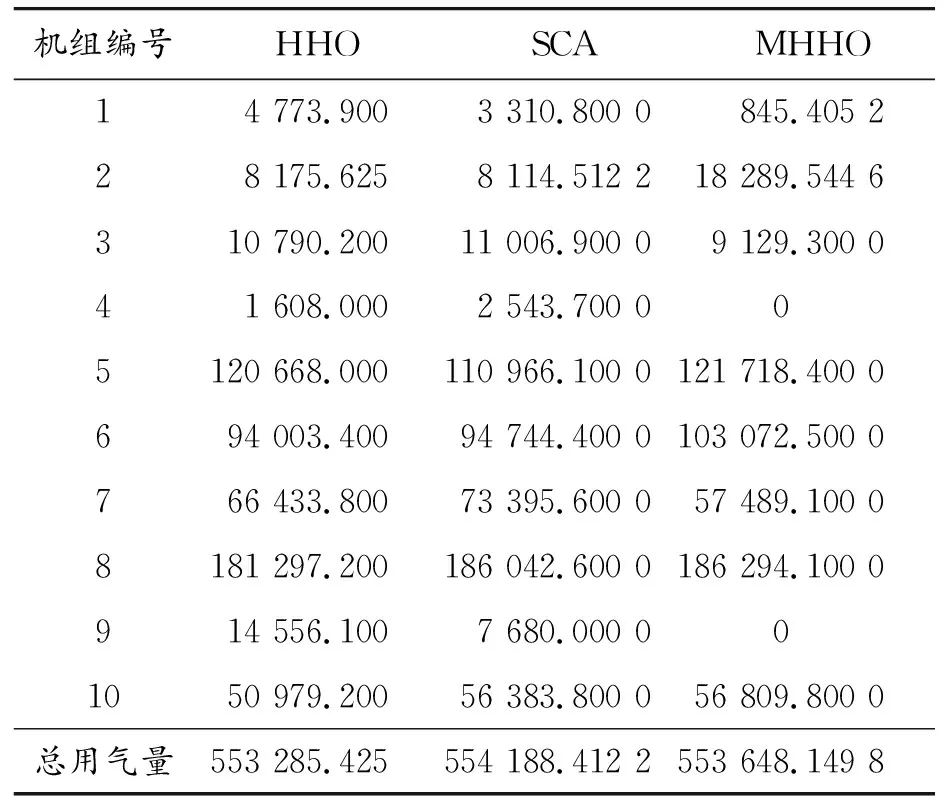
表8 各机组提供负荷 kW

由图5可知,在不同算法条件下,各机组的用气量不同。此外,HHO具有很强的局部寻优能力,容易陷入局部最优,而SCA可以有效地避免局部最优,二者结合起来可以得到很好的求解效果。各算法分配调度的总能耗:HHO算法为58 782 kW,SCA算法为58 855 kW,MHHO算法为58 437 kW。可以看出,MHHO算法相比HHO算法,能耗减少了345 kW;相比于SCA算法,能耗减少了418 kW。实验结果表明,所提MHHO算法相对于HHO算法和SCA算法,能够更好地对空压机机组进行分配调度。MHHO算法在满足约束条件时对机组进行分配调度的能耗最小,MHHO算法对各时刻机组负荷分配见表9。