任意起伏地形下重力异常三维正演及并行计算

2024-02-04戴世坤朱德祥张莹李昆陈轻蕊凌嘉宣田红军

地球物理学报 2024年2期

戴世坤,朱德祥*,张莹,李昆,陈轻蕊,凌嘉宣,田红军

1 中南大学有色金属成矿预测与地质环境监测教育部重点实验室,长沙 410083 2 中南大学有色资源与地质灾害探查湖南省重点实验室,长沙 410083 3 中南大学地球科学与信息物理学院,长沙 410083 4 西南石油大学地球科学与技术学院,成都 610500

0 引言

重力勘探广泛用于油气勘探、金属矿勘查、地球内部构造、区域地质构造以及环境地球物理等研究领域.研究针对大规模复杂条件下重力异常场高效、高精度三维数值模拟对重力异常反演以及人机交互解释有着重要作用.重力数值模拟方法按大类主要可分为空间域和频率域方法.

空间域方法中,Nagy(1966)、Li和Chouteau(1998)及Talwani和Ewing(1960)分别推导了长方体、直立棱柱体以及多面体的解析解,徐世浙(1984)、Paul(1974)、Barnett(1976)、Kwok(1991)以及 García-Abdeslem(1992)利用高斯公式将体积分转化为面积分;Ren等(2017)针对大规模三维重力异常正演开发了一种多极子算法,对复杂地形适应性好,计算精度高,速度快;Ren等(2018)通过散度定理,将体积分转化为线积分,导出线积分的精准解,进而得到重力场以及梯度张量精确解;Zhong等(2019)通过体积分与面积分的转化,利用高斯-勒让德积分公式计算多项式密度分布的几何体重力场以及重力梯度张量,能很好地解决全球尺度的重力建模问题;也有学者利用数值模拟算法(Farquharson and Mosher,2009; Zhang et al.,2004; Cai and Wang,2005; Jahandari and Farquharson,2013)进行三维重力异常数值模拟计算,取得了较好的效果.空间域方法对于异常体简单,存在解析解的模型效果好,对复杂条件下重力场三维数值模拟频率域方法具有更大的优势(Pedersen,1978,1985; 熊光楚,1984; 冯锐,1986;Chai and Hinze,1988; Parker,1973; 徐世浙,2007;王万银等,2009; 王万银,2012;Wu and Tian,2014; Dai et al.,2018; 戴世坤等,2020).相比于空间域,频率域表达式简洁,计算效率高效,但其精度受傅里叶变换的影响.快速傅里叶变换算法(FFT)的出现提升了离散傅里叶变换的计算效率,使得频率域重力异常正演计算效率高.但标准傅里叶变换存在截断效应,通过扩边能降低这种影响(Caratori Tontini et al.,2009);针对精度低问题,柴玉璞(1996)证明了傅里叶变换离散化定理,该定理揭示了函数离散值与谱离散值之间的关系,并据此给出了傅里叶变换数值计算理论-移样离散傅里叶变换理论(柴玉璞,1988; Chai,2009),并将移样离散傅里叶变换理论(SFT)应用到重磁波数域正演中,极大提升了波数域正演精度(柴玉璞和万海珍,2020);吴乐园(2014)、Wu和Tian(2014)、Wu(2016)将SFT和高斯积分节点及权系数相结合,利用高斯节点积分的高精度特点,提出了Gauss-FFT方法,避免了零波数计算,降低了截断效应的影响,在波数域正演中取得了很好的效果(Wu et al.,2019; Dai et al.,2022);Zhou等(2020)利用Gauss-FFT和NUFFT相结合进一步提高了频率域重力异常正演的适应性和计算效率;周印明等 (2020)结合傅里叶变换积分与三次样条插值函数,在此基础上进行重力异常正演,降低了连续介质重磁场数值模拟中截断效应的影响,但文中并未提及波数选取规律.

Dai等(2018)提出基于微分法的空间-波数域重力异常三维数值模拟方法,采用高斯FFT/扩边标准FFT实现了三维重力异常场快速精准数值模拟.该方法具有很好的并行性,但文献并未实现方法的并行加速方案.目前,并行计算分为CPU并行和GPU并行.CPU并行受限于计算机线程规模以及线程调度/线程同步耗时(巴振宁等,2022);相比于CPU,GPU具有更多的计算单元,可以将大规模节点计算分配给GPU线程并行执行,但是GPU仅适用于简单的计算,不适用于复杂循环运算(马琳等,2022).因此,综合多核多线程CPU以及众核GPU线程的异构体系结构是高性能计算的发展趋势(卢风顺等,2011;陈召曦等,2012;刘守伟等,2013;Qin et al.,2014; 徐云耘等,2022).

综上,本文基于微分方程的空间-波数域重力异常数值模拟算法,进行两个方面的工作:其一是实现一种基于二次插值形函数的任意傅里叶变换算法,可以根据频谱变化趋势,合理采样,提高傅里叶变换剖分的灵活性,单元内原函数采用二次插值形函数进行拟合,求得单元积分的解析表达式,积分精度高,能减小傅里叶变换带来的截断效应.其二是利用空间-波数域算法的高度并行性,解剖基于任意傅里叶变换算法的空间-波数域重力异常正演算法,实现CPU-GPU的异构体系结构并行算法,在模型正演时由CPU来控制主程序,加速了五对角方程组求解(CPU并行)和任意傅里叶变换(GPU并行),提升了算法效率.设计模型验证了算法的正确性,给出的采样规律适用于任意复杂条件下三维重力异常正演;测试了算法的并行加速比(串行计算耗时/并行计算耗时),相比CPU串行算法,CPU-GPU并行算法的速度提高了40倍以上.最后将新算法应用到实际地形重力异常正演,计算规模为721×721×421个节点的模型,耗时仅需17 s,计算效率高,适合大规模复杂条件下的重力异常数值模拟.

1 理论方法

1.1 空间-波数域重力微分法正演

基于微分法的空间-波数域重力异常正演方法从泊松方程出发,沿水平方向进行二维傅里叶变换,得到不同波数下的常微分方程,结合准确的边界条件,采用有限单元法进行求解,将三维问题转化为多个一维问题,减少了计算量和存储量需求,有效地提高了三维重力异常正演的计算效率.原理详见文献(Dai et al.,2018),本文仅简要介绍.

重力位U与空间域密度满足泊松方程(Blakely,1995):

(1)

其中,U为重力位,(x,y,z)为空间观测点坐标,G为万有引力常量6.67×10-11N·m3·kg-2,ρ为空间域密度.对式(1)沿水平方向做二维傅里叶正变换,得到空间-波数域常微分方程:

(2)

式(2)结合上下边界条件得到空间-波数域重力异常正演的边值问题(Dai et al.,2018),采用基于二次插值的一维有限元方法求解(徐世浙,1994),采用追赶法(续小磊和马丁,2013)求解最终构成的五对角线性方程组,得到空间-波数域重力位.根据重力位和场之间的关系可得到空间-波数域重力场,最后利用水平方向二维傅里叶反变换得到空间域重力异常场.

在进行空间-波数域重力异常正演计算时,正反傅里叶变换和求解方程组两部分具有高度并行性,且二维傅里叶正反变换耗时占整个算法的90%.Dai等(2018)采用标准FFT和高斯FFT实现傅里叶变换,这两种方法都需均匀剖分,采样不灵活;且文献(Dai et al.,2018)未实现算法并行.为了实现任意采样及进一步提升计算效率,本文引入一种基于二次插值形函数的傅里叶变换算法,该算法采样灵活,通过分析重力异常离散谱确定谱能量集中的范围,能精准、灵活选取波数,且基于二次插值形函数求得傅里叶变换积分的解析解,计算精度高.将正反傅里叶变换和求解方程组两部分基于CPU-GPU的异构体系结构实现了并行加速,提高了整个算法的计算效率.

1.2 任意傅里叶变换

1.2.1 任意傅里叶变换理论

本文空间-波数域重力异常场数值模拟算法中采用的二维傅里叶变换对(Blakely,1995)如下,

(3)

式中,f(x,y)表示空间域场,F(kx,ky)表示对应的二维频谱.

本文以二维傅里叶正变换式(3)为例,说明本文基于二次插值形函数的任意傅里叶变换算法的计算过程.

在实际应用中,模拟区域有限,设x方向范围:xmin～xmax,y方向范围:ymin～ymax,此时式(3)可以写为

(5)

本文提出的基于二次插值形函数的傅里叶变换算法首先将式(5)的二重积分转化为两个一重积分,可写为

(6)

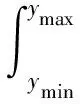
(7)

式中,Fx(kx,y)为对x积分得到的谱函数.计算式(6)和式(7)两个一重积分,可得二维傅里叶变换的二维频谱.

将计算区域采用均匀或非均匀的剖分方式沿着x和y方向离散为Mx×My个单元,每个单元内采用二次插值的形函数拟合空间域场,则节点总数为Nx×Ny.以式(6)为例,可写为

(8)

式中ej表示第j单元,令第j个单元的三个节点坐标为(xj1,xj2,xj3),xj2为单元ej中间节点,满足关系式xj1+xj3=2xj2.单元内采用二次插值的形函数拟合函数f(x,y)(徐世浙,1994),则有

f(x,y)=Nj1f(xj1,y)+Nj2f(xj2,y)+Nj3f(xj3,y),

(9)

(10)

令

(11)

式(11)中I(xj1,kx),I(xj2,kx),I(xj3,kx)为沿x方向第j个单元上三个节点的傅里叶变换积分系数,该积分系数可求得解析解.式(10)可写为

(12)

式中,

(13)

同理,式(7)可写为

(14)

式中,J(yj1,ky),J(yj2,ky),J(yj3,ky)分别为沿y方向上第j个单元的傅里叶变换节点积分系数,式中(yj1,yj2,yj3)分别为y方向第j个单元的三个节点坐标.节点积分系数推导计算方法与I(xj1,kx),I(xj2,kx),I(xj3,kx)相同,此处不再赘述,直接写出表达式:

(15)

从式(13)和式(15)可以看出,当x和y方向剖分固定时,单元形函数不变,两个方向的节点积分系数可提前计算出并存储,重复利用,减少冗余计算,提高计算效率,并且不同波数下积分系数相互独立,可并行性高.对于二维傅里叶反变换式(4),推导过程与正变换类似,不再赘述.

1.2.2 采样规则

任意采样点数FFT算法提出了离散频率取值方式(陈龙伟等,2016),标准FFT存在截断效应.扩边FFT能减小这种误差,其本质是扩边之后波数域基频减小,提高了计算精度;Gauss-FFT作为一种结合高斯点数的偏移采样傅里叶变换算法,截断效应小,计算精度高(吴乐园,2014),其原因是Gauss-FFT基于FFT采样定理,在基频单元内将采样点加密并偏移,加密点数为高斯点个数,偏移距离为高斯偏移距离,能有效提高积分计算精度.这两种FFT算法在计算离散频谱时均利用了采样定理,要求空间域和频率域均匀采样,无法实现非均匀采样.此外,为满足精度要求,扩边FFT和4个点的Gauss-FFT需要更多的波数,降低了计算效率.

本文提出的基于二次插值形函数的任意傅里叶变换算法,在空间域和波数域任意剖分,且能根据波谱能量分布灵活采样.其中,波数选取范围可延用采样定理,由于波数关于零值点的对称性,所以在波数选取时令正波数与负波数互为相反数,这里只给出正波数选取规则.

由采样定理可知,波数最大值由最小网格间距决定.设空间域最小网格间距为Δxmin,Δymin,可知kx波数的正波数采样范围为[Δk,kxmax],ky波数的正波数采样范围为[Δk,kymax],式中:

(16)

基频Δk作为基本单位:

(17)

式(17)中tmax为空间域x或y方向计算范围的最大值,tmin为空间域x或y方向计算范围的最小值.

在求得正波数采样范围后,可根据频谱能量分布总结出波数选取的规律.本文总结波数选取规律的具体准则为:频谱能量大且变化剧烈的区间加密采样,频谱能量小且变化缓慢的区间稀疏采样.

1.3 CPU-GPU并行理论方法

本文提出的基于任意傅里叶变换的空间-波数域三维重力异常正演算法中,采用任意傅里叶变换计算时不同波数下离散单元积分相互独立,不同波数下求解五对角方程组相互独立,这两个关键过程均具有良好的并行性.本文采用OpenMP并行实现追赶法求解五对角方程组,采用GPU并行实现正、反二维傅里叶变换过程,实现整体算法的CPU-GPU并行加速.下面具体介绍这两个并行理论和结构.

每个波数需进行方程组求解,在求解五对角方程组时,追赶法算法虽然计算量小,但存在大量循环和迭代运算,计算复杂,GPU相对于CPU控制单元数量少,指令控制能力差,且GPU适用于大量的轻量级运算(巴振宁等,2022),追赶法算法存在复杂的指令流控制和复杂的公式计算,因此将五对角方程追赶法求解计算在CPU上采用OpenMP并行计算,并行过程如图1所示:

图1 OpenMP并行机制

如图所示,主线程开始运行,分配多个子线程执行并行计算任务,主线程等待子线程完成所有的并行计算任务,然后继续后续工作(蔡佳佳等,2007).OpenMP并行有丰富的指令,易于实现,算法改造简单高效(刘凯和寇正,2003).

相对于CPU,GPU可以同时开辟成千上万个线程,且存储器读写效率更高,在NIVIDIA CUDA编程框架中,将大规模的简单数据计算分配到GPU线程上并行执行,能有效地提升计算速度.本文中的基于二次插值形函数的任意傅里叶变换算法计算过程主要以乘法和加法为主,且每个节点的傅里叶变换之间相互独立,适用于GPU并行计算.下面具体介绍GPU并行方案.

以二维形函数傅里叶变换正变换为例,将空间域x和y方向离散为Nx×Ny个节点,节点的积分系数提前算出并存储,剩下的计算分为两步:①如图2所示,先对每个波数下f(x,y)沿x方向做Nx次乘法和加法,得到Fx(kx,y);②再对Fx(kx,y)沿y方向做Ny次乘法和加法得到F(kx,ky),得到该波数下的频谱值.若波数选取总数为Nkx×Nky,模型垂向剖分为Nz层,则算法中傅里叶正变换所需要加法和乘法的计算次数均为:Nz×(Ny×Nkx×Nx+Nkx×Nky×Ny).由于不同波数之间的傅里叶变换积分相互独立,可以将外面三层循环(Nz×Ny×Nkx或Nz×Nkx×Nky)分配给GPU线程并行计算,每个GPU线程仅负责一个波数的积分运算:Nx或Ny次乘法和加法运算.

图2 x方向一维积分计算过程

GPU并行部分称为核函数,CPU上启动GPU上执行,本文采用的GPU通用技术通过线程网格grid以及线程块block来组织核函数并行计算部分,grid以及block有三个方向参数:x,y,z.常用的线程层次有一维层次(一维线程块与一维线程网格)、二维层次(二维线程块与二维线程网格)和三维层次(三维线程块与三维线程网格)(董廷星等,2009;贾格等,2017).

以二维线程层次为例,如图3所示,每个线程有各自的核函数计算任务,二维线程层次中线程通过(threadIdx%x,threadIdx%y)来定位自己在线程块中的索引,线程块通过(blockIdx%x,blockIdx%y)来定位自己在线程网格中的索引,两个索引准确指向线程数据对应的逻辑位置,实现并行部分和主程序的对接.

图3 二维线程层次结构

图3表示f(x,y)沿x方向做傅里叶变换积分得到Fx(kx,y)的过程.从图3中可以看出,每一个线程块中有a×b个线程,线程网格中有m×n个线程块,线程块中的一个GPU线程负责一个波数的积分计算,因此有m=(a+Nkx-1)/a,n=(b+Ny-1)/b,Nkx、Ny分别为沿x方向积分中kx和y方向网格剖分节点数.一维层次中,每一个线程块中有a个线程,线程网格中有m个线程块,有m=(a+Nkx×Ny-1)/a.三维层次增加了z方向的维度,用来计算不同z平面的任意傅里叶变换积分,每一个线程块中有a×b×c个线程,线程网格中有m×n×k个线程块,有m=(a+Nkx-1)/a,n=(b+Ny-1)/b,k=(z+Nz-1)/c,Nz为z方向节点个数.

2 数值算例

本节主要介绍任意傅里叶变换在重力正演时的波数采样规则,验证算法的正确性与效率.测试所用PC参数为CPU Intel(R) Core(TM) i9-9980XE,主频3.0 GHZ(18核),128 GB RAM.GPU显卡型号NVIDIA TITAN RTX,显存24G,计算能力7.5,CUDA版本号11.6,基于Linux编译环境.

2.1 正确性验证

引入相对均方根误差(RRMS)来研究基于任意傅里叶变换的重力异常数值模拟精度,当RRMS<1%时,即认为精度满足要求.计算公式(Wu,2016)如下:

(18)

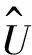
设计棱柱体模型,计算区域范围20 km(x)×20 km(y)×7.5 km(z),异常体水平方向上位于模拟区域中心,顶面埋深为0.5 km,大小为8 km(x)×8 km(y)×2 km(z),异常体密度为2000 kg·m-3.剖分节点个数为251(x)×251(y)×151(z),三个方向上均匀剖分,水平方向网格间距均为80 m,垂直方向为50 m.

根据1.2节总结的采样规则,本节模型选取kx和ky波数相同,基频大小均为Δk=3.14×10-4,波数最大值为3.9×10-2,在频谱能量变化剧烈的区间进行加密,加密范围为前三个基频区间:1×10-5～9×10-4,选取25个波数,其他区间均匀分布,正负波数选取181×181个.将三维重力异常全息傅数值模拟异常体内部(z=0 m)、异常体外部(z=500 m)结果与解析解对比.

图4为重力异常场在地面z=0 m和异常体内部z=500 m数值解与解析解的平面等值线图.由图可知,两个平面上数值解和解析解等值线图重合,场值吻合得很好,且在z=0 m平面gx、gy以及gz三个分量的相对均方根误差分别为0.48%,0.48%,0.52%,z=500 m平面gx、gy以及gz三个分量的相对均方根误差分别为0.61%,0.61%,0.65%,异常体内部和外部的重力异常场的相对均方根误差均小于1%,表明基于任意傅里叶变换的空间-波数域三维重力异常算法正确,波数选取规则对异常体内外部的场均适用.

图4 重力异常场数值解与解析解等值线图

2.2 计算精度与计算效率

设计连续密度模型,研究基于任意傅里叶变换空间-波数域三维重力异常算法的计算效率与精度.文献表明(吴乐园,2014;Dai et al.,2018)Gauss-FFT法对频率域重力异常数值模拟具有非常高的精度,本节以高斯点数NG=4的高斯快速傅里叶变换的空间-波数域重力异常场数值模拟结果(Dai et al.,2018)作为连续介质的参考解.研究本文算法基于不同波数个数的计算精度和计算效率,算法在CPU上串行计算.

连续密度模型垂直方向密度不变,在水平方向上密度变化可表示为

ρ=2000×e-6×10-8(x2+y2).

(19)

模拟区域范围为20 km(x)×20 km(y)×7.5 km(z).异常体区域大小为20 km(x)×20 km(y)×2 km(z),顶面埋深为0.5 km.区域剖分节点个数为:201(x)×201(y)×151(z),水平方向网格间距均为100 m,垂直方向50 m.kx和ky的波数范围为-3.14×10-2～3.14×10-2,基频大小均为3.14×10-4,波数个数变化如表1所示.

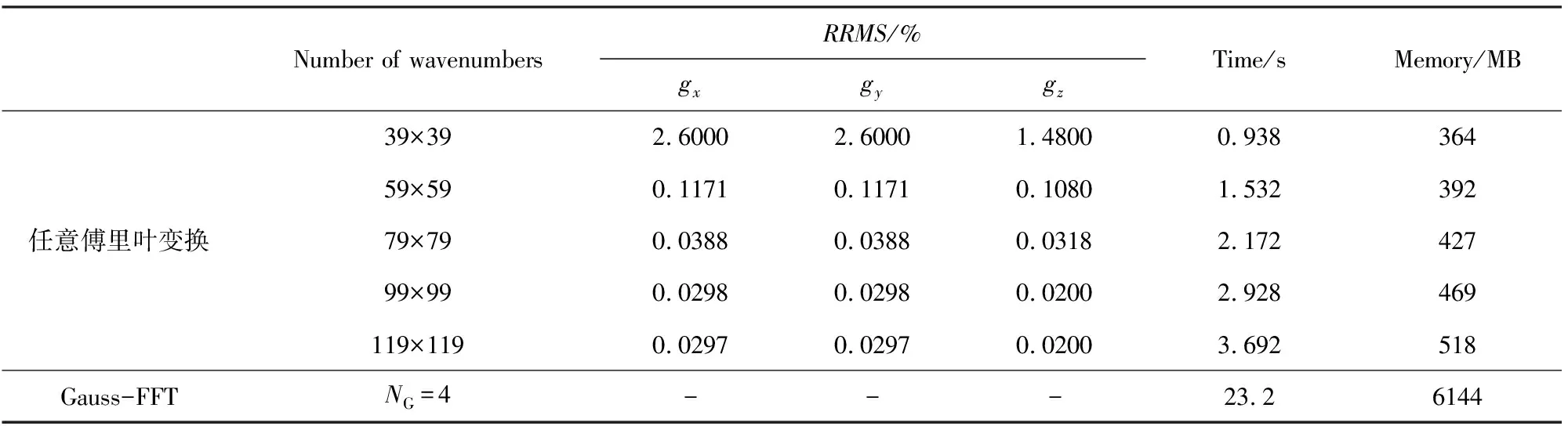
表1 任意傅里叶变换与高斯快速傅里叶变换计算精度与计算效率对比

采用任意傅里叶变换算法进行数值模拟,表1为任意傅里叶变换和Gauss-FFT空间-波数域重力异常正演计算精度和计算效率对比表.表中统计了不同波数个数下:地面z=0 m重力场的相对均方根误差、整个区域计算耗时和内存占用.从表中可以看出,①随着波数增多,重力异常场三个分量的RRMS逐渐减少,基于任意傅里叶变换的空间-波数域算法正演耗时增多,内存占用也增多,当波数大于99×99时,相对均方根误差基本不变;②波数选取个数为99×99时,以Gauss-FFT的数值解为参照,任意傅里叶变换正演得到gx、gy、gz三分量的RRMS分别为0.0298%,0.0298%和0.02%,与Gauss-FFT数值解结果非常接近;③模型剖分节点为201×201×151、计算节点数为201×201×151时,任意傅里叶变换计算耗时约3 s,占用内存约469 MB,Gauss-FFT法耗时23 s,占用内存约6144 MB,相比于Gauss-FFT,任意傅里叶变换算法效率提高了约8倍.

图5是波数为99×99时任意傅里叶变换与Gauss-FFT两种数值解的重力异常场z=0 m、z=500 m平面等值线图.从图中可以看出,异常体内外部两者结果基本吻合,表明本文算法对连续模型适应强且计算效率高.

图5 重力异常场任意傅里叶变换数值解与高斯数值解等值线图

3 CPU-GPU并行加速

通过1.3节分析,并行加速有两部分:第一部分:五对角方程组求解;第二部分:二维任意傅里叶正、反变换.采用2.2节中的模型,该模型已验证精度,改变计算节点数,对比不同GPU线程层次加速任意傅里叶变换效率;使用多核CPU、GPU分别加速五对角方程组求解与任意傅里叶变换,改变计算节点数,对比CPU与GPU的加速比.

3.1 GPU线程层次加速对比

一维层次、二维层次以及三维层次GPU结构加速任意傅里叶变换,同时使用culbas库直接加速任意傅里叶变换.保持z方向节点数为151,改变水平方向计算节点个数,波数个数与空间域节点数保持一致,对比四种GPU方法加速任意傅里叶变换的计算时间以及GPU显存-CPU内存传输时间,结果如表2所示.

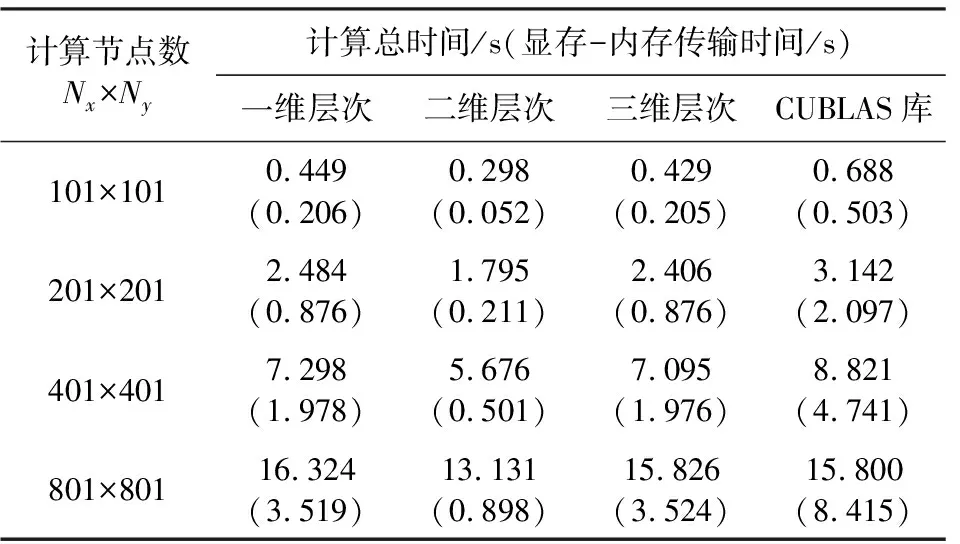
表2 不同GPU方法加速任意傅里叶变换计算时间

从表中可以看出,不同计算节点个数下,一维、二维、三维层次的计算时间相近,但是二维层次的显存-内存传输耗时最少,二维层次下的计算总时间少于一维和三维层次的计算总时间,同时一维、二维、三维的计算总时间优于CUBLAS库.因此,任意傅里叶变换GPU加速方案采用二维层次.

3.2 CPU、GPU加速方案对比

针对并行加速两部分,分别采用CPU单核、18核CPU以及GPU进行数值模拟,保持z方向节点数为151,改变水平方向计算节点个数,波数个数与空间域节点数保持一致,对比不同加速方法的加速比,CPU、GPU并行加速五对角方程组求解时间如表3所示.

表3 CPU、GPU加速五对角方程组计算时间

从表中可以看出,五对角方程组求解过程中,CPU加速效果好于GPU加速,这是因为每个波数下的五对角方程组求解过程复杂,并不是简单的点对点简单运算,随着计算节点数增加,加速比最高可达13.6,因此,采用CPU加速五对角方程组求解.

CPU、GPU并行加速任意傅里叶变换时间如表4所示.

表4 CPU、GPU加速任意傅里叶变换计算时间

从表中可以看出,任意傅里叶变换时间占整个计算过程的90%,计算节点较少时,CPU加速效果优于GPU加速,这是因为计算量小,GPU处理性能并没有体现出来(陈召曦等,2012),随着计算节点数的增加,18核的CPU加速比最高达到12.59,GPU的加速比越来越大,最高达到48.77,CPU线程核数与加速比并不是线性关系,这是因为OpenMP并行时不同线程间数据存在依赖关系,线程同步、线程调度消耗时间,而GPU拥有众多计算单元,每个GPU线程负责一个波数的积分运算,随着计算节点的增加,加速比也会越来越大,GPU加速效果优于CPU加速.

因此本文采用OpenMP并行实现追赶法求解五对角方程组,采用二维层次GPU并行实现二维任意傅里叶正、反变换,实现整体算法的CPU-GPU并行加速方案.

4 实际地形应用

长白山火山地区具有丰富的地热资源.基于长白山火山区域的DEM数字高程数据(经度为127°E至129°E,纬度为41°N至43°N)设计实际地形应用模型,采用基于任意傅里叶变换的空间-波数域重力异常正演CPU-GPU并行算法进行数值模拟.地形数据如图6所示,图中黑框内的范围为目标区域,范围为100×100 km,其他区域为扩边区域,总体范围为200×200 km.为了将地形描述清楚,在地形起伏大的目标区域(x方向范围:-20～20 km,y方向范围:-20～20 km)采用100 m网格间距,其他区域采用500 m网格间距.海拔最高为2727 m,最低为257 m.z方向向下为正,z方向范围-4～4 km,-4～0 km垂直方向网格大小为10 m,0～4 km网格大小为200 m,模拟区域节点个数为721(x)×721(y) ×421(z),密度设为常密度,数值为2580 kg·m-3.

图6 长白山火山区域地形图

根据1.2节中的波数选取规律,本节模型选取的kx和ky波数相同,两个方向上基频大小均为Δk=3.14×10-5,波数最大值为3.14×10-2,在前10个基频1×10-6～3×10-4进行波数加密,选取201×201、401×401两种波数进行数值模拟.将起伏地形看成721×721个密度为2580 kg·m-3的常密度棱柱体模型组成,可近似求得起伏地形重力异常的解析解,z=-4 km为观测面.

对整个区域进行数值模拟,区域节点个数为721×721×421,计算节点个数为521×521×421.当波数个数为201×201时,CPU串行计算时间为171.62 s,占用内存为12.3 G,CPU-GPU并行计算时间为7.81 s,CPU+GPU占用内存为12.3 G+215 MB,加速比为22,z=-4 km重力场三分量的RRMS为0.34%,0.33%,0.11%;波数个数为401×401时,CPU串行计算时间为470 s,占用内存为17.3 G,CPU-GPU并行计算时间为17.68 s,CPU+GPU占用内存为17.3G+276 MB,加速比为26.5,z=-4 km重力场三分量的RRMS为0.0063%,0.0063%,0.0035%.图7为观测面z=-4 km上波数选取401×401的重力异常场gx、gy以及gz三分量数值解和解析解对比图,从图中可以看出,数值模拟与解析解计算结果形态相似.

图7 实际地形重力异常场数值解以及解析解结果

为了对比本文算法计算精度,采用NG=4的Gauss-FFT方法(Dai et al.,2018)进行数值模拟,CPU串行计算时间为6234.23 s,占用内存为113.75 G,与解析解对比,z=-4 km重力场三分量的RRMS为0.035%,0.035%,0.017%,当任意傅里叶变换的波数选取个数为401×401时,本文算法的计算精度高于NG=4的Gauss-FFT计算精度,计算时间仅需17.68 s,适用于复杂条件下重力模型计算.

综上,计算结果证明本文算法及加速方案适用于大规模起伏地形模型的计算,证明1.2节中总结的波数选取规律也适用于空间域非均匀采样,且基于CPU-GPU加速方案的计算时间比单核CPU计算时间快26倍.