基于岩石力学的井周裂缝流体疏导性分析与产能评价
2024-02-03张翰林苏远大唐晓明
张翰林,苏远大,王 淼,唐晓明
(1.中国石油大学(华东)地球科学与技术学院,山东青岛266580;2.中海石油(中国)有限公司天津分公司,天津300459)
由于全球能源需求急速增长,非常规油气藏逐渐成为国内外勘探开发的重要领域之一。其中,裂缝性油气藏的产量与储量在非常规油气资源中占有较大比重,该类油气藏是以裂缝为主要储集空间与渗流通道的油气藏,储集层通常具有岩性致密、低孔低渗和结构复杂等特点,因此裂缝的流体疏导性能是决定储层产能高低的重要因素。
国际上已有对于裂缝流体疏导性能及相关产能评价方法的研究,BARTON等[1]提出了临界应力断层理论,利用地应力与裂缝几何形态以及温度测井研究断层的水力传导状态。ZOBACK等[2]利用三维应力莫尔圆分析了水力压裂过程中孔隙压力增加有助于诱发裂缝的开启;KRUSZEWSKI等[3]利用三维应力莫尔圆确定储层接近临界应力状态的优势通道。近几年,国内一些学者也开展了相关研究工作,陆云龙等[4]利用电成像提取的井壁裂缝结合三维莫尔圆开展了裂缝有效性分析工作。李思亦等[5]引入声波远探测识别裂缝并研究了不同地区碳酸盐岩储层裂缝的有效性。徐珂等[6]通过建立裂缝参数与产能的关系发现裂缝面应力状态与产能有较好的相关性。
本文基于电成像测井技术与近年发展起来的偶极横波远探测技术[7-8]分别获取井周从井壁到远井的裂缝信息,结合岩石力学方法计算裂缝的应力状态并分析井周裂缝流体疏导性能,将上述方法应用于渤海地区潜山裂缝性油气藏的产能评价中,验证了方法的有效性。
1 地应力分析
1.1 地应力方向
在钻井的过程中,随着井筒中岩心的取出,井孔周围的应力会发生变化,井孔周围的环向应力分布可由Kirsch方程描述[9],即:
(1)
式中:σβ为井壁周围的环向应力;σH和σh分别代表地层最大水平主应力与最小水平主应力;R为井眼半径;r为距离井眼中心的径向距离;β为径向r与最大水平主应力方向的夹角;p为井中流体压力。令σH=40MPa,σh=30MPa,p=30MPa,R=0.1m。
根据(1)式计算得出井孔附近地层环向应力随径向距离变化的分布特征(图1),可以明显发现井孔周围产生应力集中现象,并且受应力方位与径向距离的影响较大。由于存在井孔应力集中现象,在最大水平主应力方向,井壁易进入拉伸状态,同时岩石抗拉强度较低,易形成钻井诱导产生的诱导缝,所以,利用井壁诱导缝的走向可指示最大水平主应力方向[10]。
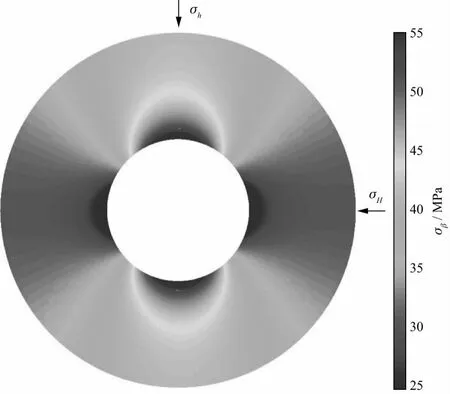
图1 井壁附近环向应力分布
通常诱导缝在井壁上发育数量多且方位不完全相同。因此,可以利用Fisher统计法计算诱导缝的平均方向,并基于诱导拉伸裂缝的质量评价标准(表1)判断其数据质量的可靠性[11]。其定义为:

表1 诱导拉伸裂缝的质量评价体系
(2)
(3)
(4)
式中:ωi为第i条井壁诱导缝的走向。
诱导缝的平均方位可表示为:
(5)
1.2 地应力大小
通常,地层岩石受垂向应力、最大水平主应力、最小水平主应力以及岩石内部的孔隙压力作用,其中,垂向应力主要来自于上覆岩层的重力作用,可由密度测井资料计算得到。而水平方向上主应力除了来自地层垂向应力的作用,还受构造运动的强烈影响。
针对我国渤海湾盆地渤中19-6区块深层的裂缝性潜山凝析气田开展评价分析,由于该区域主控构造为走滑断层,且构造区域内地应力表现为:最大水平主应力>垂向应力>最小水平主应力。因此,在众多水平地应力计算模型中我们采用适用于该区块构造情况的黄氏模型进行计算[12-13],该区块地应力计算公式为:
(6)
式中:σV,σH,σh分别为地层的垂向应力、最大水平主应力与最小水平主应力;g为重力加速度;h0,h为井段起始深度与终止深度;ρave为上覆岩层的平均密度;ρ为岩石的体积密度;v为泊松比;α为Biot系数;Pp为孔隙压力;βH,βh为地区构造应力系数。
2 裂缝流体疏导性分析
2.1 裂缝应力状态分析
三维应力莫尔圆是岩石力学中分析裂缝面应力状态的一种常用工具[8],在给定3个主应力(σH,σh,σV)和地层孔隙压力Pp的情况下,地层岩石的有效主应力可表示为:
(7)
主应力的3个正交方向形成如图2a所示的笛卡尔坐标系,裂缝在该坐标系中的方位或其法线方向决定了裂缝面的应力状态,裂缝面的法向单位向量n为:
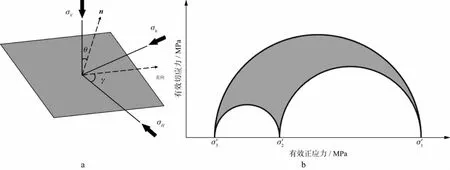
图2 裂缝的应力状态a 裂缝面的三轴应力状态示意; b 三维应力莫尔圆
n=(sinθsinγ,sinθcosγ,cosθ)T
(8)
式中:γ是裂缝走向相对于σH的方位夹角;θ是裂缝的倾角;T表示转置。在裂缝的法线方向上,裂缝面的有效正应力为:
σn=sin2θ(σ′Hsin2γ+σ′hcos2γ)+σ′Vcos2θ
(9)
那么,裂缝面的切应力为:
τn=
(10)
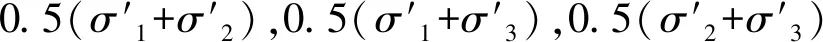
在确定地应力大小和方位的情况下,可针对不同产状裂缝利用三维应力莫尔圆展开应力状态分析。对于井壁裂缝可利用电成像测井方法识别并准确拾取产状;针对远井裂缝则可通过偶极横波远探测方法来识别,下面对远井裂缝产状的拾取展开讨论。
偶极横波远探测成像采用方位角旋转的方法从四分量偶极声波数据中得到裂缝的方位角,其中,SH横波数据是由一个偏振角度为φ的四分量数据所构造[14-15]:
SH(φ)=xxcos2φ-sinφcosφ(xy+yx)+
yysin2φ
(11)
当SH横波偏振角度与裂缝走向方向一致时,裂缝的SH波反射强度最大,因此,SH波振幅最大时的角度φ0即为裂缝走向角。沿着方位角φ0的方向成像,可以得到裂缝的二维图像,并从中可以确定裂缝到井眼的距离以及裂缝的倾角θ。故利用偶极横波远探测成像可以拾取远井裂缝的产状。
然而,在使用(11)式确定方位时,存在固有的180°不确定性,即φ0和φ0+180°同为该公式的解。因此,需要讨论偶极横波远探测成像中180°不确定性对于裂缝应力分析的影响。由于φ在等式中以sin2φ和cos2φ的形式出现时产生的应力对是一个以180°为周期的函数。换言之,在(9)式和(10)式中,代入裂缝倾角θ,裂缝走向方位角φ0和φ0+180°会产生同样的(σn,τn)值,所以,这种不确定性并不影响裂缝应力状态的计算。上述分析的重要意义在于,可以用偶极横波远探测成像拾取远井裂缝的产状,并且裂缝在偶极横波远探测成像中的180°不确定性并不会影响裂缝面应力状态的确定。因此,岩石力学中的三维应力莫尔圆与电成像测井技术、偶极横波远探测技术可以有效结合起来计算井周裂缝的应力状态。
2.2 裂缝的临界应力状态判别
基于裂缝应力状态的莫尔圆分析,可以结合莫尔-库仑破裂准则进行裂缝临界应力状态判别表征裂缝流体疏导性[1],对于利用(9)式和(10)式得到的应力对(σn,τn),该准则为:
τn=S0+μσn
(12)
式中:S0是岩石的内聚力;μ是摩擦系数。
对于裂缝性岩石,S0常可忽略,于是,(12)式与Byerlee的摩擦定律相似且0.6≤μ≤1[16],在三维应力莫尔圆上绘制莫尔-库仑破裂准则线,将裂缝面应力状态的二维图形划分为两部分,如图3所示。在μ=0.6这条破裂线附近及以上的阴影区域定义为临界应力区域,在该区域内,裂缝被激活并容易开启或发生滑移,具有良好的流体疏导特性。在破裂准则线以下的区域,裂缝通常处于不活跃或封闭的状态,其流体疏导性能较差,难以作为有效的油气渗流通道。

图3 莫尔-库仑破裂准则下的三维应力莫尔圆
2.3 不同地应力状态与孔隙压力的模拟
由(9)式和(10)式可知,裂缝面的应力对(σn,τn)不仅取决于裂缝方位角γ和θ,同时也受地应力状态的影响,所以需要注意的是,根据表2所示的Anderson相对地应力大小和断层分类模式可以确定地应力相对大小关系[17]。其中,σ1,σ2,σ3分别表示最大地应力、中间地应力和最小地应力,地应力状态强烈控制着临界应力状态(σn,τn)在莫尔圆中的分布位置[18]。

表2 Anderson断层应力分类
基于理论计算说明这种影响,设σ1,σ2,σ3的应力值分别为70,50,40MPa,孔隙压力为30MPa,令这3个地应力值按表2分别交替赋值于3个主应力(σH,σh,σV)来模拟正断层、走滑断层和逆断层的应力状态。
对于正断层类型(σV>σH>σh,图4a左侧),图4a 右侧模拟结果显示莫尔圆中裂缝的方位角γ以顺时针方向从0°逐渐增加至90°,倾角θ以逆时针方向从0°逐渐增加至90°,红色区域代表裂缝的临界应力状态表明,裂缝的方位角γ处于较小到中等范围并且倾角θ为中到高倾角时趋于临界应力状态,此时裂缝具有较强的流体疏导性能;对于走滑断层类型(σH>σV>σh,图4b左侧),图4b右侧模拟结果显示,莫尔圆中裂缝的方位角γ以顺时针方向从0°逐渐增加至90°,倾角θ以逆时针方向从0°逐渐增加至90°,红色区域代表裂缝的临界应力状态表明裂缝的方位角γ处于较小到中等范围并且倾角θ为高倾角时趋于临界应力状态,此时裂缝具有较强的流体疏导性能;对于逆断层类型(σH>σh>σV,图4c左侧),图4c 右侧模拟结果显示,莫尔圆中裂缝的方位角γ以顺时针方向从0°逐渐增加至90°,倾角θ同样以顺时针方向从0°逐渐增加至90°,红色区域代表裂缝的临界应力状态表明,裂缝的方位角γ处于中等到高的范围并且倾角θ为低到中等倾角时趋于临界应力状态,此时裂缝具有较强的流体疏导性能。

图4 不同断层地应力作用下的莫尔圆临界应力状态区域模拟a 正断层; b 走滑断层; c 逆断层
根据(7)式可知,有效地应力大小取决于地应力与孔隙压力大小,因此在给定地应力大小的情况下,地层孔隙压力Pp的大小对于临界应力状态区域的分布起着重要的作用。以图4b走滑断层类型为例(最大水平主应力、最小水平主应力、垂向应力分别为70,50,40MPa),令孔隙压力大小分别取25,30,35MPa模拟孔隙压力变化对于裂缝流体疏导性能的影响。由图5的模拟结果发现,若孔隙压力较小,无论裂缝产状是否为优势破裂情况,裂缝都处于较稳定的状态不易发生破裂,故流体疏导性能较差,随着孔隙压力的不断增加,裂缝临界应力状态可包含的裂缝产状范围逐渐增加,裂缝更易于发生破裂,裂缝的流体疏导能力也逐渐增强。
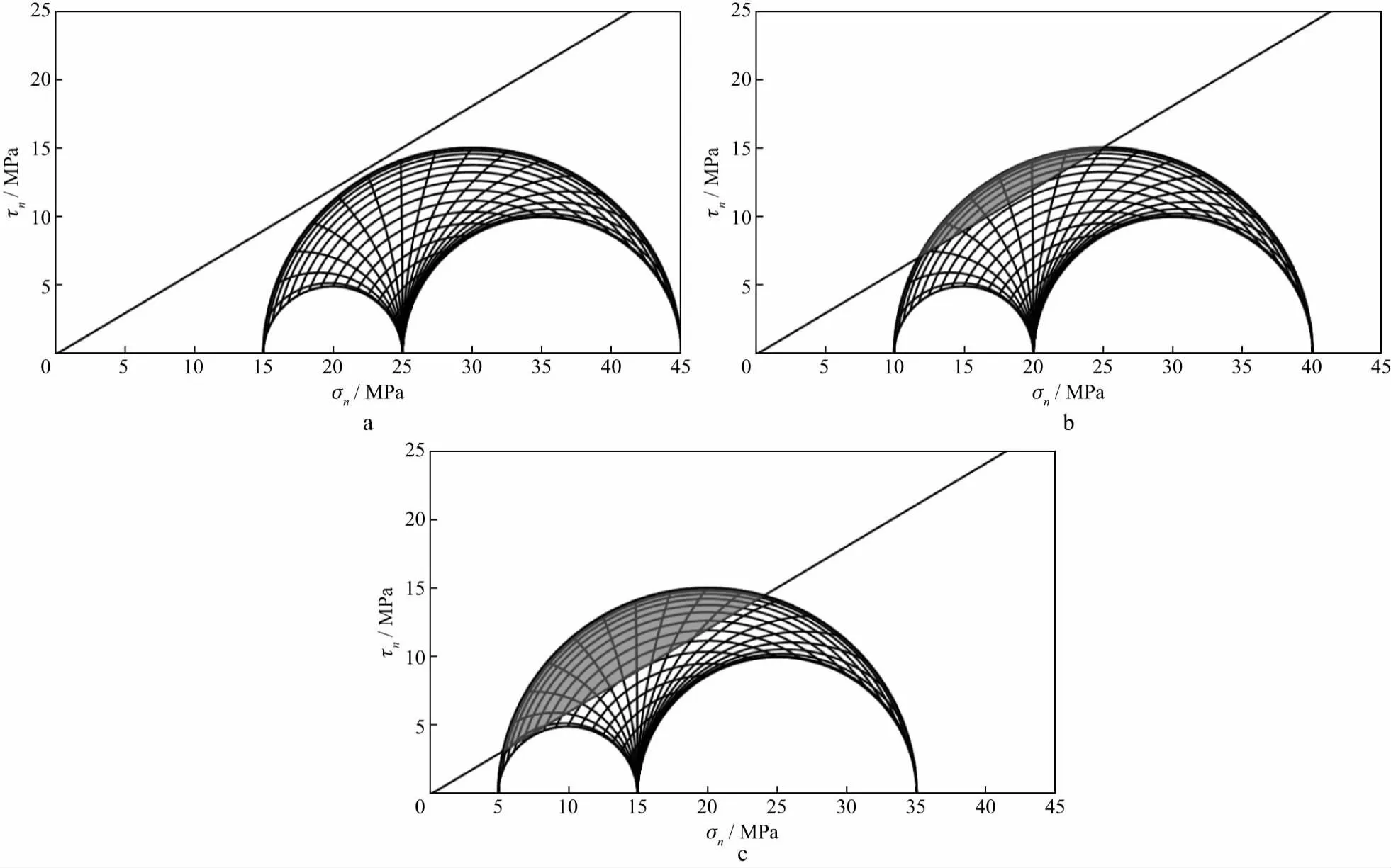
图5 不同孔隙压力的莫尔圆临界应力状态区域模拟a 25MPa; b 30MPa; c 35MPa
因此随着裂缝性油气藏开发过程的进行,地层孔隙压力不断下降会导致裂缝趋向闭合,此时可作为油气输运通道的裂缝数量将减少从而导致产能降低;在实施水力压裂或者注水开发的过程中,孔隙压力随着压裂液或注水量的增加而增大,之前不易发生破裂的裂缝产状也会逐渐达到临界应力状态,裂缝的流体疏导性能增加,产能也将大幅提高。
以上模拟实例清楚地表明,只有将测井得到的裂缝方位信息准确地与实际地应力状态和孔隙压力情况相结合,才能正确地表征井周裂缝是否具有流体疏导性能的临界应力状态。
2.4 井周裂缝流体疏导性的定量评价
利用莫尔圆分析裂缝流体疏导能力的思路,提出一种基于岩石力学定量评价井周裂缝流体疏导能力的方法。由于临界应力状态下的裂缝具有较好的疏导能力,同时裂缝面的内聚力非常小,可忽略不计。所以,根据(12)式,可以利用摩擦系数,即裂缝面的切应力与正应力之比,作为定量反映裂缝流体疏导性的重要指标[19],即:
(13)
摩擦系数的大小可以评价裂缝流体渗流能力的强弱,但裂缝流体疏导性能与摩擦系数并非线性关系。因此,引入一个经验系数a对摩擦系数进行校正,使得校正后的摩擦系数可准确地定量反映裂缝流体疏导性能,即:
(14)
3 实例分析
3.1 区域地质背景
渤中凹陷位于渤海湾盆地的东部渤海海域。其中,研究目标区块渤中19-6构造区位于渤中凹陷西南部的深层构造脊上,渤中19-6构造区经历了多期构造运动,早印支运动、晚印支运动与燕山运动对太古界变质岩潜山的形成及裂缝的发育起关键作用[20-22]。由于该区块储层基质表现为特低孔和特低渗特征,因此,裂缝为渤中19-6析气田深层潜山储层的主要储集空间与渗流通道[23]。但裂缝性潜山岩性复杂且储层非均质性强,井与井之间测试产能差异大,储层产出能力评价面临挑战。
3.2 X井的井周裂缝流体疏导性分析
X井目标层段是该区块典型的变质岩裂缝性储层,其产能主要依靠于地层中发育的裂缝网络贡献。图6中,第1道是自然伽马曲线;第2道为深度;第3道是对四分量交叉偶极声波数据进行处理后的偶极方位各向异性,其各向异性大小的变化范围为1%~5%;第4道的各向异性方位变化表明,该层段各向异性是不同方位的多组裂缝交叉作用的结果;经过偶极横波远探测成像探测到两条过井大裂缝,分别在N80°E/S80°W(第5道)和E50°S/W50°N(第6道)方位获得最佳成像结果。成像图显示,井眼附近径向深度25m范围内的几个主要的高角度(60°~80°)的裂缝。在这两个方位的大裂缝与井眼相交的5m内,远探测成像结果在图6最右侧的电成像测井中得到验证。除了大量的低角度裂缝外,电成像图像中的高角度裂缝显示出与远探测成像中的高角度裂缝方位一致。电成像图还显示高角度裂缝存在近乎相反的倾向,但是由于前面所提到的偶极横波远探测的180°不确定性,这种倾向相反的差异在第5道与第6道的远探测成像图中无法探测到。然而,这种不确定性并不影响利用三维莫尔圆来计算裂缝面的应力状态。

图6 X井过井大裂缝的偶极横波远探测成像与过井处电成像结果
井壁电成像测井结果显示,该井在太古界潜山段(累计厚度为445.3m)共拾取诱导缝65条,利用(2)式至(5)式求取最大水平主应力方向为89.5°,标准差为11.4°。根据表1质量分级标准为A,因此该最大水平主应力方向的计算结果有较高可靠性。根据(6)式计算可得地层的最大水平主应力为144MPa;最小水平主应力为80MPa;垂向应力为109MPa;地层孔隙压力测试值为67.5Mpa。根据表2的Anderson分类标准,该储层具有与图4b相似的走滑断层所对应的地应力状态,利用(9)式与(10)式计算该段井壁以及远井裂缝的应力状态,并通过(12)式判断临界应力状态区域,三维应力莫尔圆分析结果如图7所示。
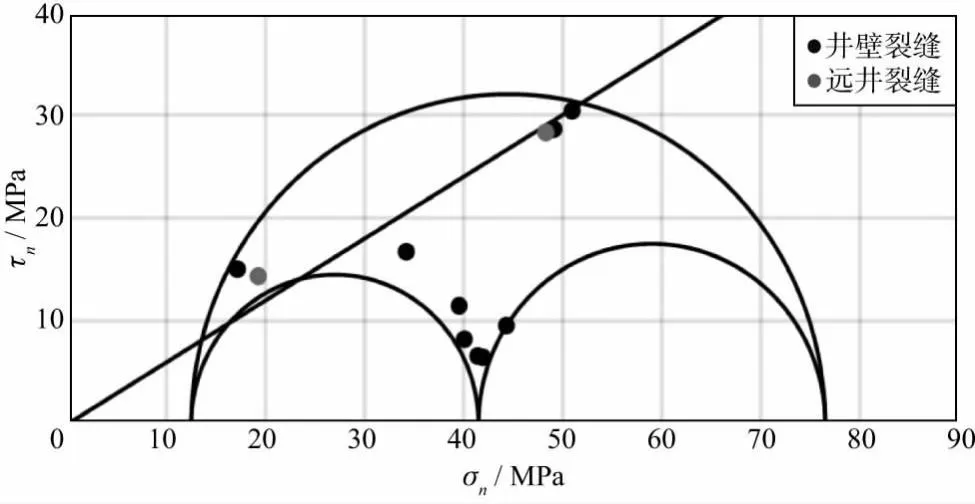
图7 X井大裂缝过井处裂缝群在三维莫尔圆上分布的分析结果
特别值得注意的是,分析结果表明图7中所示的位于两个不同方位的大尺度过井裂缝(红点)均处于临界应力区域。对于井壁电成像图中拾取的井壁裂缝(黑点),只有高角度裂缝处于临界应力状态,这意味着该储层的产量主要来自于高倾角裂缝的贡献,而非低角度裂缝,与图4b的模拟结果一致,特别是由于裂缝相交段位于储层段内,从远探测成像图中可以清楚地看到裂缝在地层中的延伸,清晰地指示了储层油气的输送通道,为油田开发生产的规划提供了有效信息。
3.3 用裂缝疏导性能解释不同井之间的产能差异
渤中19-6区块A井中的4043.40~4142.00m段,B井的3879.00~3998.66m段和C井的4411.00~4499.80m段同处于渤中19-6区块中的变质岩潜山段,且均为裂缝发育层段,分别发育裂缝54,35,92条,对这3个层段中的所有裂缝利用(9)式和(10)式进行应力状态计算,对计算结果进行分析得到如图8所示τn-σn应力状态分布。

图8 A,B,C井裂缝发育段的裂缝应力状态分析
基于图8中3个裂缝发育层段的裂缝应力状态结果可得出初步结论:A井裂缝段中大部分裂缝位于破裂准则线之下,处于非临界应力状态区域,可以作为油气运移通道的裂缝数量较少,故裂缝流体疏导性能较弱;B井与C井在裂缝段中位于破裂准则线以上或破裂线附近的裂缝较多,处于临界应力状态,故多数裂缝趋于开启或错动,有着较强的流体疏导性能,但C井裂缝段的裂缝密度明显大于B井,因此预测C井产能也将高于B井,A井产能最低。
为了得到更加准确的分析结果,通过(14)式计算校正后的裂缝摩擦系数并加权到裂缝密度中[24],然后使其沿着测试层段深度进行积分,构造一个针对于整个裂缝发育层段流体疏导性能的定量评价指数F,即:
(15)
式中:e为裂缝密度;h0和h分别为裂缝测试层段起始深度与终止深度。
计算得出A井、B井与C井裂缝发育层段的流体疏导性能评价指数F分别为5.0,13.4和33.1。表3为对应的地层测试结果。可以发现,其产气量与计算的评价指数F值有较好的相关性(图9)。产能预测是一项需要综合考虑多种因素的难题,这一结果不仅验证了从岩石力学角度评价裂缝流体疏导性的合理性与有效性,也为裂缝性油气藏产能评价提供了可靠的方法,同时解决了该区块凝析气田太古界潜山储层不同井之间产能差异大的难题,可为油田现场试油与开采方案的制定提供合理的依据。
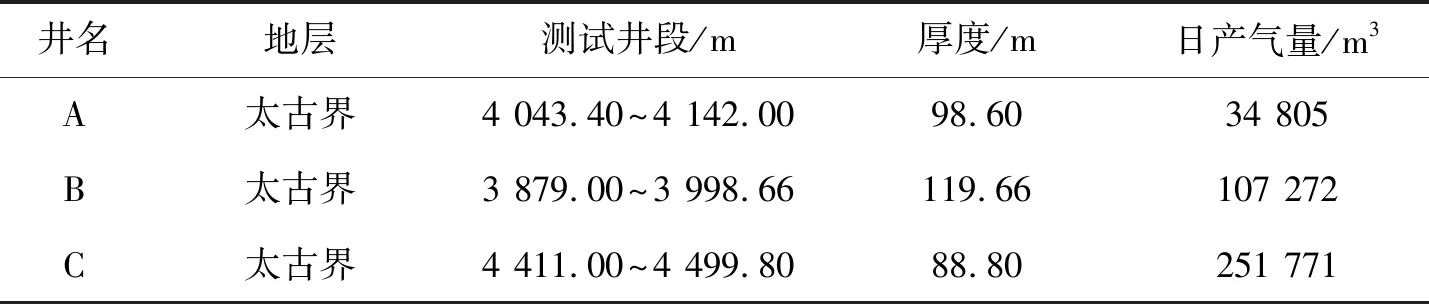
表3 A,B和C井地层测试结果

图9 A,B,C井测试层段产能与流体疏导性能评价指数F值
4 结论
1) 将电成像测井技术、偶极横波远探测技术所拾取的井周裂缝与岩石力学分析相结合,形成了井周从井壁到远井范围内裂缝的流体疏导性能分析方法,并且利用校正后的摩擦系数可以完成定量评价,实现对裂缝性储层的产能评估与预测。
2) 基于模拟不同断层类型下地应力状态与孔隙压力大小的临界应力状态区域表明,除裂缝的方位外,地应力状态与孔隙压力大小对于评价裂缝是否处于临界应力状态相当重要。
3) 在非均质性强且基质低孔低渗的裂缝性潜山储层产能评价中的应用表明,本文建立的裂缝流体疏导性分析与产能评价方法有效且可靠,能够为油田的高效开发提供依据与有效指导。
