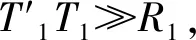典型水深与海底介质条件下的OBC/OBN多分量地震数据波型特征
2024-02-03王腾飞刘学义程玖兵
王腾飞,刘学义,程玖兵
(同济大学海洋地质国家重点实验室,上海200092)
近年来,随着海洋油气勘探开发不断深入,勘探目标逐步从构造油气藏向隐伏岩性、构造-岩性复合油气藏拓展,勘探难度不断提高,对构造成像、岩性区分与油气预测精度提出了更高要求。常规海面拖缆采集由于缆线长度有限、无法采集横波信号等缺点,在解决上述一系列问题时存在明显不足。随着地震观测技术的不断完善,海底多分量地震采集成本大幅降低,由海底电缆(OBC)、海底节点(OBN)和海底地震仪(OBS)采集的多分量地震数据越来越多。不同于拖缆采集,海底检波器布设更为灵活,理论上更容易实现高覆盖、长偏移距、宽方位角观测,且能够较完整地记录P波与S波的三维矢量振动信息。这些优势可以在解决气云区与盐下复杂构造成像[1-3]、岩性划分[4-6]、裂缝检测[7-9]以及流体识别[10-12]等难题时发挥重要作用。
国内外至今已采集了大量海底多分量地震数据,相应的处理与解释通常围绕一次反射PP波和PS波进行成像或开展P-S联合反演。然而,由于海底观测环境的特殊性和海底地质条件的复杂性,尤其是自由表面与海底界面的存在,导致海底地震记录波型种类多、波场特征十分复杂。这就需要研究各类波型成分的产生机制,并针对其特征进行压制或利用,才能满足后续全波成像与联合反演的要求[2-3]。
除涌浪噪声之外,Scholte波、导波、鬼波以及各类多次波都会给速度分析与偏移成像带来影响。首先,Scholte波和导波等界面波的传播特征受海底附近介质参数控制[13-14],故可以用于反演海底浅层纵、横波速度结构[15-16],除了帮助海底工程建设或油气井场调查外,还可以为PP和PS波反演成像提供初始速度模型[17-18]。其次,鬼波是由于震源气枪或检波器在特定水深放置所产生的自由表面多次波,通常与一次反射波存在微小时差,会导致显著的陷波效应,严重降低了地震成像分辨率。值得注意的是,由于OBN/OBC在海底采集波场信号,检波端鬼波通常被视为检波端多次波,因此海底多分量数据中的鬼波一般特指源端鬼波。国内外学者相继提出了联合反褶积[19]、格林定理[20]、逆散射级数[21]以及稀疏τ-p反演[22]等方法压制鬼波,获得了更宽频带的地震数据处理结果。
自由表面多次波压制一直是海洋地震数据处理最关键的环节。针对拖缆数据,最常用的方法包括Radon变换滤波法[23-24]、预测滤波法[25]以及波动方程自由表面多次波预测-相减法(SRME)[26-29]等。近年也涌现出许多基于深度学习的多次波压制方法[30-31]。对于海底多分量地震数据,人们常采用基于声波理论的PZ叠加[32-33]或者基于弹性波理论的上-下行P/S波分离对检波器端的表面多次波进行压制[34-35]。受海底地形、洋流以及施工因素的影响,陆检在海底的耦合条件以及检波器的方向旋转都会给基于波场分离的多次波压制造成影响[36]。近年来,随着研究的逐步深入,人们开始利用表面多次波缓解复杂地质体(如盐丘)下部照明不足问题,并能够大幅提高浅层成像分辨率[37-40]。
总之,由于海底界面、自由表面和海水层的存在,以及海底介质条件和观测环境的影响,海底多分量地震数据波型成分非常复杂。文献调研发现,目前对海底多分量地震数据特征和影响因素的研究相对较少,认识不够清晰。因此,本文拟厘清不同水深和海底介质条件下海底多分量波场的成分特征和影响机制,为面向反射PP与PS波成像的数据处理提供指导。一方面,通过不同水深、典型海底介质模型合成多分量地震数据,分析主要波型成分的运动学和动力学特征,揭示相关的影响机制。另一方面,利用东海浅水(约82m)与南海深水(约1200m)实际观测的OBS数据验证上述认识的合理性。最后,结合本文认识,对基于海底多分量数据的全波速度建模与偏移成像提出建议。
1 海底多分量地震数据数值模拟分析
不考虑洋流、海浪、海底地形地貌等外部环境和地下地质构造因素,在海底观测的多分量地震数据主要受水深和海底附近物性特征(如软海底和硬海底)等因素影响。如图1所示,除PP波和PS波等一次反射波之外,OBC/OBN多分量记录中还存在能量较强的鬼波、多次波、面波和导波等,其中多次波又可分为源端多次波与检波点端多次波。这些波型成分在地震记录中相互干扰,给多分量地震数据预处理及后续针对反射P波和S波的速度分析、偏移成像以及联合反演带来诸多困难。本节首先基于典型海底介质情况进行弹性参数建模,利用高精度的谱元法弹性波数值模拟方法合成不同水深条件下包含各类波型成分的海底多分量地震记录,进而分析其波型特征、影响因素及其物理机制。
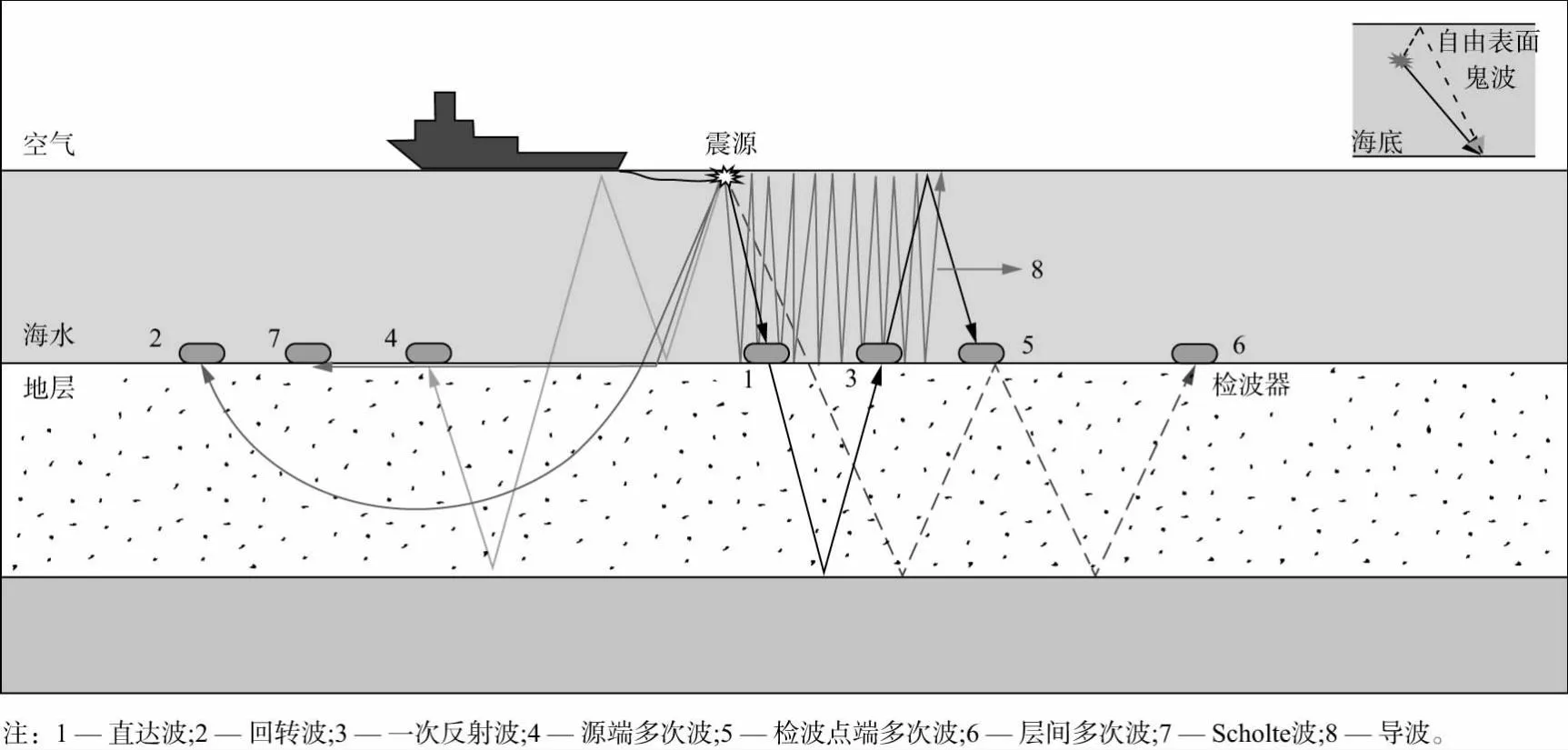
图1 海底多分量地震观测与波型成分示意
1.1 海底介质弹性参数建模
根据海底介质物性差异,可分为硬海底和软海底两种情况,前者通常由于基岩出露引起,后者则往往是因为松软的海洋沉积物。对于比较普遍的海底存在未固结软性沉积物情况,纵-横波速度比值较大,且随深度快速变化[41-42]。此时,海底沉积物主要有砂质沉积和泥质/黏土沉积等类型。表1展示了两种不同海底沉积地层中纵波速度(vP)、横波速度(vS)的经验关系式[43-45],其中z表示相对海底的地层深度。密度(ρ)模型则根据经验公式由纵波速度转换获得[46],这里采用ρ(z)=310vP(z)0.25。

表1 软海底浅层速度统计公式
在软海底情况下,本文主要基于砂质沉积类型构建弹性参数模型。对于常见的海底薄互层沉积,按10m到60m的随机厚度对低速沉积层进行剖分,分别以总厚度为100m和400m两种情况构建典型软海底模型。为了简化分析,暂不考虑沉积层可能存在的粘弹效应。在硬海底情况下,认为海底没有覆盖低速沉积物,故分别以纵横波速度比3.00和1.73构建两种硬海底模型。为便于波场模拟与分析,假设海底软(硬)介质之下由水平层状介质组成,层厚度为50~150m。图2展示了具有400m砂质沉积物和纵横波速度比为1.73的软、硬海底弹性参数模型。结合30,100,300,1000m这4种不同水深,共构建出16种弹性介质模型供波场模拟分析使用。
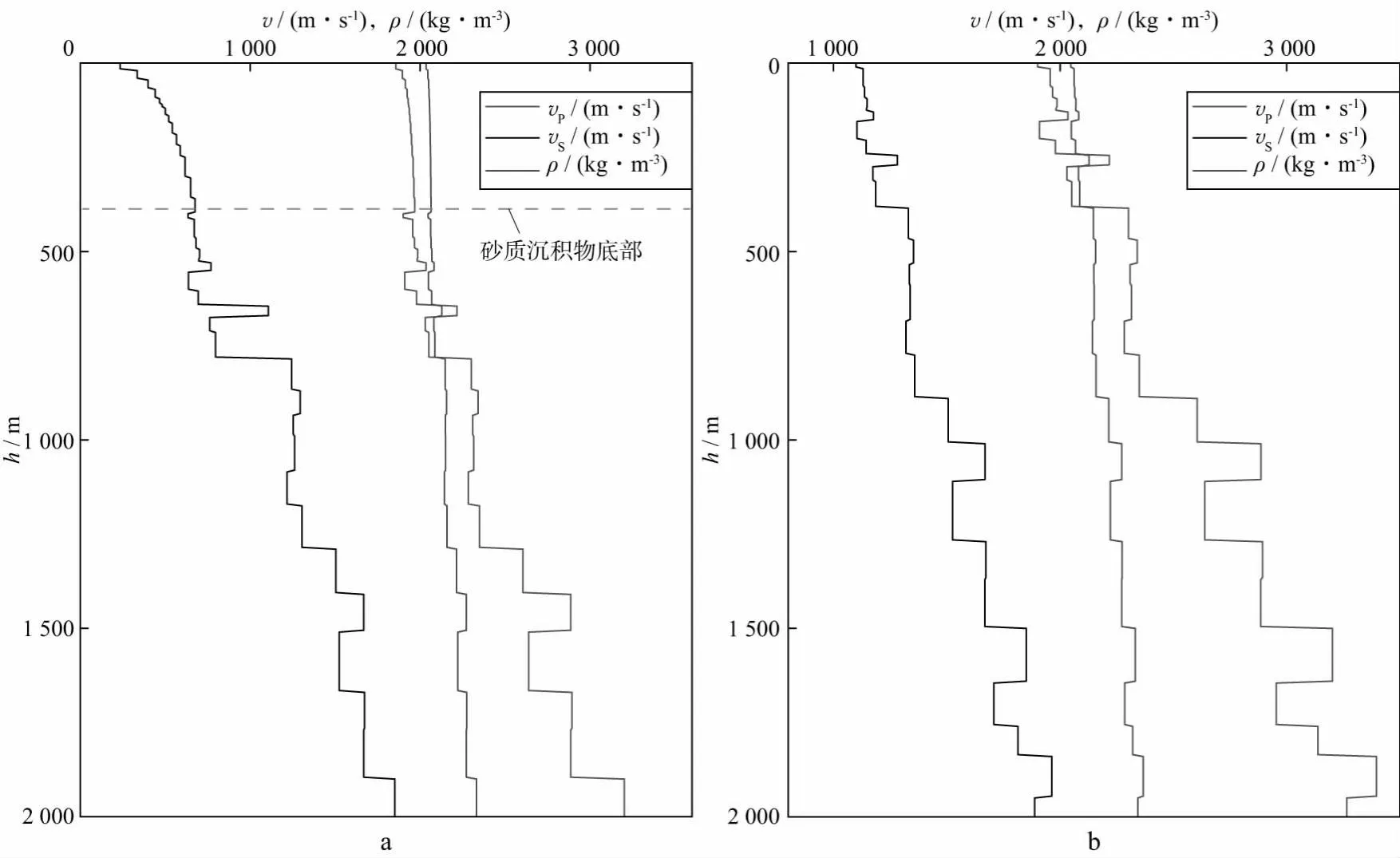
图2 软、硬海底弹性参数模型a 沉积物厚度为400m的软海底模型; b 海底岩石纵横波速度比为1.73的硬海底模型
1.2 海底多分量记录数值模拟与特征分析
由于海底介质波速(尤其是横波速度)非常低,基于常规均匀网格的有限差分算法受数值频散影响很大,而谱元法[47]结合了伪谱法的精度优势和有限元方法网格剖分的灵活性,更适合含固液界面的海底多分量地震波数值模拟。因此,本文利用开源SPEFEM2D软件[48],针对上文典型介质模型进行数值模拟,对合成的海底多分量地震记录进行分析,揭示各种波型成分的产生机制及其影响因素。
1.2.1 数值模拟与分析
仿照OBC/OBN多分量地震采集方式,将震源设置在海面以下5m,采用主频为20Hz的Ricker子波作为震源时间函数,以10m的炮间隔和8.0km的最大炮检距在水平海底记录时长为5s的声压-质点振动速度波场信号。实验发现,对于同一类性质的海底模型,水深变化导致的合成数据特征变化最为显著,而沉积层厚度变化或纵横波速度比变化引起的数据特征变化则相对较弱。因此,为了节省篇幅,这里针对100m和1000m水深情况,展示沉积物厚度为400m的软海底模型和海底介质纵横波速度比为1.73的硬海底模型对应的二维三分量(2D3C)数据,即质点速度水平(X)分量、质点速度垂直(Z)分量和声压(P)分量的共检波点道集。如图3和图4所示,不同水深条件对多分量波场数据影响十分明显。在浅水情况下,不论是软海底还是硬海底,在全频带的合成地震记录中难以观察到Scholte波,只有在0~4Hz的低频分量中才能观察到,并且此频段内Z分量上Scholte波能量要强于其它分量。浅水区导波能量很强,在软海底情况下其大部分能量位于折射波与直达波下方,其传播速度略低于直达波;而在硬海底条件下,严重的频散效应[49]致使导波震相连续性变差。另外,浅水情况下多次波与一次波时差不大,极易产生混叠,给浅水多次波去除带来了很大的挑战。但是在深水合成地震记录中,Scholte波和导波则基本消失[50]。同时,多次波与一次波运动学差异明显,相对容易识别。我们注意到,在软海底情况下X分量和P分量的中小偏移距以纵波成分为主,而Z分量的中小偏移距由转换横波能量主导,但受多次(纵)波影响较为明显(在图中标识为M1);随着阶次变高,多次波入射角变小,在X分量观察到的多次波越来越少。如图4,在硬海底情况下,X分量和Z分量中小偏移距同时存在较强纵波与转换横波能量,模式耦合现象严重(见图4中P&S指示区域)。相对而言,硬海底所产生的Scholte波视速度更大,能量更强(图4a)。此外,在上述合成数据中也存在源端鬼波,可以从P分量近偏移距直达波上观察到。

图4 硬海底模型2D3C共检波点道集(右上角子图为虚线框内的数据经过0~4Hz带通滤波的结果)a 水深为100m; b 水深为1000m
1.2.2 海底界面影响
地震波场在海底固-液界面处会发生复杂的模式转换,不同性质的界面(如软、硬海底)会影响纵、横波的能量分配关系和多分量记录的特征。理解其中的物理机制对多分量数据处理,尤其是全波成像与反演非常关键。本节将基于前文构建的软、硬海底模型,依据Zoeppritz方程计算海底界面反射、透射系数,并分析对海底多分量地震数据记录的影响。注意,海底界面下方薄互层产生的调谐效应也会对海底反射系数产生影响,这里暂不予考虑。
通常认为,水检与陆检分别在紧挨海底界面上方(海水中)和下方(沉积地层中)接收信号。根据入射波场的类型,界面处的模式转换效应可以分为下行P波(P+)、上行P波(P-)以及上行S波(S-)3种入射情况。如图5b所示,以二维为例,到达海底的下行P波通常为直达波或自由表面多次波,在海底界面入射时会产生反射、透射及模式转换。因此,在界面上方的水检将接收到入射波与反射P波(P-);而在界面下方的陆检则接收到透射波和转换波。另外,来自海底以下地层反射产生的P-或S-入射到海底界面时(图5c和图5d),水检只会接收到上行透射(蓝线箭头),而陆检则会同时接收到上行入射P-或S-波(黑线箭头),以及经海底反射的短程下行P+波(深蓝线箭头)和短程下行S+波(红线箭头)。这些波型在水平和垂直方向上的投影干涉叠加,即形成最终的海底2D3C记录。
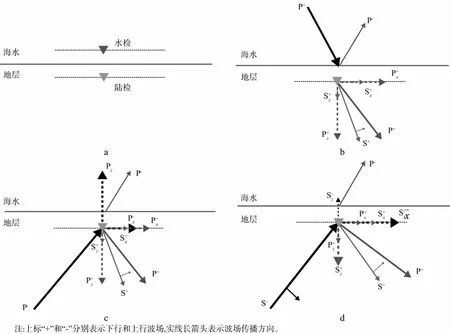
图5 海底界面波场能量分配关系a 水检和陆检在海底的相对位置; b 下行P波入射情况; c 上行P波入射情况; d 上行S波入射情况
多分量记录中不同波型的具体特征与海底界面性质关系密切。海底介质弹性参数的差异会引起弹性波场反射、透射及转换系数的变化,从而影响不同波型成分在界面处的能量分配关系。由于海水的粘滞系数几乎为0,可以认为波场在海底界面处的垂向位移与垂向应力均连续,由此可以导出平面波入射情况下P或S波的各类反射/透射系数[51-52](见附录A)。一方面,根据前文构建的软海底模型参数计算反射、透射系数随入射角变化的曲线,发现当P+和P-入射时(图6a和图6b)P波反射系数很小,透射系数近似为1,同时P-S转换系数很小,表明软海底界面对P波能量的改造作用很小,主要以透射为主,少部分能量被反射或转换为S波。而当S-上行入射时(图6c),水层与海底界面S波下行反射系数几乎为1且S-P转换非常微弱。分析图5d可知,此时陆检位置处S-与S+能量一致,其垂向投影将相互抵消,导致陆检垂直分量中几乎不包含S波成分,这与前文合成数据的特征也非常吻合(见图3a和图3b)。另一方面,针对前文硬海底界面模型,反射/透射系数随入射角的变化关系如图7所示。当P+或P-入射时,透射系数变小,在海底界面处产生更强的反射及P-S模式转换。而当上行S-入射时,也会发生很强的S-P模式转换,且S波下行反射系数随入射角增大逐渐变小,此时陆检垂直分量中S-与S+成分很难抵消,会导致更多的S波能量出现在垂直分量记录中。综上分析可知,随着海底介质由软变硬,界面上的反射系数增大,海底界面效应会导致多分量记录的中小偏移距P波与S波耦合更为明显,在偏移成像与弹性参数反演中需要更谨慎地进行P/S分离处理。
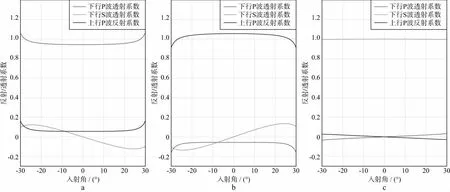
图6 软海底界面反射/透射系数随入射角变化关系a 下行P波入射; b 上行P波入射; c 上行S波入射
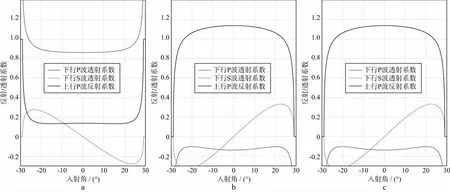
图7 硬海底界面反射/透射系数随入射角变化关系a 下行P波入射; b 上行P波入射; c 上行S波入射
1.2.3 自由表面效应
由于海水与空气之间自由表面的存在,海底多分量地震数据中存在多种与表面效应相关的波型成分,包括源端鬼波、源端多次波以及检波点端多次波等。其中某些频率成分的延迟时间恰巧与一次反射波相应谐波成分的周期成整数倍关系,因而会与一次波发生相消干涉,导致数据频带上出现陷波现象(公式推导见附录B)。近偏移距陷波点的理论计算公式可以近似表示为:
f=nc/(2z)
(1)
其中,n=0,1,2,…表示陷波点序号,c表示海水波速。当z表示震源深度时,(1)式表示源端鬼波(图8绿线)引起的陷波频率值;当z表示检波点深度时,(1)式表示检波点端多次波(图8红线)引起的陷波频率值;当z表示震源到海底的距离时,(1)式表示源端多次波(图8蓝线)引起的陷波频率值。由于海底多分量观测中检波器深度通常远大于震源深度,根据(1)式可知海底多分量地震数据中源端多次波引起的陷波效应要弱于检波点端多次波。此外,鬼波和多次波共同导致零频率附近能量衰减,因此需要通过消除鬼波和多次波来恢复数据低频成分。
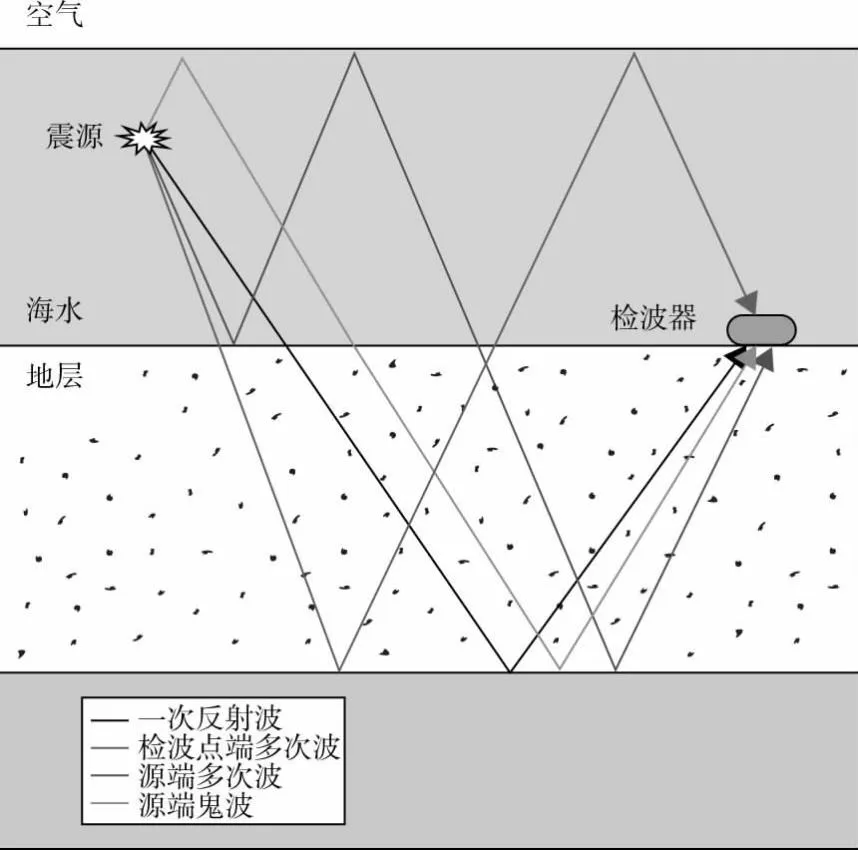
图8 海底多分量记录中的自由表面效应示意
为了直观了解自由表面对海底观测地震信号的影响,下面针对浅水与深水软海底模型,分别对比自由表面和最佳匹配层(PML)边界条件下合成数据的频谱差异。图9a展示了100m水深软海底模型Z分量的频率-波数谱,可以看到明显的陷波效应。由于震源深度为5m,源端鬼波在直流分量(0Hz)附近的陷波导致低频能量减弱,而第2个陷波点则位于150Hz附近;当对海表面施加吸收边界时,则观察不到陷波问题(图9b),低频能量也更强。图9c中的黑色箭头代表理论计算的陷波位置,与频谱中的陷波点十分吻合,由此可以判断,在自由表面条件下,海底多分量数据中有效频带范围内的陷波效应主要由多次波产生。当水深增加到1000m时,在有效频带范围内陷波点个数大幅增加,从频率-波数谱中能观察到明显的陷波效应(图10a)。但此时由于检波端一阶多次波与一次反射波时差增大,几何扩散效应导致两者振幅差异变大,陷波幅度有所降低(图10c)。此外,高阶多次波同样会引起陷波效应,但由于它与一次波的路径差异更大,引起的陷波属于次级效应,本文不再讨论。

图9 浅水软海底模型Z分量频率-波数谱a 自由表面;b 海表PML边界;c 零波数处的振幅谱对比
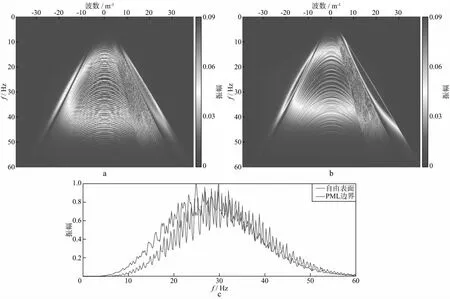
图10 深水软海底模型Z分量频率-波数谱a 自由表面; b 海表PML边界; c 零波数处的振幅谱对比
2 实测海底多分量地震数据特征分析
为了证实前面对海底多分量地震记录的波型成分、特征、影响因素及其物理机制的认识,分别对东海浅水区与南海深水区OBS地震数据进行分析。
2.1 东海浅水OBS数据
东海浅水OBS数据,由中海油、同济大学与中石化三方合作,于2017年依托三维地震勘探项目采集于平均水深82m的东海YQ探区。在采集过程中,将100台国产OBS仪器通过绳系的方式,以100m的间隔抛投于海底并接收数据。记录长度为6s,采样间隔为0.5ms。气枪震源信号的频带范围为5~88Hz,震源激发间距为6.25m。预处理包括时钟校正、重定位、旋转校正、时间重采样、3D到2D校正、带通滤波和插值等。图11显示了预处理后第45号OBS对应的声压分量、陆检速度水平和垂直分量共接收点道集,从中可观察到能量很强的导波,X分量主要为S波成分,Z分量和P分量主要为P波成分。在4Hz以下低频范围内可看到X分量和Z分量中存在明显的Scholte波。为此,WANG等[16]利用Scholte波信号频散分析反演出该测线海底浅层的横波速度结构。但是,由于所采用的声压检波器无法记录5Hz以下低频成分,因此声压记录中没有明显的Scholte波信号。此外,由于水深较浅,自由表面相关的多次波非常发育,并且与一次波很难区分。从P分量的频率-波数谱(图12)中可以看到,零波数成分对应的频率值大约为9,18,27Hz等,与理论陷波点位置基本吻合。上述波型特征与前文浅水软海底合成多分量记录特征一致,也与同一套数据海底介质参数反演结果相吻合[36]。
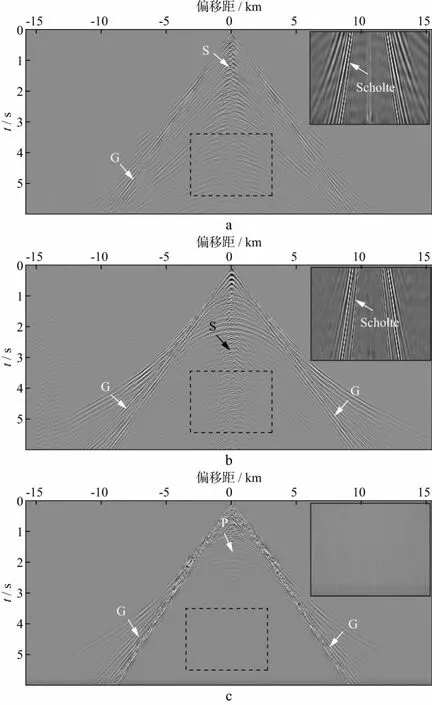
图11 东海浅水OBS数据2D3C共接收点道集(右上角为0~4Hz带通滤波后虚线框内局部放大显示)a X分量; b Z分量; c P分量

图12 东海浅水OBS数据声压分量频率-波数谱(白色箭头指示陷波效应)
值得注意的是,海底起伏或障碍物导致的仪器倾斜或检波器共振等因素会使得Z分量中存在明显的S波泄漏[53-54],这一现象在东海绳系OBS数据中尤为明显(如图11b黑色箭头所示)。此外,在X分量中观察到的PS波震相个数要多于Z分量或P分量中的PP波震相个数。刘学义等[55]也发现,即便经海底上-下行P/S波分离之后,在上行S波数据仍然可以发现类似现象,他们认为这与源端水层鸣震有关,并且探讨了在波动方程转换波走时反演中克服其影响的方法。
2.2 南海深水OBS数据
南海某工区海底多分量数据的平均水深大约为1200m。该二维测线长度约为16km,由抛载式OBS采集到685炮气枪震源激发的波场信号,震源间距为25m,记录长度为8s,采样间隔为1ms。图13 展示了经过水平分量方向旋转、涌浪与随机噪声去除以及带通滤波等预处理后的典型共接收点道集,可以看到如下特征:①在低频成分中依然见不到明显的Scholte波;②由于海水层非常厚,波场在海底与海面之间的振荡变弱,直达波附近未见明显的导波;③自由表面产生的多次波能量很强,在三分量记录上均可以清楚地看到一阶和二阶多次P波。在P分量上,主要能量为P波,几乎观察不到S波。而在X分量中虽然可以看到少量多次P波的能量泄露(图13a黑色实线箭头所示),但总体上以S波为主,且转换PS波震相数量明显多于P分量,其中绝大部分应与源端水层鸣震有关,这一特点与东海浅水OBS数据类似。如图14箭头所示,声压分量的频率-波数谱中可以观察到明显的陷波现象;由于深水环境,多次波与一次波振幅差异较大,虽然陷波点个数远比浅水数据多,但是陷波幅度明显减弱。上述波型特征与前文深水环境合成多分量记录特征基本一致。由于气枪所产生的气泡震荡所带来的震源噪声,3个分量浅层小偏移距以及某些远偏移距都存在明显的“气泡”效应(图13虚线箭头所示)。此外,对比这两个工区OBS数据还发现深水条件下随机噪声减弱,相对于浅水条件信噪比有明显提升。

图13 南海深水OBS 2D3C共接收点道集a X分量;b Z分量;c P分量

图14 南海深水OBS声压分量频率-波数谱
3 讨论
认识不同水深、典型海底介质情况下OBC/OBN数据的波型成分与分布特征,有助于针对性地研究和应用信号处理、速度建模以及偏移成像的方法策略。
首先,浅水环境下导波与Scholte波较为发育,利用其频散特征反演海底介质弹性参数[18,56],可以为分离上-下行P/S波、深度域偏移成像提供比较可靠的海底浅表层速度模型。在深水环境下,导波与Scholte波可以忽略,而表面多次波的影响也明显减弱,直接针对多分量数据的弹性波成像与反演容易获得好的效果。
其次,海底岩石物性影响固-液界面上的能量分配关系,是决定多分量数据P/S模式转换与耦合程度的关键因素。在进行上-下行P/S波分离与P/S波模式解耦时,需要考虑工区内海底软硬特征采用合适的方法或流程[36]。在此基础上,可以分阶段进行声波、弹性波走时或全波形反演,基于恰当的多尺度策略构建宽谱的纵、横波速度模型,从而满足高分辨率矢量全波成像的要求[57-60]。
此外,表面多次波的干扰极大地挑战传统偏移成像和速度分析方法所基于的一阶散射理论假设,目前压制或利用多次波的方法主要针对海面拖缆数据[38-39],需要深入地研究适合OBC/OBN数据的多次波速度建模与偏移成像方法[55],最大限度地释放多分量数据的潜力。
4 结论
自由表面、海底界面的存在以及水层的影响,导致海底多分量地震数据的波型成分非常复杂,而且随水深、海底环境和介质条件变化而改变。浅水多分量数据中,导波、Scholte波等噪声较强,且自由表面多次波与一次波难以区分,导致OBC/OBN数据处理面临更大的挑战。海底界面透射/反射系数分析表明,在软海底条件下,弹性波模式转换相对较弱,P-S波耦合不严重,近偏移距Z分量可视为P波,X分量以S波为主。但在硬海底条件下,P-S波之间的模式转换增强,中小偏移距也存在较强的模式耦合,需要谨慎地进行上-下行P/S波分离以满足后续速度分析与偏移成像的要求。
附录A 海底界面反射/透射系数公式
依据文献[44],当下行P波入射到海底界面时(图5b),反射/透射系数满足:
(A1)
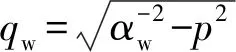
当上行P波入射到海底界面时(图5c),反射/透射系数满足:
(A2)
当上行S波入射到海底界面时(图5d),反射/透射系数满足:
(A3)
附录B海底多分量地震数据频带陷波公式推导
首先,如图B1所示,以检波点端一阶多次波为例,基于P波传播路径分析多次波对海底多分量地震数据频带的影响。设震源深度为d,海水深度为z,地下界面深度为h,炮检距为D。为简便起见,图中忽略波场因透射产生的传播角度变化。将水速设为c时,那么一次反射波与检波点端一阶多次波的到达时差Δt可以表示为:
(B1)
在小角度反射时检波点端多次波延迟时间大致等于P波在水层中的双程旅行时。设海面反射系数为R0,海底界面处下行波场透射系数为T1,上行波场透射系数为T′1,反射系数为R1,地下界面反射系数为R,那么,陆检接收到的地震信号x(t)可近似表示为:
x(t)=T1Rs(t)+T1RT′1R0T1s(t-Δt)
(B2)
其中,s(t)表示震源信号,等号右边第一项为一次反射波信号,第二项为检波点端一阶多次波信号。对(B2)式做傅里叶变换:
X(f)=T1Rs(f)G(f)
(B3)
其中,f表示频率,G(f)=(1+T′1R0T1e-i2πfΔt)。进一步地,因为R0=-1,将接收信号的振幅谱A(f)表示为:
(B4)
由公式(B4)可知,在某些频率处A(f)陷入局部极小,即发生多次波与一次波相互抵消的现象,称之为陷波点,其频率满足:
(B5)
其中,n=0,1,2,3,…。注意,由公式(B4)可知,海底多分量数据与常规拖缆也有差异,受海底界面处透射与反射系数共同影响,多次波与一次波无法完全抵消,即陷波问题比海面拖缆数据相对弱一些。
一次反射波与源端一阶多次波到达时差同样可以用公式(B1)计算获得。此时,接收信号可近似表示为:
xs(t)=T1Rs(t)+R1R0RT1s(t-Δt)
(B6)
参考前文推导,接收信号振幅谱As(f)可以表示为:
(B7)