考虑数据分布偏移的短期居民净负荷预测方法

王瑞临, 赵健, 孙智卿, 宣羿

(1.上海电力大学电气工程学院, 上海市 200090;2. 国网浙江省电力有限公司杭州供电公司,杭州市 310007)

0 引 言

随着分布式可再生能源发电的不断发展,净负荷,即用户总负荷需求与新能源出力之差,日益成为电力系统关注的问题。准确的居民净负荷预测可以保证电力系统的可靠性,更重要的是可以促进电力系统对可再生能源发电的适应[1]。新能源发电的高随机性为净负荷注入了更多的不确定性,进而使得净负荷数据分布偏移更为频繁和严重。数据分布偏移是指数据的概率分布发生变化,其会导致模型在历史数据中学习到的特征信息不再完全适用于未来数据,从而降低了数据的可预测性。在需求侧,如气温上升[2]和电价上涨等[3]导致负荷需求数据分布发生变化。在供应侧,辐照水平、风速等变化会影响可再生能源发电量的数据分布。由于净负荷的不确定性由负荷需求的不确定性和新能源发电的不确定性组成,这些不确定性因素的综合影响将使净负荷数据分布的变化更加复杂和频繁。

现有居民净负荷预测研究可分为间接预测和直接预测。间接预测通过将净负荷数据分解为负荷需求部分和可再生能源发电部分来降低净负荷的巨大波动性。文献[4]提出了一种滚动调节优化的VMD-SaE-ELM(variational mode decomposition-selfadaptive evolutionary-extreme learning machine)净负荷超短期预测方法,减小了常规机组的调峰压力。文献[5]将数据分解后的误差通过不同的影响权重与净负荷误差相联系。文献[6]通过相关性分析和网格搜索方法将净负荷分解为光伏发电量、实际负荷和残差。然而,间接预测依赖于分解方法和预测方法的准确性,这会导致误差累积。

直接预测是直接使用净负荷数据进行预测,文献[1]提出了一种概率不确定性模型,通过贝叶斯深度学习模型同时捕获净负荷的随机不确定性和模型不确定性。文献[7]提出了一种全参数化序列深度学习模型,来学习净负荷中的最优特征和整个概率分布。文献[8]提出了一种基于特征加权改进的Stacking集成学习净负荷预测方法。文献[9]提出了基于自注意力编码器和深度神经网络的净负荷预测模型,同时集成了负荷、风光、净负荷等多个不确定量。

直接预测依赖高精度的深度学习技术,而深度学习技术默认数据满足独立同分布,其基于经验风险最小化(experience risk minimization, ERM)的学习模式允许模型"不计后果"地学习数据中的特征信息。当数据分布不断变化时,现有模型在历史数据中学习到的特征信息不再适用于未来数据,从而使得净负荷预测精度难以得到保证。

因此,本文提出了一种基于不变风险最小化(invariant risk minimization-uncertainty, IRM)的短期居民净负荷预测方法,以提升净负荷预测的精度。面对数据分布的变化,IRM考虑同时学习最小误差和不同分布下的不变性[10],并通过学习不同数据分布下的不变特征来实现对不可见环境的鲁棒性。首先,对净负荷中的数据分布偏移问题进行了探索。其次,建立了基于不变风险最小化-不确定性加权-长短期记忆神经网络(invariant risk minimization-uncertainty weighting-long short-term memory neural network,IRM-UW-LSTM)的净负荷预测模型。其中,通过IRM建立了一个双目标问题,包括准确预测和学习跨不同数据分布的不变特征;通过长短期记忆神经网络(long short-term memory neural network,LSTM)处理时间序列数据的非线性特征;通过基于不确定性加权(uncertainty weighting,UW)的目标平衡机制避免过度实现任一目标;此外,通过引入分位数回归方法将本文方法扩展到概率预测。最后,通过基于澳大利亚Ausgrid公司提供的真实居民电表数据从确定性预测结果、概率预测结果、不同数据分布偏移程度和不同光伏渗透率等多个维度验证了所提方法的有效性。

1 净负荷数据分布偏移探索

本文利用几种常用数据分布比较方法验证了净负荷预测(net load forecasting,NLF)中的数据分布偏移程度高于用电量预测(electricity consumption forecasting,ECF)。用于比较的数据是澳大利亚Ausgrid公司提供的悉尼地区从2010年7月到2013年6月数百户包含居民净负荷和居民总用电量的数据[11]。

为了避免季节对数据分布比较的影响,选择了四个季节中每个典型月份的数据(南半球春、夏、秋、冬分别使用10月、1月、4月和7月的数据),分别比较不同年份同一季节的数据分布偏移程度,如图1所示。此外,为反映不同月份下的数据分布偏移情况,还将重点关注同一季节下相邻月份的数据分布偏移程度,如图2所示。

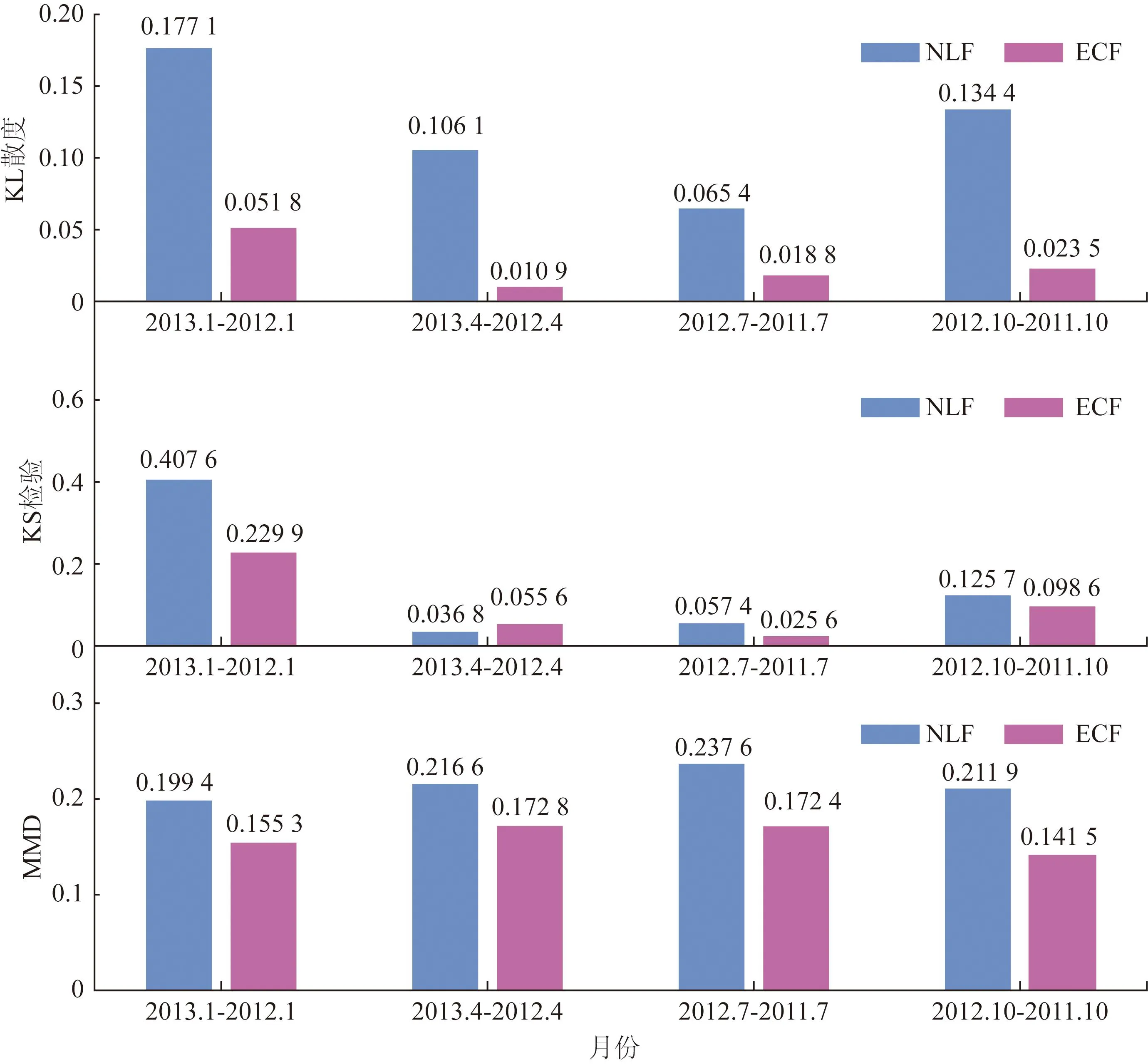
图1 不同年份同一季节数据分布偏移比较Fig.1 The compare of the degree of the data distribution shift under the same season for different years

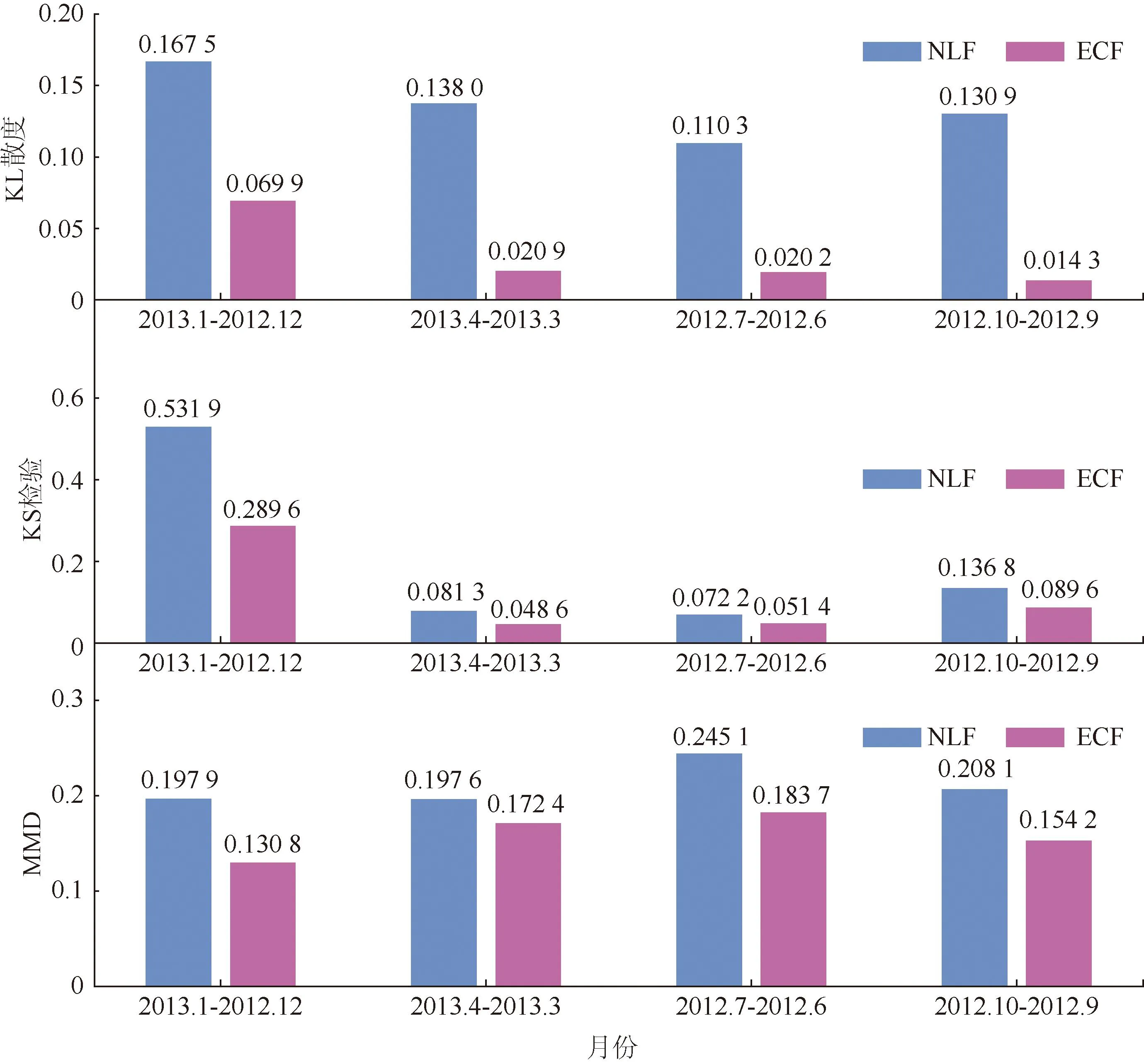
图2 同一季节相邻月份数据分布偏移比较Fig.2 The compare of the degree of data distribution shift adjacent months under the same season

本文采用Kolmogorov-Smirnov(KS)检验[12]、Kullback-Leible(KL)散度[13]和最大平均差异法(maximum mean difference,MMD)[14]进行数据分布偏移评估。从图1可以看出,在不同年份的四个季节中,NLF的KL值和MMD值均明显大于ECF。在KS值方面,除4月份ECF值与NLF值相差不大之外,其余年份NLF值均大于ECF值。这可能是由于KS检验对数据分布的中间部分更敏感,而对两端不够敏感。值得注意的是,由于冬季昼短夜长,光伏发电量最少,因此南半球7月份的数据分布偏移较小。从图2中可以看出,在所有相邻月份的数据分布偏移比较中,NLF的数据分布偏移程度大于ECF。另一个有趣的发现是,KL散度对数据分布偏移最为敏感,而MMD由于比较的是多维数据分布,敏感度较低。

通过三种统计方法,可以发现净负荷的数据分布偏移程度大于传统用电量数据。这表明居民净负荷数据面临更严重的数据分布偏移问题,历史数据与未来数据的相关性将降低。此时,原有模型训练集与测试集数据独立同分布的前提也将被削弱,从而影响现有模型对净负荷预测的有效性。因此,解决净负荷预测中的数据分布偏移问题具有现实意义和挑战性。

2 基于IRM的净负荷预测理论和建模

2.1 IRM与数据分布偏移的关系

基于深度学习的方法在计算机视觉、语音识别和文本识别等许多应用领域取得了巨大成功[15]。然而,大多数方法依赖于使用ERM进行优化,当测试数据的分布与训练数据的分布发生变化时,基于ERM的模型的性能会下降。IRM能够通过学习数据跨分布的不变性来克服数据分布偏移,对未来数据具有鲁棒性。需要关注以下两个问题:1)IRM如何克服数据分布偏移;2)IRM学习的净负荷数据中的不变特征信息是什么。

对于问题1),ERM合并来自所有训练环境的数据,并利用训练数据中的所有特征训练一个模型,以最小化数据的训练误差。而在最小化训练误差的过程中,基于ERM的模型会导致模型不计后果地吸收训练数据中发现的所有相关性[10]。此时,面对未来分布变化的数据,模型的预测精度会下降。对于IRM,以本文的净负荷预测为例,首先将所有的净负荷训练数据进行合理的划分,形成多个训练环境。这些训练环境下的净负荷数据分布本身是不同的。面对未来的数据,IRM保持了部分ERM的性能,即对同一分布下的数据寻求最小训练误差;同时,对不同分布下的数据可以学习跨不同数据分布的不变性。

对于问题2),在数学上,本文的目的是找到式(1)所示的变化环境e中的不变信息E[Ye|(Φ(Xe)=y]:

E[Ye1|(Φ(Xe1)=y)]=
E[Ye2|(Φ(Xe2)=y)]=···=
E[YeN|(Φ(XeN)=y)]

(1)

式中:E为条件期望值;Φ:X→y为一个数据表示;e为环境;N为环境总数量;y为数据表示Φ下因变量的数值。图3列举了影响净负荷数据分布的几个主要因素。环境因素(温度、辐照度)主要通过影响光伏出力来影响净负荷,而经济因素和社会因素主要通过影响居民用电需求来影响净负荷。所有箭头表示两个因素之间的函数关系。图3(a)、(b)、(c)和(d)分别表示4个时间段各因素对净负荷的影响关系。红色部分代表发生变化的影响因素。图3(a)显示了第1个时间段的所有影响关系。图3(b)表示第2个时间段与第1个时段相比辐照度发生了变化,进而导致了净负荷的数据分布发生偏移。图3(c)中表示了温度的变化,同时红色箭头表示经济因素与用户行为之间非线性关系的变化(例如,用户的整体经济水平没有变化,但售电政策发生了变化)。图3(a)、(b)、(c)中颜色不变的部分即为3个时间段内的不变特征信息。学习不变特征信息可以充分利用净负荷历史信息,更好地应对图3(d)中第4年未知的净负荷数据分布变化。

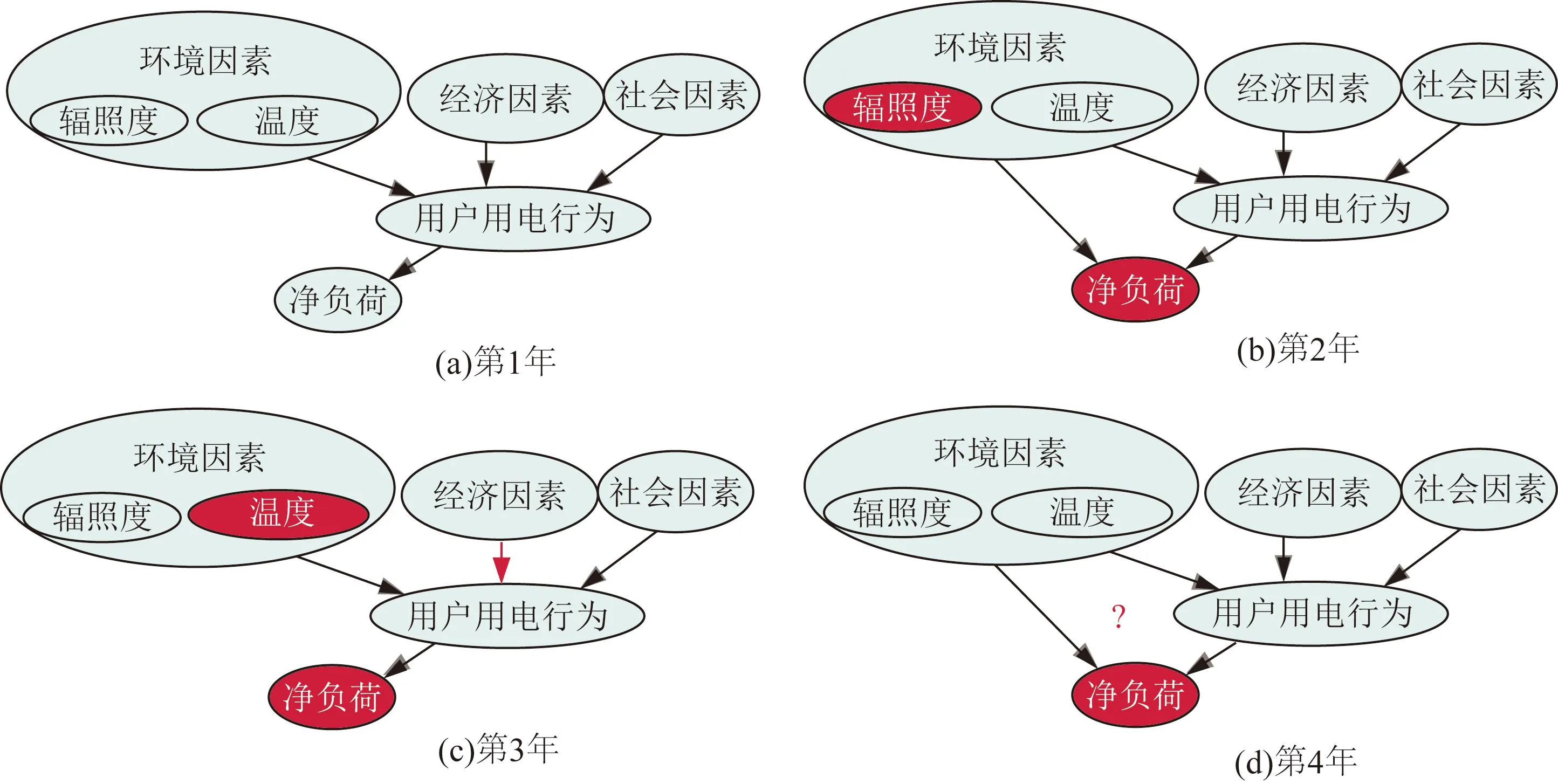
图3 净负荷预测中的不变特征信息示例Fig.3 Invariant feature information in the net load forecasting

2.2 IRM-LSTM模型建立

LSTM神经网络是基于时间序列的模型,可以在历史信息和未来信息之间建立时间关联性。此外,LSTM网络还可以克服循环神经网络(recurrent neural network, RNN)中的梯度消失和梯度爆炸问题。首先描述LSTM网络的结构,如图4所示。

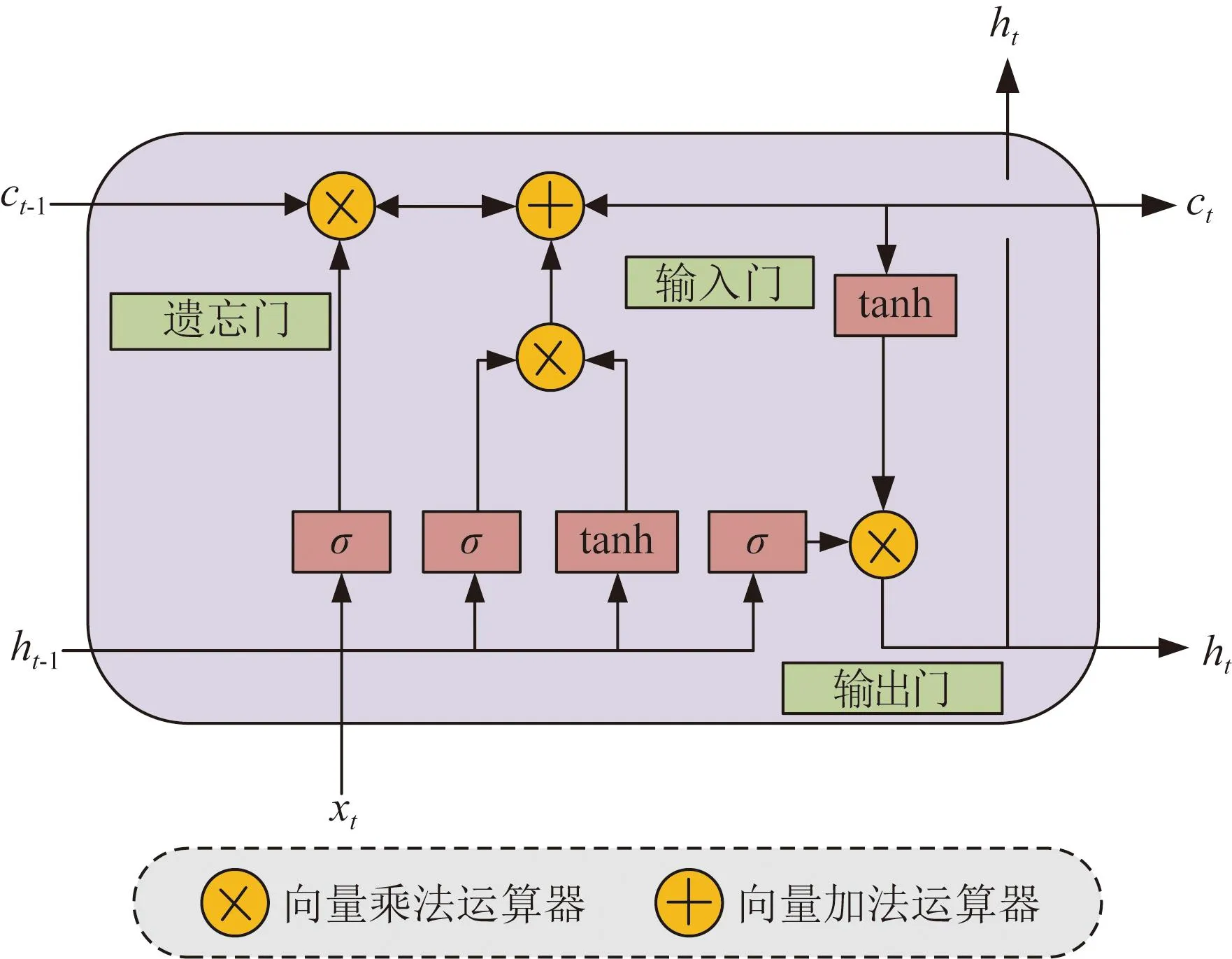
图4 LSTM结构Fig.4 A unit of LSTM

如图4所示,LSTM在某一特定时间步长t的输入是前一状态ht-1和当前输入xt。三个门(输入门、遗忘门和输出门)通过4个全连接的神经元Ft、It、Ot和Gt来实现记忆信息或遗忘功能。具体来说,遗忘门决定有多少t之前的信息可以向前传递,输入门控制新的输入信息,输出门决定在这一时间步输出的信息。对于输出,ht是作为下一时间步输入的短期状态,而ct决定长期依赖性。具体计算公式如式(2)-(5)所示。

Ft=σ(Wfx·xt+Wfh·ht-1+bf)

(2)

It=σ(Wix·xt+Wih·ht-1+bi)

(3)

Ot=σ(Wox·xt+Woh·ht-1+bo)

(4)

Gt=tanh(Wgx·xt+Wgh·ht-1+bg)

(5)

式中:Ft、It、Ot、Gt为全连接神经元;xt为输入向量;ht-1为前一个短期状态;Wfx、Wix、Wox和Wgx分别为矢量xt的权重;Wfh、Wih、Woh和Wgh分别为ht-1的权重;bf、bi、bo和bg为偏置。根据式(6)-(7)计算下一个时间步的输入值ct和ht。

ct=Ft·ct-1+It·Gt

(6)

ht=Ot·tanh(ct)

(7)

根据上述LSTM的结构,LSTM通过将重要的输入信息存储在长期状态中来处理时间序列问题,并根据需要长期保存,在需要时进行使用。

为了克服净负荷预测中数据分布偏移对模型的影响,引入了IRM。IRM从多个不同数据分布的训练环境中学习不变特征预测因子。由于环境的概念对框架至关重要,引入了文献[16]中提出的训练环境的概念:在所有训练环境e∈εtr中,有不同的实验条件,并且在每个环境中都有一个独立同分布的样本(Xe,Ye)。Xe是在环境e下的预测变量;Ye是目标变量。本文中e= [e1,e2,…,eN]为训练环境,N为训练环境数目,etest为测试环境。本文对风险定义为:

R(f)=mine∈εtrRe(f)

(8)

任一环境e的风险定义为:

Re(f)=E(Xe,Ye){L[f(Xe),Ye]}

(9)

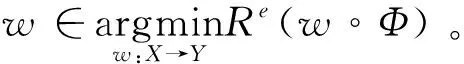
数据表示Φ有两个目标:

1)该数据表示能在相同训练环境下保持准确的预测。

2)在所有e∈εtr中学习一个跨环境预测器,以学习不同数据分布下的不变特征信息。

在数学上,这两个目标被表述为约束优化问题,如式(10):

(10)

式中:w代表分类器;Y、Z表示函数映射的输入或输出;其余符号同上文的定义。

式(10)是一个具有挑战性的双层优化问题,包含优化项Φ和w。根据文献[10]中的详细介绍,得到近似可解的式(11):

(11)

式中:λ∈[0,∞)为保持同分布下精确预测和不同分布下不变预测之间的正则化平衡。在居民净负荷预测问题中,设模型的输入训练集的输入数据和输出标签为:

Xtrain=[x1,x2,…,xn]T∈Rn×dx

(12)

Ytrain=[y1,y2,…,yn]T∈Rn×dy

(13)

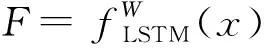
(14)

式中:LIRM是为实现IRM的优化目标而简化得到的损失函数。第一项是LSTM网络中的ERM项,对应目标1),第二项是不变预测项,对应目标2)。

3 基于IRM-UW-LSTM模型的净负荷预测方法

基于上述IRM理论与模型,本节将对所提出的住宅净负荷预测方法的其余部分进行描述。具体来说,包括3个主要过程:1)数据输入;2)目标平衡;3)扩展到概率预测。

3.1 数据输入:特征和环境建立

1)特征建立。

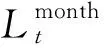
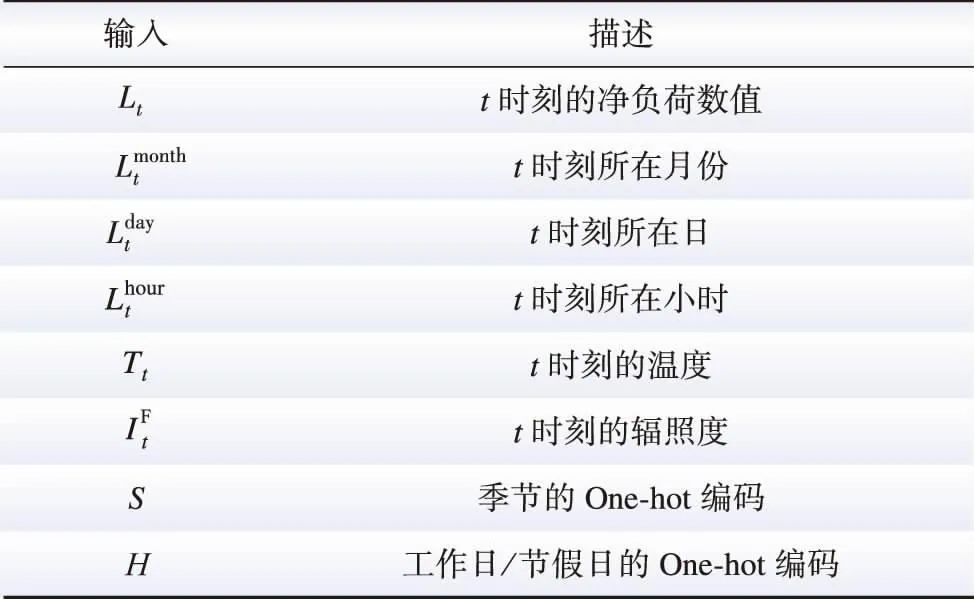
表1 特征建立Table 1 Feature establishment

2)环境建立。

本文提出的方法旨在学习净负荷数据不同分布下的不变特征信息。为了使学习到的不变特征信息有意义,需要尽可能学习具有一致性的数据。尽管可以通过精确的实验设计为Xe创建环境e∈εtr(例如,通过随机化Xe的某些元素),但对于净负荷数据,其环境应尽可能使用原始历史数据创建,而不宜采用人工干预的方式创建环境,以使预测中历史数据与未来数据的相关性尽量不被削弱。同时,对于净负荷预测,很难快速获得数据分布开始偏移的具体时刻,这也是今后工作的主要方向。

RNN的输入原则在于未来数据的输入要在历史数据之后。本文采用了基于并行输入数据集的环境构建方法。以月份作为环境单位为例,首先仅针对第1年的数据(first year data,FYD)使用ERM训练网络,然后针对第2年的数据(second year data,SYD)使用{(1月FYD,1月SYD),(2月FYD,2月SYD),…,12月FYD, 12月SYD)}作为IRM训练的两个环境输入网络。此外,对于第3年的数据(third year data,TYD),使用{(1月FYD,1月SYD,1月TYD),(2月FYD,2月SYD,2月TYD),…,(12月FYD,12月SYD,12月TYD)}作为IRM训练的三个环境输入网络。

3.2 目标平衡机制:不确定性加权

通常需要花费大量精力选择合适的模型参数,如IRM中的平衡项λ∈[0,∞),即预测能力和不变性预测因子之间的目标平衡。否则,方程式(11)可能无法执行式(10)中的约束条件,导致性能不理想。对于式(14)中的λ∈[0,∞),可以采用多任务学习的方法对式(15)进行调整,以更好地分配目标1)和目标2)的学习权重。在多任务损失函数式(15)中,计算每个任务的权重是一项计算量极大的工作。如果模型将这些权重作为参数之一进行学习,将大大减少计算量。

L=LERM+λLIRM

(15)

式中:LERM、LIRM分别为ERM和IRM训练结构下的损失函数。

为了实现自动选择权重,按照Kendall等人在文献[17]中提出的策略,将式(15)中的损失函数改写为式(16)形式:

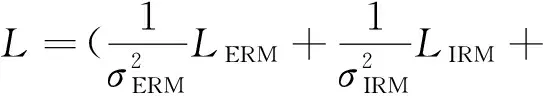
(16)

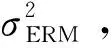
3.3 拓展至概率预测:分位数回归

模型中通过净负荷预测得到的输出是一个条件期望函数,通过函数找到当输入确定时的输出期望。分位数回归不仅是研究输出的期望值,而是希望探索输出的完整数据分布[9]。分位数回归可以直接将确定性预测模型重构为区间预测形式,以将本文策略扩展到概率预测。设原始损失函数为L(yreal,ypred),结合分位数回归得到式(17),其中q为介于(0,1)之间的分位数因子,通过控制q的取值可以得到不同分位数的上下限。

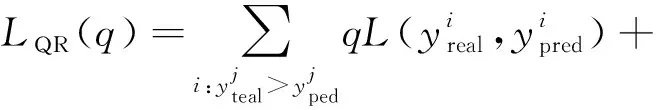
(17)

式中:LQR(q)为结合分位数后的损失函数;i和j为第i和j个数据;yreal为真实值;ypred为预测值。图5描述了基于IRM-UW-LSTM的净负荷预测方法的总体框架。

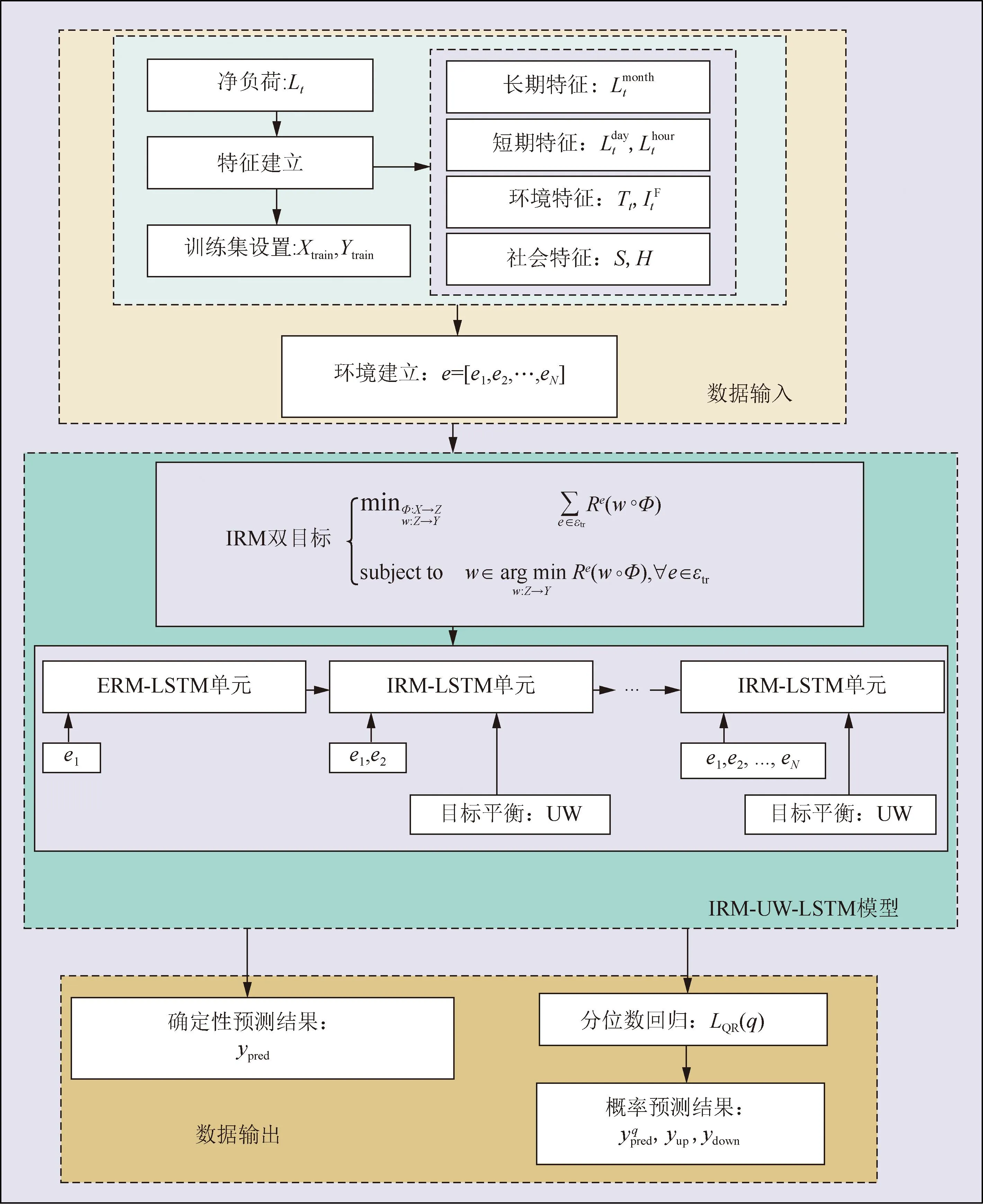
图5 基于IRM-UW-LSTM的净负荷预测整体框架Fig.5 The process of the net load forecasting method based on IRM-UW-LSTM

4 案例分析

4.1 数据集描述

本文使用澳大利亚Ausgrid公司提供的真实居民电表数据,这些数据来自悉尼数百个安装了光伏电表的用电客户,提供了2010年7月至2013年6月的半小时粒度的净负荷数据和光伏发电数据。数据的详细信息参见文献[11]。

4.2 实验细节描述

为了验证本文所提方法的有效性,本文引入了多种常用的确定性和概率预测方法作为对比。其中确定性方法采用随机森林(random forest,RF)[18-19]、LSTM[20-21]、时间卷积网络(temporal convolutional network,TCN)[22]、卷积长短期记忆神经网络(convolutional long short-term memory neural network,CNNLSTM)[23]。概率预测比较方法采用分位数RF(quantiles-RF, QRF)[19]、分位数LSTM(quantiles-LSTM, QLSTM)[21]、分位数CNNLSTM(quantiles-CNNLSTM, QCNNLSTM)[23]。通过网格搜索和交叉验证确定的模型超参数如表2所示。所有测试算法均用Python实现,主要使用的软件包有Scikit-learn、Keras和PyTorch。

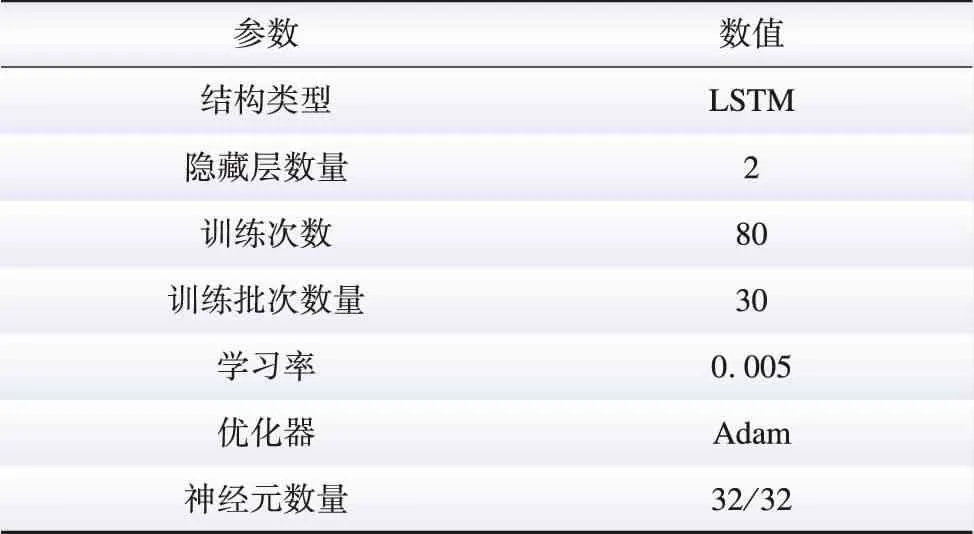
表2 超参数值Table 2 Hyperparameter value

4.3 结果评估方法

本文使用了6个评估指标来评估所研究方法的预测性能。平均绝对百分比误差(mean absolute percentage error,MAPE)、均方根误差(root mean square error,RMSE)和归一化均方根偏差(normalized root mean square deviation,NRMSD)作为确定性预测评估方法。此外,由于在光伏渗透率较高时,净负荷数据可能出现接近0的值,此时MAPE的可靠性会受到影响。为了更好地克服这一问题,引入了平均反正百分误差(mean arctangent absolute percentage error,MAAPE)[24]。将Pinball和Winkler score[1]作为概率预测评估方法。评价指标的表述如下详述。

1)确定性预测指标。

计算MAPE和MAAPE的目的是量化实际净负荷与预测净负荷数据之间的绝对差异,同时全面衡量模型预测结果的好坏[25]。计算公式如下:

(18)

(19)

式中:ytest,i为实际净负荷;ypred,i为预测净负荷。

RMSE用来评估预测结果中极大或极小误差的敏感性,表示如下:

(20)

NRMSE提供了归一化的预报精度,其解释性更强,可以对不同尺度的预测结果进行比较,表示如下:

(21)

式中:D为数据的最大值和最小值之差。MAE、MAPE、MAAPE、RMSE和NRMSD值越小,预测结果越准确。

2)概率预测的指标。

Winkler score在关注区间宽度的同时,可以很好地衡量无条件覆盖率,是概率预测中的一个综合评价指标。它可以表示为:

(22)

式中:yup和ydown为预测区间的上限和下限;δ=yup-ydown为预测区间的宽度;1-α为置信水平。Winkler score的值越小越好。

Pinball是另一种综合概率预测评估指标,可表示如下:

(23)

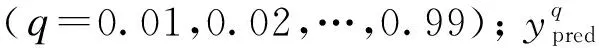
4.4 确定性预测结果

本节的目标是将本文提出的方法与常用的确定性预测方法的预测结果进行比较。证明本文方法具有更高的确定性预测精度。不同方法下评估指标如表3所示。本文提出的IRM-UW-LSTM方法的各项评估指标MAE、MAPE、MAAPE、NRMSD和RMSE值都是最低的,说明本文提出的方法具有最高的预测精度。4项指标的误差分别比次优方法CNNLSTM降低了9.36%、7.36%、11.74%和11.81%。同时,从表3还可以看出,传统人工智能方法RF的误差较大,而基于深度学习技术的LSTM、TCN方法以及组合预测方法CNNLSTM的误差次之,这说明了数据分布偏移对现有各种类型人工智能的预测方法都有一定的影响。图6给出了不同方法的确定性预测结果,可以观察到本文提出的方法更接近实际值。这表明本文所提方法具有更高的净负荷预测精度。

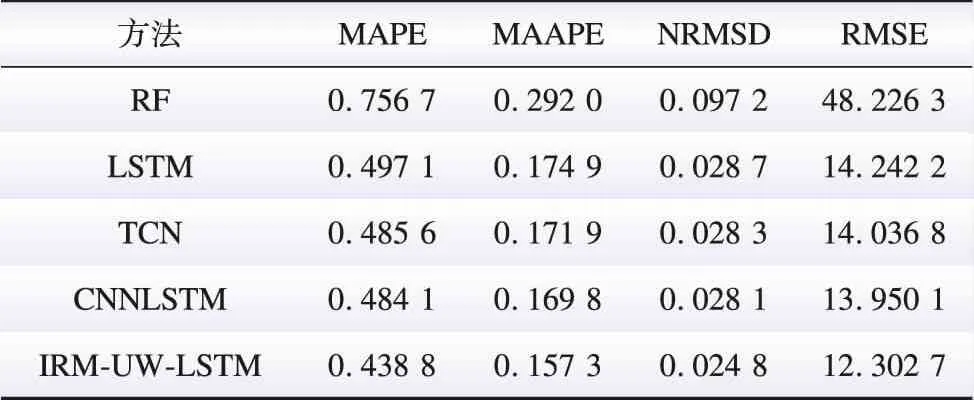
表3 确定性净负荷预测结果Table 3 Deterministic net load forecasting results

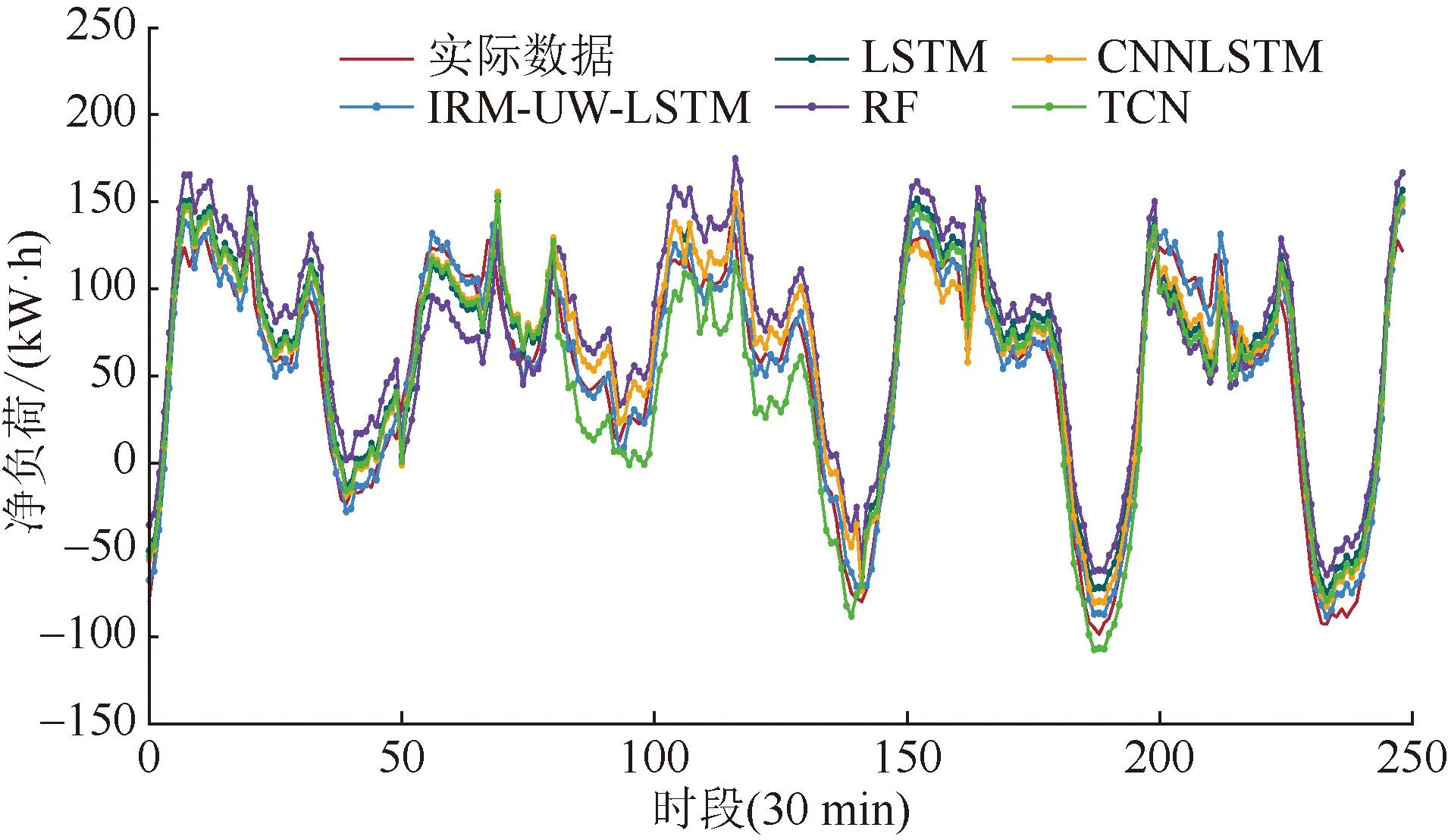
图6 不同方法下确定性净负荷预测结果Fig.6 Deterministic net load forecasting results under different methods

4.5 概率预测结果

本节的目标是将本文提出的方法与常用的概率预测方法的预测结果进行比较,以证明本文方法具有更高的概率预测精度,如图7所示。图7中,红线代表实际净负荷,蓝色由浅到深分别代表50%和90%的置信区间。通过比较图7(a)、(b)、(c)、(d)可以直观地看出,本文提出的方法在90%置信区间具有更紧密的预测覆盖区间,在50%置信区间也有一定的精度提升幅度。不同方法下的概率预测评估指标如表4所示,本文所提方法的Winkler score和Pinball值最低。对于更关注无条件覆盖率和区间宽度的指标Winkler score,与次优方法CNNLSTM相比,所提方法的误差在置信水平50%和90%下分别减少了15.74%和9.34%。而对于指标Pinball,所提方法的误差降低了10.69%。这表明本文所提方法具备更高的概率净负荷预测精度,证明了将本文方法扩展到概率预测的可能性。

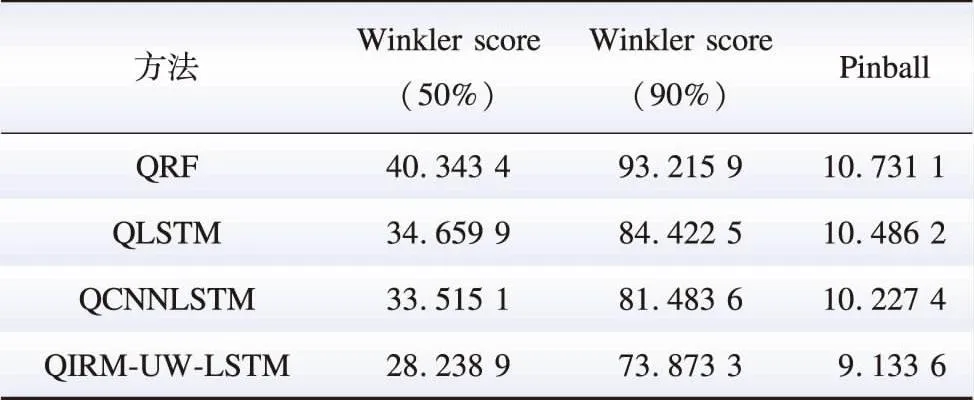
表4 不同方法下概率净负荷预测评估结果Table 4 Probabilistic net load forecast evaluation results under different methods

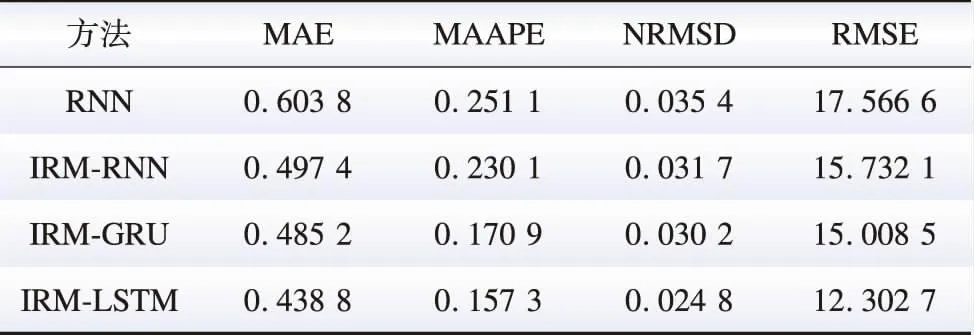
表5 不同RNN网络的净负荷预测结果Table 5 Net load forecasting results for different RNN networks

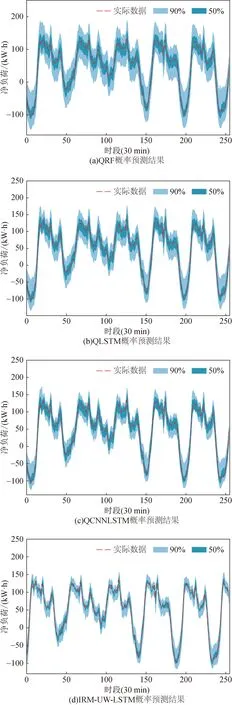
图7 净负荷概率预测结果Fig.7 Probabilistic net load forecasting results

4.6 不同程度数据分布偏移预测结果

为了更好地体现本文所提方法在净负荷预测过程中应对数据分布偏移的能力,本节验证在面对不同程度的数据分布偏移时所提方法的有效性。以2013年1月至6月的数据作为测试集。图8给出了在不同数据分布偏移程度下本文所提方法与次优方法CNNLSTM的MAAPE和RMSE。本文提出的方法在各个月份下的误差总体上低于次优方法。所提方法相比次优方法误差指标提升程度如图9所示。分别观察2013年1-6月数据分布偏移程度以及各月份精度的提高程度。两种方法下指标的变化趋势一致,这表明,数据分布偏移程度由小到大的顺序,也就是准确度相对提高程度由小到大的顺序,反映出本文提出的方法在面对较大的数据分布偏移时具有较好的改进潜力。相比之下,数据分布偏移程度越小,本文所提方法精度提高的程度也越小。

图9 不同数据分布偏移程度下所提方法与次优方法相比MAAPE、RMSE的提升程度Fig.9 Relative improvement of proposed method compared to the second-best method under different degrees of data distribution shift

4.7 不同光伏渗透率预测结果

可再生能源发电的间歇性和不确定性是净负荷数据分布偏移的主要原因之一。可再生能源渗透率越高,数据不确定性越大,数据分布偏移程度越高。所有用户的总用电量、光伏发电量和净负荷数据已知,可以通过控制无光伏发电量客户的数量来控制光伏渗透率。假设一些客户的光伏发电量为0(即这些客户的用电量全部由净负荷提供)。本文以300个客户为固定值,构建(0,300)、(50,250)、(100,200)、(150,150)、(200,100)、(250,50)、(300,0)的实验组,其中前者为无光伏发电出力的用户数量,后者为有光伏发电的用户数量。图10给出了不同光伏渗透率下所提方法与次优方法的MAAPE和RSME。从图10可以看出,光伏用户越多,即光伏渗透率越高,评价指标MAAPE和RMSE的值越大。这与数据分布偏移越明显,预测难度越大、精度越差的结论一致。此外,光伏渗透率越高,本文所提方法的精度提升程度越大,当渗透率最高时,改进幅度分别为16.062%和13.452%。本节仿真结果说明,光伏渗透率越高,数据分布偏移程度越高,本文所提方法的精度提升程度越大。这与第4.6节的结论是一致的,也反映出随着未来光伏等新能源在电力系统中渗透率的提高,本文方法具有较大的应用潜力。

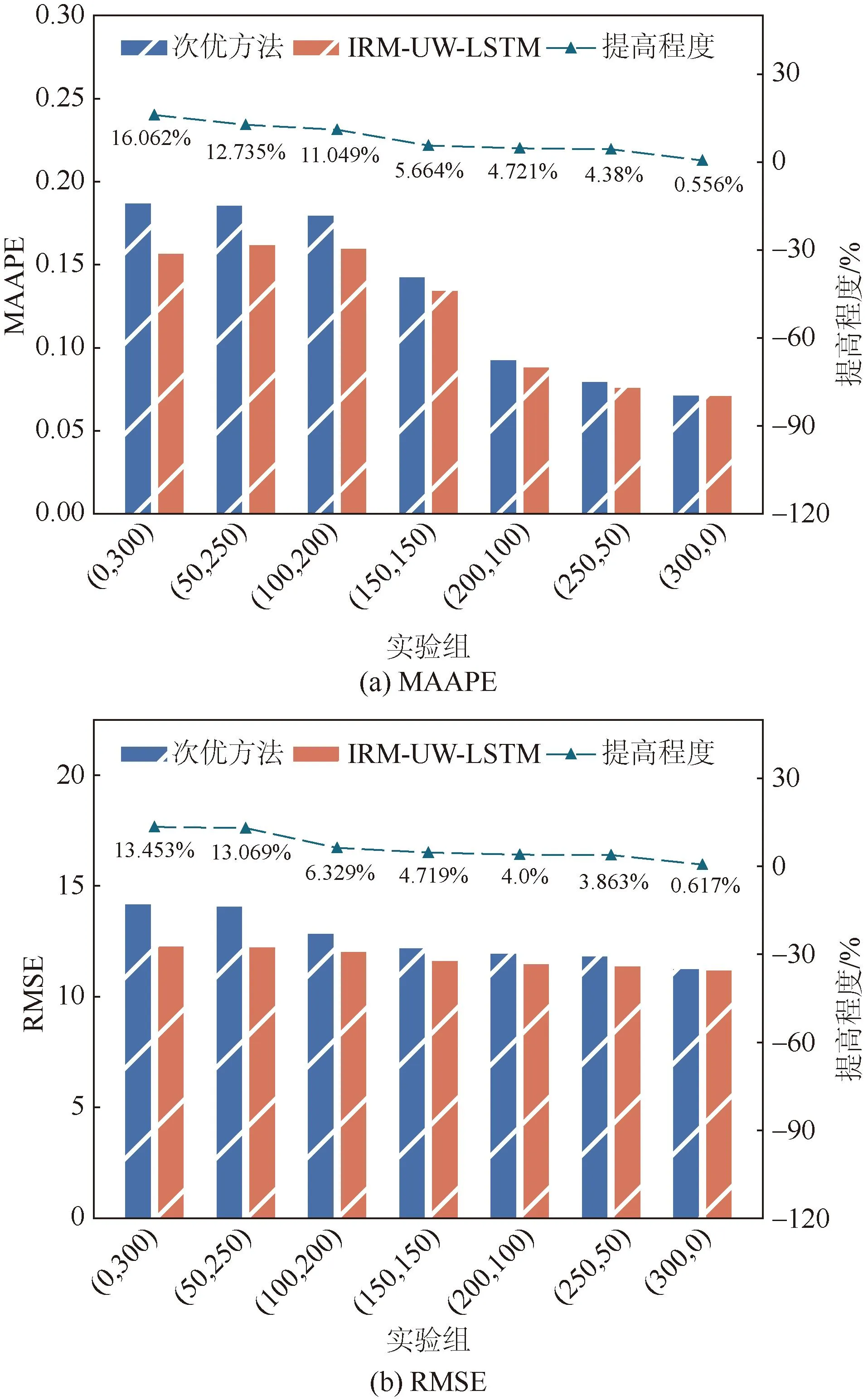
图10 不同光伏渗透率下所提方法与次优方法的MAAPE、RMSE结果Fig.10 MAAPE and RMSE results of the proposed method and the suboptimal method under different photovoltaic permeability

4.8 不同RNN网络结构预测结果

RNN因其处理连续数据的能力而广泛应用于负荷预测。RNN的网络机制使模型能够将上一时间步产生的结果作为当前时间步输入的一部分,从而影响当前时间步的输出。在负荷预测领域几种常见的RNN变体如:LSTM[21]、门控循环单元(gate recurrent unit,GRU)[26],它们除了继承了RNN的优良预测特性外,还能更好地处理更长的时间序列数据,同时克服梯度爆炸等问题[27]。本节比较了IRM-RNN、IRM-LSTM和IRM-GRU的预测结果,结果表明在利用本文所提方法克服净负荷数据分布偏移时,LSTM是更优的选择。表5给出了不同RNN网络的净负荷预测结果,可知,IRM-LSTM具有更好的预测精度,与IRM-RNN和IRM-GRU相比,MAAPE分别提高了31.6%和7.96%。由于张量运算较少,GRU的计算速度更具优势。表6给出了不同RNN网络计算时间,从表6可以看出,IRM-GRU在训练时间方面更占优势。结果表明,IRM并没有改变RNN网络本身的优势,这进一步说明了本文方法的合理性,同时,未来可以根据预测需要选择更快或更准确的方法。

表6 不同RNN网络的计算时间Table 6 Computational time for different RNN network

5 结 论

由于更多不确定性的注入,分布式能源的广泛部署大大降低了净负荷的可预测性。更高的不确定性使得净负荷数据分布偏移更为频繁和严重。针对此问题,本文通过学习不同净负荷数据分布下的不变特征信息,提出了一种基于IRM-UW-LSTM的短期居民净负荷预测方法。该方法不同于现有方法,减少了模型对测试集与训练集数据独立同分布的依赖。通过Ausgrid公司提供的真实净负荷数据验证了本文方法可以通过克服数据分布偏移问题提高确定性和概率净负荷预测精度。而且,结果表明,分布偏移程度越高,该方法与其他方法相比改进潜力越大。此外,随着可再生能源在电力系统中渗透率的提高,本文方法具有更高的应用潜力。