直驱风电场经柔直送出系统近工频正/负序振荡机理分析

于婧, 林鸿飞,王潇,吕敬,吴林林,李蕴红

(1. 国家电网有限公司国家电力调度控制中心,北京市 100052;2. 电力传输与功率变换控制教育部重点实验室(上海交通大学),上海市 200240;3. 国网冀北电力有限公司电力科学研究院,北京市 100045)

0 引 言

近年来,以风电、光伏为代表的新能源迅猛发展,柔性直流输电成为大规模新能源直流外送的主流方案之一[1]。然而,随着新能源柔直送出工程的不断建设,各类振荡现象频发,严重影响了新能源并网消纳和电网安全稳定运行。目前国内已投运的新能源柔直送出工程基本均出现了不同频段的振荡现象,如南澳风电柔直工程出现20～30 Hz次同步振荡[2-3]、张北新能源柔直工程出现2～6 Hz次同步振荡[4]和750～3 550 Hz中/高频振荡[5]、如东海上风电柔直工程出现320 Hz、2 000 Hz和2 500 Hz中/高频振荡[6-7]等。此外,近期张北新能源柔直工程还发生了44 Hz/56 Hz正序和58 Hz负序近工频振荡现象,振荡机理尚不明晰。

目前国内外针对风电柔直送出系统的振荡稳定性问题已开展一定研究,研究对象包括风电经两电平电压源型高压直流(voltage-source converter based high-voltage direct current,VSC-HVDC)并网系统和风电经模块化多电平换流器高压直流(modular multilevel converter based HVDC,MMC-HVDC)并网系统。针对风电经两电平VSC-HVDC并网系统,文献[8-10]采用特征值分析法分别研究了双馈和直驱风电场经VSC-HVDC并网系统的次同步振荡特性,指出该次同步振荡是由风电机组网侧变流器直流电压控制环节产生的正反馈环路诱发的;文献[11-12]建立了全功率风电机组经柔直并网系统的状态空间模型,通过参与因子分析研究了影响系统振荡的主要因素。此外,文献[13-15]利用阻抗法揭示了直驱和双馈风电场经VSC-HVDC送出系统的次同步振荡机理,指出风电场与柔直送端换流器在特定频段内构成负电阻的虚拟电感-电容谐振电路,进而引发互联系统次同步振荡现象。

实际上,自2010年以后国内外建设投运的柔直工程均采用MMC拓扑,其交流侧输出特性与两电平VSC有较大区别,因此其振荡机理也有所不同。文献[16-20]基于谐波状态空间法建立了考虑内部谐波动态的柔直MMC详细阻抗模型,指出柔直送端MMC的内部动态特性是导致风电-柔直互联系统产生次同步振荡的主要原因之一,并且分析了不同控制环节、控制结构、能量控制等对风电-柔直并网系统次同步振荡的影响。文献[21-22]建立了考虑频率耦合的MMC多维阻抗模型,并给出了在风电-柔直交互稳定性分析中的降维方法。文献[23]建立了考虑直流侧动态的柔直送端MMC阻抗模型。此外,文献[24-26]利用阻抗法分析了风电柔直送出系统的高频振荡机理,指出柔直送端MMC的控制延时引入的高频负电阻特性是引发风电柔直送出系统高频振荡的主要原因;文献[6]研究表明风电柔直送出系统的中频振荡除了受控制延时的影响,还受到风电机组和柔直送端换流器的闭环控制等因素的影响,其作用机理和影响规律更加复杂。

需要指出的是,现有研究仅考虑风电机组和柔直MMC的正序控制,主要关注的是正序振荡问题,而实际的风电机组和柔直换流器往往含有负序控制环节,有可能产生负序振荡风险(如张北工程近期出现的58 Hz负序振荡现象),目前对于风电柔直送出系统的负序振荡特性与关键影响因素及其影响规律尚不明确。

为此,本文针对直驱风电场经柔直送出系统的近工频正/负序振荡问题开展深入研究。首先,基于谐波状态空间建模方法建立计及负序控制的直驱风电机组和柔直送端MMC的精细化阻抗模型,然后从阻抗特性角度揭示直驱风电场与柔直送端MMC换流站间近工频正序和负序振荡的产生机理;其次,基于参数相位裕度灵敏度指标定量提取近工频正/负序振荡的关键影响因素;然后,通过绘制相位裕度灵敏度-参数-频率特性和最小相位裕度-参数-频率特性曲线,分析直驱风电场与柔直送端MMC间控制交互对近工频段正/负序振荡稳定性的影响;最后,通过时域仿真复现实际系统的近工频正/负序振荡现象,并验证振荡机理分析的正确性。

1 直驱风电机组和柔直送端MMC的精细化阻抗建模

1.1 直驱风电场经柔直送出系统结构

直驱风电场经柔直送出系统结构示意图如图1所示(仅展示送端系统)。风电场由200台永磁直驱风电机组构成,通过风电场升压变和输电线路接入柔直送端MMC的换流变,然后经过柔直送端MMC整流成直流电,送至柔直受端MMC换流站。为简化分析,风电场采用单机等值聚合模型[27]。此外,由于风电场到柔直送端换流站的距离一般较短,输电线路的分布电容对本文所关注的近工频段振荡影响较小,因此在建模中忽略输电线路分布电容的影响,仅考虑线路电阻和电感。

1.2 直驱风电机组的精细化阻抗建模

直驱风电机组的典型拓扑与控制结构如附录A图A1所示。直驱风机的机侧换流器(machine-side converter,MSC)采用转矩控制,网侧换流器(grid-side converter,GSC)外环采用定直流电压和无功功率控制,内环采用正负序电流控制。同时,配备了正负序分离算法,锁相环(phase-locked loop, PLL)采用普通锁相环(synchronous rotating frame PLL,SRF-PLL),上述控制的具体参数和结构如附录A图A2、图A3所示。其余各参数如附录B表B1所示。

直驱风电机组阻抗建模的基本思路与文献[28]类似,通过推导交流侧端口电压usabc与电流isabc之间的关系,得到交流侧端口阻抗。与之不同的是,本文采用谐波状态空间(harmonic state-space,HSS)建模方法[18],建立计及负序控制和正负序分离算法的直驱风电机组交流侧阻抗模型。

交流侧三相谐波阻抗的表达形式如下:

(1)

(2)

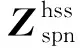
从式(2)中提取二维改进序阻抗Zspn,其表达式为:

(3)

式中:Zspp、Zsnn、Zspn、Zsnp分别代表改进序阻抗矩阵的四个元素,其中Zspp表示正序阻抗,Zsnn表示负序阻抗,Zspn和Zsnp表示正、负序间的耦合阻抗。

进一步通过阻抗降维方法[29-30]得到等效单维正序阻抗Zsp和负序阻抗Zsn:

(4)

1.3 柔直送端MMC的精细化阻抗建模

柔直送端MMC换流器拓扑结构如附录A图A4所示,MMC由三个相单元构成,每相分为上桥臂和下桥臂,每个桥臂包含N个子模块、一个等效电感Larm和一个电阻Rarm。

在孤岛运行模式下,柔直送端MMC换流器采用定交流电压控制来维持公共耦合点(point of common coupling, PCC)电压恒定,为风电场提供稳定的交流电压源。MMC换流器的控制结构如图2所示,包含正负序交流电压外环、正负序电流内环、二倍频环流抑制器(circulating current suppressing controller,CCSC)、正负序分离等控制环节。图2中:下标 a、b、c 表示各变量在abc三相静止坐标系下的分量;下标d、q表示各变量在dq旋转坐标系下的分量;下标+、-分别表示正、负序分量;Hvp、Hvn、Hip、Hin、Hccsc分别表示MMC正序交流电压外环、负序交流电压外环、正序电流内环、负序电流内环、CCSC的PI控制器传递函数;Td为控制延时;Ugdref+、Ugqref+和Ugdref-、Ugqref-,vgd+、vgd-和igq+、igq-分别为正、负序交流电压参考值和实际值的d、q轴分量;igdref+、igqref+和igdref-、igqref-,igd+、igd-和igq+、igq-分别为正、负序交流电流参考值和实际值的d、q轴分量;vsdref+和vsqref+、vsdref-和vsqref-分别为基频正、负序调制参考电压的d、q轴分量;vcdref、vcqref分别为二倍频调制参考电压的d、q轴分量;vsxref+、vsxref-、vcx(x=a、b、c,表示三相)代表三相静止坐标系下调制参考电压。

MMC的单相平均等效电路如附录A图A5所示。基于上述控制结构,选取MMC桥臂环流、上下桥臂子模块电容电压、交流侧输出电流作为状态变量,基于MMC单相平均等效电路和基尔霍夫定律,可得到MMC的时域状态空间模型:

(5)

式中:icomx、ucuxΣ、uclxΣ、igx、vgx、mux和mlx分别代表桥臂环流、上桥臂子模块电容电压之和、下桥臂子模块电容电压之和、交流侧电流、交流侧电压、上桥臂调制函数和下桥臂调制函数,其均为三相周期时变信号,包含多次谐波分量;Δ表示对应变量的小信号分量,上标“s”表示对应变量的稳态分量,也为周期性时变信号,例如:子模块电容电压之和的稳态量中主要含有直流、基频、二倍频以及三倍频等分量;Carm代表桥臂等效电容。

调制比Δmux和Δmlx的小信号模型如下所示:

(6)

进一步地,上、下桥臂调制信号的小信号可表示为状态变量的小信号形式:

(7)

式中:T1(s)、T2(s)和T3(s)均可以通过图2的控制结构推导得到,其具体表达式见附录C式(C1)-(C3)所示。

将式(7)代入式(5),消去中间变量,即可得到MMC在正负序电压电流双闭环控制下的谐波状态空间方程:

(8)

将Xp以矩阵的形式展开有:

(9)

提取导纳并按谐波顺序排列,可以得到扰动频率处的三相谐波阻抗为:

(10)

1.4 阻抗模型验证

为验证上述阻抗模型的正确性,在Matlab/Simulink中搭建直驱风电机组和柔直送端MMC的仿真模型,通过扫频测量两者的交流侧阻抗,直驱风电机组和柔直送端MMC主电路和控制参数如附录B表B1和表B2所示。理论阻抗和仿真测量阻抗的对比如图3和图4所示,从图中可以看出,在1～100 Hz范围内两者具有较高的吻合度,验证了理论阻抗模型的准确性。

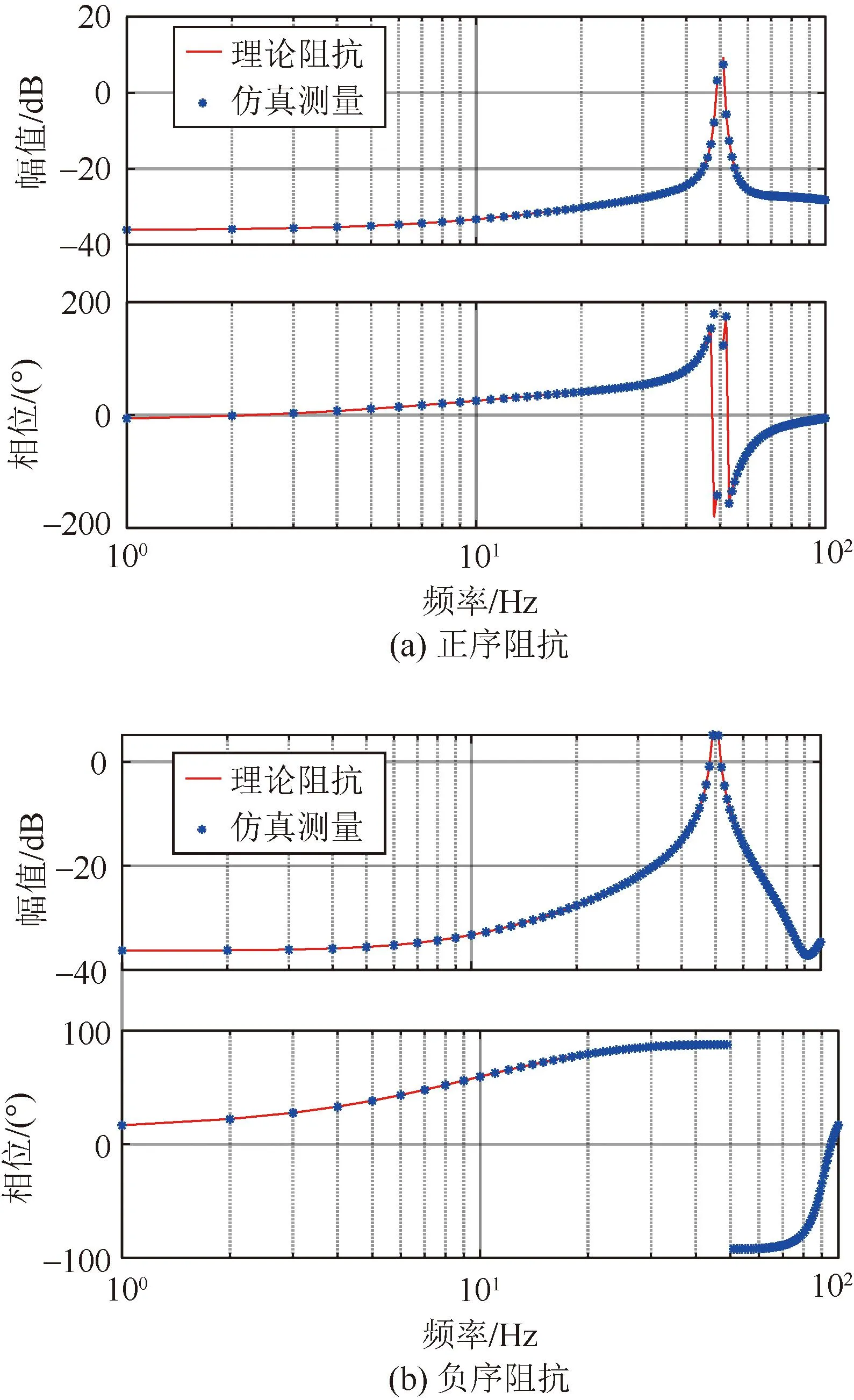
图3 直驱风机阻抗模型验证Fig.3 Validation for the impedance model of direct-drive wind turbine

图4 柔直送端MMC阻抗模型验证Fig.4 Validation for the impedance model of sending-end MMC of MMC-HVDC

2 近工频正/负序振荡机理及影响因素分析

2.1 近工频正/负序振荡机理分析

基于前文建立的直驱风电机组和柔直送端MMC的正/负序阻抗模型,首先分析不同控制环节对直驱风电场和柔直MMC近工频正负序阻抗特性的影响,分析结果见附录D;进一步地,从阻抗特性角度分别揭示直驱风电场与柔直送端MMC换流站间产生近工频正序和负序振荡的机理及关键影响因素。

2.1.1 近工频正序振荡机理

本节设计研究案例1:风电场总体出力为0.7 pu,风电机组及升压变参数见附录B表B1, 柔直送端MMC及换流变的参数见附录B表B2。在本组参数下,直驱风电场与柔直送端MMC换流站的近工频段正/负序阻抗特性曲线分别如图5(a)和图5 (b)所示。从图5中可以看出,直驱风电场与柔直送端MMC换流站的正序阻抗幅频曲线在44 Hz和56 Hz处相交,且对应频率处的相位裕度小于0,表明互联系统存在44 Hz和56 Hz近工频正序振荡风险。此外,直驱风电场和柔直送端MMC换流站的负序阻抗幅频曲线在41 Hz和58 Hz处相交,但对应的相位裕度均大于0,表明互联系统不存在近工频负序振荡风险。

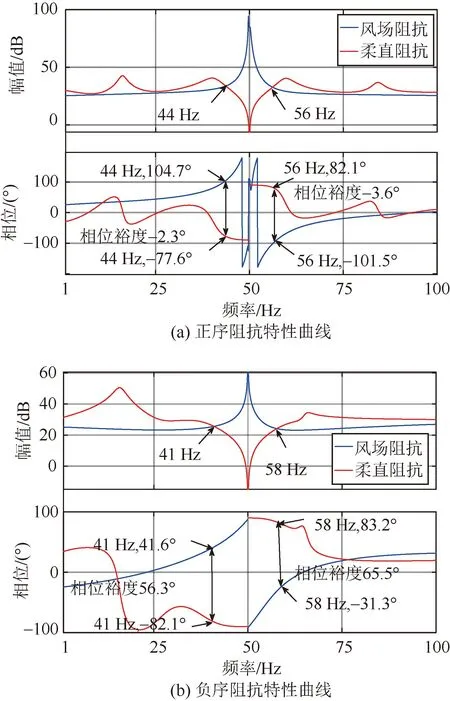
图5 直驱风电-柔直互联系统近工频正序振荡机理分析Fig.5 Near fundamental-frequency positive-sequence oscillation mechanism of the PMSG-based wind farm-MMC interconnected system

由互联系统正序阻抗特性曲线可以看出,在次同步近工频段,直驱风电场由于正序电流控制作用主要呈现感性,且越接近工频,感性越强,并呈现较强的负电阻特性;柔直送端MMC换流站由于正序电流控制作用,工频附近存在谐振峰,且越接近工频,容性越强。因此,直驱风电场与柔直送端MMC间次同步近工频正序振荡机理为:直驱风电场在近工频段较强的负电阻感性特性与柔直送端MMC换流站的容性特性相互作用,易诱发次同步近工频正序振荡。在超同步近工频段,直驱风电场由于控制作用主要呈现容性,且越接近工频,容性越强,并呈现较强的负电阻特性;柔直送端MMC换流站由于正序电流控制作用,工频附近存在谐振峰,且越接近工频,感性越强。因此,直驱风电场与柔直送端MMC间超同步近工频正序振荡机理为:直驱风电场在近工频段较强的负电阻容性特性与柔直送端MMC换流站的感性特性相互作用,易诱发超同步近工频正序振荡。

2.1.2 近工频负序振荡机理

本节设计研究案例2:风电场总体出力为0.4 pu,风电机组及升压变参数见附录B表B1,柔直送端MMC及换流变的参数见附录B表B2。在本组参数下,直驱风电场与柔直送端MMC换流站的近工频段正/负序阻抗特性曲线分别如图6(a)和图6 (b)所示。从图6中可以看出,直驱风电场与柔直送端MMC换流站的负序阻抗幅频曲线在59 Hz处相交,且对应频率处的相位裕度小于0,表明互联系统存在59 Hz超同步负序振荡风险;而在41 Hz交点频率处的相位裕度大于0,表明系统不会产生41 Hz的次同步负序振荡。此外,由正序阻抗特性曲线可以看出,直驱风电场与柔直送端MMC间在次/超同步频段的相位裕度均大于0,表明互联系统不存在次/超同步正序振荡风险。

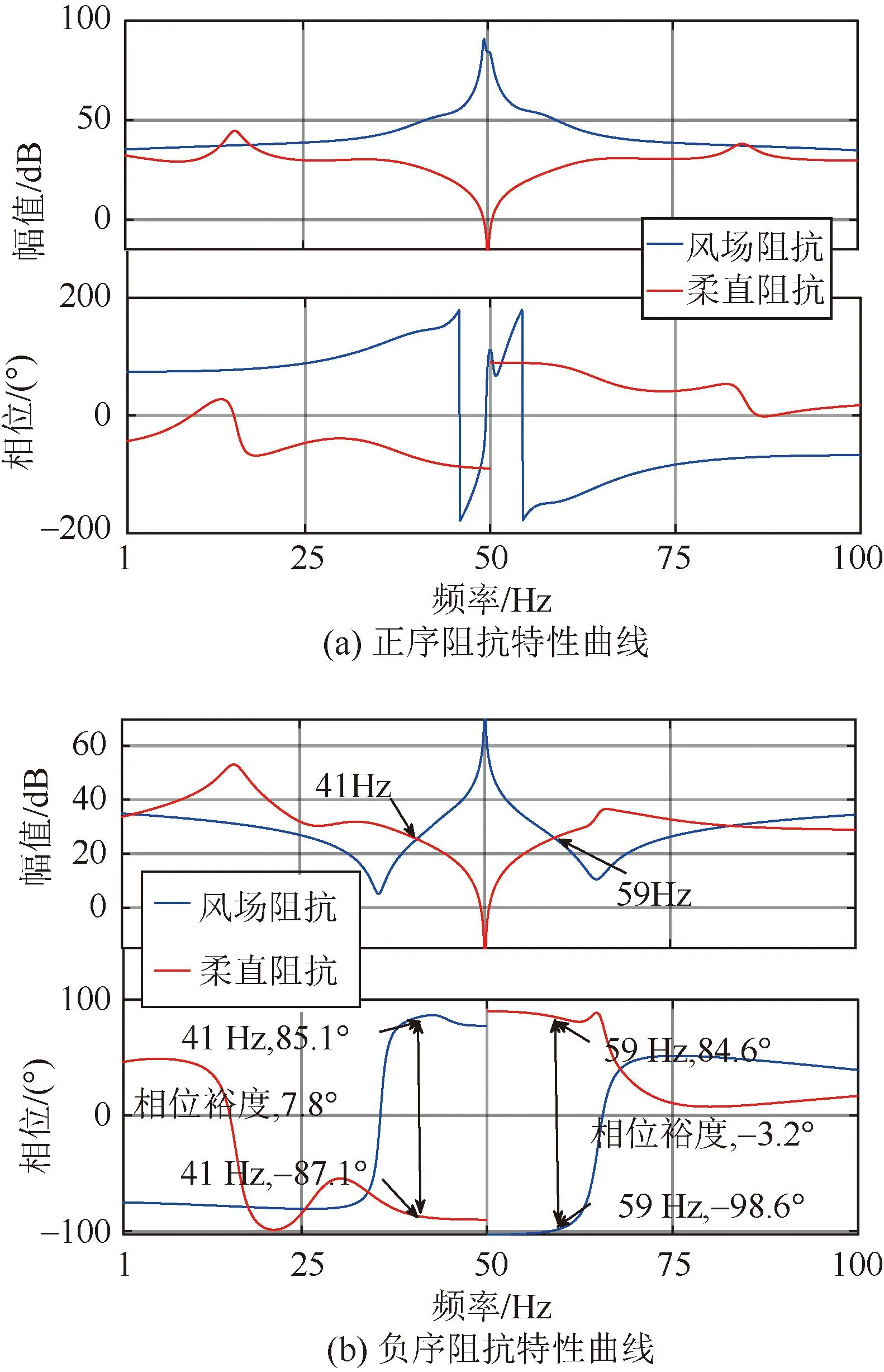
图6 直驱风电-柔直互联系统近工频负序振荡机理分析Fig.6 Near fundamental-frequency negative-sequence oscillation mechanism of the PMSG-based wind farm-MMC interconnected system

由互联系统负序阻抗特性曲线可以看出,在次同步近工频段,直驱风电场由于负序电流控制作用主要呈现感性,柔直送端MMC越接近工频容性越强。振荡机理为:风电场在工频附近较强的感性与柔直送端MMC的容性特性相互作用,易诱发次同步近工频负序振荡。在超同步近工频段,直驱风电场由于电流控制作用主要呈现容性,且越接近工频容性越强,并呈现较强的负电阻特性;柔直送端MMC由于负序控制环节作用呈现感性。因此,直驱风电场与柔直送端MMC间超同步近工频负序振荡机理为:直驱风电场在近工频段较强的负电阻容性特性与柔直送端MMC的感性特性相互作用,易诱发超同步近工频负序振荡。

2.2 近工频正/负序振荡关键影响因素分析

为分析引发互联系统近工频正/负序振荡的关键影响因素,基于近工频振荡机理分析结果,定义互联系统正/负序参数相位裕度灵敏度如下:

(11)

式中:ai为风电场或柔直MMC换流器的主电路和控制第i个参数;Δai为该参数的微增量,在本文中Δai选取ai的0.1%。将互联系统在交点频率fos处的相位裕度代入式(11)即可求得相位裕度关于参数ai的偏导数,进而定量评估某个参数在其设定值附近变化时对互联系统相位裕度的影响程度。相位裕度灵敏度越大,表示系统稳定性受该参数变化的影响越大;而相位裕度灵敏度的正/负,则表示参数在设定值附近增加时,互联系统在潜在振荡频率处的相位裕度将增大/减小,对应系统稳定性趋于改善/恶化。

进一步地,定义某一参数灵敏度占比如下:

(12)

式中:m表示共有m个参数。

2.2.1 近工频正序振荡关键影响因素分析

针对研究案例1,计算各控制参数在44 Hz处的正序相位裕度灵敏度,结果如表1所示。

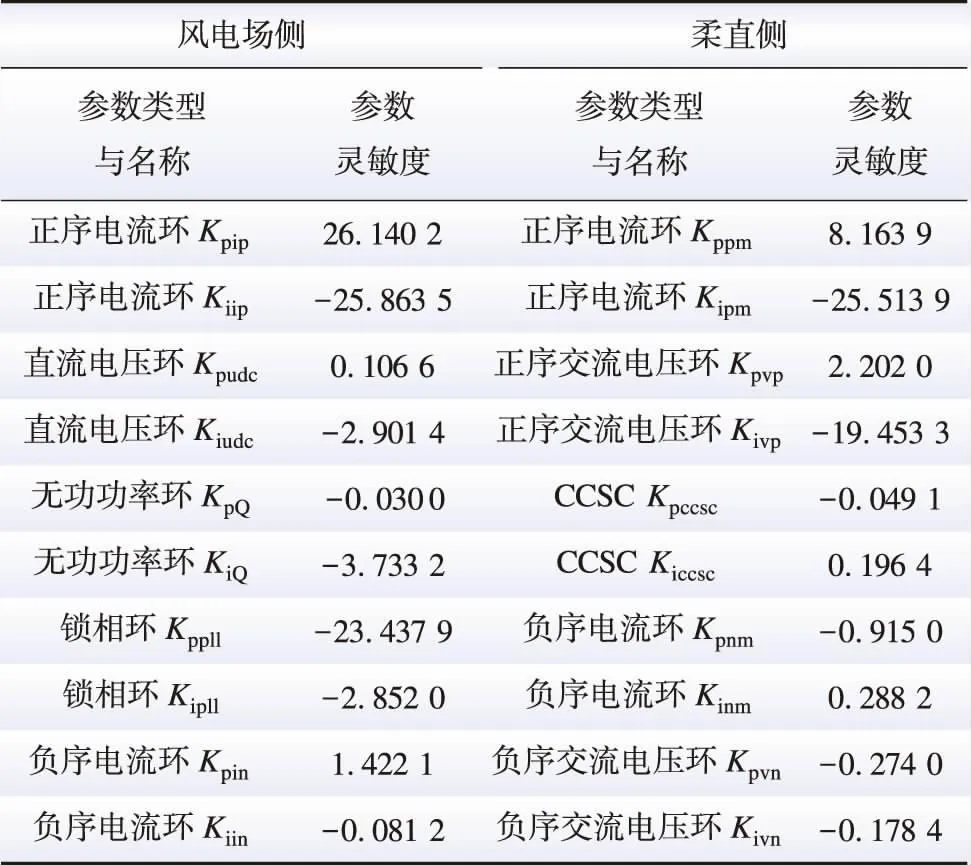
表1 正序参数相位裕度灵敏度计算结果Table 1 Calculation results of positive-sequence parameter phase margin sensitivity

图7为不同风电场出力下各参数的正序相位裕度灵敏度分析结果,由于参数较多,图中仅标注灵敏度占比较大的参数,其余参数灵敏度占比顺序按照表1风电场侧-柔直侧,从上至下的顺序排列。此外需要说明的是,当风电场出力变化时,互联系统的潜在振荡频率fos也发生变化,因此后文的分析是基于不同出力下不同fos得到的结果。

图7 不同风电场出力下正序相位裕度灵敏度占比分析结果Fig.7 Analysis results of positive-sequence phase margin sensitivity ratio under different output power of wind farm

结合表1和图7,可得到各参数对互联系统近工频正序振荡稳定性影响的结论:

1) 风电场侧影响因素灵敏度最大的是正序电流环的比例(正相关)和积分系数(负相关)。此外,锁相环的比例系数影响也较大(负相关)。

2) 风电场出力变化对互联系统正序灵敏度占比

的影响不大。随着风电场出力的增加,正序电流环比例系数影响的正相关程度略微减弱,积分系数影响的负相关程度略微增强,锁相环比例系数影响的负相关程度有所增强。

3) 柔直送端MMC侧影响因素灵敏度最大的是正序电流环的积分系数(负相关),其次是正序交流电压环的积分系数(负相关)。

综上分析,风电场侧和柔直送端MMC侧正序控制参数对近工频正序振荡稳定性影响的灵敏度总体上大于负序控制参数,且参数灵敏度占比受风电场出力变化的影响较小。

2.2.2 近工频负序振荡关键影响因素分析

与前文分析思路类似,针对研究案例2,计算各参数在59 Hz处的负序相位裕度灵敏度,结果如表2所示。图8为不同风电场出力下各参数的负序相位裕度灵敏度分析结果。

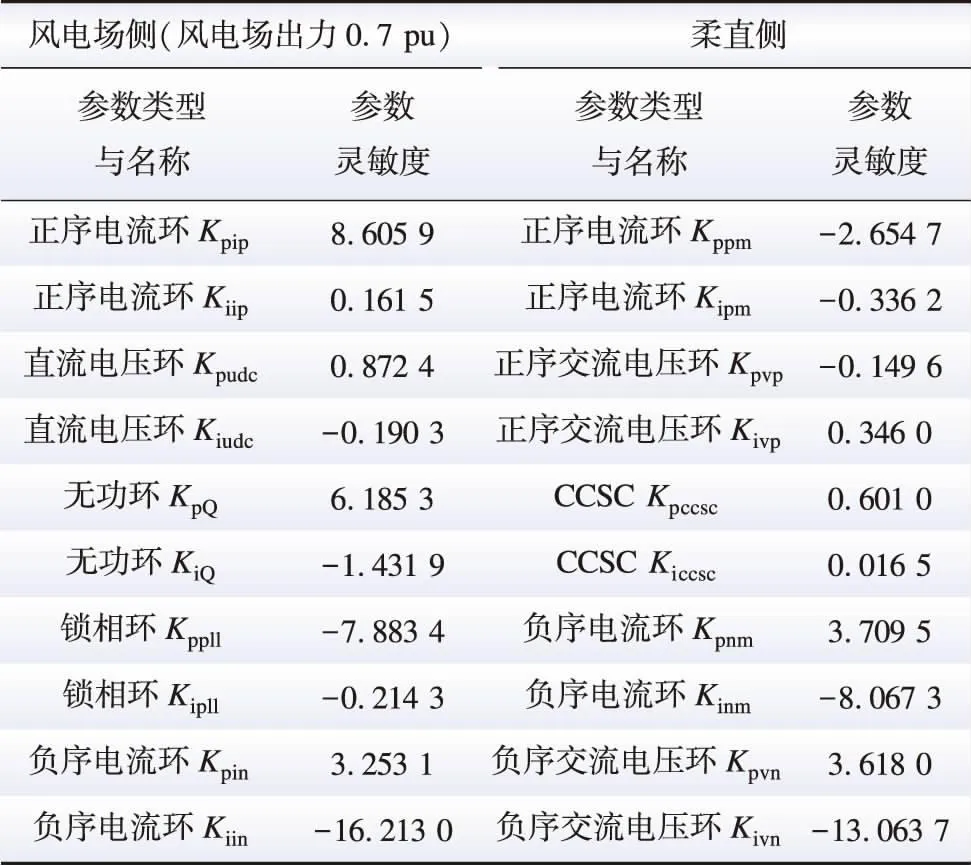
表2 负序参数相位裕度灵敏度计算结果Table 2 Calculation results of negative-sequence parameter phase margin sensitivity

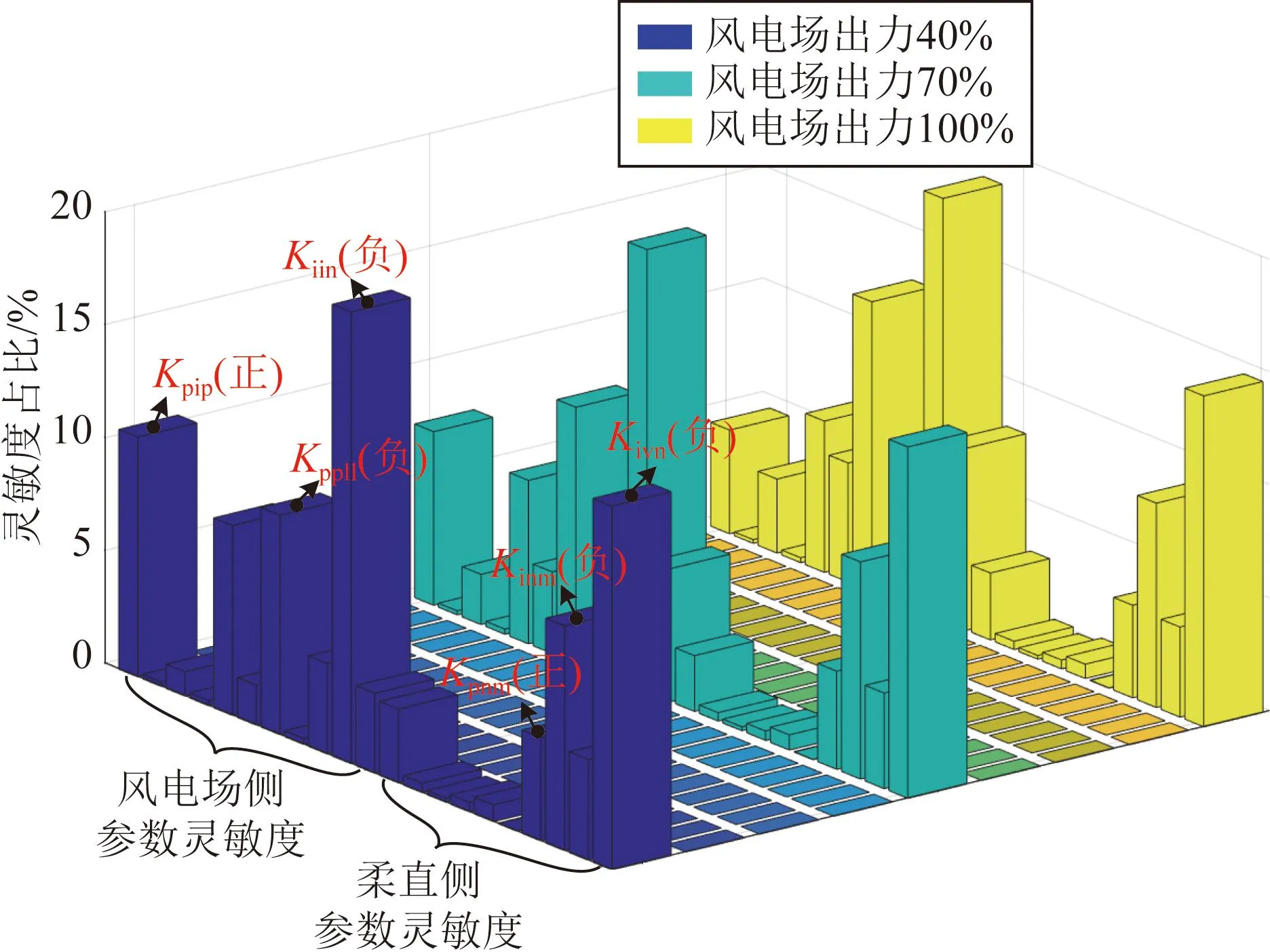
图8 不同风电场出力下负序相位裕度灵敏度占比分析结果Fig.8 Analysis results of negative-sequence phase margin sensitivity ratio under different output power of wind farm

结合表2和图8,可得到各参数对互联系统近工频负序振荡稳定性影响的结论:

1) 风电场侧影响因素灵敏度最大的是负序电流环的积分系数(负相关),其次是锁相环的比例系数(负相关)和正序电流环的比例系数(正相关)。

2) 随着风电场出力的增加,负序电流环积分系数的负相关程度略微增强,锁相环比例系数的负相关程度有所增强,正序电流环比例系数的正相关程度有所减弱。

3) 柔直送端MMC侧影响因素灵敏度最大的是负序交流电压环的积分系数(负相关),其次是负序电流环的积分系数(负相关)。

综上分析,风电场侧和柔直送端MMC侧负序控制参数对近工频负序振荡稳定性影响的灵敏度总体上大于正序控制参数,且风电场出力变化对负序参数灵敏度占比有一定影响,但各风电场出力下的主导影响因素不变。

值得说明的是,近工频振荡与以往研究的次/超同步振荡的差异如下:

1)风电场侧,次/超同步振荡主要受锁相环和直流电压外环的影响,且控制器的比例系数对振荡特性的影响较大[8,14,31];近工频振荡主要受电流环和锁相环的影响,在负序振荡案例中,电流环的积分系数对振荡特性的影响较大。

2)柔直MMC侧,次/超同步振荡主要受环流控制和交流电压环的影响,电压环比例系数对振荡特性的影响较大[3,14,31];近工频振荡主要受电流环和电压环的影响,且电流环和电压环的积分系数对振荡特性的影响较大。

2.3 控制交互对互联系统近工频稳定性的影响

上一节分析了风电场和柔直送端MMC单个参数变化对互联系统近工频振荡稳定性的影响程度。进一步地,本节选取风电场和柔直送端MMC控制系统中对近工频振荡稳定性影响较大的参数,分析直驱风电场与柔直送端MMC间控制交互作用对互联系统近工频正/负序振荡稳定性的影响。

2.3.1 控制交互对近工频正序稳定性的影响分析

由前文分析可知,影响互联系统近工频正序稳定性的强相关变量主要有风电机组的正序电流环参数、锁相环参数以及柔直送端MMC的正序电流环和正序交流电压环参数等,本节研究同一时间尺度控制环节交互对互联系统近工频正序稳定性的影响,即风电机组正序电流环比例系数与柔直送端MMC正序电流环比例系数间的交互(后文称交互案例1)。

控制交互分析思路如图9所示。以交互案例1为例,具体实施步骤如下:

图9 控制系统交互研究思路Fig.9 Research ideas of control system interaction

1) 以研究案例1参数为基准,分别改变风电机组正序电流环比例系数从0.8～1.2 pu变化,柔直送端MMC电流环比例系数从0.8～1.2 pu变化,计算每组控制参数下互联系统在正序近工频段最小相位裕度Ppmin以及对应的频率fPpmin。

2) 依据式(11),求解fPpmin处的相位裕度灵敏度Psenpmin,同时存储最小相位裕度Ppmin。

3) 绘制“相位裕度灵敏度-参数特性”三维图和“最小相位裕度-参数特性”三维图,分析控制交互对系统近工频正序稳定性的影响规律。

交互案例1的分析结果如图10所示。从图10(a)可以看出,交互案例1对互联系统近工频段相位裕度灵敏度整体影响不大,且均为正相关。减小风电机组正序电流环比例系数或增大柔直送端MMC正序电流环比例系数会略微增加系统近工频正序相位裕度灵敏度。从图10(b)可以看出,随着风电机组和柔直送端MMC正序电流环比例系数的增加,互联系统最小相位裕度曲线由负到正穿越相位裕度零平面,互联系统近工频正序稳定性增强。

图10 交互案例1分析结果Fig.10 Analysis results of interactive case 1

2.3.2 控制交互对近工频负序稳定性的影响分析

通过前文分析,影响互联系统近工频负序稳定性的强相关变量主要有风电机组的负序电流环参数、锁相环参数以及柔直送端MMC的负序电流环和负序交流电压环参数等。以研究案例2参数为基准,选取风电机组锁相环比例系数与柔直送端MMC负序交流电压环积分系数研究两者交互(后文称交互案例2)对系统近工频负序稳定性的影响,分析结果如图11所示。从图11(a)中可以看出,随着风电机组锁相环比例系数的增加,相位裕度灵敏度负相关程度逐渐增强,随着柔直送端MMC负序交流电压环积分系数的增加,相位裕度灵敏度负相关程度减弱。从图11(b)中可以看出,交互案例2对互联系统负序近工频段最小相位裕度的影响不大,且主要受锁相环比例系数的影响,随着风电机组锁相环比例系数的增加,互联系统最小相位裕度曲线由正到负穿越相位裕度零平面,互联系统近工频负序稳定性降低。

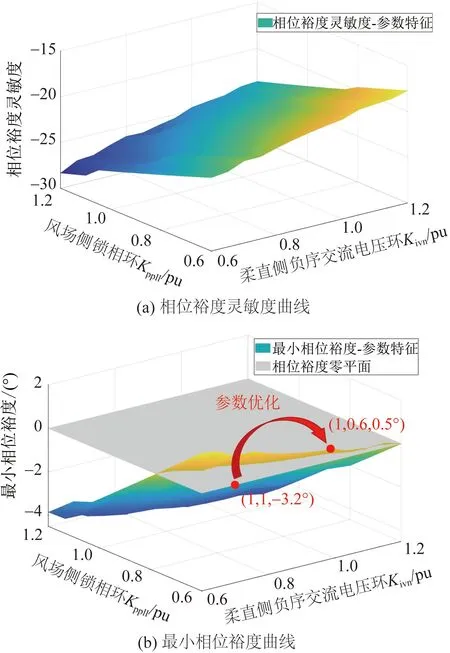
图11 交互案例2分析结果Fig.11 Analysis results of interactive case 2

3 仿真验证与分析

3.1 近工频正/负序振荡复现

针对前文设计的研究案例1和2,基于Matlab/Simulink搭建直驱风电场柔直并网系统的仿真模型,仿真参数与前文机理分析保持一致,对前文近工频正/负序振荡机理分析结果进行验证。

1)仿真案例1:近工频正序振荡。

仿真中风电场出力逐渐增加,在0.2 s时到达70%的额定功率,互联系统的PCC电压和电流时域仿真波形如图12所示。由前文理论分析可知,互联系统在此工况下,44 Hz和56 Hz处的相位裕度分别为-2.3°和-3.6°,相位裕度为负且接近于0,说明系统负阻尼特性较弱,系统表现为经过一定时间后逐渐失稳现象。仿真中,从图12(a)中可以看出,当风电场达到设定出力后,系统在1.8 s左右逐渐出现振荡现象,PCC电流的傅里叶分析结果如图12(b)所示,其振荡频率为44 Hz和56 Hz,时域仿真结果与图5的理论分析一致。

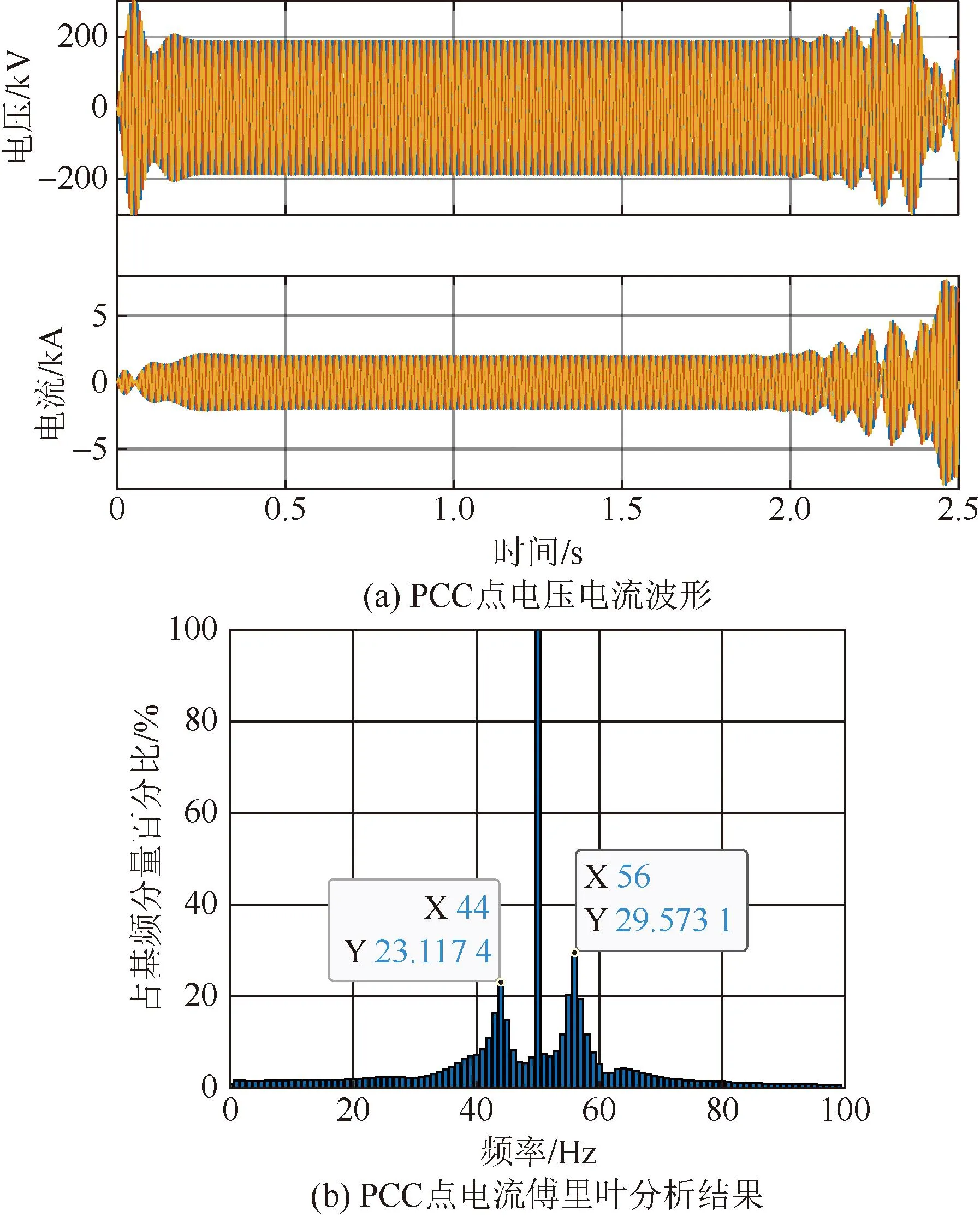
图12 仿真案例1验证结果Fig.12 Verification results of simulation case 1

2)仿真案例2:近工频负序振荡。

仿真中风电场出力逐渐增加,在0.2 s时到达40%的额定功率,互联系统的PCC电压和电流时域仿真波形如图13所示。由前文理论分析可知,互联系统在此工况下,互联系统在59 Hz处的相位裕度为-3.2°,同样为负且接近于0,系统振荡形式与案例1类似。从图13(a)中可以看出,当风电场达到设定出力后,系统在0.5 s左右逐渐出现振荡现象,PCC电流的傅里叶分析结果如图13(b)所示,其振荡频率为59 Hz,时域仿真结果与图6的理论分析一致。

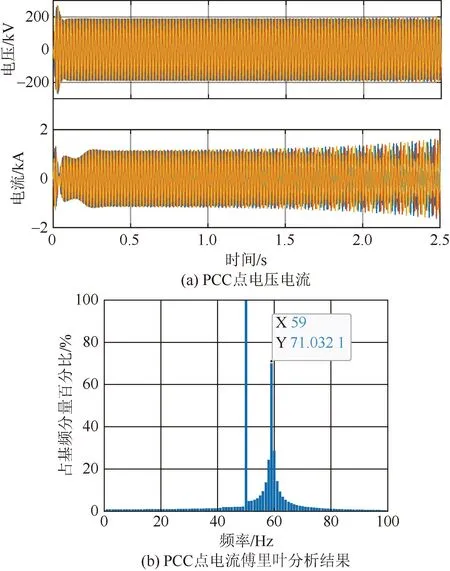
图13 仿真案例2验证结果Fig.13 Verification results of simulation case 2

3.2 近工频正序振荡影响因素分析

基于前文设计的交互案例1,对近工频正序振荡影响因素的理论分析结果进行验证。

仿真案例3:从图10 (b)的理论分析可知,当直驱风电机组网侧变流器的正序电流环比例系数从1 pu增大至1.2 pu时,互联系统由不稳定变为稳定。仿真中,互联系统原始参数与研究案例1一致,在2 s时将直驱风电机组网侧变流器的正序电流环比例系数增大至1.2 pu,互联系统的PCC点电压和电流时域仿真波形如图14所示。从图中可以看出,在调整控制参数前,互联系统产生了44 Hz的近工频正序振荡,而在调整控制参数后,振荡逐渐消失,系统恢复稳定,从而验证了前文理论分析的正确性。

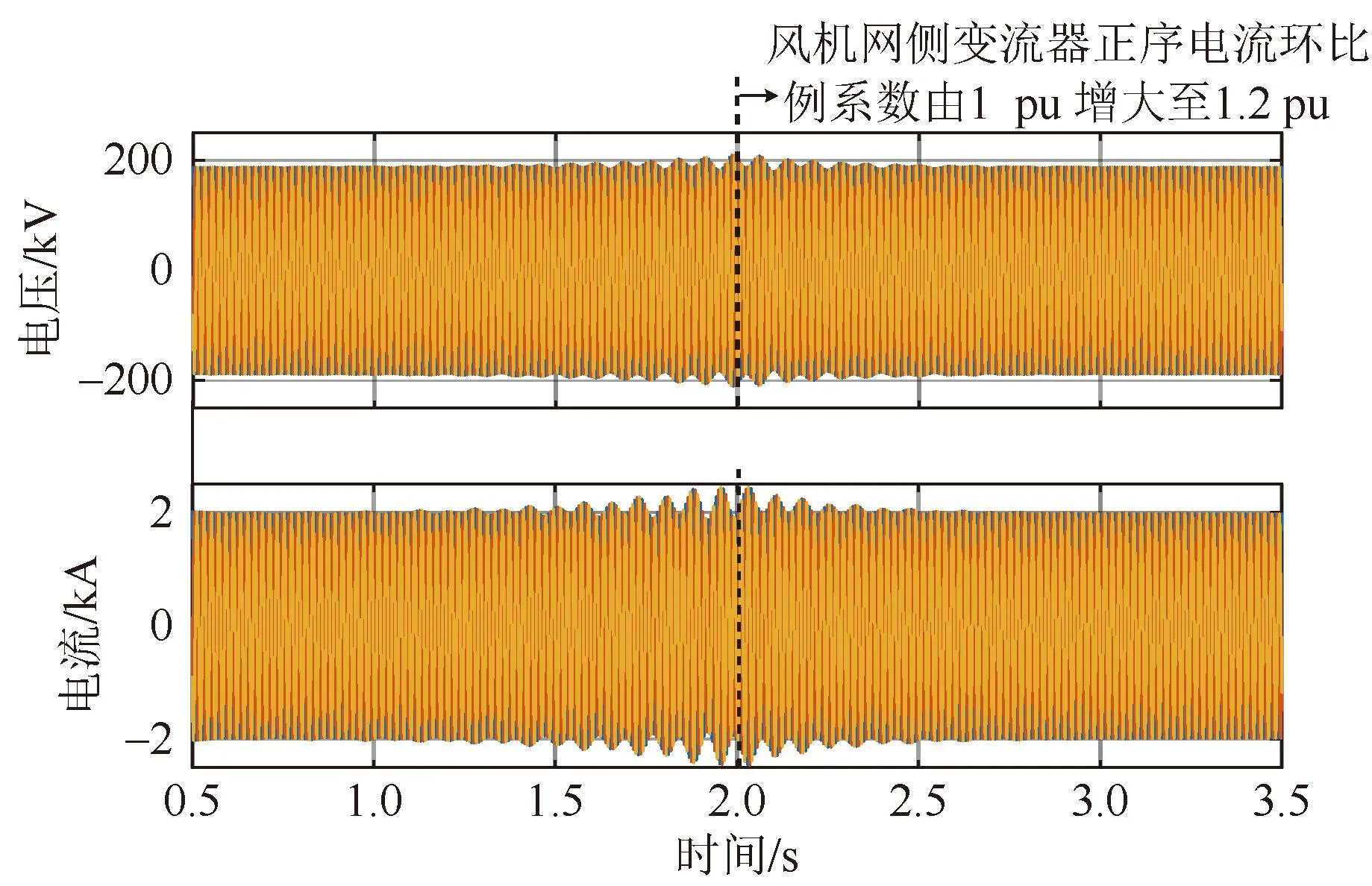
图14 仿真案例3验证结果Fig.14 Verification results of simulation case 3

3.3 近工频负序振荡影响因素分析

基于前文设计的交互案例2,对近工频负序振荡影响因素的理论分析结果进行验证。

仿真案例4:从图11 (b)的理论分析可知,当直驱风电机组网侧变流器的锁相环比例系数从1 pu减小至0.6 pu时,互联系统由不稳定变为稳定。仿真中,互联系统原始参数与研究案例2一致,在2 s时将直驱风电机组网侧变流器的锁相环比例系数减小至0.6 pu,互联系统的PCC点电压和电流时域仿真波形如图15所示。从图中可以看出,在调整控制参数前,互联系统产生了59 Hz的近工频负序振荡,而在调整控制参数后,互联系统振荡逐渐消失,系统恢复稳定,验证了前文理论分析的正确性。

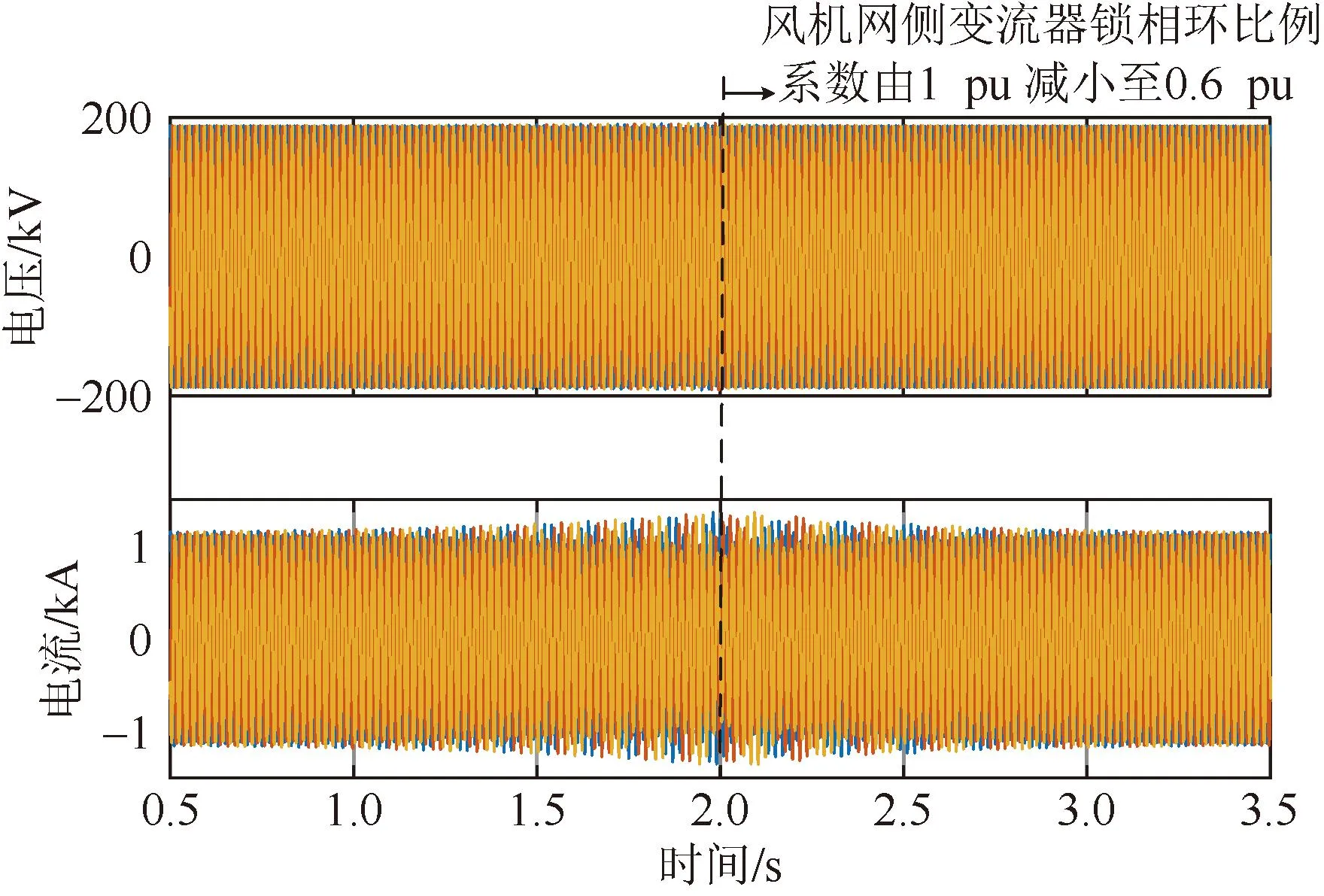
图15 仿真案例4验证结果Fig.15 Verification results of simulation case 4

4 结 论

本文建立了考虑负序控制的直驱风电机组和柔直送端MMC的精细化阻抗模型,揭示了直驱风电场与柔直送端MMC之间产生近工频正序和负序振荡的机理及其关键影响因素。主要研究结论如下:

1)由于正负序控制环节的作用,风电场和柔直送端MMC在近工频段的相位特性呈现互补关系,即一个呈现感性特性、另一个呈现容性特性,且由于风电场在工频附近较强的负电阻特性,当风电场与柔直送端MMC的阻抗幅值在近工频段产生交点时,易诱发近工频振荡风险。

2)近工频正序振荡主要受正序控制参数影响,其中风电机组正序电流环的比例和积分系数、锁相环的比例系数、柔直送端MMC正序电流环的积分系数以及正序交流电压环的积分系数影响较大;近工频负序振荡主要受负序控制参数影响,其中风电机组负序电流环的积分系数和柔直送端MMC负序交流电压环的积分系数影响较大。

3)不同风电场出力下,直驱风电场经柔直送出系统近工频正序或负序振荡的主导影响因素基本保持不变。

附录A

图A1 直驱风电机组的典型拓扑与控制Fig.A1 Typical topology and control of PMSG-based power generation system

图A1中:下标 a、b、c 表示各变量在abc三相静止坐标系下的分量;下标d、q表示在dq旋转坐标系下的分量;下标+、-分别表示正、负序分量;上标s、c分别表示电气坐标系和控制坐标系下的变量;Ht、Hcm分别表示MSC转矩外环、电流内环的比例-积分(PI)控制器传递函数;HDC、HQ、Hcp、Hcn分别表示GSC电压外环、功率外环、正序电流内环、负序电流内环PI控制器传递函数。

图A2中:下标α、β表示各变量在αβ两相静止坐标系下的分量。

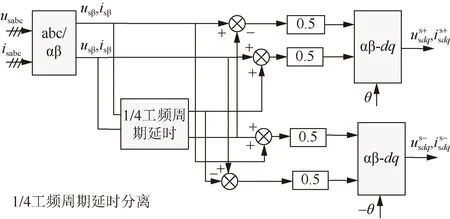
图A2 正负序分离算法结构Fig.A2 Structure of positive and negative sequence separation algorithm

图A3中:s代表拉普拉斯算子;ω0表示基波角频率;HPLL表示锁相环PI控制器传递函数。

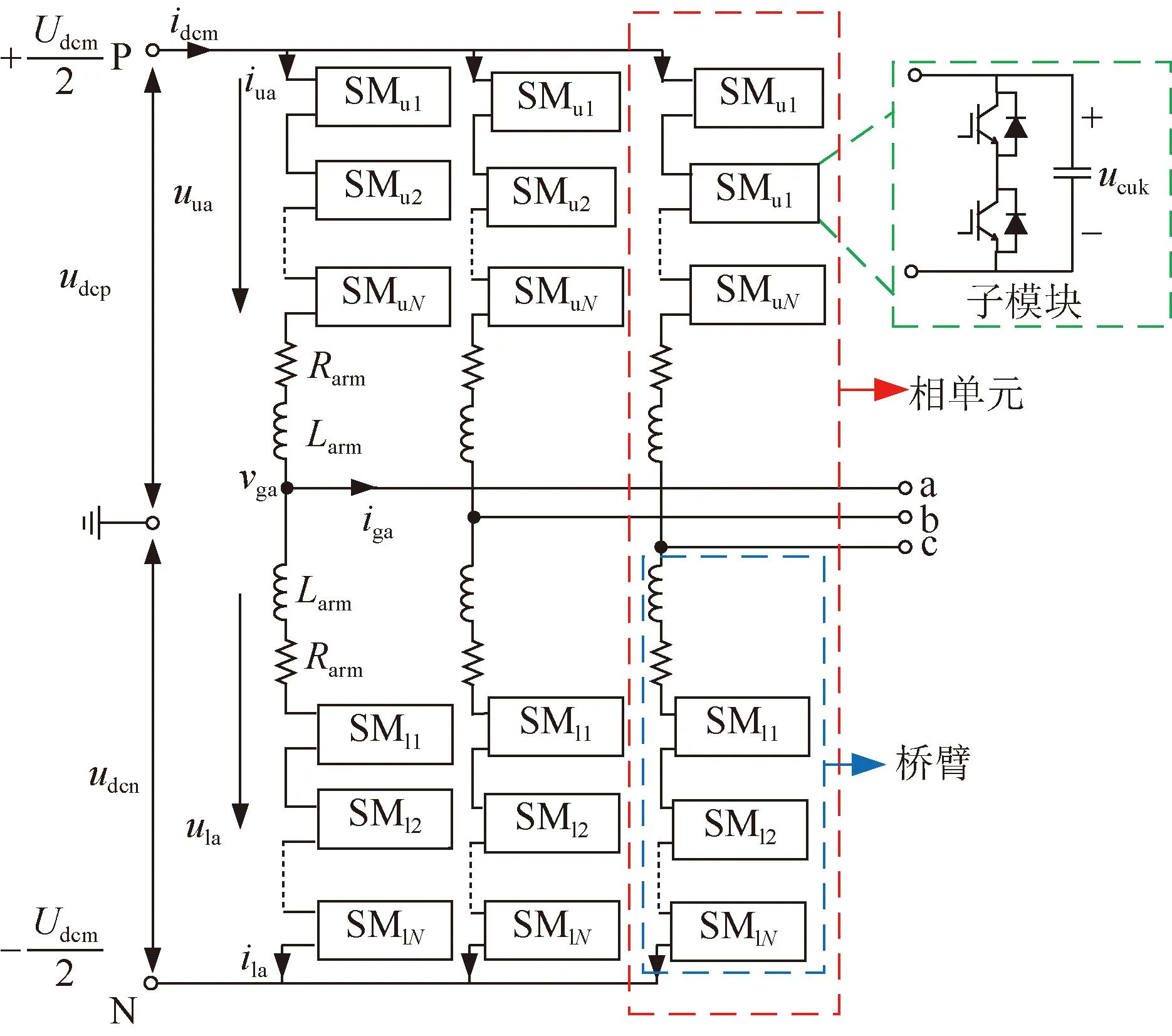
图A4 MMC换流器拓扑Fig.A4 Topology of MMC

图A5中:mux、mlx分别代表上、下桥臂调制函数,ucuxΣ和uclxΣ分别代表上、下桥臂子模块电容电压,iux和iclx分别代表上、下桥臂电流,icom代表桥臂环流,Udcm和ugx分别是直流侧和交流侧电压,igx为MMC交流侧输出电流。

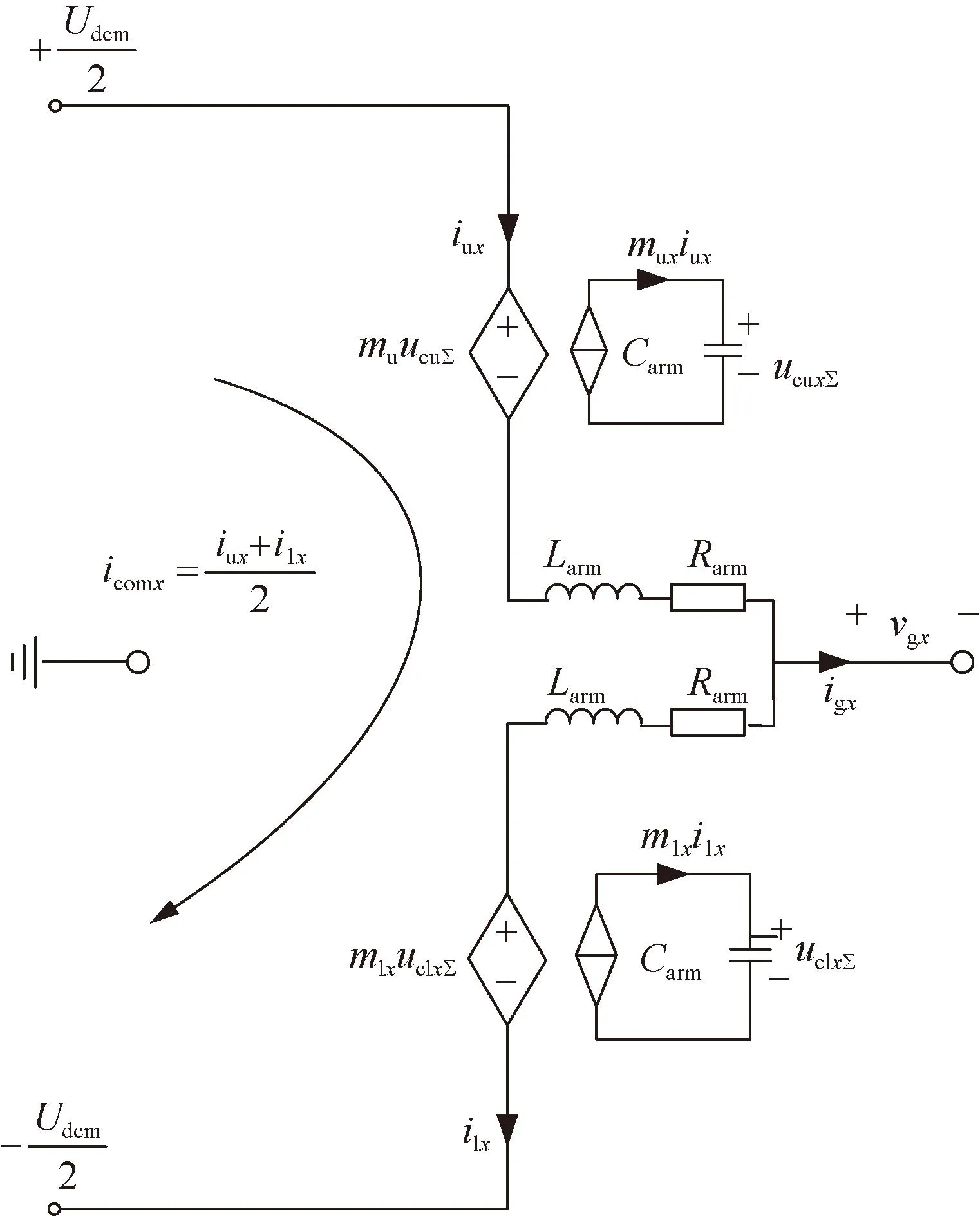
图A5 MMC单相平均等效电路Fig.A5 Equivalent circuit of MMC single-phase leg

附录B

表B1 直驱风电机组参数Table B1 Parameters of the PMSG-based wind turbine system

附录C

正文 1.3节式(7)中的各个系数矩阵为:

(C1)

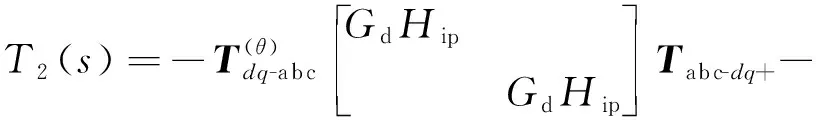
(C2)

(C3)

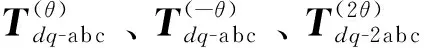
正文 1.3 节式(8)中的各个系数矩阵为:

(C4)

(C5)

(C6)

(C7)

附录D

通过分析各控制环节对直驱风电场和柔直换流站阻抗特性的影响,可以发现:直驱风电场的正序近工频阻抗特性主要受正序电流内环和锁相环的影响,负序近工频阻抗特性主要受负序电流内环的影响;柔直送端MMC换流站的正序近工频阻抗特性主要受正序交流电压外环和正序电流内环的影响,负序近工频阻抗特性主要受负序交流电压外环的影响。由于篇幅限制,此处仅以负序近工频阻抗特性为例,分析以风电场侧负序电流内环和柔直MMC侧负序交流电压外环对风电场和柔直送端MMC负序近工频阻抗特性的影响。

1) 风电场侧负序电流内环的影响。

保持其他参数不变,仅改变直驱风电场负序电流内环带宽分别为100 Hz、200 Hz、300 Hz和400 Hz,直驱风电场在近工频段的负序阻抗特性曲线变化情况如图D1所示。从图中可以看出,负序电流内环对直驱风电场的近工频负序阻抗特性整体影响较大,随着负序电流内环带宽的增加,阻抗的幅值上升。在次同步近工频段,阻抗的感性增强;在超同步近工频段,阻抗的容性增强。

图D1 直驱风电场负序电流内环的影响Fig.D1 Influences of negative sequence current inner loop of PMSG-based wind farm

2) 柔直送端MMC侧负序交流电压外环的影响。

保持其他参数不变,仅改变柔直送端MMC负序交流电压外环带宽分别为10 Hz、20 Hz、30 Hz和40 Hz,柔直送端MMC在近工频段的负序阻抗特性曲线变化情况如图D2所示。从图中可以看出,负序交流电压外环对柔直送端MMC的近工频正序阻抗特性整体影响较大,随着负序交流电压外环带宽的增加,阻抗的幅值下降。在次同步近工频段,阻抗的容性增强;在超同步近工频段,阻抗的感性增强。

图D2 柔直送端MMC负序交流电压外环的影响Fig.D2 Influences of negative sequence AC voltage outer loop of MMC