基于实时生成定值的高比例新能源电网自适应电流保护

张政伟,陈谦,牛应灏,冯源,朱嘉傲

(河海大学能源与电气学院,南京市 211100)

0 引 言

随着新型电力系统的建设,新能源电源的比例不断升高[1-2]。新能源电源通常采用电力电子方式并网,其输出受内部控制策略所决定,且与端电压呈高度非线性关系[3-5]。另外,受一次新能源特性的影响,其二次电源的输出具有明显的随机性和波动性[6]。

电流保护方面,新能源电源的接入使得短路电流与短路距离的相关性大为下降,从而改变了电网的故障特征[7-10],导致传统电流保护配合方案难以适用。电流保护是继电保护系统不可或缺的重要一环,其性能受上述影响较为明显,因此如何改进电流保护动作原理及其整定方法,以满足电流保护的动作性能要求值得深入研究[11-13]。

目前,有些研究利用远方/多点量测信息来实现原理和整定方法的改进。比如,文献[14]基于通信和方向元件检测电流流向以实现故障定位,从而实现保护整定值的实时调整。文献[15]基于逆变型分布式电源的位置对配电网进行分区,进而针对不同区域采用不同的电流保护配置及整定方案。文献[16]计及分布式电源的短路前工况及其脱网特性,实时测量支路电流方向,实现对限时电流速断(II段)保护定值的实时修正。文献[17]根据故障前后线路电流的突变量,实现对负荷自启动的准确识别,但对I段和II段保护性能无提升作用。这类方法对通信的可靠性及信息的准确性要求较高,需额外安装测量设备和通信设备。

另一些研究则利用新能源电源内部运行参数或控制策略的改变实现原理和保护定值的改进。文献[18]基于逆变电源电流-电压控制曲线,研究不同故障类型下新能源接入带来的分支系数影响,进而用于电流保护的整定。文献[19]提出利用逆变器的实时运行参数,进而调整上级线路电流Ⅱ段及Ⅲ段保护的整定值。文献[20]通过逆变器电流-电压控制曲线,求解分布式电源在线路末端设想故障时的输出电流,以用于下游电流保护的自适应整定。文献[21]提出基于变频调制的方式获得线路短路后的虚拟短路电流,但仅适用于微电网。这类研究多基于单台或少量发电单元,通过逆变器内部运行参数与输出特性,以推测本段或相邻线路末端发生设想故障时的新能源虚拟输出电流值,进而对各段线路保护进行预先整定。然而,受新能源分散性、状态多样性与输出非线性等因素的制约,实际场景中新能源运行参数、输出状态均不一且获取较为困难。因此,难以适用于实际故障场景,准确性与适用性有待进一步验证[22]。

为此,本文提出一种仅利用就地信息的实时生成定值式自适应电流保护方法。该方法首先基于建立的等效电源模型,结合故障前后信息,实现故障后新能源和发电机短路输出成分的区分;进一步提出实时生成定值的整定策略,以实时获取适用于当前故障场景的电流保护定值;而当故障场景变化时,各段线路保护则再次基于变化后的故障场景实时整定,实现对故障场景的针对性保护。

该方法主要特点为:1)故障前对等效电源模型参数的持续辨识可应对发电总容量变化和电源构成占比波动的问题;2)基于短路期间的新能源实际故障输出而实时生成定值,可有效规避新能源布置分散性、状态多样性与输出非线性等带来的预先整定方案中所用新能源虚拟输出准确性难以保证的问题。

1 新能源电源控制策略及其接入对电流保护的影响

1.1 新能源电源控制策略

新能源电源通常采用电力电子方式并网,且含有逆变器部件。因此,本文将基于逆变器原理对新能源控制策略进行分析,并在后续基于新能源输出特点进行相应建模工作,以能反映种类多样的新能源的整体外部输出。

若故障点电气距离较远,并网点电压较高,新能源电源常采用恒功率控制策略,更接近发电机的输出特性[23]。若故障点电气距离较近,而并网点电压较低,为避免新能源电源脱网带来更严重的损失,且提供一定的无功功率支撑,逆变器部件需采用低压穿越控制策略。比如,较为通用的新能源电源低压穿越标准要求:当发电单元并网点电压跌落超过10%时,电压每跌落1%,新能源电源至少需要额外提供2%的无功电流以支撑电压,且要求无功响应时间在20 ms以内[24]。

此外,若故障是不对称的,短路点含有的负序分量导致逆变器部件交流侧电流发生畸变,将损坏电力电子器件。逆变器部件需采用负序电流抑制策略,消除负序输出分量,实现新能源电源对称输出。

综上,综合考虑稳态控制策略、抑制负序策略、低压穿越等要求,新能源外部输出电流可表示为[15]:

(1)

式中:idref、iqref分别为新能源电源聚合后等效有功电流指令和无功电流指令;α为故障期间并网点电压正序幅值和故障前正序电压幅值的比值;α1、α2为并网点电压跌落时α变化的界限阈值;Upcc(1)为并网点正序电压;Pref为输出有功参考值;IDG为新能源电源输出电流;数值均为标幺值。

1.2 高比例新能源电源接入对电流保护的影响

不含新能源的传统电网中,短路电流大小与线路长度成反比。而由1.1节分析可知,新能源电源采用的电力电子并网方式,使其具有强自控特征,短路电流与电压跌落程度、控制策略等因素相关,且是强非线性关系。

基于Simulink平台,建立新能源电源模型并搭建模拟电力系统,如图1所示。其中,设定发电机额定电压为10.5 kV;新能源电源采用正常PQ、低压穿越、抑制负序分量等控制策略,并网点电压为10 kV;线路单位长度阻抗为0.22 Ω/km,线路总长为8 km,线路AB长度为1.5 km,线路BC、CD长度各为2 km;负荷侧接有额定功率为5 MV·A、额定功率因数为0.85的负荷。

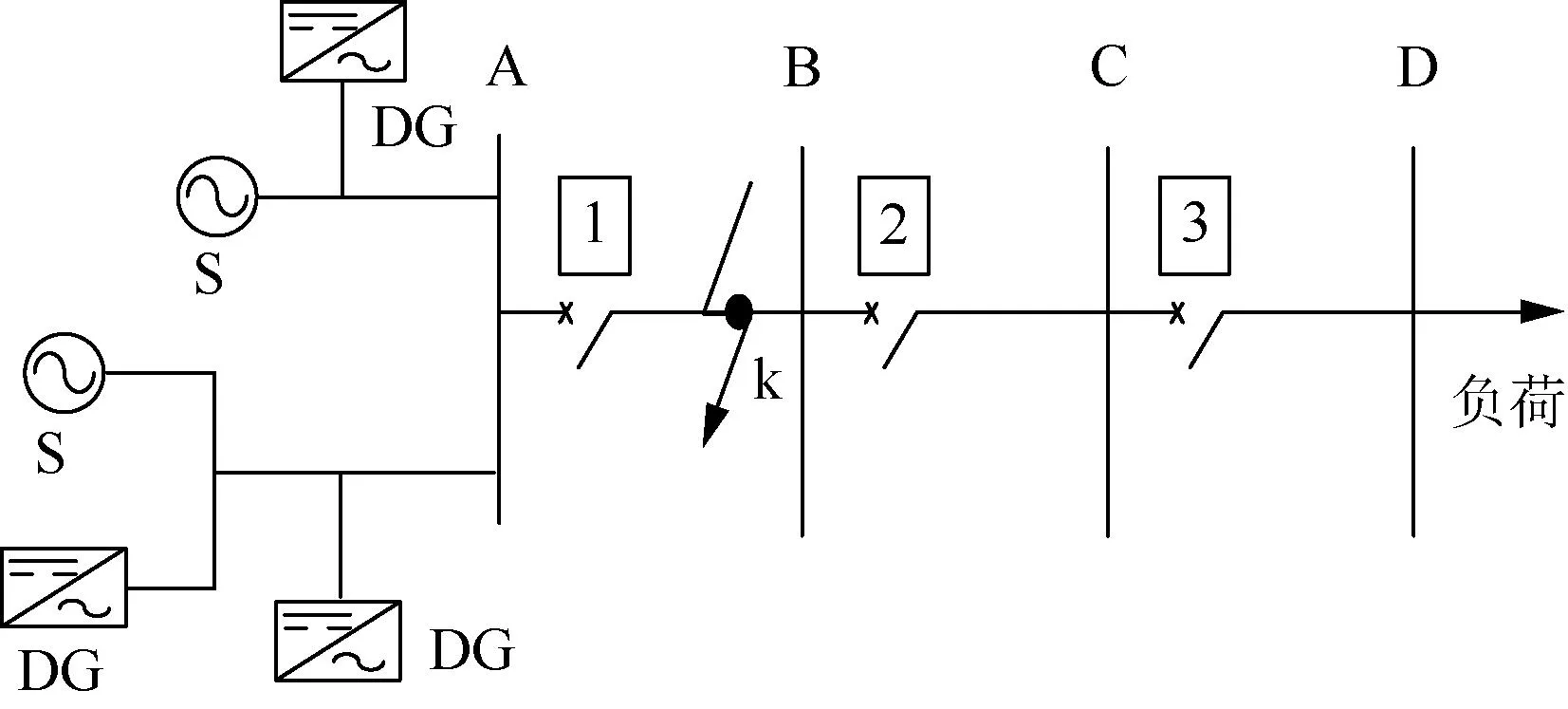
图1 含混合电源的电力系统结构示意Fig.1 Schematic diagram of power system structure with hybrid power supply

进一步,保持电源侧发电总容量不变,针对电源侧新能源电源占比分别为0、5%、20%、40%、60%的5种电力系统模型,设定不同位置故障,获得短路电流与故障位置间的关系,如图2所示(文中图表数值均以标幺值形式表示),重点分析新能源比例升高对电流保护性能的影响。

图2 新能源电源不同占比及不同故障位置下的短路电流Fig.2 Short-circuit current under different proportions of new energy power supply and different fault positions

由图2可知,随着新能源电源占比的升高,一方面短路电流将不断降低,当动作整定值不变时,电流保护面临本段拒动、上游误动的可能。另一方面,短路电流关于故障位置的曲线趋于平缓,即短路距离对短路电流的影响变小;当新能源占比变化而仍采用同一整定值时,保护的有效范围将随着新能源占比升高而不断缩小。

可见,新能源输出非线性造成高比例新能源电网故障特征弱化的同时,其波动性也会导致同一点故障下的短路电流随其占比的波动而波动。因此,针对不同故障场景,自适应地改变各段线路电流保护定值是解决现有电流保护性能下降问题的有效途径。

现有计及新能源的自适应保护整定多基于新能源内部参数、输出特性等,通过推测新能源在各线路末端发生设想故障时的虚拟短路输出,进而实现各段线路保护的预先整定。电源构成不变的前提下,该类研究获取的保护定值对不同位置故障也能适用。但这类研究多基于单台新能源发电单元,而实际场景中新能源运行状态不一样且参数的全面获取较为困难;进而预先整定中各线路末端发生设想故障时所用新能源虚拟输出分量的准确性难以保证,实用性和准确性有待进一步验证。

2 基于实时生成定值的高比例新能源电网电流保护方法

由第1节分析可知,电流保护预先整定方案中存在所用新能源虚拟输出分量难以准确推测或计算的问题。

而故障期间的新能源实际短路输出分量确定,进而基于该值生成的保护定值可满足该实际故障场景下的保护需求。故障场景变化时,新能源实际故障输出分量的改变可能导致原有保护定值难以继续适用,但基于变化后的新能源实际故障输出再次实时整定即可。

综上,本文提出了一种利用就地信息的自适应电流保护改进方法,该方法基于实际故障场景、计及故障期间新能源实际输出而实时生成保护定值。原理如图3所示,具体包括如下:

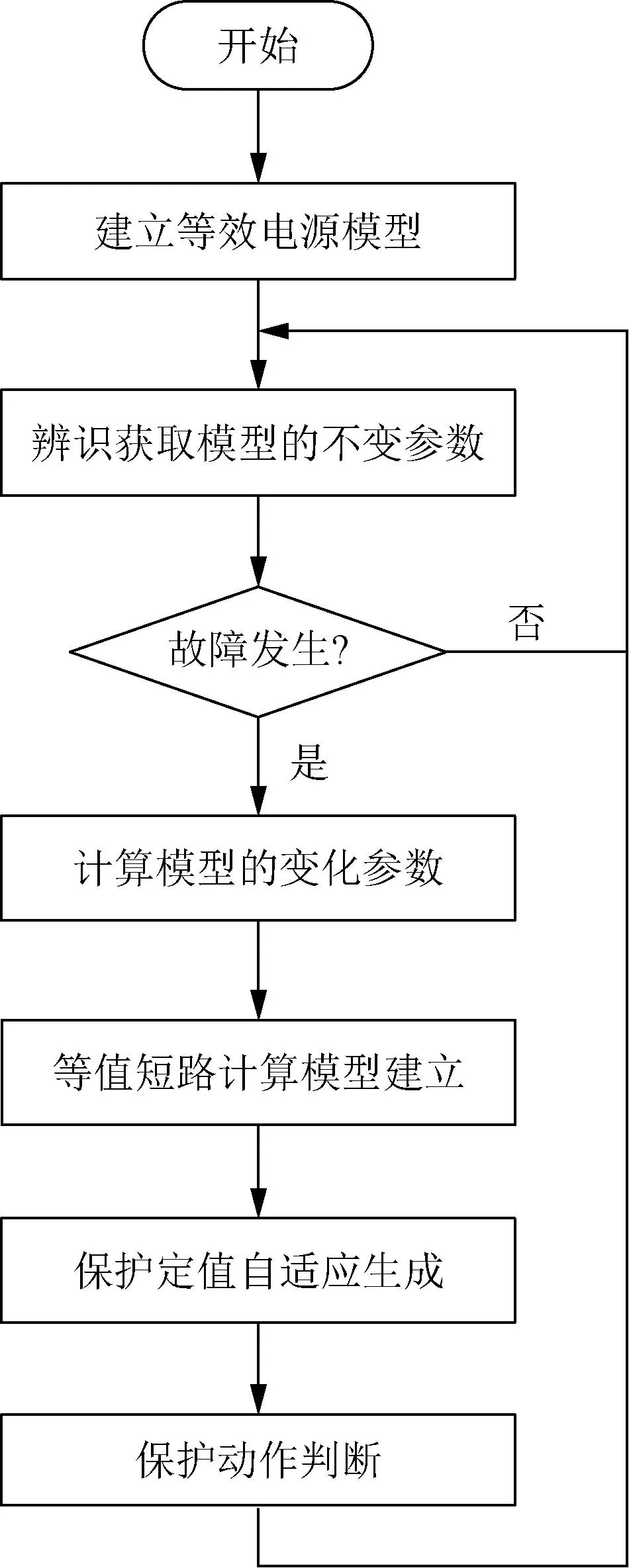
图3 基于实时生成定值的自适应电流保护方法原理Fig.3 Principle of real-time generated protection settings based adaptive current protection

1)计及新能源和发电机的关键机理和外部输出特性,建立能区分2种电源成分不同外部输出的等效电源模型;故障前,利用负荷投切带来的小扰动信号持续辨识模型的不变参数。

2)故障期间,结合就地信息获取模型的可变参数--新能源实际故障输出电流。

3)基于实际故障场景、计及故障期间新能源实际输出,对分段式电流保护实时生成定值。

4)结合测量值与整定值进行动作判断;故障场景变化后,各段线路保护再次基于变化后的故障场景实时生成保护定值,实现对故障场景的针对性保护。

2.1 等效电源模型

实际故障场景中,新能源的短路输出与并网点和短路点间的电气距离有关,其分散性导致新能源输出状态不一,进一步与输出非线性等耦合使得单台或少量的发电单元难以模拟实际故障场景。

为此,本文综合计及新能源和发电机的关键机理和输出特性,建立一种能区分2种电源成分不同外部输出的等效电源模型,以消除新能源状态多样性、布置分散性、输出非线性等因素对电流保护的影响。

由1.1节分析可知,电网正常运行状态下,各节点电压相对处于额定运行工况,采用恒功率控制方式并网的新能源输出电流相对恒定、波动较小。电网故障期间,与故障点电气距离较远的新能源并网点电压依旧接近额定电压,输出电流基本不变。而少数靠近短路点的新能源电源因电气距离较短而处于低压穿越状态,但在负序抑制策略下,短暂的过渡过程后,很快保持稳定且仍对称输出。因此,单个新能源输出可用与并网点电压相关的电流源表示,而电源侧新能源整体外部输出可用单个输出可变的电流源等效表示[25-26]。

另外,参照现有发电机建模研究,发电机可视为内部具有相同的恒定内电势,因此电源侧发电机可等值为电压源串联阻抗的形式。

综上,以短路点为基点、电源侧为观测方向,建立电源侧等效模型,如图4所示。其中,故障前后模型的不变参数包括:发电机内电势E和内阻抗ZS;可变参数为新能源输出电流IDG,故障前后分别用IDG0和IDG1表示。

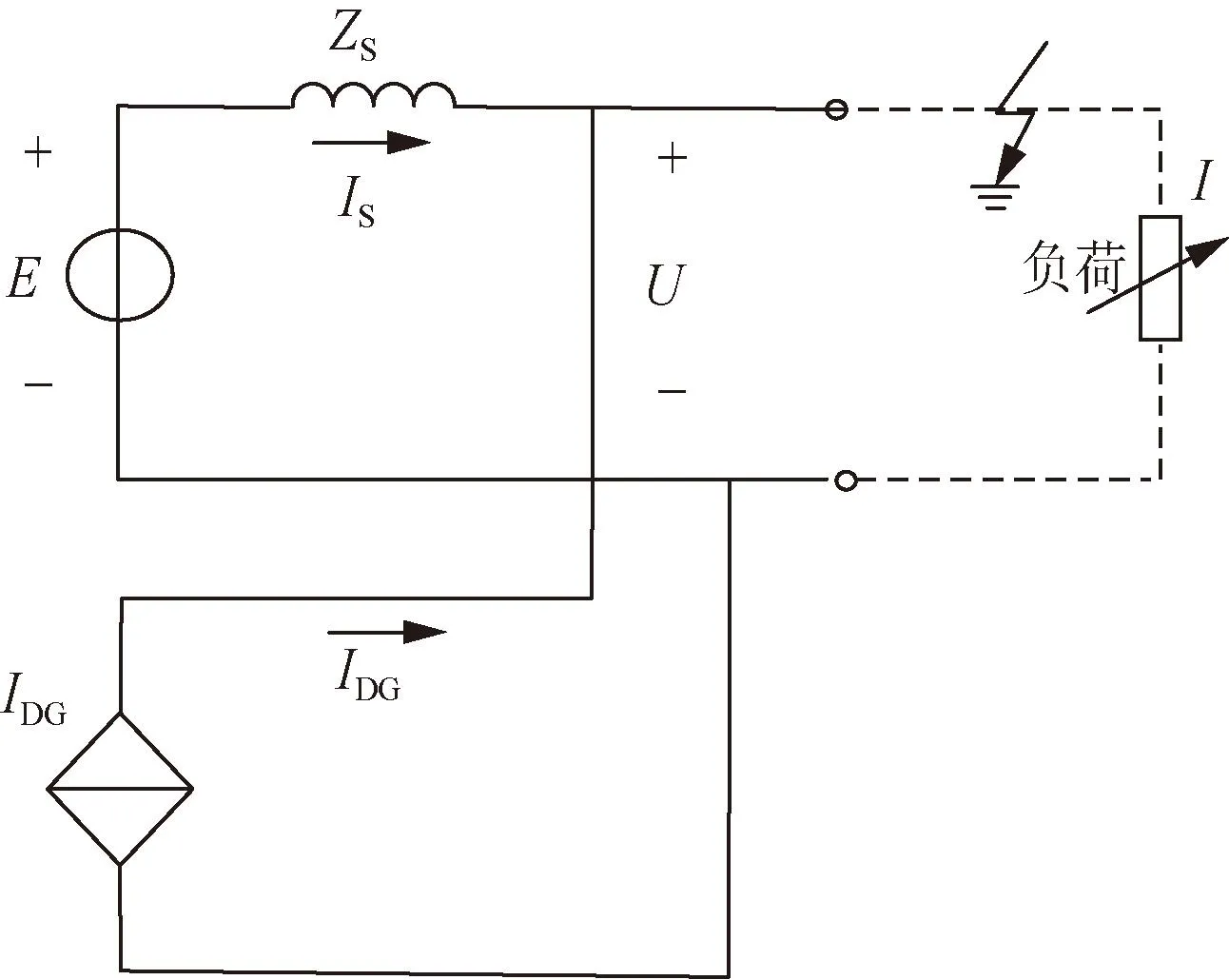
图4 等效电源模型Fig.4 Equivalent source model

此外,当前及未来可预见一段时间内新能源电源仍以跟网型为主且其对电流保护影响较大,因此本文所述新能源电源均为跟网型新能源电源(电流源特性),而未来并网的构网型新能源电源因其电压源特性则可归入传统发电机建立等效电源模型[27-28]。

2.2 等效电源模型参数辨识

接下来,为应对新能源波动性和随机性带来的等效电源模型参数变化问题,通过负荷侧投切带来的小扰动信号,故障前在周波级尺度下采用持续辨识策略以获取图4等效电源模型的不变参数--发电机内电势E和内阻抗ZS,同时还可获得新能源电源的故障前输出电流IDG0。

为兼顾辨识精度和速度,本文采用重点参数辨识、非重点参数使用运行典型值的辨识策略[29-30]。其中,需要辨识的参数包括发电机内阻抗ZS、故障前新能源电源输出电流IDG0,而内电势E可采用运行经验值,本文后续取1.03 pu[31]。

设发电机内阻抗ZS和故障前新能源电源输出电流IDG0待定,线路流经电流计算值可表示为(E-U)/ZS+IDG0,线路电流实测值为I,以两者间差值的绝对值最小,建立目标函数及相应约束:

(2)

式中:U、I分别为故障前保护安装处实测电压值和电流值;IDG0,min、IDG0,max分别为故障前新能源波动下可能出现的电流最小值、最大值;ZS,min、ZS,max分别为新能源波动下发电机内阻抗的最小值、最大值。

可在周波级尺度下求解上述最优问题,得出模型参数。通常可用内点法、信赖域反射算法、序列二次规划算法(sequence quadratic program,SQP)、活动集算法等求解该问题。而内点法收敛性较好、计算速度较快,相对较为成熟,且得到的解一定是可行解,因此本文采用内点法。

内点法原理如下:

设定最优化问题的目标函数为:

(3)

式中:f(X)为目标函数;gu(X)为约束函数;m为约束函数的个数。本文共2个约束条件,故m为2。

构造惩罚函数为:

(4)

式中:r(k)为惩罚因子,为递减的正数序列,通常取r(k)=1,0.1,0.01,0.001,…。

迭代步骤如图5所示。

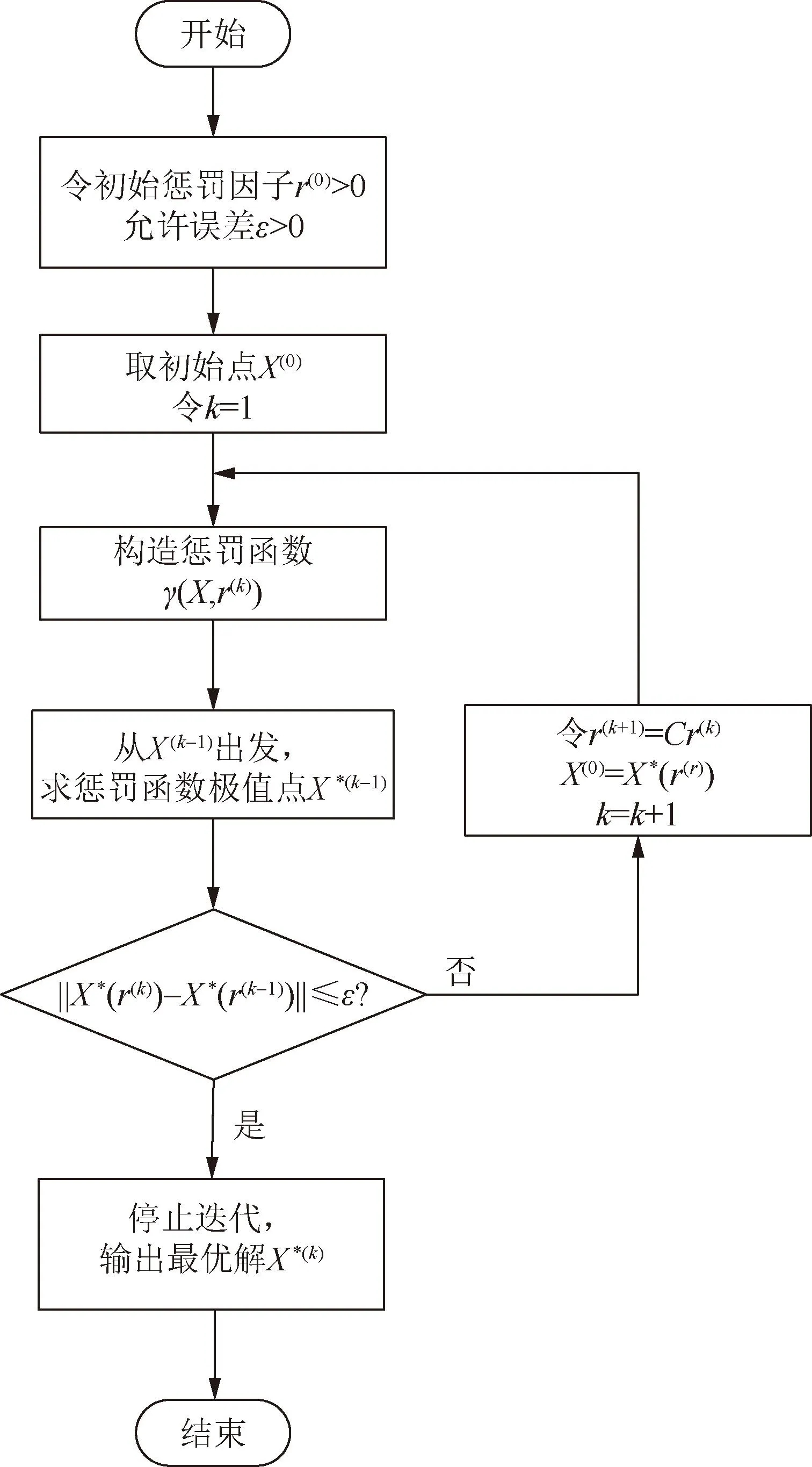
图5 内点法迭代流程Fig.5 Iterative process of interior point method

经过上述内点法迭代求解,可得等效电源模型的不变参数--发电机内阻抗ZS,同时还可获得故障前新能源电源输出电流IDG0。

2.3 基于实时生成定值的自适应电流保护整定方法

根据2.2节获得的等效电源模型不变参数,故障期间结合就地测量信息获取等效电源模型的变化参数--故障期间新能源输出电流IDG1。进一步,基于实际故障场景和故障期间新能源实际输出实时生成保护定值。

首先,利用2.2节获取的电源侧等效模型不变参数ZS和电力线路故障期间保护安装处就地测量信息,计算短路电流中发电机输出部分:

(5)

式中:IS1为故障期间发电机输出电流值;Uk为故障期间保护安装处实测电压值。

进一步,计算故障期间新能源实际输出电流IDG1:

IDG1=Ik-IS1

(6)

式中:IDG1为故障期间新能源电源实际输出电流值;Ik为故障期间保护安装处实测电流值。

针对该实际故障场景,建立图1的等值短路计算模型,如图6所示。

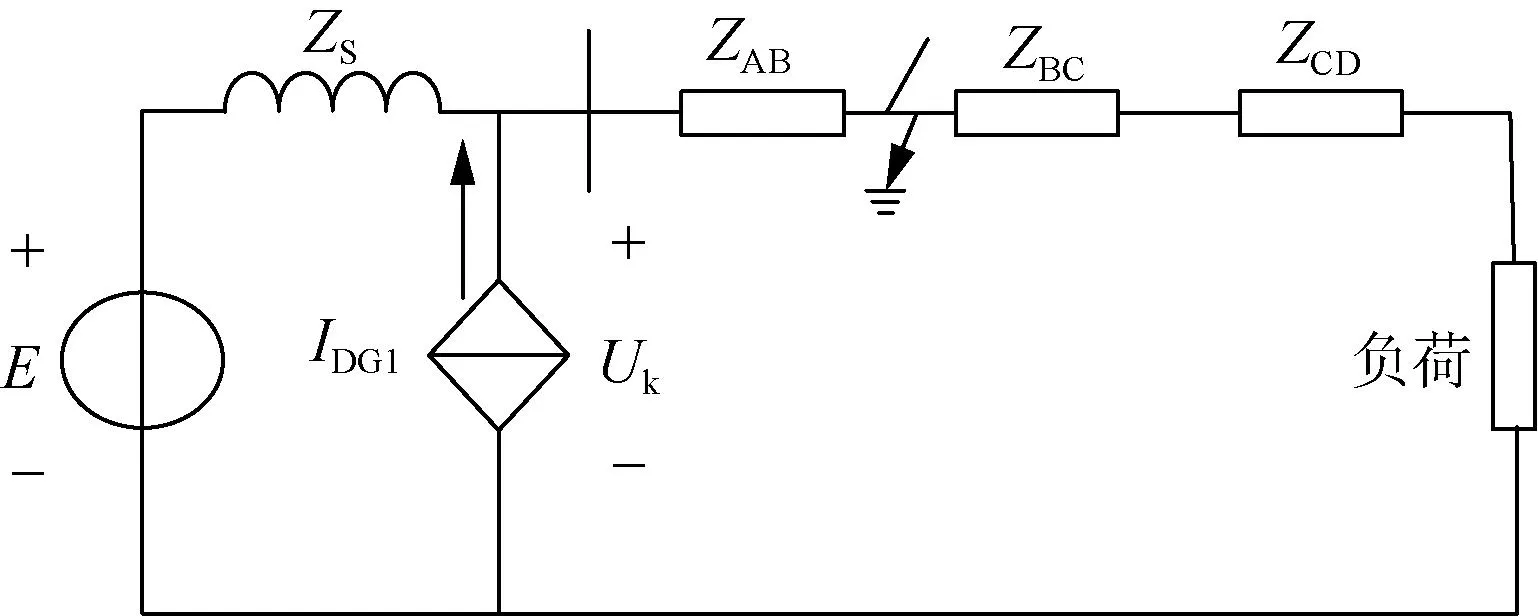
图6 等值短路计算模型Fig.6 Equivalent short-circuit calculation model

进一步,基于该实际故障场景和故障期间新能源实际输出而实时生成保护定值。

以图1的保护1为例,其Ⅰ段、Ⅱ段、Ⅲ段保护动作定值分别为:

(7)

(8)

(9)

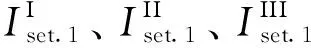
定值实时生成中,使用新能源实际故障输出代替预先整定方案中所用各线路末端发生设想故障时的新能源虚拟输出,以实时生成适用于该场景的定值。故障场景改变(不同新能源占比、不同故障位置)时,新能源实际故障输出也相应改变,进而基于变化后的新能源实际故障输出再次实时生成定值,实现对故障场景的针对性保护,如图3所示。

3 算例对比与分析

在如图1所示模拟电力系统中,以新能源电源占比为0、5%、20%、40%、60%代表其无、低、中、高、极高5种场景。利用常规负荷投切带来的小扰动信号(仿真实验中负荷投切5%左右,造成保护安装点电压波动2%左右)对电源侧等效模型的参数进行辨识。获取模型参数如表1所示。

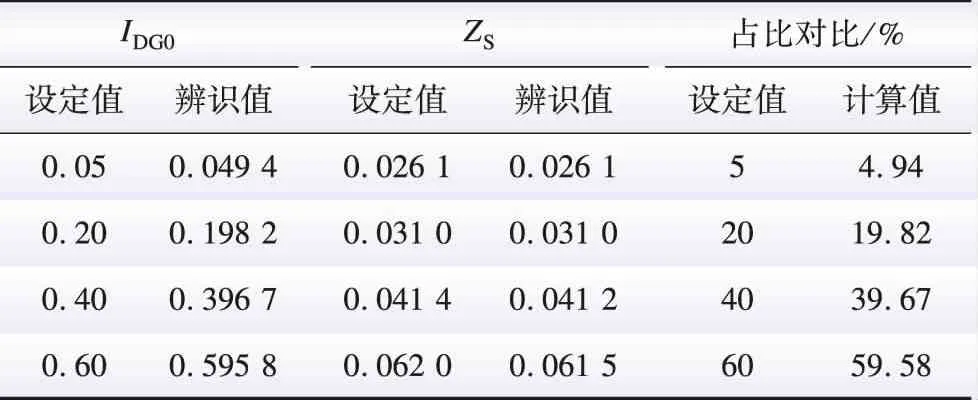
表1 等效电源模型参数Table 1 Parameters of equivalent source model

由表1可见,利用负荷侧投切或冲击性负荷带来的小扰动信号,能够辨识获取电源侧模型的关键参数。

传统电流保护整定过程中不计及新能源电源接入带来的影响,即其整定过程中认为电源侧仅含有发电机,可得相应的动作整定值,如表2所示,以作为对照。

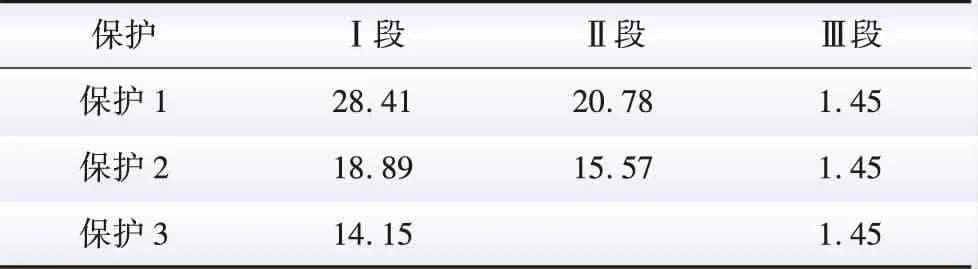
表2 传统电流保护动作整定值Table 2 Preset values of traditional current protection

下面就保护的Ⅰ段和Ⅱ段性能进行对比分析。

3.1 保护Ⅰ段定值对故障的反应

1)三相短路故障。

在距各线路首端20%处设定三相短路故障,获取线路短路电流及相应Ⅰ段保护动作整定值,如表3所示。

表3 线路首端三相故障场景下Ⅰ段保护动作整定值Table 3 Preset values of protection section I under three-phase fault scenario at the head of the line

接下来,对比分析传统电流保护方法和基于实时生成定值的自适应电流保护方法能否反映该处故障,如表4所示。

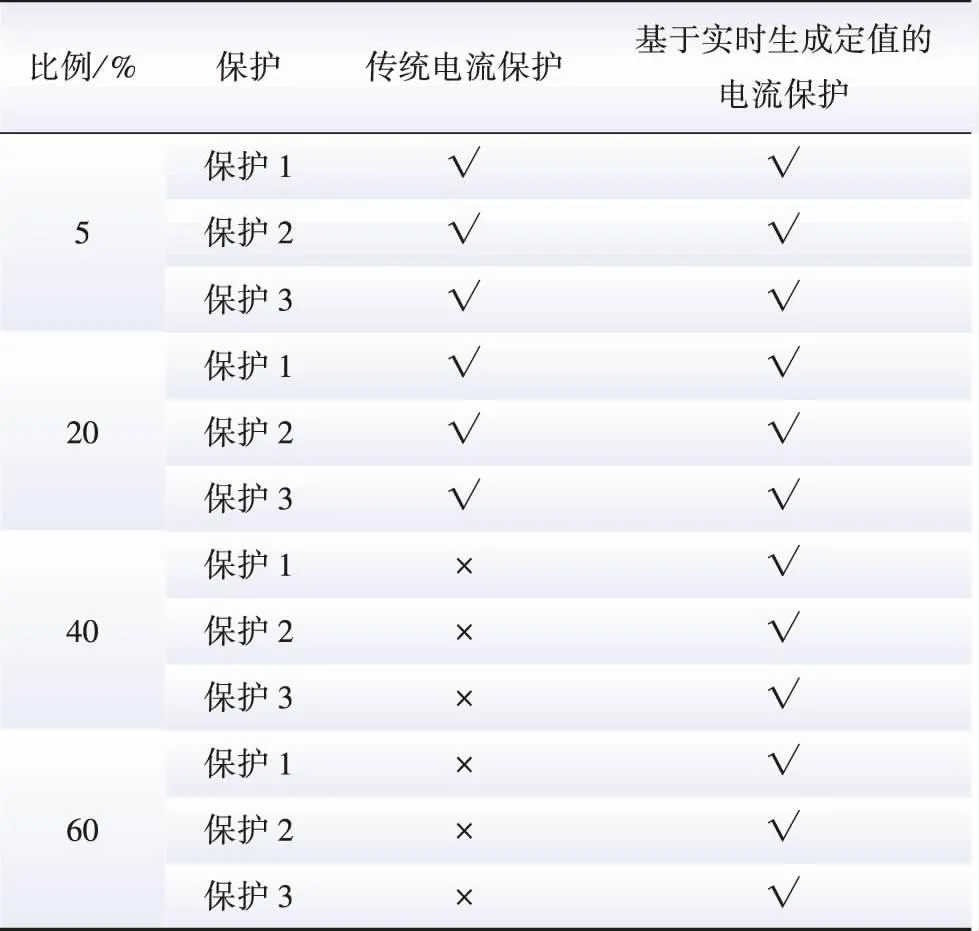
表4 保护Ⅰ段对线路首端三相故障反应情况Table 4 Response of protection section I to three-phase fault at the head of the line

2)两相短路故障。

在距各线路首端20%处设定两相短路故障,获取线路短路电流及相应Ⅰ段保护动作整定值,见表5。

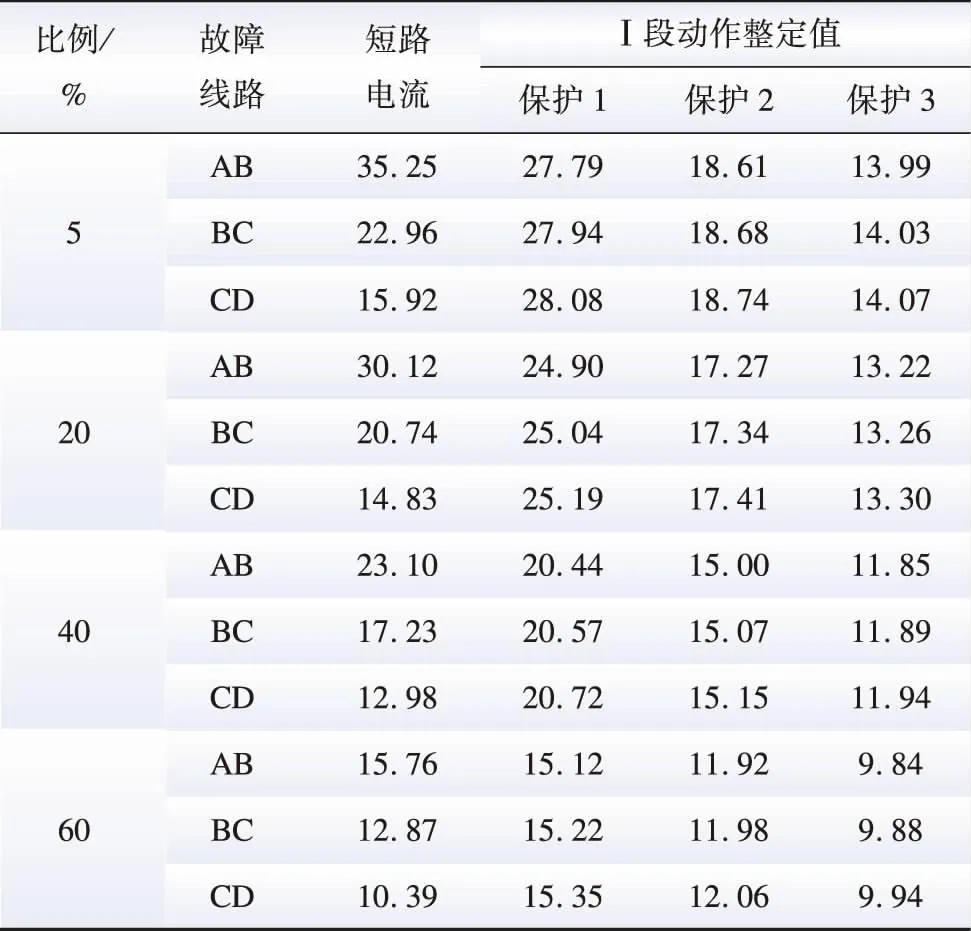
表5 线路首端两相故障场景下Ⅰ段保护动作整定值Table 5 Preset values of protection section I under two-phase fault scenario at the head of the line

接下来,对比分析传统电流保护方法和基于实时生成定值的自适应电流保护方法能否反映该处故障,见表6。

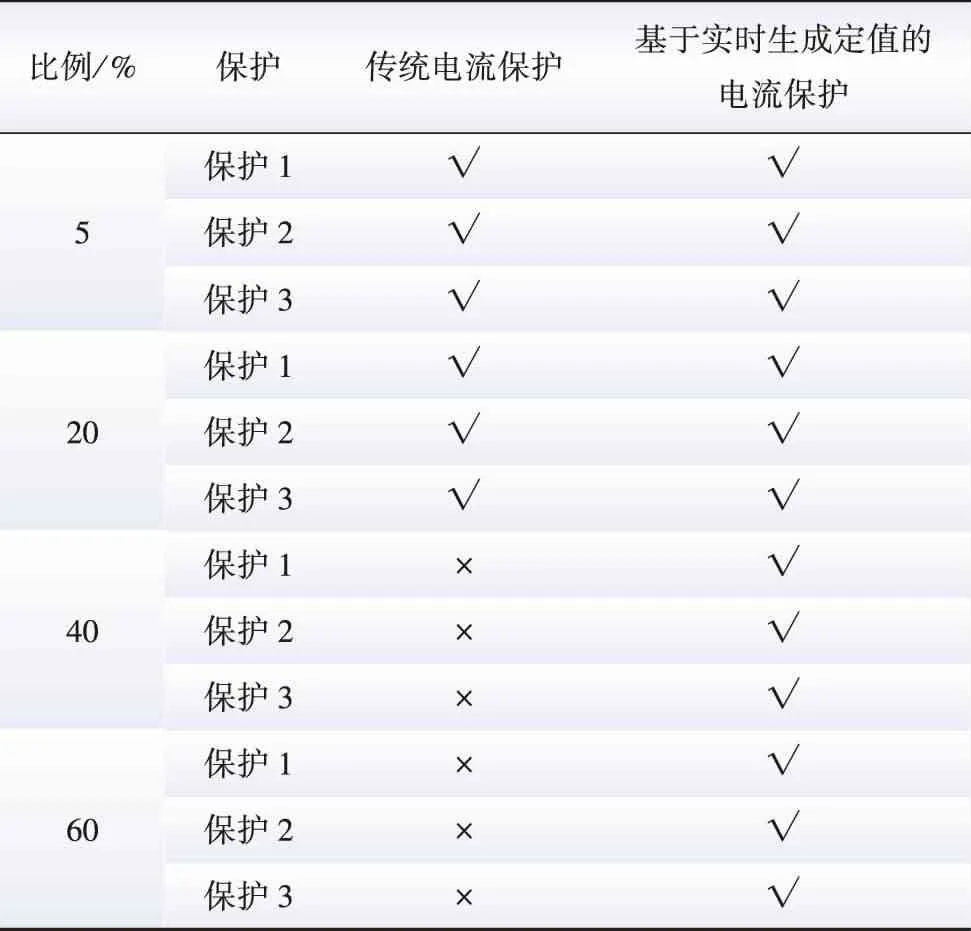
表6 保护Ⅰ段对线路首端两相故障反应情况Table 6 Response of protection section I to two-phase fault at the head of the line

由上述对比分析可见,随着新能源比例的提高,传统电流Ⅰ段保护难以准确反映区间(线路全长20%)内故障,而本文提出的基于实时生成定值的自适应电流保护方法能准确反映区间(线路全长20%)内的故障。

3.2 保护Ⅱ段定值对故障的反应

1)三相短路故障。

在各线路末端处设定三相短路故障,获取线路短路电流及相应Ⅱ段保护动作整定值,见表7。

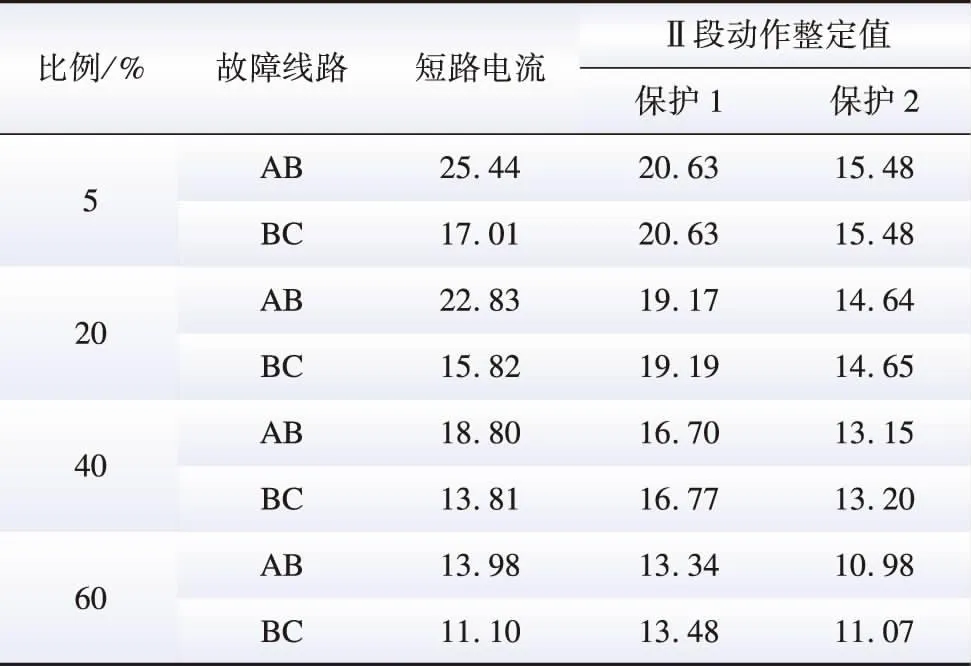
表7 线路末端三相故障下Ⅱ段保护动作整定值Table 7 Preset values of protection section Ⅱ under three-phase fault scenario at the end of the line

接下来,对比分析传统电流保护方法和基于实时生成定值的自适应电流保护方法能否反映该处故障,见表8。

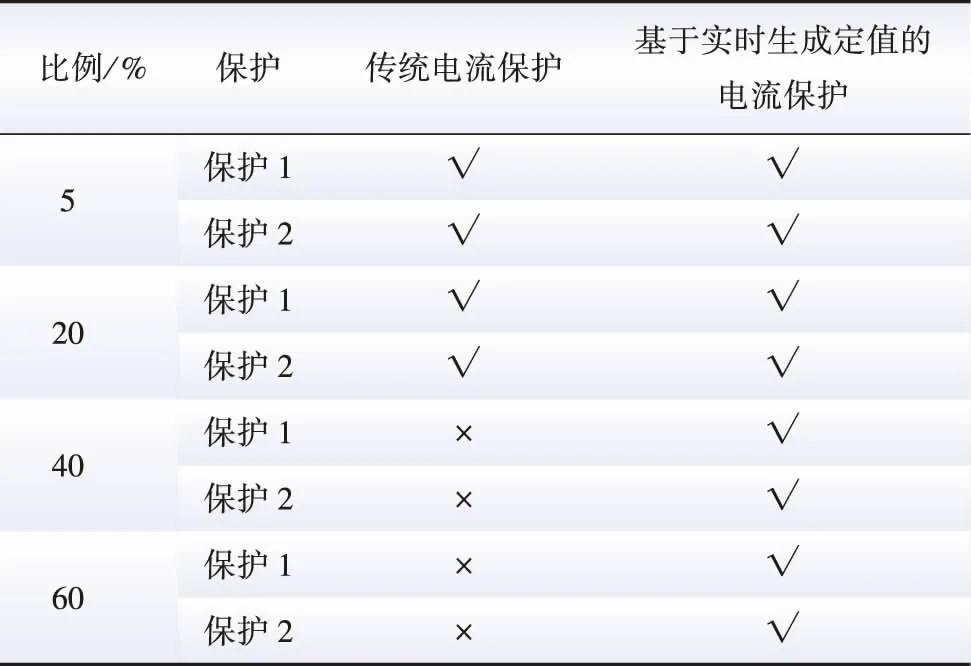
表8 保护Ⅱ段对线路末端三相故障反应情况Table 8 Response of protection section Ⅱ to three-phase fault at the end of the line

2)两相短路故障。

在各线路末端处设定两相短路故障,获取线路短路电流及相应Ⅱ段保护动作整定值,见表9。

表9 线路末端两相故障下Ⅱ段保护动作整定值Table 9 Preset values of protection section Ⅱ under two-phase fault scenario at the end of the line

接下来,对比分析传统电流保护方法和基于实时生成定值的自适应电流保护方法能否反映该处故障,见表10。

表10 保护Ⅱ段对线路末端两相故障反应情况Table 10 Response of protection section Ⅱ to two-phase fault at the end of the line

由上述对比分析可见,随着新能源比例的提高,传统电流Ⅱ段保护难以准确反映区间(线路全长)内故障,而本文提出的基于实时生成定值的自适应电流保护方法能准确反映区间(线路全长)内故障。

3.3 保护II段灵敏性对比与分析

以两相短路下各Ⅱ段保护的灵敏性为例,对比分析传统电流保护和基于实时生成定值的自适应电流保护方法的性能,见表11。

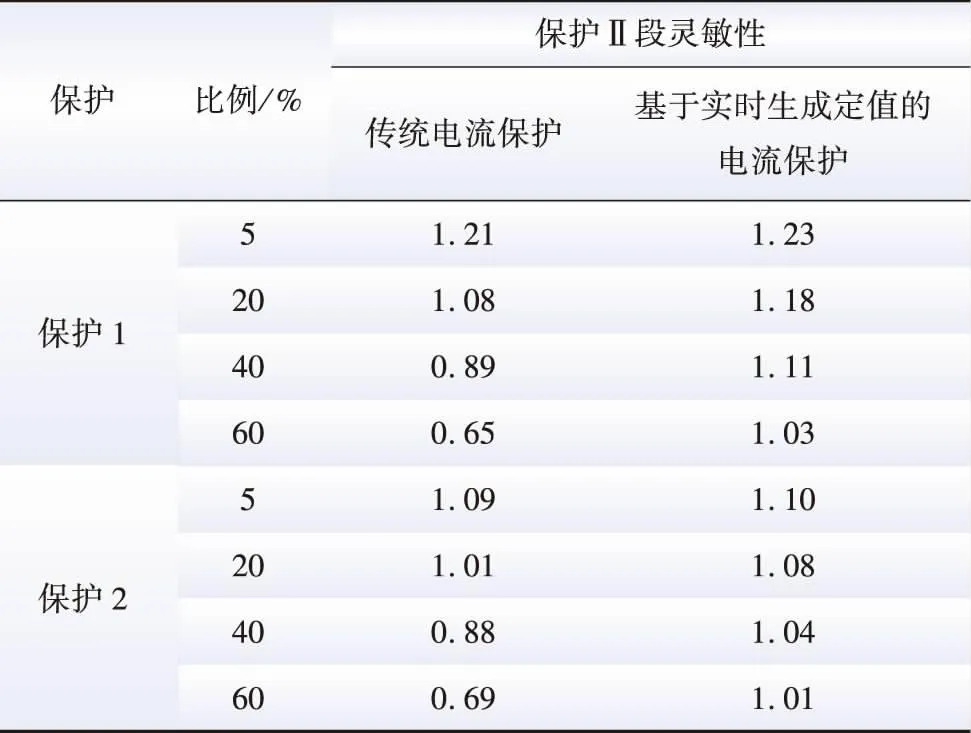
表11 保护II段灵敏性性能对比Table 11 Comparison in sensitivity of protection section II

随着新能源电源比例的升高,传统电流保护的Ⅱ段灵敏性不断下降,将达不到相关技术标准要求;而本文提出的基于实时生成定值的自适应电流保护方法能保持较高的灵敏性,且新能源比例越高,该方法的灵敏性优势越明显。

4 结 论

未来电网中含有高比例新能源电源,因其波动性、非线性等因素,造成短路后故障电流受新能源电源的影响增大,基于传统短路电流计算分析的电流保护难以适用。本文提出了一种基于实时生成定值的自适应电流保护方法,该方法能基于故障期间的新能源实际故障输出而自适应地实时改变保护动作定值,确保各段保护均能反映区内故障,且大幅提高保护的灵敏性。通过算例对比与分析,验证了该方法的准确性和适用性。

该方法的实现可依托现有硬件平台,只需引入保护安装点的电压信息,具备较好的技术延展性;采用保护安装点侦测的方法,可计及电源侧量大类杂的新能源电源总体特性,具有较好的普适性;采用在线持续跟踪的策略,适用于新能源输出占比不断变化的不同故障场景,具有较好的自适应性。

后续仍需进一步研究:1)计及相邻线路负荷的影响对该方法进行改进;2)该方法原理较常规电流保护复杂,后续需对其可靠性进行深入研究;3)本文暂未计及接于线路中间或末端的新能源,后续需进一步研究其对所提保护方法的影响,并结合综合负荷建模研究等对所提保护方法性能进一步优化。