质子交换膜电解制氢系统建模研究综述

宋洁,郜捷,梁丹曦,李根蒂,邓占锋,徐桂芝,章雷其,谢长君,徐超

(1.华北电力大学能源动力与机械工程学院,北京市 102206;2.先进输电技术国家重点实验室(国网智能电网研究院有限公司),北京市 102209;3.国网浙江省电力有限公司电力科学研究院,杭州市 310014;4.武汉理工大学人工智能与新能源汽车现代产业学院,武汉市 430010)

0 引 言

随着全球气候变暖问题日益严峻,氢能作为一种清洁高效、安全可持续的二次能源,在能源转型中发挥着越来越重要的作用。氢能作为一种二次能源,在能源、化工、交通、冶金等领域具有广泛的应用前景,可以推动能源清洁高效利用,实现大规模深度脱碳[1-2]。质子交换膜(proton exchange membrane,PEM)电解制氢系统是由PEM电解槽和其他辅助设备构成,可以将波动的可再生电力转化为易存储的氢气,既可以实现电力系统的平衡[3],也可以替代高碳氢源和基础原料,减少碳排放[4]。

与传统的碱性电解制氢相比,PEM电解制氢具有占地面积小、电流密度高、响应速度快等特点,能够在更高的电流密度、温度和压力下工作,具有更强的波动适应性[5],是可再生能源制氢的重要技术路线,逐步成为研究与应用的热点技术。然而,PEM电解制氢技术的发展还面临着一些挑战,如电解制氢的高成本、低稳定性、难以适应可再生能源的波动性等[6]。通过模型的建立,可以明晰其内部机理与过程规律,深入分析各类型参量对系统性能的影响规律与影响权重,解析各类型参量的动态变化规律,掌握系统电、气、热等多物理场多时间尺度的动态响应特性,如图1所示。并通过性能及动态行为分析,实现电解制氢系统的优化设计、参数匹配、过程控制及性能预测等目的。

PEM电解制氢系统模型构建涉及电化学、传质、传热等多种复杂非线性过程,及多部件耦合,其建模方法复杂[7]。近年来,国外学者开展了PEM电解制氢系统建模研究,取得了丰硕成果,而国内目前尚处于起步阶段。D.S. Falcão等人[8]综述了PEM电解槽的建模方法,包括基本原理、极化损耗、动态行为、两相流、热效应和经验模型,旨在为该领域的初学者提供指南。P Olivier等人[9]综述了低温电解系统建模工作,包括碱性和PEM技术,通过分类和深入分析不同类型的模型,指出了该领域的优势、不足和未来研究方向。A Majumdar等人[10]综述了PEM电解槽的控制导向模型,讨论了电化学、热质传输和等效电路模型,探讨了不同的控制器设计和控制技术,以提高PEM电解槽的性能和效率。李建林等人[7]综述了PEM电解槽建模的进展,通过层级分析方法,包括机理建模、半经验建模、经验建模和数据驱动建模,为PEM电解槽材料、结构和特性分析等建模研究提供了参考和展望。吴启亮等人[11]综述了可再生能源制氢建模技术,强调了多元仿真模型的重要性,以促进可再生能源与氢储能的耦合系统设计与控制,为实现零碳供能和绿色用能的能源结构转型提供了理论基础。

现有PEM电解综述论文多集中于电解槽本体建模,系统级的研究综述基本处于空白。本文相比已有综述论文的创新点在于本文针对PEM电解制氢系统建模方法进行全面综述,不仅对PEM电解槽模型进行了详细的介绍和比较,还对PEM电解制氢系统的辅机模型进行了全面的梳理和分析,包括水泵、压缩机、冷却器等部件,填补了该领域综述研究的空白。本文从PEM制氢系统工作原理出发,综述PEM电解制氢系统建模方法,从水、热、电、气四个方面深入分析PEM电解制氢系统建模现状,总结已有成果,并提出后期可持续研究与改进的方向。此外本文不仅对PEM电解制氢系统的静态特性进行了阐述,还对PEM电解制氢系统的动态特性进行了重点关注,模型能够用于研究可再生能源输入波动对系统响应和稳定性的影响,为系统控制和优化提供了理论依据。

1 PEM电解制氢原理与系统概述

PEM电解水制氢技术是基于离子交换技术的高效电解技术。PEM电解槽示意图如图2所示,主要由质子交换膜和阴、阳两个电极构成。质子交换膜与阳极、阴极紧密接触,构成了一个类似于三明治结构的电池。

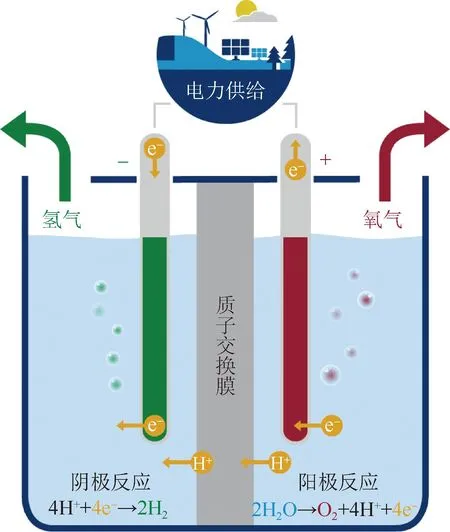
图2 PEM电解槽示意图Fig.2 Schematic of PEM electrolysis cell

PEM电解制氢的核心部件是膜电极组件(membrane electrode assembly,MEA),它由质子交换膜、阴阳极催化层和阴阳极扩散层组成。催化层是电化学反应发生的地方,通常使用铂或铱等贵金属作为催化剂。扩散层是集流板和催化层之间的中间层,它起到传递水、气和电流的作用。集流板是端板和MEA之间的导电部件,它起到分配水、气和电流的作用,并提供机械支撑。电化学反应发生在三相界面,即质子交换膜、催化剂和水三者的交接处[12]。质子交换膜是一种高分子材料,多采用Nafion膜,起着隔离阴极和阳极的重要作用。质子交换膜具有选择透过性,能够传导质子,但阻隔电子和气体的传递。当通电后,水电解成氢离子(H+)和氧离子(O2-),氢离子通过质子交换膜传递到阳极,与电子结合生成氢气;氧离子通过阴极在电子的参与下生成氧气,其化学反应式如式(1)-式(3)所示:

阴极:

4H++4e-→2H2

(1)

阳极:

(2)

总反应:

(3)

具体而言,在质子交换膜电解槽工作工程中,在输入电力和催化剂的作用下,水分子在阳极被分解为氧气、H+以及电子e-,H+和水分子结合成水合离子H3O+,在电场作用下穿过薄膜到达阴极,与此同时电子通过外部电路离开电解槽传输到阴极,水合离子H3O+与电子e-在阴极与溶液界面处发生还原反应生成氢气。质子交换膜中的氢离子是通过水合氢离子形式从一个磺酸基转移到相邻的磺酸基,从而实现离子导电。

PEM电解制氢系统由电解槽、水泵、分水器、换热器、电源等多个设备组成,电源为电解槽供给电解所需的直流电[7],电解和冷却所需的水由循环水路进入电解槽,该系统的原理与结构如图3和图4所示。电解后,循环水和氧气从氧气出口流出,经过气水分离装置使水和氧气分离,分离出的液态水进入水循环,进行水质处理后,在循环水泵驱动下,重新由电解槽氧侧入口进入电解槽,以此形成循环。随着电解水的不断消耗和循环过程中水的蒸发,当水量减少至分离器低水位时,通过补水泵补充水量,以保证系统持续循环。电解槽产生的热量,由循环水携带而出,经换热器进行冷却。电解水产生的氢气从氢气出口流出,同样经过气体分离装置,分离后得到的高纯度氢气储存到储氢罐中。PEM电解制氢系统的运行过程是一个高度复杂的过程,其中电、热、氢三者之间相互耦合密切。电流的变化会直接影响氢的产量以及系统内部的热释放,热的产生和分布则会对系统的温度产生重大影响,而温度变化又会反过来影响电解效率。与此同时,氢的生成量会影响储氢罐中的压力,这也会对电解效率和系统的散热过程产生影响。因此,为了全面地理解和准确地预测PEM电解制氢系统的性能,必须建立一个综合性的系统模型,以充分考虑电、热、氢三者之间的复杂耦合关系,更好地揭示PEM电解制氢系统内在的物理过程。

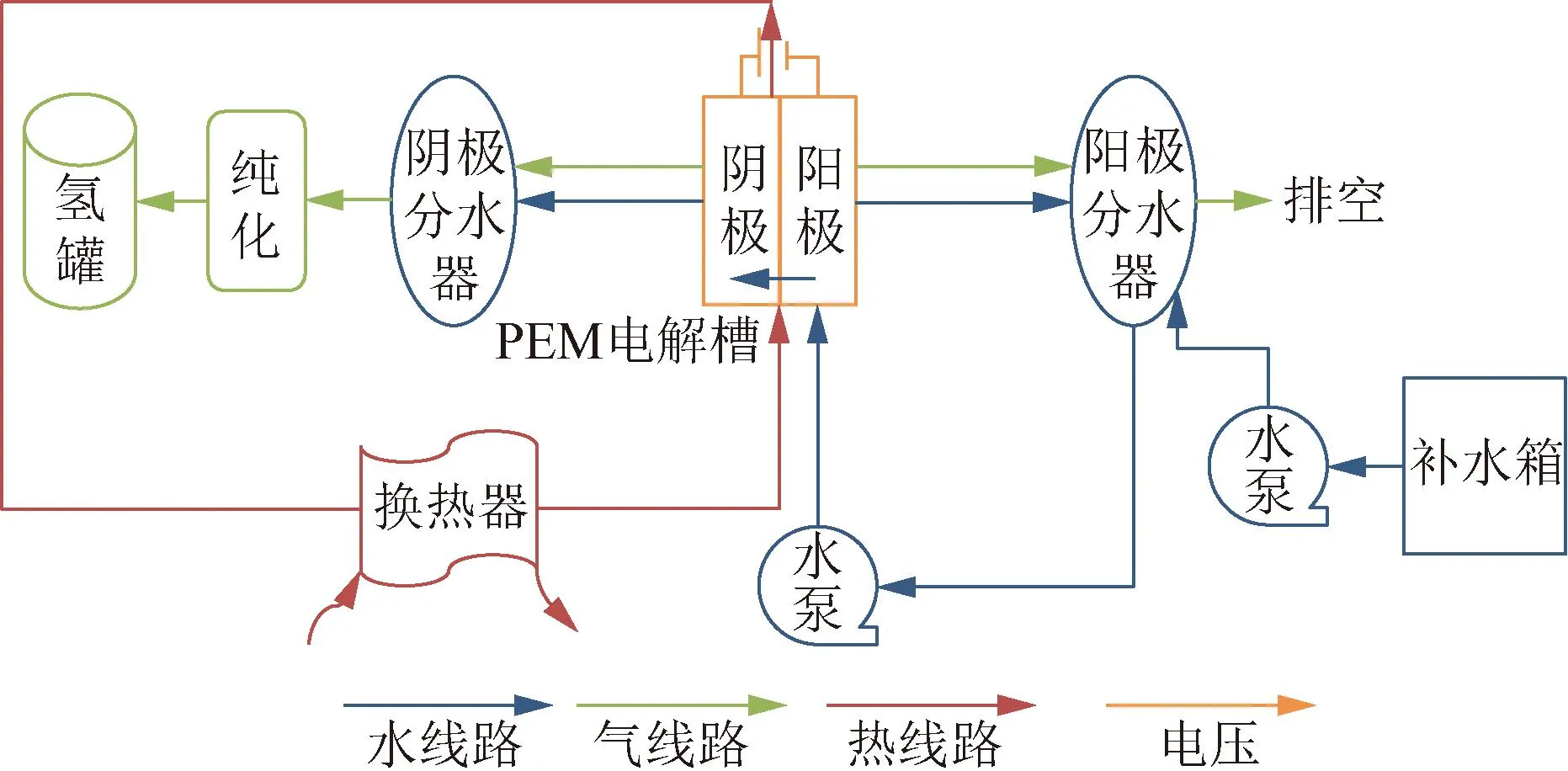
图3 PEM电解制氢系统原理Fig.3 Principle of PEM electrolysis hydrogen production system

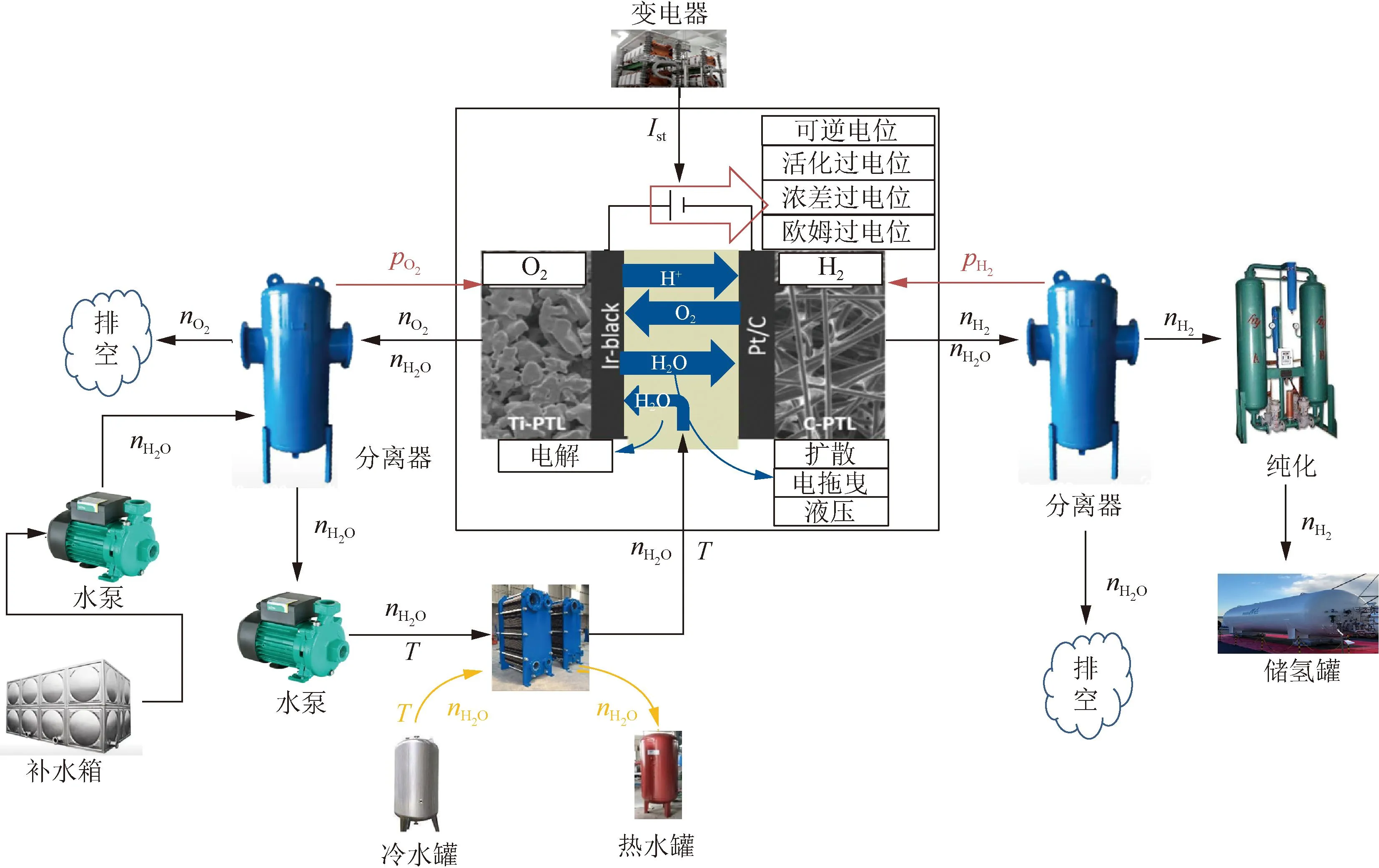
图4 PEM电解制氢系统结构Fig.4 Structure of PEM hydrogen production electrolysis system

2 PEM电解制氢系统模型

PEM电解制氢系统模型的建立从建模尺度角度,可分为单电解池/槽建模、系统多尺度建模;从运行状态角度,可分为静态模型、动态模型;从建模方法角度,可分为机理模型、经验模型及半经验模型;从学科领域角度,PEM电解制氢系统涉及电化学反应、传热传质、机电调节等多个领域。考虑到PEM电解制氢系统是一个水-热-电-气交叉耦合的复杂系统,本文将从单电解池/槽模型入手,基于电化学动力学、电极动力学、能量及物质平衡以及水/气在膜中传输等原理,解析内部涉及的电压损失、水传输等过程,并考虑电解槽与辅机系统的能量、物质动态传输过程,从水、热、电、气四个方面,对电解制氢全系统的建模展开阐述。

2.1 电解槽模型

2.1.1 电压模型

为了评估和优化电解槽的性能和效率,需要对其进行数学建模和仿真分析。其中一个重要的指标是电解槽的极化曲线,它描述了在不同的工作条件下,电解槽的总电压与通过其两端的电流密度之间的关系。极化曲线可以反映出电解槽内部发生的各种物理和化学过程,以及它们对产氢速率和能耗的影响。电解槽一般工作在电流模式或电压模式。当它在电压模式下运行时,一个电压源连接到电解槽上,电解槽根据工作条件从电压源中获取电流,经过几个瞬态循环后,达到稳定状态。但考虑到进入电解槽的电流通常是可控的,且电流模式运行通常便于提供一个稳定的产氢状态,所以市面上大多数商业上可用的电解槽在电流模式下运行,电解槽的工作电压根据电流计算。电解槽的工作电压组成如图5所示,其外部施加的总电压等于内部产生的各种分量之和,如式(4)所示[13-16]:

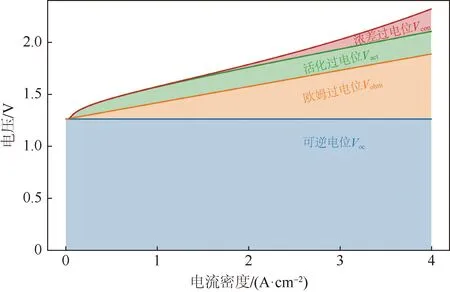
图5 电解槽工作电压组成Fig.5 Composition of electrolysis cell operating voltage

V=Voc+Vact+Vohm+Vcon

(4)

式中:V为工作电压;Voc为可逆电位,又称开路电压,即在没有电流通过时,由于电解槽内部的化学反应产生的电势差;Vact为活化过电位,即由于电解槽内部的反应动力学限制造成的电压损失;Vohm为欧姆过电位,即由于电解槽内部的电阻和接触阻抗造成的电压损失;Vcon为浓差过电位,即由于电解槽内部的质量传递限制造成的电压损失。这四个分量都与电解槽的内部状态和外部条件有关,可以用不同的数学模型来表示和计算,将在下文中详细介绍。

1)可逆电位。

可逆电位是指在没有任何极化损失的理想情况下,电解槽两端所需施加的最小电压,以使水分解为氢气和氧气。可逆电位是由水电解反应的热力学性质决定的,与电解槽的结构和材料无关。根据上节所述的水电解反应的总反应方程式(3),可以利用能斯特方程来计算可逆电位。能斯特方程是一个描述化学反应平衡时,反应物和生成物之间电势差的方程。对于水电解反应,能斯特方程可以写成如式(5)形式[17-21]:

(5)

式中:E0为标准参考电势,即在标准状态下(温度为298.15 K,压力为101.325 kPa,浓度为 1mol/L),水分解为氢气和氧气所需的最小电压,其值为1.23 V;R为气体常数,其值为8.314 J/(mol·K);T为反应温度;F为法拉第常数,其值为96 485 C/mol;PH2、PO2为氢气、氧气的压力;aH2O为电极与质子交换膜之间水的活度,即水在混合溶液中的有效浓度,其数值通常近似于1。

根据式(5)能够计算在特定条件下的可逆电位,是电解反应的重要参数之一。可逆电位反映了电化学反应的热力学特性,对于理解和优化水电解过程非常重要。可逆电位与温度、压力和水活度有关。当温度升高时,可逆电位降低;当压力增大时,可逆电位升高;当水活度减小时,可逆电位降低。在实际应用中,可以通过测量相关参数来计算或估算可逆电位,以更好地控制和优化电解槽的性能。

2)活化过电位。

活化过程是指在电解槽中发生的两个半电极反应,即阳极上的水分解为氧气和质子,阴极上的质子还原为氢气。活化是由发生在电极表面的、反应缓慢的动力学特性引起的。活化过电位是指能量在转化过程中会不可避免地发生一些不可逆损失,其作用在于推动电子在化学反应中移动到或者离开电极表面。这个电势损失是由于电子的转移过程中存在的储能和释放能的不均衡所引起的。活化过电位在电化学领域中具有重要作用,因为它代表了电极表面发生反应的速率,从而影响了整个电化学反应的动力学行为。活化过电位通常用电极表面阳极和阴极反应的Butler-Volmer(B-V)方程来描述,该方程考虑了在半电极反应中发生的正向和逆向的电荷转移反应动力学,如式(6)所示:

(6)

式中:I为电流密度;CPE、CPS为靠近电极和电解液中的产物浓度,其中产物在阳极中为O2,在阴极中为H2,如式(1)-(2)所示;CRE、CRS为靠近电极和电解液中的反应物浓度,其中反应物在阳极中为H2O,而在阴极中为H+,通常不考虑其活化极化,即认为CRE/CRS=1;αk为发生在半电极反应上的传递系数;I0,k为半电极反应上的交换电流密度,即在平衡状态下正向和逆向反应相等时产生或消耗的最大电流密度;z为电极反应参与的电子数。

为了得到活化过电位随电流密度的函数表达式,假定试样中的浓度和三界接触附近的浓度相等,即在不考虑浓差引发的过电位时,CPE、CPS、CRE、CRS取值相等可以约去,式(6)简化如式(7)所示:

(7)

假设电子转移过程对称,电荷分布均匀,即电荷传递系数等于0.5,公式变形如式(8):

(8)

当电荷转移系数取值0.5时可以采用上述B-V方程计算活化过电位[22-23],但陈锦洲等人[24-27]并不认同电荷传递系数取值0.5的观点,他们对上述公式进行变形,在公式中引入电荷转移系数变量,变形如式(9)所示:

(9)

式中:i0,an和i0,cat分别为阳极和阴极的交换电流密度;αan为阳极电荷传递系数;αcat为阴极电荷传递系数。

式(6)为原始浓度依赖Butler-Volmer方程,最具普适性,能描述各类电极过程,但与浓度耦合增大了求解难度。式(7)为标准Butler-Volmer方程,反应物充足时具广泛适用性,实现浓度解耦,电流与电压显式,易求解,电解研究中较常用。式(8)为简化Butler-Volmer模型,可直接获电压-电流解析表达,计算最简单,可用于对称反应或初步估算。式(9)在(8)基础上加入对称系数,电压对电流显式,电流对电压隐式,扩展了模型适用范围。这些模型具有不同适用性和复杂度,应根据具体问题和求解需求选择。通常式(6)最通用但复杂,PEM电解时反应物充足,式(7)较常用,其他公式在特定情况下提供更简单求解和估算。

不同文献报道的交换电流密度的值是不同的。通常电流密度值随温度的增加而增加,出于这个原因,Alhassan Salami Tijani等人[28]为了更好地调整他们的模型,提出了一个将交换电流密度与温度联系起来的表达式,具体公式如式(10)-(11)所示:

(10)

(11)

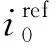
交换电流密度值对活化过电位有很大的影响,在很大程度上取决于电极的材料和孔隙率、催化剂颗粒的浓度、分布和尺寸以及操作温度[29]。不同文献中阴阳极交换电流密度及电荷传递系数不同取值见表1[28,30-41]。

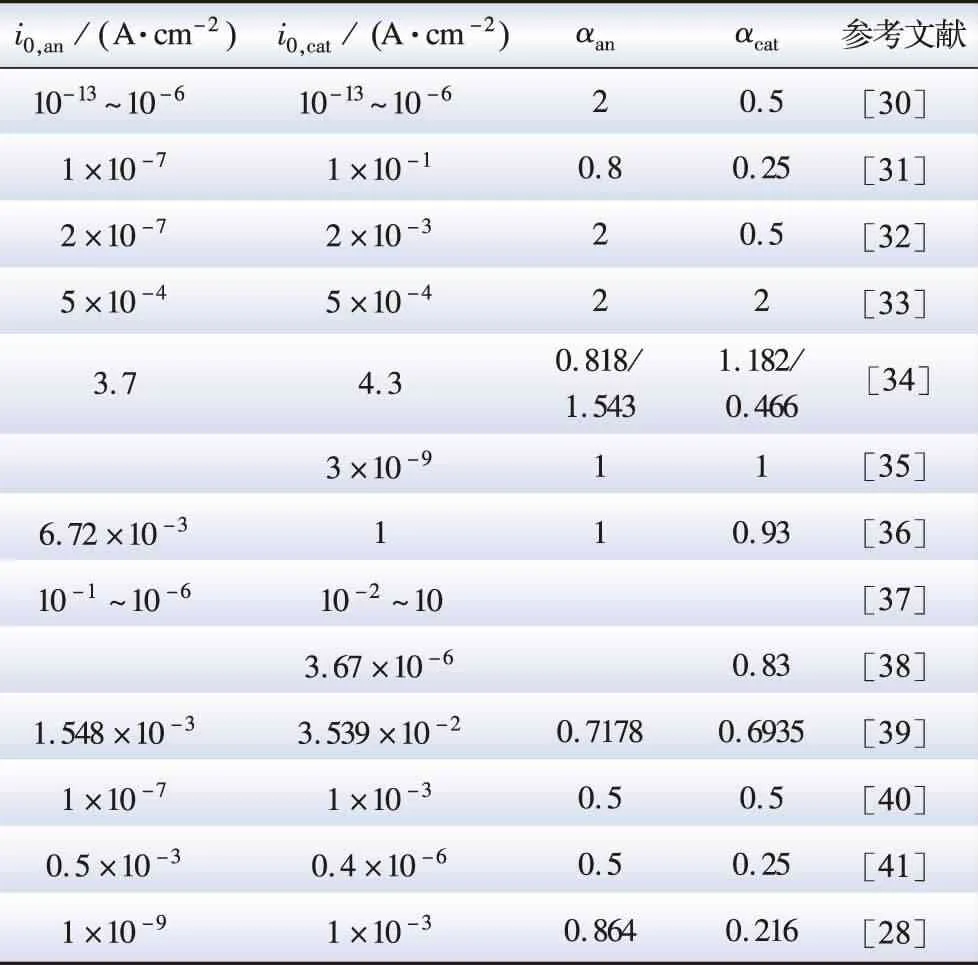
表1 阴阳极交换电流密度、电荷传递系数取值Table 1 Value table of exchange current density and charge transfer coefficient in anode and cathode

此外,Pierpaolo Polverino等[42]人建立了交换电流密度与催化剂相关的公式,如式(12)-(13)所示:

(12)

kECSA=sPt·wPt·uPt

(13)

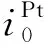
通过式(12)与式(13),可以更好地建立起交换电流密度与温度、催化剂之间的关系,表征温度变化、催化剂含量对交换电流密度的影响。

活化过电位是电解槽性能的重要指标。通过优化电催化剂的结构、组成和活性位点,可以提高半电池反应的交换电流密度,降低活化过电位,提高电解槽的产氢效率。

3)欧姆过电位。

欧姆过电位Vohm是指在电解槽中,由于各部件存在一定的内部阻抗,导致总体极化曲线呈现出线性特征的一种极化损失。欧姆过电位是由于电极、双极板和质子交换膜的欧姆电阻而产生的[41]。欧姆损耗的大小取决于材料的性质与各部件的结构尺寸,制造技术和工艺是降低欧姆过电位的一个重要方式。欧姆过电位计算采用欧姆定律,C Marr等人[43]提供了一种计算欧姆过电位的公式,Meng Ni等人[44-48]在其公式的基础上简化如式(14)所示:

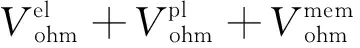
(14)

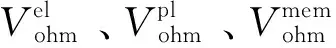
各部件电阻可以根据材料的性质和各部件的结构尺寸来计算或测量得到。Z Abdin等人[31]进一步通过电路类比法,得到了与电子通过电极和双极板传递有关的过电位。将欧姆定律应用于电极和双极板,如式(15)-(16)所示,得到:

(15)

(16)

式中:Rel,pl为电级和双极板的欧姆电阻;l为电子通道长度,即电极和双极板的厚度;A为电子通道的横截面积,即电极和双极板的有效导电面积;ρel为电极、双极板的电阻率,即材料的本征导电性,;ρeff为电极、双极板的有效电阻率,即考虑了材料的孔隙率后的实际电导率;ε为电极的孔隙率。

质子交换膜的欧姆过电位是由于质子在膜中传递所产生的,可以用欧姆定律的形式表示,见式(17)。PEM电解槽的膜电导率可以用膜含水量λ表示[41,49],如式(18)所示:

(17)

(18)

式中:i为电流密度;δmem为质子交换膜的厚度;σmem为质子交换膜的电导率;λ为膜含水量。

膜电阻占比最大,一些文献[22,24]中用膜电阻带来的电压损失来近似表示整个欧姆过电位。然而,质子交换膜的导电性受到其含水量的影响,而含水量又受到温度、压力、湿度等因素的影响。对于含水量计算,PEM电解槽导热系数与含水量有关,不同条件下含水量也不同。标准膜制备(在氧化的酸性水溶液中将膜加热到90 ℃)使膜在干燥条件下的含水量λ约为0.5,在饱和水气体(100%湿度)下的含水量为12～14,在液态水下的含水量约为22[50-51]。除了将含水量看作常数代入公式,还可以通过水蒸气的活度间接求出,具体如式(19)-式(20)所示:

λ=0.043+17.81a-39.85a2+36a3

(19)

a=P/Psat

(20)

式中:a为水蒸气的活度,假设气体混合物表现为理想气体,水蒸气的活度可以用相对湿度代替,相对湿度是指空气中水蒸气的实际压力P与饱和水蒸气压Psat之比。

4)浓差过电位。

浓差过电位是指在电解过程中,由于反应速率快于质量输运速率,导致电极表面反应物浓度降低,生成物浓度升高,从而使得反应动力学受到抑制的一种极化损失。浓差过电位是由于电解过程中电极表面反应物浓度的变化而产生的。当电流密度足够大时,反应分子过多会阻碍反应物进入活性位,从而减慢反应速率,产生质量输运损失,这种现象被称为质量传输限制。在PEM电解槽中,水分解为氧气和氢气的反应速率很快,而水和气体在膜和催化层中的扩散速率相对较慢,浓差极化一般发生在高电流密度的情况[52]。

为了预测由于催化层部位反应产物过剩而阻塞反应物造成的浓差过电位,通常采用能斯特方程结合菲克定律来描述高电流密度下限制反应速率的扩散速率Vcon[30]。这种方法称为扩散驱动方法,具体如式(21)所示[11]:

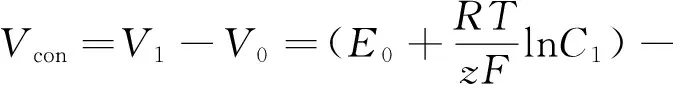
(21)

式中:V1为工作条件下电极电势;V0为参考工况下电极电势;E0为能斯特电势;C1为界面膜电极处氧气或氢气的浓度;C0为参考工况下的工作浓度,也作为参考浓度;z为反应过程中转移的电子数。

综上,PEM电解制氢系统中电解槽的电压模型主要通过综合电解槽参数及其系数的物理关系和经验关系,由式(4)-(21)来表示。运用上述公式建立的电压模型参数较少,降低了模型的复杂性,可以较为容易地集成到仿真软件中,便于模型建立及优化设计。但也有一些不同建模方法,具体公式见表2。

表2 电压模型其他建模Table 2 Other voltage models

表2中:ηAn和ηCa分别为阳极和阴极的活化过电位;rPEM、rAn和rCa分别为质子交换膜、阳极、阴极的欧姆电阻;ηcorr为过电势矫正系数;Tel为电解质温度;Re和Rp分别为电极;Aa和Ac分别为阳极和阴极的活化过电势对称系数;Re和Rp分别为电极和双极板的欧姆电阻;ρeff为电极的等效电阻率;wc为流道宽度;ws为电极肋宽;ng为流道数量;δe为电极厚度;L为电极长度;ρp为双极板电阻率;hp为双极板高度;hc为流道高度;W为双极板宽度;ilim为极限电流密度。

具体地,对于电解槽电压公式,除了公式(4)外,Ozcan Atlam[53]也提出了电解槽电压的经验公式,建立了电压非线性模型;对于可逆电位E0,通常取值为1.23 V[54],但这只是在标准温度和压力下的理想取值,结果并不准确,Vesa Ruuskanen等人[39,55-58]采用温度经验公式完善可逆电位的计算方法,提高了模型的准确性;对于活化过电压,几乎所有的作者都使用基于Butler-Volmer方程的表达式来描述活化过电位,但是也有例外,C.Y.Biaku等人[59-60]使用Tafel方程来描述计算活化过电位;对于计算电极、双极板的欧姆过电位,一般采用式(15)-(16)简化计算,但是电极和双极板中电子传播方向不同,在计算电阻率的时候往往不能很准确地计算电子通道长度,以及电子通道的横截面积,误差相对较大,C Marr等人[43]提出一种新的方法,把电极双极板根据孔道划分成若干部分,在分别计算每部分的电阻,从而分别细化了电极和双极板的欧姆过电位计算方法,虽然模型更加精准但是建模方法复杂;对于浓差过电位,式(21)描述了浓差过电位的建模方法,实际实验中,在高电流密度条件下,浓差过电位随着温度、压力增加浓差过电位将增大[37,39],但是在低电流密度条件下,浓差过电位可以忽略不计,因此,在大多数文献中,尤其是在低电流密度下的仿真建模中,很多作者都选择忽视[61-63]。当然,浓差过电位还可以通过极限电流密度计算建模,Eng Waseem Saeed[64]通过提供给电解槽的最大电流密度,揭示了电解槽允许的最大速率。

未来可以从以下几方面进行进一步研究:开发能综合不同模型优点的新型电解槽电压模型,既考虑准确度,又考虑模型简洁性与仿真易用性;加强对影响电解槽电压的各种参数与过程的深入理论研究,以建立更科学合理的模型表示;扩大模型的适用范围。目前多数模型局限于某一操作条件下,可以探索建立适用于更广泛条件的通用模型;加强模型的实验验证和优化调整。现有模型大多依据有限数据建立,可以通过更系统和丰富的实验数据进行验证和修正;开发易于集成到多尺度多物理场耦合模型中的电解槽电压模型。这对实现从分子尺度到系统尺度的多层次仿真分析很有必要;应用先进的机器学习和大数据技术,开发数据驱动的电解槽电压模型,这可以弥补经验模型的不足。总体来说,电解槽电压模型是电解槽模型中应用范围最广、最重要的模型之一,其研究还有很大改进空间,需要各方面不断努力,进一步提高其在实际工程应用中的价值,从而推动氢能源技术的发展。

2.1.2 膜水合模型

膜水合模型主要用于表征阴阳极间通过膜传输水的过程。由于PEM电解槽中的质子交换膜具有一定的透水性,因此在电解过程中,会有一部分水从阳极侧通过膜传输到阴极侧,或者从阴极侧通过膜传输到阳极侧。这种水的传输会影响电解槽的性能和效率,因此需要对其进行建模和分析。通过膜的水流量可由电渗透、扩散和压差三个部分引起的流量变化计算,如式(22)所示:

(22)

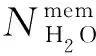
1)电渗透。

电渗透是指在电场作用下,带有正电荷或负电荷的溶质分子或离子带动溶剂分子或离子一起移动的现象。在PEM电解槽中,由于质子交换膜上存在一个横向电场,使得带有正电荷的H3O+离子在迁移过程中带动一定数量的水分子一起从阳极侧向阴极侧移动。电渗透进入阴极的水含量是阳极通过膜进入阴极水的主要组成部分。通过膜电渗透进入阴极的水摩尔流量与水合质子通过膜从阳极向阴极迁移的通量直接相关,因此其摩尔流量由式(23)所示[32,65-66]:

(23)

式中:nd为电渗透系数,定义为水的摩尔数比氢离子摩尔数,表示每个氢离子带动的水分子数,即nH2O/nH+。

PEM燃料电池模型发表的文献较多,nd值已经被报道。无论是PEM电解槽还是PEM燃料电池,电渗透系数均是与穿过质子交换膜的水摩尔数和氢离子摩尔数有关。所以可以借鉴燃料电池中给出的nd值,缩小取值范围,具体如表3所示[30-31,67-68]。

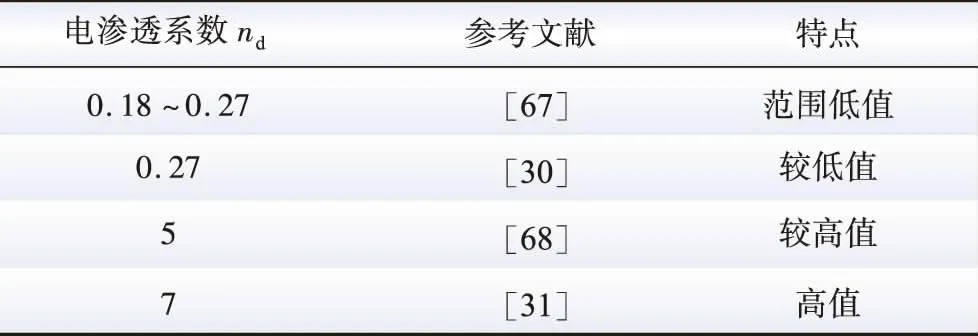
表3 电渗透系数取值表Table 3 Value table of electric permeability coefficient

2)扩散。

扩散是指在PEM电解槽中,由于阳极侧和阴极侧存在着不同程度的水汽饱和度,因此会有一部分水汽从高饱和度处向低饱和度处扩散,从而导致阳极侧的水损失和阴极侧的水增加的现象。Z Abdin等人[31]采用菲克扩散定律进行计算由阳极通过扩散进入阴极的水含量。菲克扩散定律是指在稳态条件下,溶质分子或离子沿着浓度梯度方向自发地移动,从而使浓度趋于均匀。通过对两膜界面间的菲克扩散定律积分,计算了由扩散引起的水的摩尔流量,具体公式如式(24)-(28)所示:

(24)

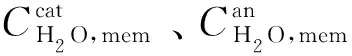
(25)

(26)

(27)

(28)

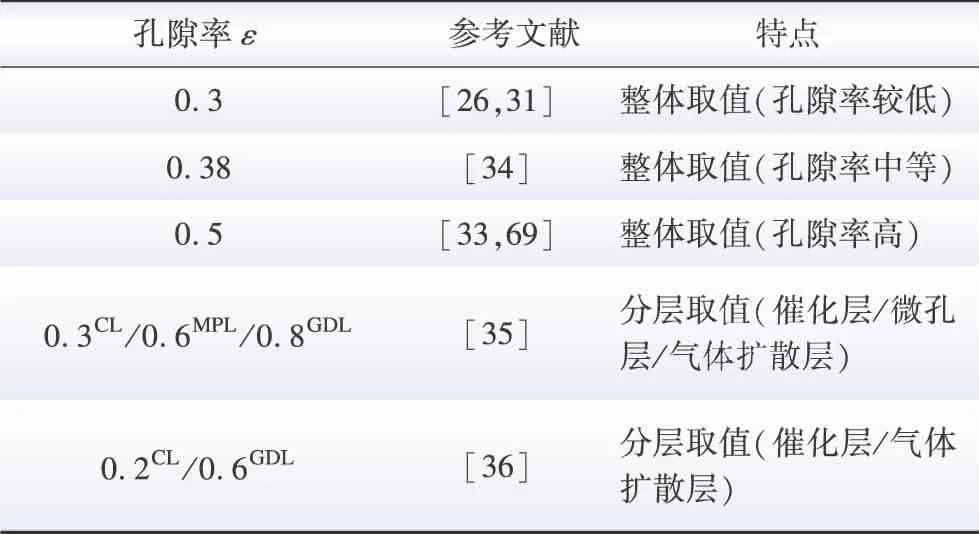
表4 孔隙率取值表Table 4 Value table of porosity

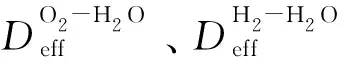
(29)

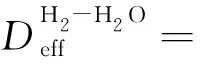
(30)

式中:Pan、Pcat分别为阳极、阴极压力;MO2、MH2、MH2O分别为氧气、氢气、水的摩尔质量;σO2-H2O、σH2-H2O分别为O2-H2O、H2-H2O分子半径;ΩD为扩散碰撞积分。

3)压差。

压差是指在PEM电解槽中,由于阳极侧和阴极侧存在着不同的气体压力,因此会有一部分水从高压处向低压处流动,从而导致阴极侧的水损失和阳极侧的水增加的现象。水通过膜从阴极到阳极的传输速率也取决于压力梯度,考虑到膜的渗透性,文献中通常用达西定律来评价这一现象,在压差作用下水从阴极到阳极的摩尔流量可表示为式(31):

(31)

式中:KDarcy为达西系数,取值为1.58×10-14m2[30-31,33];ρH2O为水的密度;ΔP为阴极阳极压力差值;μH2O为水的粘度,不同文献取值不同,如 F Marangio等人[30]取值为1.1×10-3Pa·s,Qiangqian Wang等人[35]取值为1.211×10-4Pa·s。

综上,阐述了膜水合模型的建模方式,在膜水合模型中还存在一些不同建模方法,具体公式见表5。如:对于电渗透,电渗透公式(23)中nd并不是常数,它与阴极压力、电流密度、湿度、温度、孔隙率和弯曲度有关[72],但是现在多数作者通常并不是通过膜的湿度、温度求电渗透系数,而是在讨论结果时通过和电解槽极化曲线的吻合程度去单独设定调整nd值,建立经验公式;也可以通过其他方法求得nd,W K Lee等人[69]将nd与膜的加湿程度成比例地联系起来,Xiaojin Li等人[73]通过引入温度进行估算。对于扩散,分子有效二元扩散系数不仅公式(29)-(30)一种表达方式,Dawn M Bernardi等人[33,43]通过孔隙率从微观角度化简方程,Rui B Ferreira等人[36]通过宏观角度简化成和温度、压力有关的关系式。

表5 膜水合模型其他建模Table 5 Other Membrane hydration models

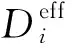
对电渗透系数nd的建模,目前多通过经验拟合,还未充分考虑其与操作条件的关系。nd的准确表达对提高模型精度非常重要。建议基于理论研究nd的影响因素,并通过大量实验数据求取nd的准确表达式。还可以考虑建立不同复杂度层次的nd模型,兼顾精度和计算量。

对扩散系数的建模也存在微观和宏观方法的区别。两种方法都有各自的优势,建议根据具体情况选择合适的模型。此外,扩散是一个复杂的空间分布过程,当前均匀参数的模型可能过于简化,建议开发反映非均匀性的模型。

总体而言,膜水合过程高精度模型建立还面临如下挑战:理论研究不够深入,对过程机理的理解还不充分;实验数据不足,许多参数难以准确确定;模型过于简化,许多细节特征未考虑;与其他物理场的耦合不足。

下一步研究建议:设计更系统的实验方案,获取充分可靠的数据;加强多物理场耦合,建立整机协同模型;应用新方法建立数据驱动的模型。

2.2 系统水路模型

PEM电解制氢过程中,水作为反应介质和产物,其传输过程对系统的性能和安全性有着重要影响,水传输是电解槽正常运转的关键。一方面,水路系统为电解槽提供反应原料水,使得电解制氢系统正常运转。另一方面,合理设计水路能够更有效地提高设备利用率,节约成本。因此,对水传输过程的建模和分析是PEM电解制氢系统设计和优化的关键步骤。众多文献建立了系统水传输模型,用于反映电解制氢系统水传输随时间的变化过程。电解制氢中水传输过程主要包含电解槽用水供给、电解制氢后气水分离等过程,涉及的辅件主要为水泵、分离器、水箱,下文将分别介绍水泵、分离器、水箱的建模方法。

2.2.1 循环水泵模型

循环水泵用于供给电解槽用水,通过循环水泵可以调节进入电解槽的水流量。Tevfik Yigit等人[32]针对循环水泵提出了一个基于电机转速和水流量之间关系的数学模型。该模型考虑了电机和水泵之间的耦合效应,以及电机内部的电气和机械参数。该模型由四个微分方程组成,分别描述了电机的电路、转矩、角速度和水流量之间的动态关系。通过该模型,可以根据给定的输入电压和输出水流量,计算出相应的电流、转矩和角速度,并进行相应的控制策略设计。该模型如式(32)-(35)所示:

(32)

τm(t)=Kiia(t)

(33)

(34)

(35)

式中:ia为转子电流;Ra为转子电阻;Va为转子电压;Vb为定子电压;La为转子电感;τm为转子转矩;τL为电磁转矩;Ki为转子转矩常数;Kb为定子转矩常数;Bm为粘摩擦系数;θm为转子位移;Jm为电动机惯性;ωm为转子角速度。

在PEM电解槽等系统中,需要确保水的精确供应,以维持反应的稳定性。该模型简单易实现,只需要测量输入电压和输出水流量即可得到其他参数的估计值。模型使用与电机转速相关的水泵模型能够直接控制水流量,反映出电机转速与预期水流量之间的线性关系,使其与电机的运行状态同步,便于进行闭环控制。这样有助于确保在PEM电解槽等应用中的水流控制更加精确和可靠,因此该模型在这些领域具有重要的实际价值。但是也存在一些局限性,模型假设电机和水泵之间完全耦合,没有考虑到可能存在的滑动或松动等现象,可能影响模型的精度和稳定性。

2.2.2 分水器模型

分水器是一种能够将混合的气体和液体进行有效分离的装置,它在PEM电解制氢系统中起着重要的作用。在PEM电解制氢系统中,电解槽输出的双相流包含了氢气、氧气和水三种成分,其中氢气和氧气是有价值的产物,需要被收集和储存,而水则需要被回收和循环利用。因此,对双相流进行合理的分离和管理是提高系统性能和安全性的关键。

在PEM电解制氢系统中,每个电解槽都配备了两个分水器,一个位于阳极侧,用于将阳极输出的含氧双相流进行分离,另一个位于阴极侧,用于将阴极输出的含氢双相流进行分离[57],模型如图6所示。这两个分水器的结构和工作原理类似,都是利用重力和压差等物理原理,使得不同密度和状态的物质在容器内发生自然沉降和上升的过程。通过控制容器内的液位高度、截面积、进出口流量等参数,可以实现对气体和液体的有效分离和输出。

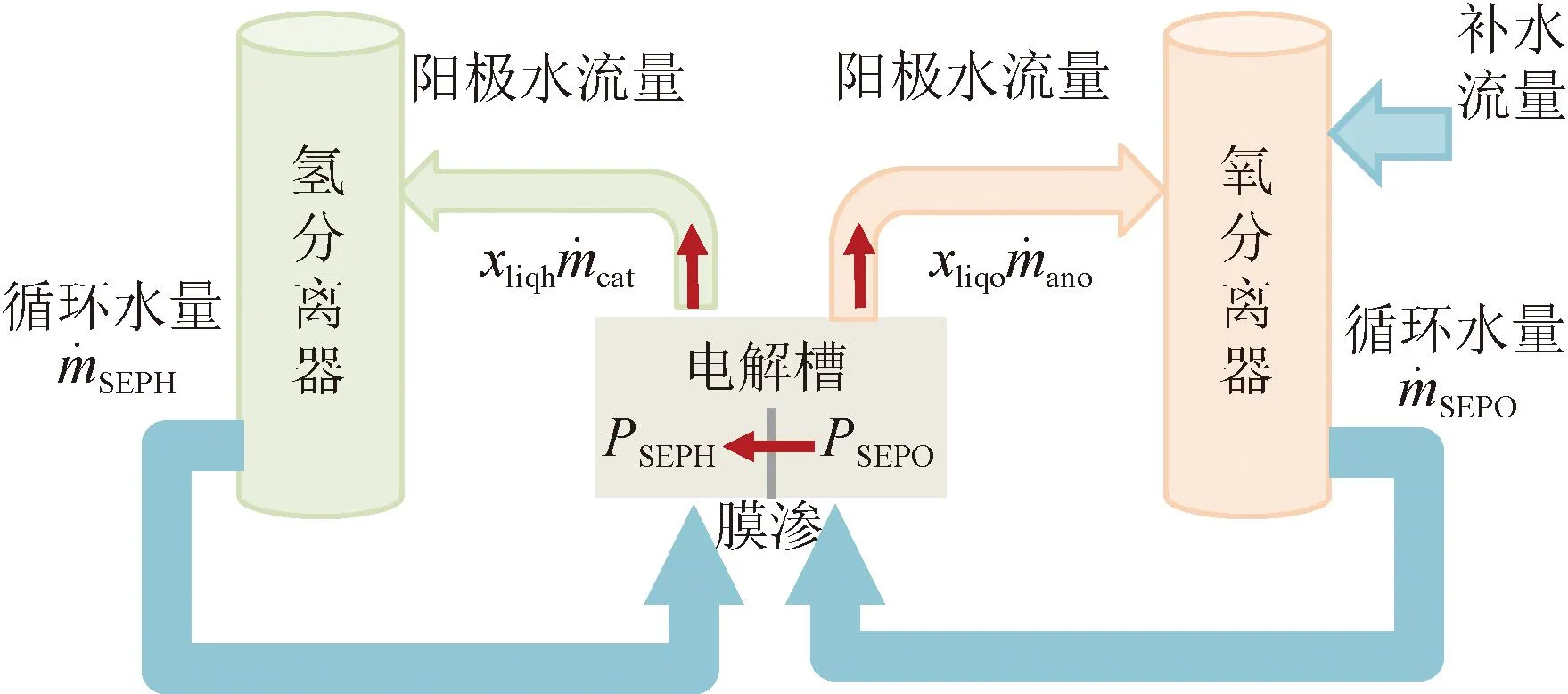
图6 氢/氧分水器模型Fig.6 Hydrogen/oxygen separator model

为了描述分水器在PEM电解制氢系统中的动态行为,需要建立相应的数学模型。模型基于质量守恒基本原理,来表示分水器内液位高度和流量之间的关系。氧分离器的数学模型,如式(36)所示,可描述为:

(36)

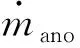
氢分离器的数学模型,如式(37)所示,可描述为:

(37)

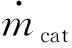
该分水器的数学模型对于PEM电解槽等应用具有重要意义,因为它们有助于准确控制氧气和氢气的输出流量,从而维持反应的稳定性和效率。因此,模型在氢/氧与水分离的特定应用中非常适用。通过这些模型,可以根据电解槽的输出条件、分水器的结构参数和液位高度,计算出分水器的输出流量和压力,并进行相应的控制策略设计。

2.2.3 水箱模型

水箱用于电解用水的存储,在PEM电解制氢系统中起着缓冲和调节作用。,对于水箱来讲,合理的液位是保障系统安全可靠运行的关键,因此需要建立一个能够提供液位变化信息的水箱模型。水箱内的瞬时水位由进水流量和出水流量相减得到[32],如式(38)所示:

(38)

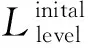
水箱模型在PEM电解制氢系统中扮演了重要角色,它的适用性在于确保液位控制、供水稳定性、应对突发情况和温度控制。这些因素对于PEM电解槽等应用的安全和高效运行至关重要。

综上,水路系统模型由式(32)-(38)来描述。其中水泵、分离器、水箱模型建模方法成熟,大多数均是采用该方法建模。该建模方法基本遵循了水力学和传质传热学的基本原理和计算公式,能够合理描述不同组件的水力/传质传热过程,因此总体上是正确的。然而仍需注意以下几点:水泵转矩模型可能过于理想化,应考虑转矩波动的影响;分水器模型应考虑气液两相流的相互作用;水箱模型应考虑水箱结构参数的影响。

在模型有效性方面,文献中的方法能够有效地模拟水路系统的动态变化,为系统控制和优化提供支持,但也存在一些可改进之处:可建立不同细节层次的模型框架,根据需求选择合适复杂度;可拓展模型范围,考虑更多实际水路构件的影响;优化模型的参数识别方法;可加强与其他子系统模型(如电解槽、散热系统)的耦合,进一步提高模型的准确性和适用性。

2.3 系统热传输模型

PEM电解制氢过程中,温度对整个电解槽的运行至关重要。提升运行温度,可以促进电解反应的动力学和传质过程,降低反应阻抗,系统能耗降低;但是通常电解槽的运行温度受限于膜等材料耐温,过高的运行温度会对膜等关键材料造成损伤或老化;同时随着温度升高,膜上氢气渗透现象,尤其是低电流密度下,将更加突出,带来安全隐患。因此,建立系统热传输数学模型,用于反映电解制氢系统温度随时间的变化过程,对于优化系统性能和保证系统安全具有重要作用。

热传输模型通常采用集总热容法,即将系统或其组件视为具有均匀温度的单一物体,并根据产热、散热和传热等过程建立热量平衡方程。根据不同的建模对象和目标,可以将系统划分为不同的子系统或单元,并考虑其之间的相互作用和影响。系统热传输模型的文章目前分为两种,一种是以电解槽为对象,系统热传输只考虑电解槽产热;另一种是以电解制氢系统为对象,除了考虑电解槽产热,水泵等辅机热回收也在考虑范围之内,下面将分别介绍两种模型。

2.3.1 以电解槽为对象建模

以电解槽为对象建模是一种只考虑电解槽内部的产热、散热和传热过程的系统热传输模型,如图7所示。它对于分析和控制电解槽的温度分布和变化具有重要作用。在PEM电解制氢过程中,由于反应的不可逆性和欧姆损耗等因素,电解槽会在工作时产生一定的焓变和焓损失,从而导致系统的温度升高。过高的温度会对膜等关键材料造成损伤或老化,降低系统的性能和寿命。因此,在设计和控制PEM电解制氢系统时,需要合理地控制和调节电解槽的温度。

图7 以电解槽为对象热传输模型Fig.7 Heat transfer model with electrolysis as object

通常电解槽工作在热中性电压(Utn)之上,这意味着电解槽在运行过程中将产生热量。根据能量守恒定律,电解槽产热量与热损失、散热量之和相等,R Garca-Valverde等人[74-76]基于电解槽内部的热平衡建立一个一阶线性微分热传输方程来表示电解槽的温度变化规律,模型如图6所示,其表达式如式(39)-式(41)所示:

(39)

(40)

(41)

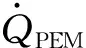
Cth=∑ρjVjCp,j

(42)

式中:ρj为组分j的密度;Vj为组分j的体积;Cp,j为组分j的比热容。

该模型考虑了电解槽生成热、散热系统散热和环境热损失三方面的因素。

1)电解槽生成热是指由于电解反应的不可逆性和欧姆损耗等因素,电解槽在工作时产生的热量。该模型假设产热量与电解槽的单片电压和热中性电压之差成正比,如式(40)所示。

2)散热系统散热是指由于系统的主动或被动冷却措施,电解槽向外界释放的热量。

3)环境热损失是指由于系统与环境之间的对流和辐射等方式,电解槽向环境散失的热量。该模型假设热损失量与系统的热阻和温度差成正比,如式(41)所示。电解槽热损失用热阻公式表示,热阻Rth可以根据电堆自然冷却时的热容和实测的热时间常数τth近似得到,也可以用电解槽外表面和整体对流辐射换热系数来近似计算,如式(43)所示:

(43)

以电解槽为对象的模型是一种简单而有效的描述PEM电解制氢系统中温度变化规律的数学模型,它对于分析和控制电解槽的温度分布和变化具有重要作用。该模型可以帮助我们理解和改进PEM电解制氢系统中的散热设计和控制策略。

2.3.2 以电解制氢系统为对象建模

以电解制氢系统为对象建模是一种考虑电解槽和其他辅助设备(如水泵、分离器、水箱等)的产热、散热和传热过程的系统热传输模型,如图8所示。它对于分析和控制整个系统的温度分布和变化具有重要作用。

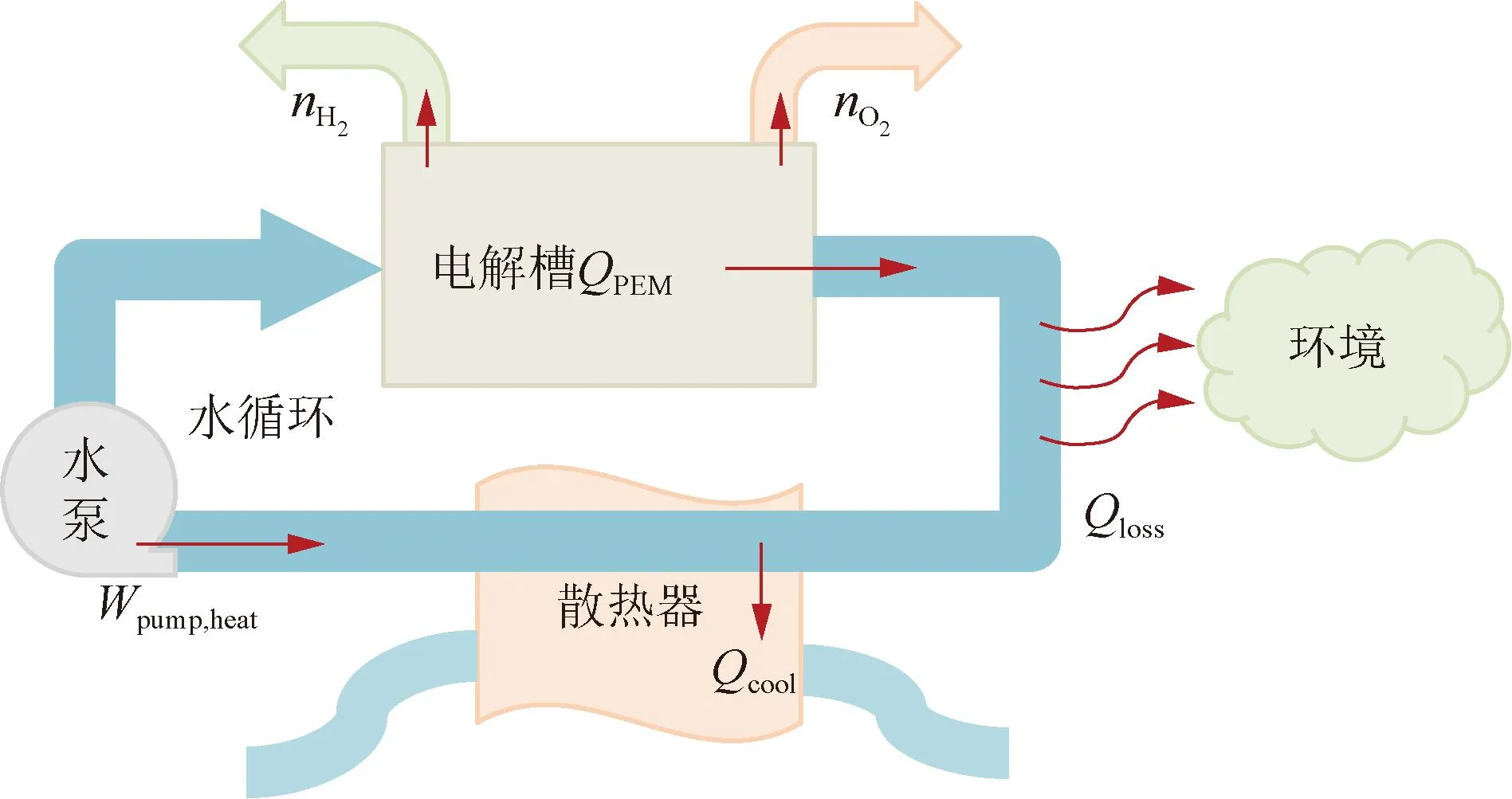
图8 以电解制氢系统为对象热传输模型Fig.8 Heat transfer model with electrolysis system as the object

Manuel Espinosa-Lopez等人[77-79]以电解制氢系统为研究对象,除了考虑电解槽产热,同时将水泵运行过程中产热以及生成气体与电解消耗水的显热也考虑进来,基于系统的热平衡,根据能量守恒定律建立一阶线性微分方程来表示系统的温度变化规律,建立了热传输模型如图8所示,其表达式如式(44)所示:

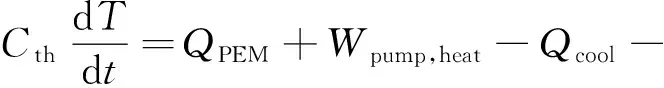
(44)

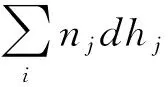
水泵产热是指由于水泵运行时消耗的电能部分转化为热能而产生的热量。该模型假设水泵产热量与水泵消耗的能量和水泵的效率之间有关,水泵产热计算如式(45)-(47)所示:

(45)

(46)

(47)

以整个系统为对象,不仅需要考虑电解槽产热,还要关注辅机产热。通过循环水流动将系统热量带走,经过换热器将换热后温度又重新回归初始温度,因此可以通过控制冷却水的流量,控制整个系统的温度。

综上,本节介绍了两种热传输模型,为了使热量计算更加精准,均考虑了热辐射对系统热量的影响,但Monica Sanchez等人[61]认为热辐射影响较小,直接默认为0。

文献中提出的建模方法遵循热力学第一定律,考虑了产热和散热的综合平衡,能合理描述热传输过程,仍可在以下方面进行改进:电解槽界面产热的空间分布非均匀性;水泵等设备的产热计算可再细化;散热系统模型可加强耦合。

目前无论是电解槽和系统模型都能够有效反映电解制氢过程中的热传输规律,为系统热管理提供支持,但仍可进一步优化,以实现高效的热管理。未来热传输模型可发展的方向包括:实现热传输机理的深入理解,建立多部件协同、多场耦合的精细模型;加强模型参数优化识别,提高热传输过程的预测精度。

2.4 系统电模型

系统电模型是一种用于描述PEM电解制氢系统中电力变化规律的数学模型,它对于优化系统性能和效率具有重要作用。虽然电解槽是电解制氢系统的主要组成部分,需要消耗大量的电能来进行水分解反应,但它不是唯一的电气设备。许多其他组件也需要电力的消耗与供给来进行运行或控制,如系统的执行设备(泵、电动阀、冷水机等)和变换器等。同时,为了提高系统的灵活性和可靠性,还需要考虑与外部电网或其他可再生能源(如风力发电、太阳能发电等)的连接和匹配,以及与储能设备(如蓄电池、超级电容等)的互动和管理,如图9所示。

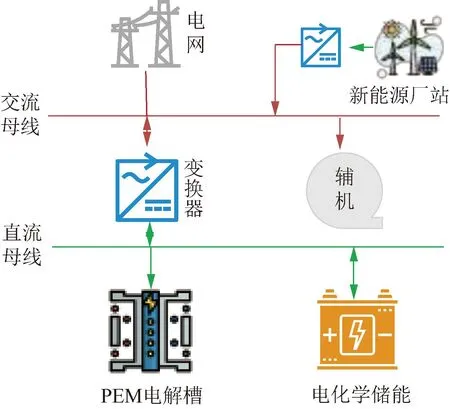
图9 电解制氢系统电模型Fig.9 Electric model of electrolysis system

下面将从变换器、其他辅机、电储能模型三个方面介绍电解制氢系统电模型。

2.4.1 变换器模型

变换器模型是一种用于描述PEM电解制氢系统中变换器的输入输出特性和效率的数学模型。每个电解系统都配备了变换器,以便使输入电流适应电解槽和其他电气设备的电流电压特性[80],从而保证系统的稳定运行和高效输出。由于变换器在转换过程中会有一定的损耗,文献中建立了变换器的效率模型,表示变换器中电能的变换,具体方法如式(48)-(50)所示[9]:

(48)

(49)

(50)

式中:Ps为转换器的输出功率;Pnom为额定功率;n0、m为系数;η为转换效率;η100为额定功率下的效率;η10为额定功率10%下的效率。变换器效率模型基于非线性模型,效率与输出功率之间的关系如式(48)所示,其系数可由10%和100%额定功率下的效率,根据式(49)和式(50)计算得到。

2.4.2 辅机功耗模型

辅机功耗模型是用于描述PEM电解制氢系统中除了电解槽之外的其他电气元件的电力消耗的数学模型。当考虑其他电气元件(如泵、冷水机等)时,可采用一个简单而通用的线性公式来表示其他电气元件的功率与电解槽的功率之间的关系。辅机电耗通常有两种表示方式,一是在电解槽运行时保持不变,辅机功耗只与系统启动后所消耗的恒定功率,适用于那些在系统运行过程中不随电解槽的运行状态而变化的其他电气元件,如循环水泵、风扇等;二是随电解槽功率线性变化,辅机功耗与系统启动后所消耗的恒定功率和电解槽的功率成正比,适用于那些在系统运行过程中随电解槽的运行状态而变化的其他电气元件,如冷却水泵、电磁阀等。因此它们可以用一个电耗公式表示PBOP,如式(51)所示:

PBOP=P0+k·Pstack

(51)

式中:P0为系统启动后所消耗的恒定功率;k为比例系数;Pstack为电解槽功率。暂时没有发现分别描述辅机功耗的详细模型。

2.4.3 电化学储能模型

在离网条件下,PEM电解制氢系统通常会采用锂离子电池作为备用电源。锂离子电池的荷电状态(state of charge, SOC)是指锂离子电池当前的剩余容量与其最大容量之比,锂离子电池电化学储能荷电状态模型如式(52)所示[81-82]:

Vd(t)=Vd(t0)+PcdμcdΔt

(52)

式中:Vd(t)、Vd(t0)分别表示在t时刻和t0时刻的电化学储能储电情况;Pcd表示电化学储能的充电功率;μcd表示电化学储能充电过程的效率。该模型假设锂离子电池的自放电率和内阻可以忽略,且充电效率与荷电状态无关。

除了锂离子电池模型,蓄电池也可以作为储能模块。蓄电池的剩余电量模型是一种描述蓄电池剩余电量随时间变化的数学模型,具体模型如式(53)所示[83]:

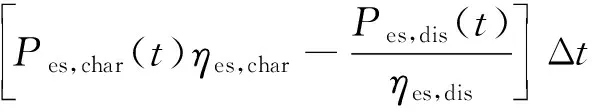
(53)

式中:Ees(t)表示t时刻储能电池的剩余电量;τes表示电池的自放电率;Pes,char、Pes,dis(t)分别代表t时刻储能电池的充放电功率;ηes,char、ηes,dis分别为储能电池的充放电效率系数。该模型考虑了蓄电池的自放电和内阻影响,且假设充放电效率与荷电状态无关。

综上,电路系统模型由式(48)-(53)来描述。所涉及的建模方法遵循了电路理论和电池充放电原理,能合理描述电路中的功率转换和储能过程,然而仍需注意以下几点:变换器效率计算可考虑更多影响因素;辅机功率变化可能不与电解槽呈线性关系;电化学储能模型可引入更多电化学动力学特征。

在模型的有效性方面,这些模型能够有效地模拟电路的动态变化,为系统优化提供支持。但也还有一些改进空间:与实际数据实现数字孪生,研究多目标功耗的设计与运行方案;提高对电化学过程和设备寿命与衰减的预测能力。

2.5 系统气路模型

系统气路模型是描述制氢系统中气体流量和压力变化的数学模型。PEM电解制氢过程中,在电解槽两侧分别产生氢气与氧气,氢气经过分离、纯化后进入储氢罐存储,氧气经过分离后排空或存储,如图10所示。

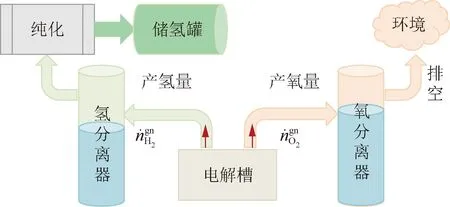
图10 电解制氢系统气路模型Fig.10 Gas flow model of electrolysis system

对于制氢系统,压力是其运行的关键,压力的高低影响系统的能耗,更重要地,压力的动态变化,对系统的安全、耐久运行十分重要,尤其是电解槽氢氧两侧的压差,对于常规的均压式电解槽,其大幅波动会引起催化剂脱落、膜机械变形等,建立气路模型,观测压力、压差的变化很有必要。同时,产氢量是制氢系统的关键输出性能,是系统气路系统建模的重点。

2.5.1 产氢量模型

产氢量模型是描述制氢系统中氢气产生量与电流、温度等因素关系的数学模型,用来评估制氢系统的性能、优化制氢系统的参数和控制制氢系统的运行。目前文献中,产氢量通常基于法拉第原理计算[84]。法拉第原理是指在一个闭合电路中,通过电解质所传递的电荷量与电解质中发生反应的物质的摩尔数成正比。根据法拉第定律,可以得到在给定的电流和时间下,PEM电解槽产生的氢气摩尔流量。然而,并非所有通过电解质的电荷都参与了水分解反应,因此需要引入一个修正因子,即法拉第效率,来表示实际产生的气体量与理论值之比。氢气摩尔流量可以用式(54)表示:

(54)

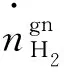
(55)

式中:Inom为额定电流。

在更高电流密度和更低温度下,ηF有望得到提高,R Garcia-Valverde等人[74]进一步考虑不同状态下损耗与动态延迟,建立了产氢量的半经验模型,如式(56)所示:

(56)

式中:i为电流密度;ai为拟合参数。

2.5.2 储氢罐模型

储氢罐模型是一种描述制氢系统中储存氢气的部件的数学模型,可以用来分析储氢罐的压力、容量、温度等状态变化,以及储氢罐与制氢系统的耦合关系。除了产氢量模型,陈鸿琳等人[32,69,85-86]建立了储氢罐模型,用于观测储氢罐压力。其根据理想气体状态方程计算,具体方法如式(57)所示:

(57)

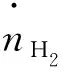
上述文献是从储氢罐压力为目标建立模型,闫庆友等人[62,87]以储氢罐容量变化建模,具体如式(58)所示:

VH(t)=VH(t-1)+Pfg(t)δρα1

(58)

式中:Pfg(t)为发电站输出功率;VH(t)储氢罐容量;α1表示电解槽运行效率;δ为比例系数;ρ表示每kW·h电通过电解槽所能产生的氢气质量。该公式考虑了制氢系统与电解电源的耦合关系,并且假设储气罐内的压力和温度保持恒定。

2.5.3 传质模型

在阴极内,水分解并形成氢气。在阳极内,水和氧气通过膜进行交换。传质过程会影响到气体的浓度、压力、流量等参数,进而影响到电解槽的电压、效率、产氢量等性能指标。为了描述传质过程,可以采用不同的建模方法,根据考虑的空间维度和物理场的复杂程度,可以分为以下几种类型:

1)集总模型。

该模型为常微分方程模型,不考虑电解槽和系统部件内部结构,将电解槽或设备视为一个整体,只考虑其整体的输入输出关系,忽略其内部的空间分布和变化。该模型广泛用于系统级的分析和控制设计,计算量较小,但精度较低。

该模型可以使用质量守恒原理来建立,即认为电解槽内气体摩尔浓度的瞬时变化等于进入和离开电解槽的摩尔流量之差,计算氢气的摩尔浓度的瞬时变化[10,31],如式(59)所示:

(59)

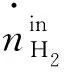
2)分段模型。

该模型考虑电解槽和辅机设备内部结构,将系统划分为若干个单元或段,每个单元或段只考虑其沿着流动方向的变化,忽略其垂直于流动方向的变化。该模型适用于系统的细化分析和优化设计,计算量适中,但精度有限。

该模型可以使用质量守恒和质量传输原理来建立,即认为电解槽内气体摩尔浓度的瞬时变化等于进入和离开该单元或段的摩尔流量之差,以及该单元或段内气体的扩散和反应造成的摩尔流量之和。Zhao D[86,88]等人使用偏微分方程(partial differential equation, PDE)进行传质的更精确求解,在式(59)的基础上添加一个维度,如式(60)所示,方程变为:

(60)

式中:z表示流动方向下的位置变量。

3)高维模型。

该模型考虑电解槽和辅机设备的内部结构,将设备划分为若干个有限元或有限体积,每个有限元或有限体积考虑其在所有空间维度上的变化。该模型适用于电解槽和设备级的分析,常用于电解堆结构和流场设计,计算量较大,但精度较高。可将模型描述为式(61)[88]:

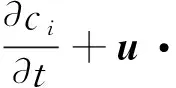
(61)

式中:ci为溶解气体的浓度;Di为扩散系数;Ri为反应项,与产氢量的计算类似,可以用法拉第定律来表示。

上述模型也可以用压力的形式来表达[78,89],可以用来分析渗透性介质中的气体分离、膜过滤、水处理等过程,该模型表明了渗透性流体中的质量传递受到压力驱动和扩散阻碍两个因素的影响。压力驱动使得混合物中所有组分都沿着压力梯度方向流动;扩散阻碍使得混合物中不同组分之间发生相对运动,从而形成浓度差。当压力驱动和扩散阻碍达到平衡时,就形成了稳态传递。模型可以表示为式(62):

(62)

式中:B0为渗透系数,反映了渗透性介质对流体的阻力,值越大,说明流体通过介质的能力越强;yi为摩尔分数;Dieff是混合物中每个组分i的有效扩散率,反映了混合物中各组分之间的扩散能力,值越大,说明组分i的扩散速度越快。

综上,产氢量模型引入了半经验公式,反应动态变化对制氢量的影响;建立了储氢罐模型,其建立过程考虑了储氢罐内部气量的平衡。建模方法遵循了理想气体状态方程等基本原理,能合理描述气路中的产氢和储氢过程,然而仍需注意:产氢量计算中法拉第效率的影响因素仍需研究;储氢罐模型可加入尺寸、阀门、管径等实际特征;可采用压降模型更全面描述气路流动。

实际上,电解制氢系统气路还包含分水器、纯化等部件,管路上的压力,尤其是电解槽附近管路的压力,以及氢氧两侧的压力差也是建模研究的重点,目前文献中尚未有相关模型,是值得后续关注的重点领域。此外,需要加强与电解槽、水路的协同建模。

2.6 模型耦合关系

本文涵盖了多个物理量的PEM电解制氢系统建模,包括电解槽电压模型、膜水合模型,以及系统水、热、电、气模型,这些模型之间存在着复杂的关联关系和耦合效应。系统中的电流、温度、气体压力、水流速等因素会相互影响,从而影响到系统的工作电压、发热功率、产氢速率、储氢压力、能量平衡和效率等性能指标。模型耦合关系如图11所示,主要体现在以下五个方面:

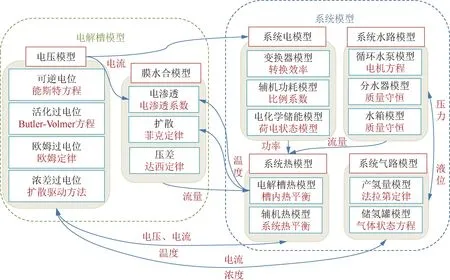
图11 模型耦合关系图Fig.11 Model coupling diagram

1)系统热模型和电压模型之间的耦合,主要体现在温度对电压中可逆电位和各个过电位的影响,以及电流和电压对发热功率的影响。温度升高会降低可逆电位、活化过电位,增加浓差过电位温度升高也会降低膜的电阻,减少欧姆过电位,从而降低了电解槽的工作电压。电流和电压决定了电解槽的发热功率,发热功率又影响了系统的温度分布和变化。

2)系统气路模型和电压模型之间的耦合,主要体现在气体浓度对电压中可逆电位、活化过电位和浓差过电位的影响,以及电流对产氢量和储氢罐压力的影响。气体浓度越高,可逆电位越低,活化过电位越大,浓差过电位越小。因此,气体浓度会影响到工作电压的大小和变化。另一方面,工作电流决定了产氢速率和储氢罐内的氢气压力。储氢罐内的氢气压力又会影响到气路系统中的流动阻力和泄漏损失。

3)膜水合模型和电压模型、热模型之间的耦合,主要体现在电流对电渗透量的影响,以及温度对电渗透系数和扩散系数的影响。膜两侧的水分布不均匀会影响到膜的导电性、离子交换容量、孔隙率等参数,进而影响到欧姆过电位、活化过电位等。另一方面,温度会影响到膜中水分子的扩散系数和迁移系数,从而影响到膜两侧的水分布和输运速率。

4)系统电模型和热模型、膜水合模型之间的耦合,主要体现在辅机功耗对辅机发热量的影响,以及变换器功率、储能功率对发热功率的影响。辅机功耗会转化为发热量,影响到系统的温度分布和变化。变换器和储能的功率会影响到系统的能量平衡和效率。

5)系统水路模型和热模型、气路模型之间的耦合,主要体现在循环水流量对散热量的影响,以及液位和压力对水路流量的影响。循环水流量越大,散热量越大,系统温度越低。液位和压力会影响到水路系统中的流动阻力和泵阀特性,从而影响到水路流量的大小和变化。

这些耦合效应和关联关系在整个PEM电解制氢系统中相互作用,需要综合考虑和建模,以更全面地描述系统各个物理量之间的相互影响,从而深入理解系统的行为,准确评估系统的性能。

3 亟需解决关键问题

深入梳理国内外现有研究工作,目前还存在问题亟需解决。具体如下:

在PEM电解制氢建模方面,由于和燃料电池作用机理相反,很多模型都是直接使用或借鉴燃料电池的方法,忽视了内在机理的研究,加大PEM电解制氢运行机理的研究可以有效解决催化剂活性、电流电压特性动态衰减、氢渗等问题,是未来研究的热点。要建立更准确的微观模型,加强理论计算和表征测试的研究。

在PEM电解制氢模型验证方面,PEM电解制氢模型所涉及的参数过多,一方面很多参数在实际工作中不具备测试的条件,另一方面很多理想状态下的参数无法测得,使得只能借鉴其他文献支撑,不能很好与试验结果相对应。因此,借助参数辨识、统计分析、智能算法等优化系统模型准确性,是未来的研究方向。需要进一步开发参数精确识别与优化方法,提高模型预测精度,也需要收集更丰富的实验数据以供模型验证。

在PEM电解制氢系统方面,由于PEM制氢系统研究起步较晚,在系统方面研究的文章较少。首先,系统辅机模型少,如纯化、管道、阀门等,使得电解制氢系统模型与实际结果存在偏差。需要扩展PEM电解制氢系统模型的边界,加入更多子系统与部件,构建全面反映系统特征的模型,并加强对不同部件的协同建模。其次,动态控制方法少,很多环节做了简化,不能够全面反映PEM电解制氢宽范围波动适应性的特点。开发动态控制模型,考虑PEM系统的适应性,为其高效稳定运行提供支持,加强对系统动态特性的研究。最后,绿氢的制备需要PEM电解制氢系统与风/光可再生能源结合,但是现在可再生能源-PEM制氢模型较少,不能够反映风/光可再生能源与PEM电解制氢系统耦合协调的问题。加强对可再生能源与PEM电解系统的耦合模型研究,实现对绿氢全过程的预测,需要真实运行数据进行验证。PEM电解制氢系统模型的建立是未来的研究重点。

4 结 论

本文综述了近年发展起来的PEM电解制氢系统模型,阐述了PEM电解槽的技术基本原理,结合电化学、流体力学、传质传热学等基本理论,参考国内外文献资料对PEM电解制氢系统建模方法,从电解槽到系统,在水、热、电、气四个方面综述了PEM制氢全系统模型。目前PEM电解水制氢系统建模是热点,尤其在电解槽模型方面研究众多,但是还存在不足:1)电解堆模型和耐久性建立关系少,比如催化剂活性面积、电压电流特性是动态衰减的,计及耐久性的建模值得研究;2)模型的准确性,需要和试验结合,借助参数辨识、智能算法等优化系统模型;3)系统辅机模型少,很少涉及纯化、管道、阀门等部件,尤其是动态的,用于控制的模型很少,很多环节做了简化,结合泵阀的机电调节特性,建立全系统动态模型很有必要。

综上,需要加强PEM电解槽及辅机模型设计研究,建立统一建模框架,强化参数优化与耦合分析,搭建更为精准、全面的PEM电解水制氢系统模型,掌握动/静态PEM电解水制氢系统建模方法,支撑PEM电解槽及制氢系统的研发与示范工程推广。本文旨在通过对PEM电解制氢系统建模方法的综述,帮助读者全面了解该系统的动态和静态特性,选择适用的建模策略,为PEM电解制氢系统的设计、运行和控制优化提供理论支撑。