基于HPM视角的概率论与数理统计课程思政探究*
——以正态分布为例
2024-01-31杨晓航
杨晓航
(河南工学院 理学部,河南 新乡 453003)
0 引言
概率论与数理统计是研究和揭示随机现象统计规律性的一门数学课程,旨在培养学生的概率思维和统计分析能力。概率论主要研究随机现象及统计规律性的数量关系,而数理统计以概率论为基础,研究如何有效地收集、整理和分析随机数据,并做出统计推断。概率论与数理统计是当前很多重要的学科如金融学、信息学、人工智能等的基础,其与生活实际关系紧密,有极高的应用价值[1]。基于数学史与数学教育(History and Pedagogy of Mathematics,HPM)视角,在课堂上融入学科发展的历史与成就,有利于与课程思政有机融合,将传授知识、培养能力和塑造价值三者融为一体,将教学引向更高的层次[2]。
正态分布是一个在数学、物理等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力。在进行正态分布教学时可深挖其发展史料,这有利于学生深刻理解概率思想的形成过程,化解他们对于正态分布概率密度函数的畏难情绪;有助于激发学生的学习兴趣,促进学生的人格养成,实现知识传授和价值引领的统一,贯彻落实立德树人的根本任务[3]。
1 教学背景
正态分布在概率论与数理统计中的地位十分特殊,在学习了离散型随机变量之后,正态分布作为最重要的连续型随机变量,既是对前面内容的补充,又是后续学习统计推断和假设检验的基础。正态分布是由二项分布发展而来的,这一发展过程主要得益于数学家们对中心极限定理和误差分析的研究。中心极限定理的主要推动者是拉普拉斯,他的研究对概率论领域产生了深远影响。而误差分析的主要推动者则是高斯,他的研究主要集中在数理统计领域。正态分布的教学重点是正态分布概率密度曲线的特点和性质,难点是利用正态分布解决生活实际问题。
概率密度函数概念十分抽象,教材一般都未说明其是通过什么原理推导出来的,学生无法将其和前置知识建立联系,也无法体会正态分布在生活实际中的应用价值,在学习时极易产生畏难情绪。基于HPM视角,教师应预见学生的认知发展,在教学中融入正态分布的发展历史,让学生切身体会概念的形成过程[3]。
2 教学思路
在学习正态分布概率密度曲线前,学生已经学习了包括两点分别、二项分布和泊松分布在内的离散型随机变量以及均匀分布、指数分布两种连续型随机变量,并且在高中阶段对正态分布有了一定了解。在此基础之上,可基于HPM视角引出两条线索,其一是通过棣莫弗(Abraham de Moivre)的故事介绍二项概率逼近,其二是通过高斯(Gauss)的故事介绍误差分析,两条线索都可导出正态分布,引导学生体会知识形成的过程[4]。教师可先通过GeoGebra软件帮助学生直观认识正态分布密度曲线及两个参数对曲线的影响,进而讲解标准正态分布及Φ(x)函数表的查用,最后突破难点3σ准则及正态分布在生活中的应用。
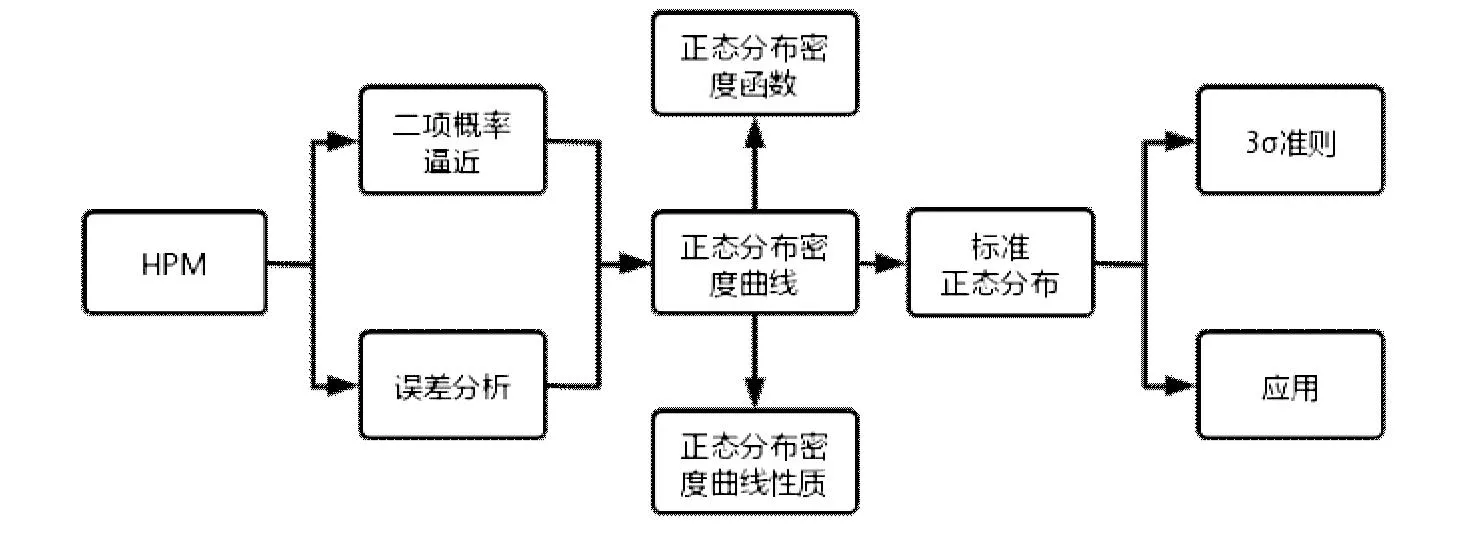
图1 教学流程图
3 教学设计
3.1 引入历史,激发兴趣(附加式)
教师可采用附加式引入数学史的方法,在正式上课之前通过超星学习通平台向学生推送分组学习任务:探寻德国10马克钞票正面图案(图2)背后的故事,并在课堂上相互分享。

图2 德国1993年版10马克钞票正面
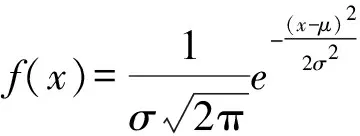
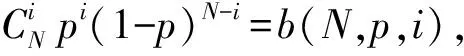
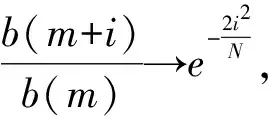
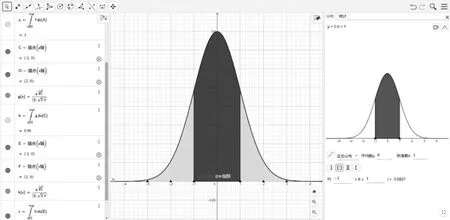
-∞ 正态分布的概率密度函数在上述的积分公式中出现了,二项分布的极限分布便是正态分布,同时,也为统计学史上占据重要地位的中心极限定理奠定了基础。附加式数学史的融入重演了正态分布的发现过程,可使学生认识到了正态分布在概率论与数理统计中的地位,对正态分布概念的形成有了整体的印象,也消除了学生的畏难情绪。 图3 高尔顿板 此时可以采用复制式的方法将数学史融入教学,即引导学生解决高尔顿板问题,深化学生对连续型随机变量概率密度函数的理解及正态分布的理解。可以通过以下三个问题进行引导: (1)高尔顿板最直接推出的是二项分布,而不是正态分布,那它是如何趋于正态分布的? (2)从二项分布到正态分布,主要问题是估计阶乘,能否参考附加式引入中介绍的棣莫弗的方法使用斯特林公式解决? (3)这个数学问题的解决使你对正态分布有了哪些不一样的认识? 在高尔顿板实验中,小球每随机自由下落一层都有向左或向右的可能,小球最终的落点受到一些因素的左右。类似地,在自然界中许多随机现象都受到各种干扰因素的影响,这些因素会影响事件的分布。然而,在这些干扰因素叠加的情况下,只要样本数量足够大,这些随机现象通常会遵循正态分布规律。教师重视数学知识的形成过程,引导学生追寻数学知识产生的思维轨迹,就更能他们感受数学之美,培养他们的数学精神。 学生已经加在高中阶段掌握了正态分布概率密度函数的性质,大学课堂上教师可以使用Geogebra软件画出正态分布概率密度图像(如图4),并分别设置参数μ和σ的滑动条,通过动态演示直观展示两个参数值的改变对图形的下影响: 图4 正态分布概率密度图像 (1)曲线关于x=μ对称,当固定σ,改变μ的值,图形沿着Ox轴平移,而不改变形状。 此时,教师可以给出一个例题,建议选择身高、体重、成绩等与学生生活关系紧密的问题,突出正态分布应用价值的体现,例如。 公共汽车是人们日常出行经常使用的交通工具,请同学们帮忙设计公共汽车车门的高度,要求成年男性在上下车时与车门顶头碰头机会在小于0.01以下。设男子身高X∶N(170,62),车门的高度应如何确定? 借由此类例子引出3σ准则,教师可用GeoGebra软件绘制标准正态分布函数(如图5),输入对应区间求得具体概率及填充颜色,向学生展示当X∶N(0,1)时,P{-1≤X≤1}=68.26%,P{-2≤X≤2}=95.44%,P{-3≤X≤3}=99.74%。 图5 3σ准则 当X∶N(μ,σ2)时,仍然有P{μ-σ≤X≤μ+σ}=68.26%,P{μ-2σ≤X≤μ+2σ}=95.44%,P{μ-3σ≤X≤μ+3σ}=99.74%,随机变量X落在(μ-3σ,μ+3σ)内几乎是肯定的事。 正态分布概率密度函数及分布函数看起来是非常复杂的,但它不是为了定义而定义,是为了解决我们生活中实际遇到的问题而定义的[7]。数学史上还有许许多多和正态分布相似的定理,它们的发现往往历经艰辛,需要几代数学家的努力,而当学生直面一个严谨而抽象的定理时,教师应结合数学史将定理的形成过程展现给学生。这样既可以让学生系统而全面的接受知识,又可以促进学生数学思维的形成。学生意识到知识的形成是如此不易,会在被数学家百折不挠、不断探索的精神感染下,激发出对数学学习的热情。3.2 正态分布的发展(复制式)
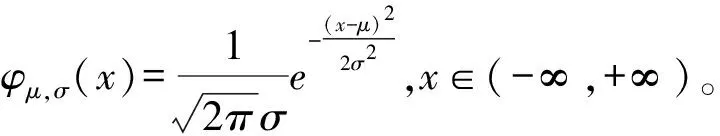
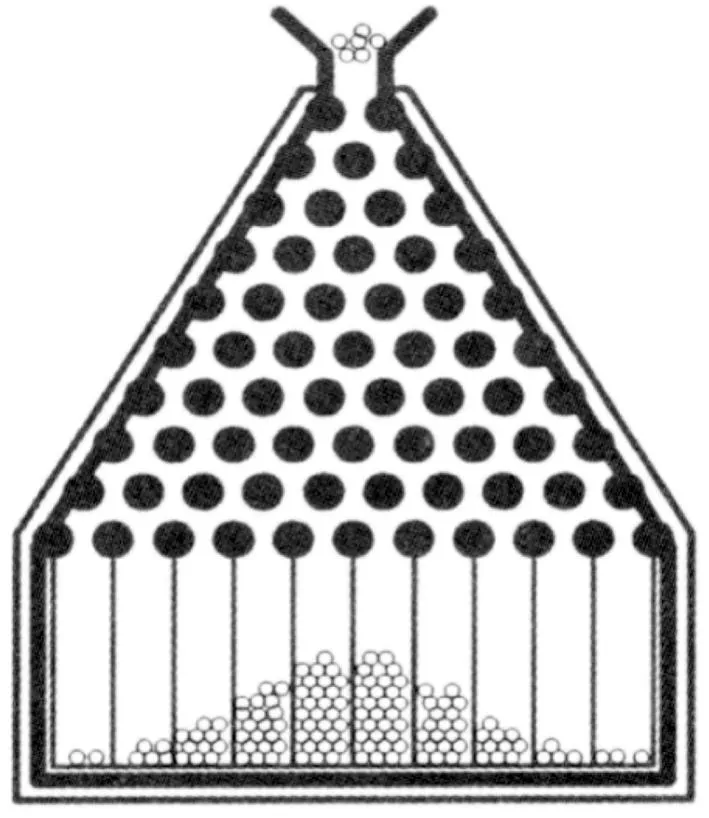
3.3 依据现实情境,深入理解
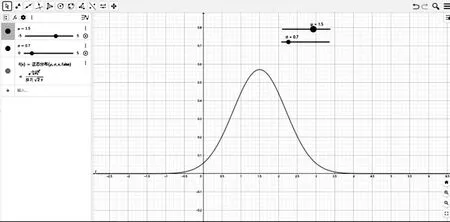
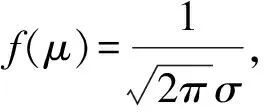
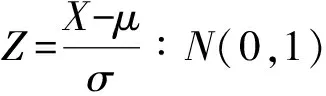
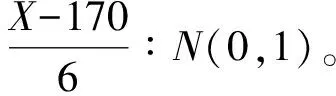
4 小结
