预应力混凝土矮塔斜拉桥敏感性参数分析
2024-01-30刘松鑫徐海宾
刘松鑫, 徐海宾, 李 磊
(1.河南理工大学土木工程学院 河南 焦作 454000;2.河南省交通规划设计研究院股份有限公司 河南 郑州 450000)
0 引言
矮塔斜拉桥是由索塔、主梁以及斜拉索组成的超静定结构体系,受力性能介于梁式桥和传统斜拉桥之间,具有造型美观、结构刚度大、造价低、施工方便等特点,近几年在城市道路、景观桥梁、高速铁路中得到广泛应用[1]。矮塔斜拉桥在实际施工过程中会受到很多因素的影响,导致实际成桥状态和设计目标存在误差,我们把这个些影响因素称之为参数,主要包括两个方面:结构布置参数和构件状态参数[2],因此需要对矮塔斜拉桥的这些参数进行分析,通过识别出敏感性参数,在施工过程中加以控制,以减小对成桥状态的不利影响。
刘昊苏等[3]对矮塔斜拉桥索塔刚度、主梁刚度及斜拉索刚度进行了敏感性分析,并对三者的敏感性进行排序。徐佰顺等[4]分析了主梁自重、主梁弹性模量、斜拉索索力、预应力张拉力、混凝土收缩徐变和体系温度参数变化下主梁的应力和挠度的变化规律,判别出对应力和挠度的敏感性参数和非敏感性参数。王灿等[5]分析了温度变化、结构自重、施工索力、主梁刚度等参数在成桥阶段对桥梁内力、线形及索力的影响规律。邬晓光等[6]分析了结构重度、拉索弹性模量、拉索初张力、整体温度等参数变化的影响规律。冯仲仁等[7]研究了主梁自重、斜拉索弹性模量、施工荷载、初张拉力、温度的变化对主梁线形、应力和索力的影响。张亚海等[8]研究了拉索弹性模量、主梁重度、主梁刚度及索塔刚度等设计参数对全桥线形、内力的影响。刘增武等[9]研究了主梁自重、斜拉索刚度、施工荷载、斜拉索初张拉力、混凝土收缩徐变等参数变化对索塔应力和偏位,以及主梁线形和索力的影响规律。鲍英基等[10]分析了拉索索力、预应力、桥面铺装层厚度和混凝土徐变系数参数的敏感性,对矮塔斜拉桥主梁的应力和位移的影响。
本文通过控制变量法,研究了主梁自重、主梁混凝土弹性模量、预应力张拉力3个结构状态参数对矮塔斜拉桥成桥状态的敏感性,分析出在施工过程中对成桥状态影响最大的参数。
1 计算模型
1.1 工程概况
柬埔寨Norea大桥为双塔单索面预应力混凝土矮塔斜拉桥,结构体系为塔梁固结,墩梁分离的支座体系。跨径布置为(108 m+180 m+108 m),边中跨比为0.6。桥面以上索塔总高为60 m,其中装饰性索塔塔冠高11 m,高跨比为1/3。斜拉索为单索面(水平双排索,间距1.2 m)、扇形布置,每个塔上设有32根斜拉索,全桥共64根。斜拉索在主梁上纵向间距为4.2 m,塔上竖向间距为1.5 m。斜拉索在塔上连续通过鞍座两侧对称锚于主梁两道中腹板顶部。箱梁采用单箱三室断面,跨中梁高3.2 m,支点梁高6.0 m。跨中52.4 m采用3.2 m等高梁,以便于施工。中墩支点左右各3 m(共计6 m)长度范围采用6.0 m梁高,支点梁高采用二次抛物线渐变至3.2 m等高段,渐变段长度为60.8 m。中腹板采用直腹板,边腹板采用斜腹板,以满足受力和景观要求。主桥布置如图1所示。
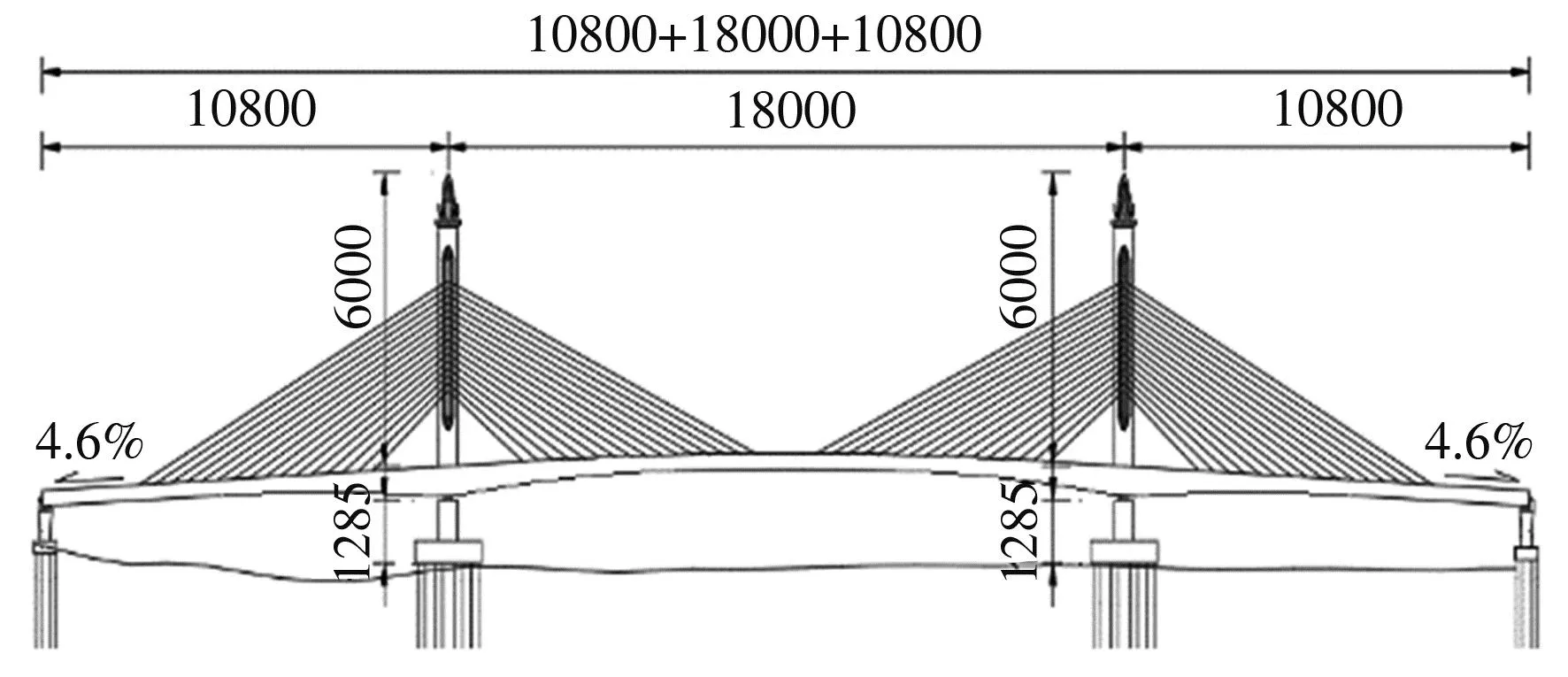
图1 矮塔斜拉桥总体布置图 (单位:cm)
1.2 有限元模型
采用有限元软件Midas Civil 2021建立全桥的空间有限元计算模型,全桥共划分560个节点,467个单元,其中梁单元339个,桁架单元128个。全桥有限元模型如图2所示。
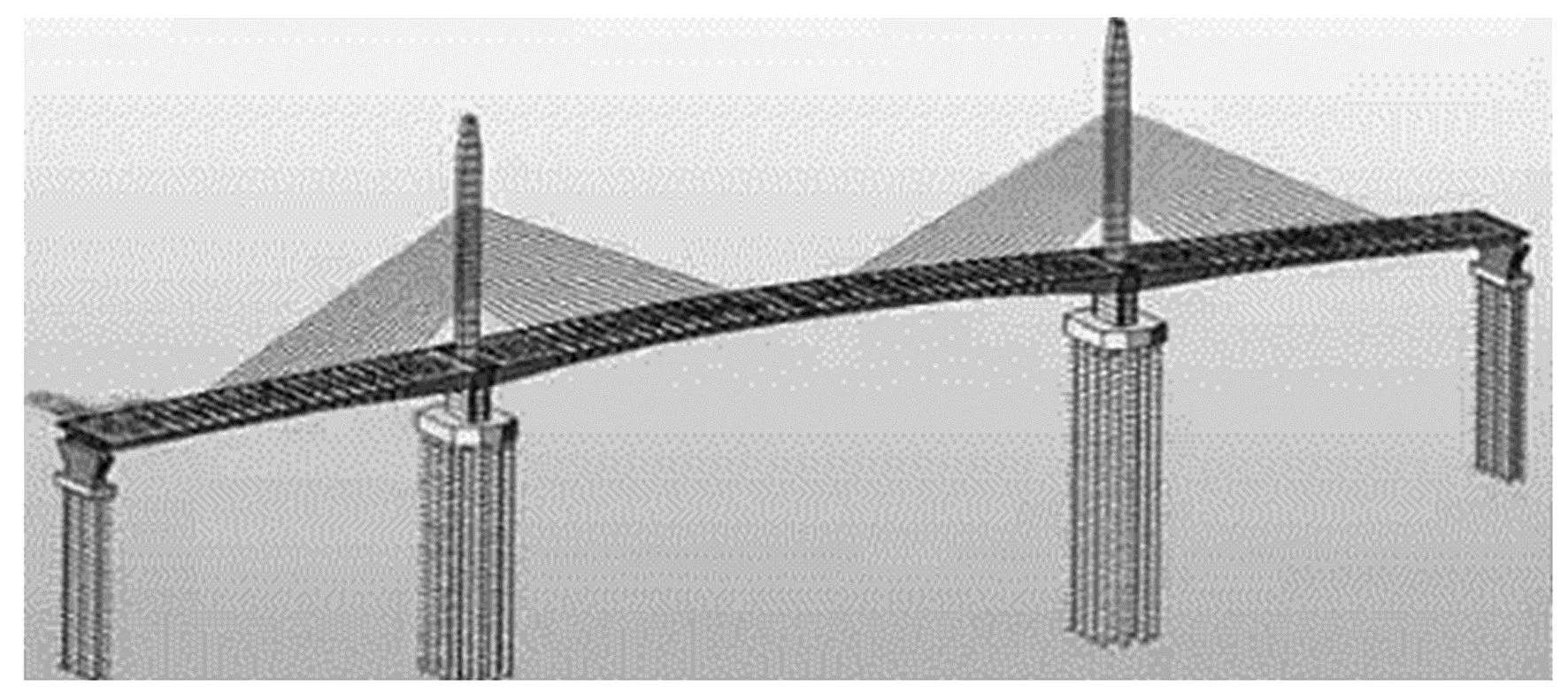
图2 矮塔斜拉桥有限元模型
有限元模型中材料参数如表1所示。

表1 材料参数表
2 参数敏感性分析
本文主要对主梁自重、主梁混凝土弹性模量、预应力张拉力3个结构状态参数进行敏感性分析。通过选取控制参数在设计值上的4种变化情况,分析对斜拉索索力、主梁弯矩、主梁竖向位移的影响,当一个参数变化时,其他参数保持设计值不变,研究参数及控制变化范围(如表2所示)。(图中数据增量以负弯矩为正,以位移向下为正)。

表2 参数状态表
2.1 主梁自重影响分析
在施工过程中,主梁混凝土的容重误差会导致主梁自重产生一定的误差。因此在有限元软件建模分析的过程中,通常改变主梁容重,来进行参数敏感性的分析。Norea矮塔斜拉桥混凝土设计容重为26 kN/m3。分别分析在这4种工况下混凝土自重对全桥结构受力状态的影响
2.1.1 主梁自重对成桥索力的影响
通过改变主梁自重分析对成桥索力的影响,计算结果见图3所示 。

图3 主梁自重改变±3%和±5%索力增量
由图3可以看出来,成桥索力随着主梁自重的变化而变化,增减的幅度和自重的变化成正相关,成桥索力变化幅度最大的是中部斜拉索,自重增减5%时,斜拉索索力分别增减3.21%和2.72%,因此由分析可知主梁自重改变会对成桥索力产生影响。
2.1.2 主梁自重对主梁弯矩的影响
通过改变主梁自重分析对主梁弯矩的影响,计算结果如图4所示。
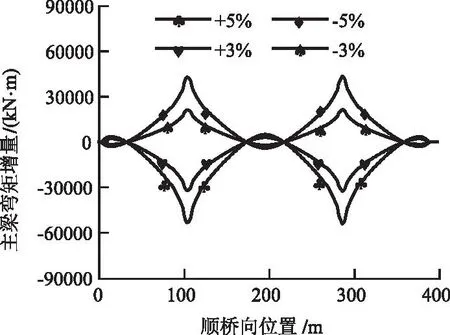
图4 主梁自重改变±3%和±5%弯矩增量
由图4可以看出来,当主梁自重发生改变时,索塔处弯矩变化最大,当主梁自重增加3%和5%时,主塔处负弯矩分别增加12.17%和18.76%,当主梁自重减少3%和5%时,主塔处负弯矩分别减少11.23%和22.89%。由此分析可知,主梁自重改变会对主梁弯矩产生较大的影响,主要原因是主梁自重改变影响了桥梁恒荷载及斜拉索索力的变化,从而导致主梁弯矩变化明显,因此在施工过程中要严格控制混凝土配合比和模板的精度,减小由于主梁自重改变对结构受力的影响。
2.1.3 主梁自重对主梁竖向位移的影响
通过改变主梁自重分析对主梁竖向位移的影响,计算结果见图5所示。

图5 主梁自重改变±3%和±5%位移增量
由图5可以看出来,当主梁自重发生改变时,主梁最大位移变化量出现在跨中位置及边跨合拢段,当主梁自重增加5%时,主梁位移变化量最大,最大值为22.55 mm,增幅为18.79%。由此分析可知,主梁自重改变也会对位移产生较大的影响,主要原因还是主梁自重改变导致恒荷载变化,从而影响主梁线性。
综上所述,当主梁自重变化时,对斜拉索索力、主梁弯矩和竖向位移影响较大,因此主梁自重属于敏感性参数。
2.2 主梁弹性模量影响分析
Norea矮塔斜拉桥主梁弹性模量为3.6×104MPa。分析分别在这4种工况下主梁弹性模量对全桥结构受力状态的影响。
2.2.1 主梁弹性模量对成桥索力的影响
通过改变主梁弹性模量分析对成桥索力的影响,计算结果见图6所示。
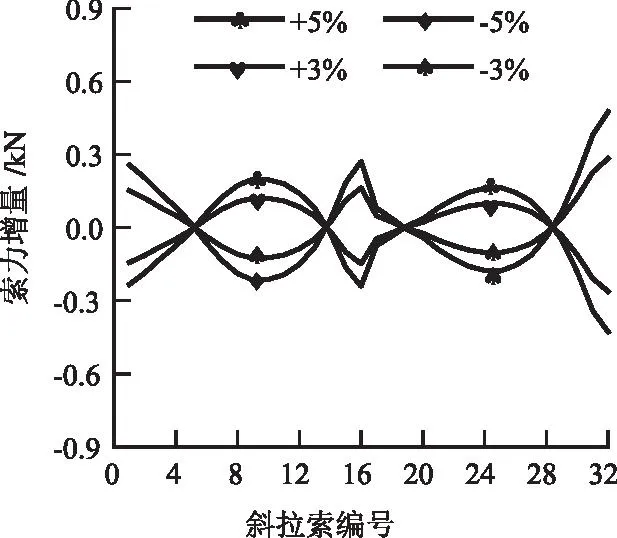
图6 主梁弹性模量改变±3%和±5%索力增量
由图6可以看出来,在4种工况下下,主梁弹性模量变化时,斜拉索索力变化并不明显,变化值最大不超过1 kN,可以忽略不计,因此主梁弹性模量为非敏感性参数。
2.2.2 主梁弹性模量对主梁弯矩的影响
通过改变主梁弹性模量分析对主梁弯矩的影响,计算结果见图7所示。

图7 主梁弹性模量改变±3%和±5%弯矩增量
由图7可以看出来,当主梁弹性模量改变时,主要影响桥塔周围弯矩,变化最大的工况是当主梁混凝土弹性模量减少5%时,桥塔位置处负弯矩增加515.21 kN·m,但增加幅度仅为0.22%。因此主梁弯矩对主梁弹性模量的变化不敏感。
2.2.3 主梁弹性模量对主梁竖向位移的影响
通过改变主梁弹性模量分析对主梁竖向位移的影响,计算结果见图8所示。
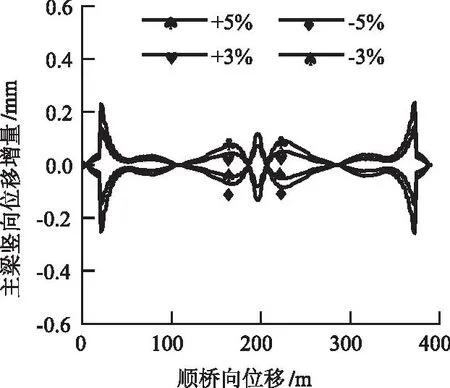
图8 主梁弹性模量改变±3%和±5%位移增量
由图8可以看出来,当主梁弹性模量在设计值上变化+5%和-5%时,主梁位移变化量在-0.25~0.23 mm之间,变化幅度最大为0.21%,主梁竖向位移变化幅度不超1 mm。由此分析可知,主梁混凝土弹性模量改变对于主梁位移的影响基本可以忽略,主梁位移对主梁混凝土弹性模量的变化不敏感。
综上分析可知,主梁弹性模量的变化对主梁的内力和线性的影响并不显著,属于非敏感性参数。
2.3 预应力张拉力影响分析
在施工过程中,各种因素会导致预应力损失,因此通过改变预应力张拉力来研究对矮塔斜拉桥的内力和位移产生的影响。Norea矮塔斜拉桥设计预应力张拉力为1395 MPa。分析分别在这4种工况下预应力张拉力对全桥结构受力状态的影响。
2.3.1 预应力张拉力对成桥索力的影响
通过改变预应力张拉力分析对成桥索力的影响,计算结果见图9所示。

图9 预应力张拉力改变±3%和±5%索力增量
由图9可以看出来,预应力张拉力发生改变时,斜拉索索力值都均匀发生变化,最大增量为当预应力张拉值减少5%时,成桥索力值增加了28.76 kN,增幅为1.09%。由此分析可知,斜拉索作为体外预应力筋和主梁内预应力钢筋相互配合,共同作用来分担主梁的各种荷载,当预应力张拉力增大时,相应的斜拉索的索力值会减小。因此斜拉索索力对预应力张拉值的改变非常敏感。
2.3.2 预应力张拉力对主梁弯矩的影响
通过改变预应力张拉力分析其对主梁弯矩的影响,计算结果见图10所示。

图10 预应力张拉力改变±3%和±5%弯矩增量
由图10可以看出来,预应力张拉力发生改变时,主梁弯矩相对变化较大,尤其在桥塔位置出负弯矩变化最大,且当预应力张拉力减少5%时,主梁负弯矩最大增量为1.84×104kN·m,增幅为88.01%。由此分析可知,预应力张拉力变化时对主梁弯矩值影响较大,属于敏感性参数。
2.3.3 预应力张拉力对主梁竖向位移的影响
通过改变预应力张拉力分析其对主梁竖向位移的影响,计算结果见图11所示。

图11 预应力张拉力改变±3%和±5%位移增量
由图11可以看出来,预应力张拉力发生改变对主梁竖向位移影响显著,主梁竖向位移发生改变主要在跨中位置和边跨和龙段处,当预应力张拉力减少5%时,主梁竖向位移最大增加量为7.39 mm,增幅为29.30%。由此分析可知,预应力张拉力的改变影响结构受力状态,从而导致主梁竖向位移增大,因此预应力张拉力属于敏感性参数。
综上分析可知,桥梁结构中的预应力钢筋作为主要的受力构件,预应力张拉力的变化会导致结构的内力和线性出现较大的改变,且对斜拉索的索力影响较为显著,因此预应力张拉力属于敏感性参数。
3 结论
本文以柬埔寨 Norea 三跨(108 m+180 m+108 m)双塔单索面预应力混凝土矮塔斜拉桥为研究对象,建立了空间杆系有限元模型,分析了主梁自重、主梁弹性模量、预应力张拉力3个参数变化对成桥状态斜拉索索力、主梁弯矩和竖向位移的影响,得出结论如下:
(1)主梁自重和预应力张拉力对成桥状态影响大,属于敏感性参数。主梁弹性模量对成桥状态影响小,属于非敏感性参数。
(2)通过对3个参数的斜拉索索力、主梁弯矩和竖向位移在4种工况下的分析,3个参数的改变量对斜拉索索力、主梁弯矩和竖向位移的影响成正相关。
