基于多维空间面板决策模型的区域韧性评估研究
——以中原城市群核心区为例
2024-01-30赵子珺
赵子珺
(澳大利亚新南威尔士大学 悉尼 2770)
0 引言
为缩小地区差异,加快区域协同发展,国家提出加快城市群建设,而城市群作为自然-社会-经济复合系统,对推动区域协调发展具有重要作用[1]。我国在2021年将“韧性城市”列入十四五发展规划,“党的二十大”又提出“打造宜居、韧性、智慧城市”,并于2022年5月出台了《安全韧性城市评价指南》,提出加强城市建设、治理,提高风险抵御及恢复能力,韧性研究成为当前主流。“韧性”概念来源于工程领域,关注点集中在抵抗力和恢复力方面[2],但多为单一城市研究,忽略了区域对其造成的影响[3]。特别是2021年郑州市强降雨使中原城市群多数城市受到影响,灾害连锁效应及综合性影响的增强,使单一韧性城市建设无法解决城市问题,也使区域韧性重要性受到广泛关注。区域是个体、组织、网络等形成的集合,区域韧性是将区域作为整体系统进行研究,从系统层面释放韧性能力应对外部冲击和挑战[4],是区域动态适应不同阶段风险和挑战的新研究范式[5],是区域面对短期冲击和长期变化时的自我转型和协调[6],涉及多主体、多客体及多维度内容。2009年,REED 等从单要素层面进行韧性框架构建,并用于基础设施韧性评估中[7];2019年,NYSTRÖM 等将系统内因机制、多重反馈结合进行韧性研究[8];段怡嫣从系统功能出发,对社会生态、网络联系等展开研究,为区域韧性研究奠定基础[9];2022年,郭文韬等提出韧性建设时应加强多个问题的综合研究[10]。随着韧性研究扩展,学者们更加关注系统在受到内外部环境影响时的抵抗力、适应力、恢复力及学习力变化情况[11]。目前韧性研究主要集中在京津冀、哈长、东北地区[12-14]及部分省市[15-17],中原城市群作为国家十大城市群之一,核心发展区人口数量较多且与其他城市群发展差距较大,为了对中原城市群核心发展区韧性评估,明确其存在问题及造成区域韧性不高的原因,研究中利用不同时段空间面板数据,从“经济结构、社会、生态、基础设施、区域建设、区域治理”层面建立“抵抗力、适应力、恢复力、学习力”的多维度区域韧性评估决策模型,并引入“投入-产出”模型,将其进行改进,提出区域韧性测算方法,并利用空间杜宾模型对中原城市群核心发展区韧性多维多要素空间分异性测算,明确各维度要素对区域韧性的决定性影响,以实现区域韧性综合提升。
1 区域韧性评估的决策模型构建
1.1 决策模型构建
韧性作为复杂系统概念,不仅表现在内部要素联系上,也表现在面对外部干扰时的应变能力及潜力,也体现在不同能力的相互协同及综合提升[18]。韧性评估不仅包括灾前各项建设及灾害抵抗力的提升和培养,也包括灾前应急演练和管理,及灾害时的适应力和恢复力,并包括灾后内部改善及经验总结、学习等。区域作为完整系统,由多个城市组成,区域内部各城市之间具有较强的联系性,灾害的高连锁效应及综合性影响,使传统以单一灾种及单一要素为主的城市韧性测算方法及模型构建无法满足区域韧性评估需求,需从系统层面出发,综合考虑多要素之间的协同及联系[19]。区域韧性不仅表现在人员、设施和管理安全方面,也体现在生态环境、社会交往及基础设施建设层面,通过每个层面不同要素之间联系,形成区域的抵抗力、恢复力、适应力及学习力[20]。
在区域韧性评估指标构建时,从“经济结构、社会、生态环境、基础设施、社会治理、区域建设”等层面出发,对“抵抗力、适应力、恢复力和学习力”4个维度分析,实现多元要素与多维度内容的结合。在区域发展不同时段,由于内部环境变化及城市建设发展,其抵抗力、适应力、恢复力和学习力对区域韧性影响也各不相同,使区域韧性整体水平随时间呈“S”形上升。为准确表述区域韧性及各要素关系,构建基于时间变化的“抵抗力——适应力——恢复力——学习力多维度空间面板决策模型”,对区域韧性预测。在模型构建时,根据系统要素关系,各维度空间要素相互连接形成某一时期区域韧性。在模型中,o点代表某一时刻区域韧性水平,oa为抵抗力,ob为适应力,oc为恢复力,od为学习力,沿o点轨迹形成区域韧性曲线,区域韧性随时间变化得出区域韧性水平(如图1)。
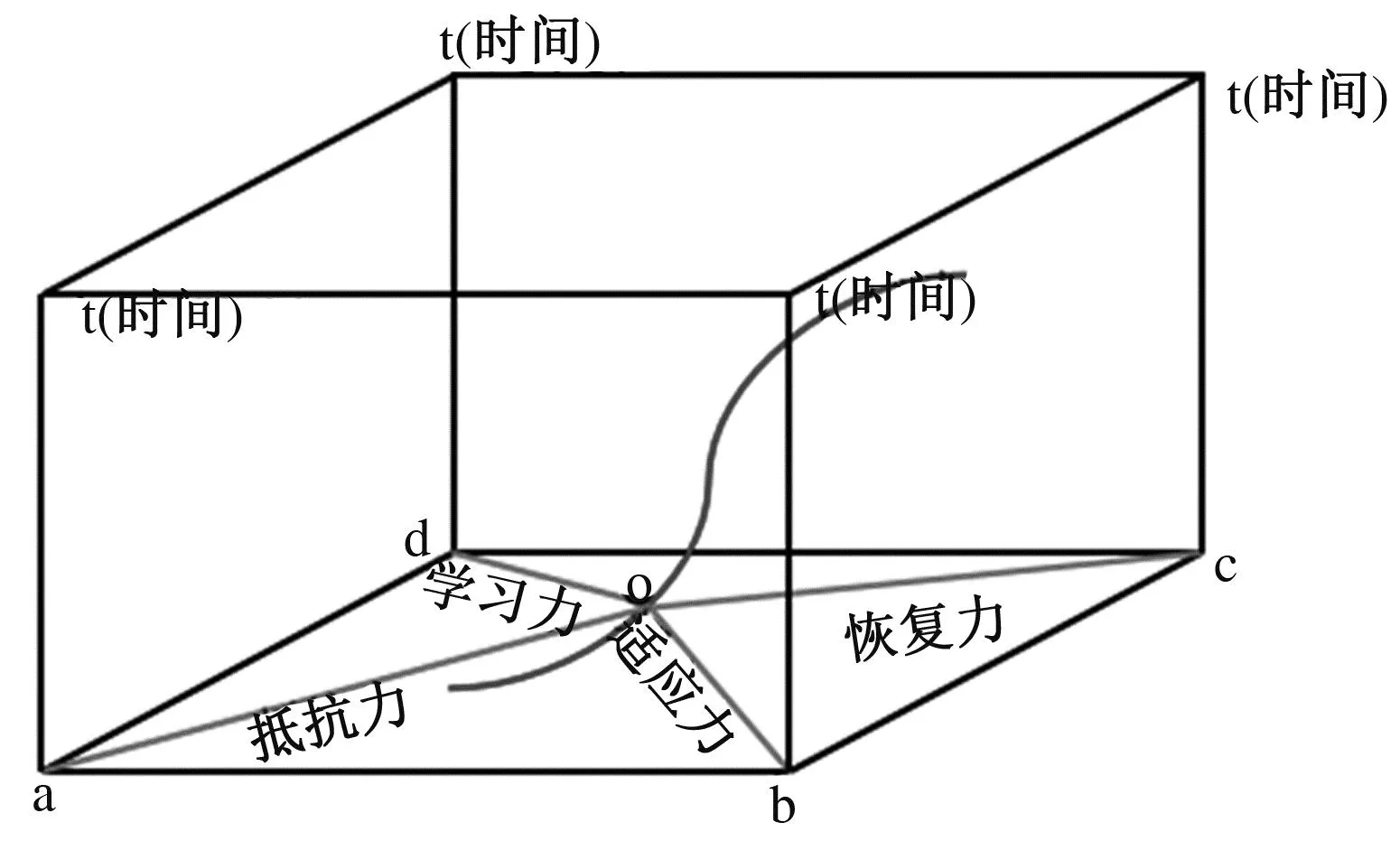
图1 “抵抗力—适应力—恢复力—学习力”多维空间面板决策模型
1.2 区域韧性评估模型多元指标体系构建及权重测算方法
1.2.1 区域韧性评估模型多元指标体系构建
根据“多维空间面板决策模型”及灾害应对要素,参考国内外相关研究[21-22],同时依据韧性系统与各层面耦合关系,形成“1个一级指标、6个二级指标、24个三级指标、32个属性指标”的区域韧性评价指标体系(见图2)。

图2 区域韧性评估多元指标体系构建图
1.2.2 区域韧性评估指标权重测算方法
为了进行区域韧性评估,利用主成分分析法对所有韧性评估因子权重计算。在各因子权重确定时,首先根据各指标和因子建立多个特征向量矩阵,然后利用matlab软件进行权重值计算,获得较为合理的权重系数。
(1)因素和因子权重计算
在对各因素和因子指标权重计算时,利用matlab软件建立特征向量矩阵,对其相似性判断和测算结构验证,确定各因子权重值。
(2)二级指标权重计算
二级指标主要包括经济结构韧性、社会韧性、生态环境韧性、基础设施韧性、区域建设韧性和区域治理韧性,建立五个维度的特征向量矩阵,利用matlab软件确定二级指标权重。
(3)三级及属性指标权重计算
根据上述方法,对每个三级指标权重值计算时,根据三级指标细分,首先对每一构成要素单独计算;然后再计算综合权重值。利用与二、三级指标相同计算方法,对属性指标权重值计算。
2 区域韧性评估测算方法
2.1 区域韧性评估的“多维空间面板决策模型”测算方法
2.1.1 单一城市单一要素韧性测算方法
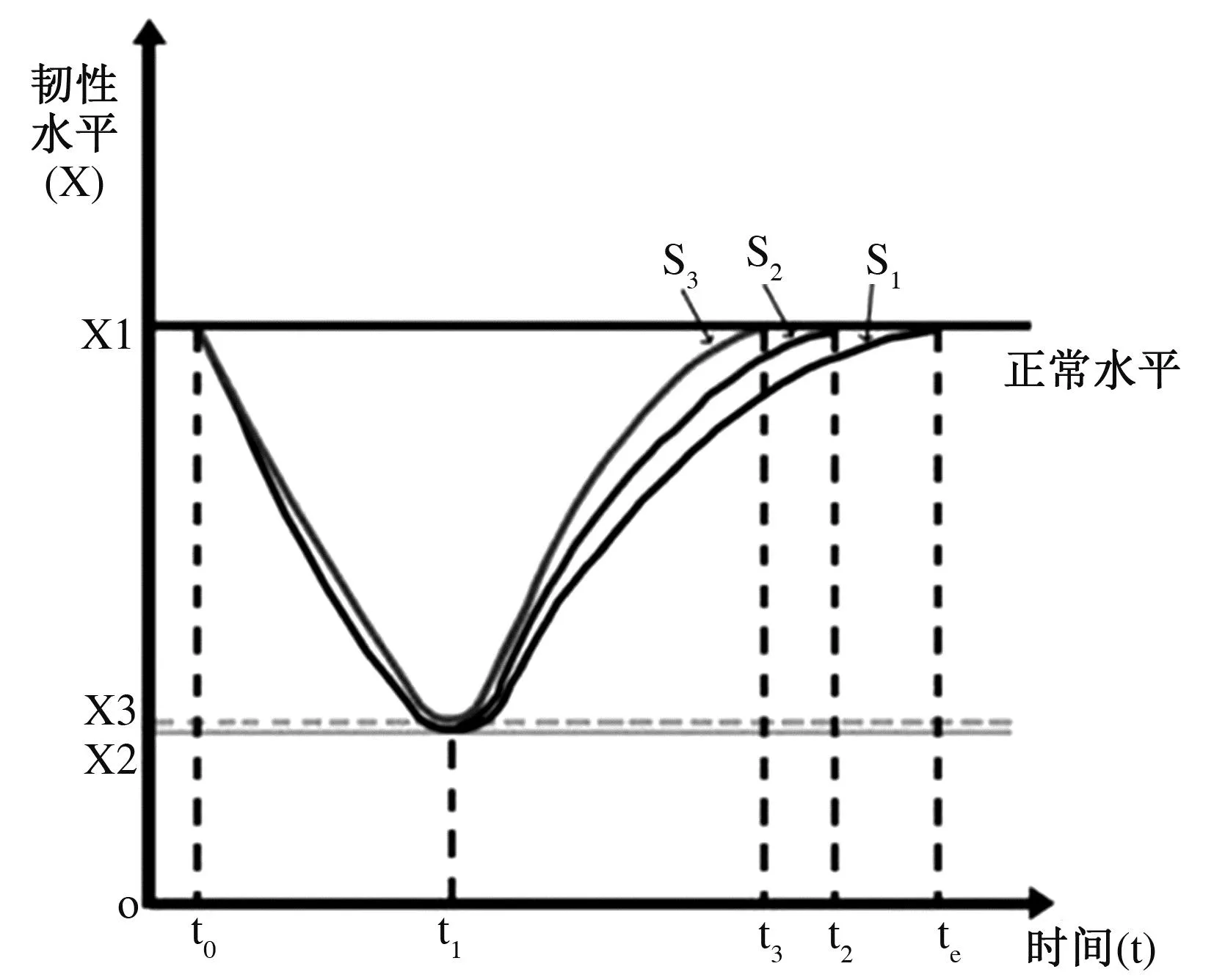
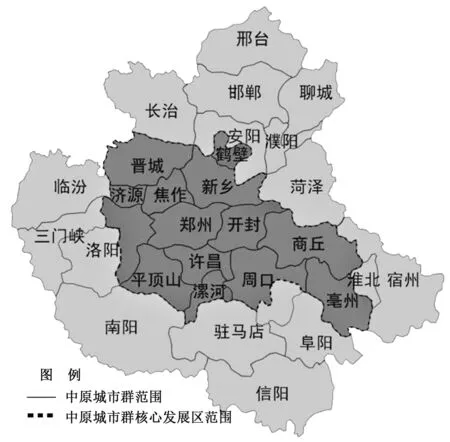
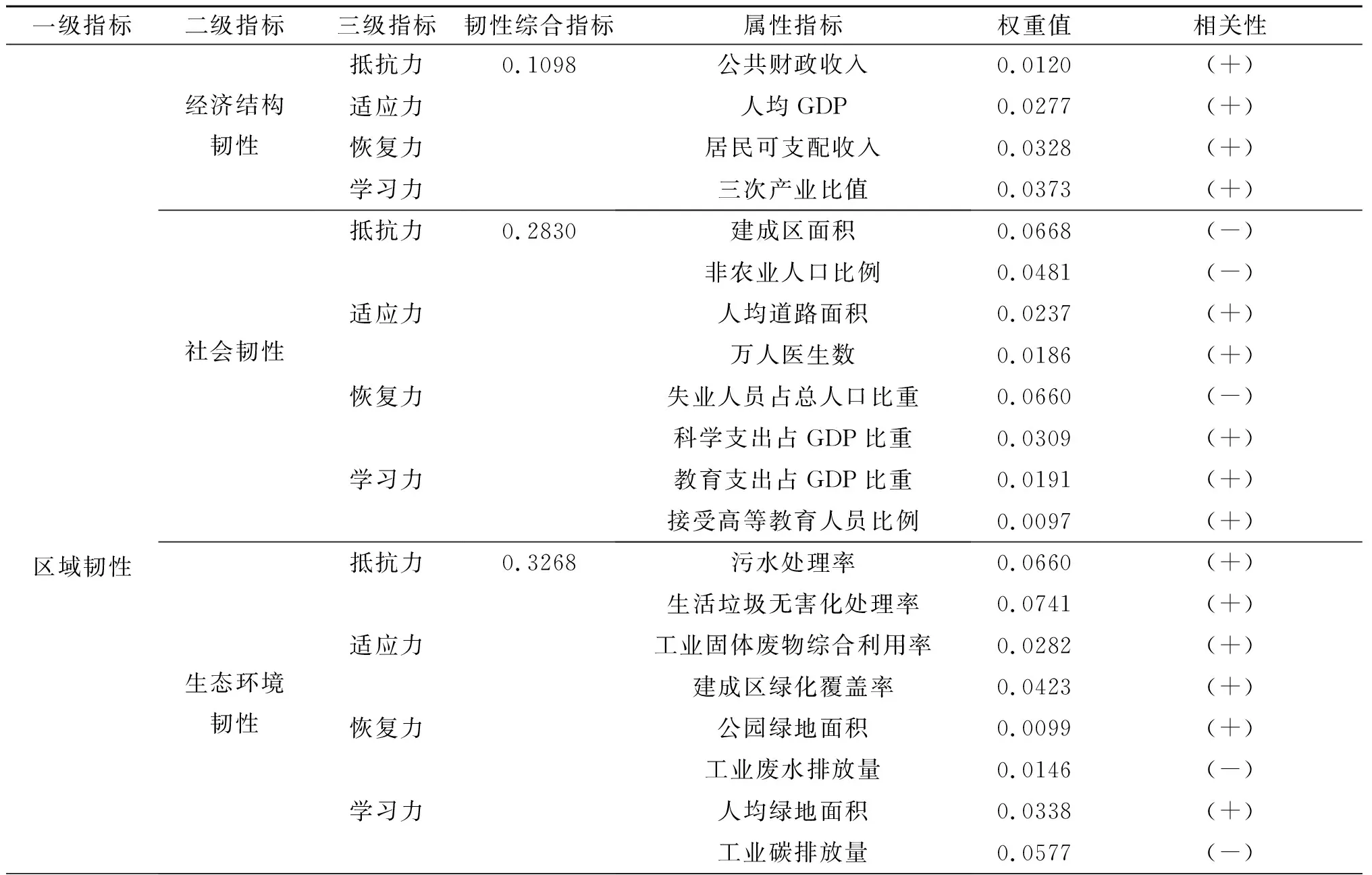
区域韧性作为系统受到灾害时的抵抗、适应、恢复和学习能力,也是灾前准备、灾时应对、灾后恢复及学习的过程[23]。传统韧性研究主要针对单一城市的单一要素,通常利用Bruneau等提出的典型灾害发生时系统反应过程曲线模型作为基础,建立韧性评价框架[24](如图3所示)。面对外来破坏,系统变化分为3个阶段,第一阶段( t 图3 单一城市单一要素韧性曲线 反应过程变化曲线计算韧性方法,分别用D1、D2、 ……、Dn表示不同要素的韧性,Ds表示各子系统韧性之间的相互关系[26],方程式为 DS=g(D1,…,Di,…,Dn) (1) DS=gD (2) 2.1.2 单一城市多要素韧性测算方法 上述方法仅能用于单一城市单一灾害时城市韧性研究,而各城市韧性由多个维度组成,每个维度都由不同要素构成,韧性要素由单一子系统变成多子系统,且存在较强联系,使整体特效呈现“1+1>2”效果,也使恢复时间缩短为t2,根据Haimes研究基础之上,用投入—产出模型表示各城市之间的相互联系。区域由不同城市组成,根据“1+1+1>3”的效果,各城市联系进一步提升,使韧性较快恢复,其结果如图4,以曲线S2表示。 图4 单一城市多要素韧性曲线 计算方法为 X=eD-E (3) (4) 其中:X为城市韧性值;e为单要素关系矩阵;ei表示单一系统内第i指标权重,Di表示第i要素值,E为要素耦合关系边际值。 2.1.3 “多维空间面板决策模型”区域韧性测算方法 由于区域是由多个城市构成,且内部包含多种要素,本研究对上述单一城市单一要素(公式2)和单一城市多个要素(公式4)的韧性研究进行改进,进行区域韧性研究。但区域内不同城市差别较大,受“短板效应”影响,无法准确表达区域韧性,在此基础上增加城市关系,使韧性水平最低值及整体恢复力极大提升。区域在受到干扰时,其最低值达到X3,较单一城市及单一要素韧性水平有所提升,恢复时间缩短为t3,恢复力、适应力及学习力整体提升。该公式是以哈利盖特的韧性研究为基础,由于现实情况中灾害冲击,使损耗大于理想模型预估值,“投入—产出”函数中通过1/μ来描述其递减情景,并借助相关系数v引入,修正了不同城市短板因素对韧性测度造成的影响[27]。由于不同城市各项建设差别较大,受“短板效应”影响,单纯内部要素关系无法准确表达区域韧性,在此基础上增加城市之间关系,使韧性水平最低值及整体恢复能力极大提升[28-29],因此得到△D,为曲线S3(见图5)。 图5 区域多要素韧性曲线 计算方法为 Y=eD+CZ+△D-E (5) (6) 其中:Y为区域韧性;eij表示i城市j要素指标权重;xiyj表示第i城市j要素值;D表示韧性要素向量;Pa表示区域不同城市之间关系矩阵;Qb表示城市内要素之间关系向量;△D表示各空间要素向量的变化量,也就是系统内部短板影响部分。v、u表示相关系数和常量,其中v值为0.15~0.3,u值为6;r和△k表示子系统与城市之间所产生的边际韧性值,r值为0.8~1.5,△k为3~5。 通过多维空间面板决策模型计算,将区域各城市韧性多维度要素联系起来,能够解决单一城市及单一要素韧性计算所存在的短板问题,通过计算方法的选择,使区域韧性计算更加方便且符合真实情况,能够应用于所有韧性测算中,具有较强普适性,不仅降低外部要素之间干扰对城市韧性造成影响,该模型和计算方法综合应用进一步提高计算准确性。但由于不同要素对总体韧性影响的差异性,为了明确总体韧性制约因素及决定性因素,仍需对各要素分异性进行测算。 在对区域韧性研究时,不仅要对总韧性分析,也要对各维度要素分解。由于各维度存在着复杂联系,根据其对区域及其他维度要素的影响,明确各维度空间要素变化对总体韧性关系。因此利用空间杜宾模型对各维度空间要素分析[30],其公式为 (7) 该公式中空间交互效应是区域内某一城市任意给定解释变量对其他地区被解释变量的影响,从而求出解释变量溢出效应,被埃尔霍斯特( Elhorst) 扩展至对空间面板数据模型分析,用于要素分异研究。由于区域韧性研究中,“抵抗力—适应力—恢复力—学习力”四个维度相互影响形成“S”曲线,因此可以利用空间杜宾模型对其构成要素分析。 2014年国家提出中原城市群建设,中原城市群包括30个城市,并分为核心发展区和辐射区。核心发展区以郑州为中心,包括河南省开封、洛阳、许昌、新乡、平顶山、焦作、漯河、济源、鹤壁、商丘、周口和山西省晋城市、安徽省亳州市等城市(如图6)。长期以来中原城市群核心区以农业为主,是我国人口较为密集区域,经济发展不平衡,各城市建设也存在较大差距,区域韧性存在较大问题[31]。核心发展区作为中原城市群重点发展区域,韧性水平直接关系到中原城市群走向。为明确中原城市群建设对区域影响及区域韧性变化,研究选取中原城市群核心发展区2011—2021年的多元数据统计分析,数据均采用年度数据。各指标数据均来自《中国城市统计年鉴》《河南省统计年鉴》及各市的《国民经济发展统计公报》。 图6 中原城市群核心发展区范围图 根据获取数据和1.2.2的权重计算方法,利用Matlab模型对所有指标权重值测算,各要素权重值如表1。 表1 区域韧性评估多元指标权重值 3.3.1 总体韧性水平测算 在对中原城市群核心发展区总体韧性测算时,利用公式6对区域韧性计算,中原城市群核心发展区总体韧性呈现“先增后减又逐渐上升”趋势(见图7)。2014年中原城市群建设提出,各城市迅速响应,各项建设速度加快,特别是郑汴洛一体化的提出,加快了区域设施一体化,经济及环境有了较大改善,总体韧性提高[32-33]。在2016年底,国务院正式批复中原城市群发展规划,区域建设稳步有序,定位及分工逐渐明确,城市稳步发展,中原城市群核心发展区总体韧性不断增强。 图7 2011—2021年中原城市群核心发展区韧性情况 3.3.2 区域韧性构成肌理的整体分异特征 根据表1评估指标体系及各要素权重,利用公式6对2011—2021年中原城市群核心发展区各城市韧性值计算。各城市韧性水平均呈现“先增后降再稳步增加”趋势,2014—2015年郑州市韧性水平大幅提升,2015—2016年呈下降趋势,而后大幅度降低,其他城市的韧性值在2013—2014年逐渐增加,2014—2016年有小幅度降低,2016年后平稳增长(见图8)。 图8 2011—2021年中原城市群核心发展区各城市韧性对比 郑州市韧性水平高于其他城市,洛阳居第2位,新乡、开封分别位居第3、4位。中原城市群提出时,城市框架拉大,生态环境得到改善,经济水平也有较大发展,都为中原城市群核心发展区韧性提升提供基础[34-35]。但由于中原城市群核心发展区多以农业地区为主,发展后劲不足,同时受世界整体经济形势影响,各产业雷同且相互联系格局未形成,出现短暂的良好发展势头。2016年后各城市发展回归正常,各城市根据在中原城市群核心区定位,合理化发展,各城市韧性水平稳步提升。 3.3.3 中原城市群核心发展区韧性空间分异特征 受“抵抗力、适应力、恢复力、学习力”等多维空间影响,不同年份各要素影响差异较大,使中原城市群核心发展区韧性也有较大差异,因此利用公式7对各要素影响差异性计算。为明确各要素对韧性影响,对不同城市不同年份各维度空间要素对比分析。 (1)多维空间总体韧性水平变化及影响因素 利用公式7计算,得出表2。通过对表2分析发现,中原城市群核心发展区抵抗力和恢复力2021年降低,适应力从2020年逐渐降低。学习力与总体韧性趋势保持一致,2015年达到最高,随后降低,出现较小波动。受新冠疫情影响,城市建设及经济发展缓慢,韧性水平受到较大影响,各要素在2020年和2021年均降低。学习力曲折变化的主要原因是由于城市内部管理重视程度不够,应急指挥建设受政策影响较大,城市财政收入占GDP的比重也受整体经济形势影响,具有一定差别。 表2 2011—2021中原城市群核心发展区多维空间要素情况 (2)抵抗力对区域韧性决定性影响 根据图9分析,抵抗力均呈增长趋势,各城市2021年均达到最高。由于郑州市人口数量较多,城镇化率较高,经济发展处于河南省首位,郑州市抵抗力一直处于前列,对区域韧性具有决定性影响。开封市抵抗力变化较大,2013年达到最低。洛阳、新乡、平顶山、漯河、许昌、焦作、济源在2016年前后变化较大,2016年后增长较为平稳,抵抗力变化不大,主要是由于城市规模变化不大,内部设施建设较为平稳,应急管理无较大变化导致,周口、商丘、晋城自2011年后变化不大,主要是由于城市发展速度相对较慢,城市规模变化不大造成的;鹤壁在2013年后增长较快,但2016年后变化较小,主要是由于在2013年之前城市规模扩大较快,经济增长较为迅速,2016年后城市发展放缓,应急设施建设无变化。 (3)恢复力对区域韧性引导性影响 根据图10分析,恢复力整体呈增长趋势,2020年达到最高。其中郑州、洛阳、新乡、平顶山恢复力较高。郑州市2016年达到最高,洛阳市2014年达到最高,新乡市和焦作市基本保持稳定,开封市、漯河市、许昌市逐渐增加,鹤壁、商丘、亳州变化较小。由于郑州市开发建设速度先快后慢,绿地、公园及基础设施建设提升速度较慢,失业人口数量增加,居民可支配收入水平未有大幅度提升,人口增加使人均公园绿地面积增幅变慢,但建筑平均层数较大幅度提升,使灾害恢复能力有所下降。洛阳、许昌规模不断增大,人均绿地面积不断增加,生态环境有较大改善,随着旧城改造进行,城市新区和老城区基础设施建设水平有很大提高,工业废水处理率及利用水平均有较大幅度提升,区域韧性水平也有大幅提升。 图10 中原城市群核心发展区各城市区域恢复力变化 (4)适应力对区域韧性关键性影响 根据图11分析,郑州市在区域韧性中起着关键作用,适应性远高于其他城市。14个城市中仅郑州、开封、洛阳、平顶山、周口、商丘呈直线上升,其他城市均相对稳定,济源、晋城变化较小,增长幅度较慢。主要是中原城市群建设,使各城市人均GDP、道路建设增加,不同城市联系增强,公共服务设施均等化建设,各城市医疗卫生水平有较大提高,但增加人口远高于医疗设施建设水平,使万人医生数仅有少量增加。工业固体废弃物利用率均保持较高水平且建成区绿化覆盖率也有较大增加,城市供气量和供气普及率增加、建成区密度降低,适应性不断提升。为提高灾害救援能力,特别是2015年以后,多数地区都发生严重洪涝,应急指挥系统提升,进一步提升了适应力。 图11 中原城市群核心发展区各城市区域适应力变化 (5)学习力对区域韧性根本性影响 通过图12发现,郑州市学习力仍排在首位,特别是2014年后快速提升。其他城市学习力在2014和2015年相对较高,随后逐渐降低,近年来又开始有所增加,同时增速较为均衡,但速度较慢,周口市近年来发展速度相对较慢,主要是由于城市绿地等空间不足,人均避难场所面积相对较小造成的,仅为0.05 m2/人。中原城市群建设开始前各城市发展相对较为缓慢,接受高等教育人数相对较少,工业碳排放量相对较高,但城市群建设开始后,综合防灾受到重视,城市环境得到极大提升,人均绿化面积有少量增加,工业碳排放量也随着经济发展增加,但近年来逐渐降低,人均避难场所面积虽有所增加但变化不大,人均面积仍保持在0.5以下,无法满足居民避难需求,各城市学习力缓慢发展使区域韧性水平无大幅度提升。 图12 中原城市群核心发展区各城市区域学习力变化 本研究结论有以下4个: (1)区域韧性作为城市群合理化发展及稳定建设基础,为确保区域受到干扰或保持灾害时的稳定性,从灾害全过程对区域韧性评价。在评价中根据系统特性及韧性建设要求,建立基于“抵抗力、适应力、恢复力、学习力”的多维度空间面板模型,并构建区域韧性评估指标体系,同时根据“投入—产出”模型提出区域韧性测算方法,并以中原城市群核心发展区为例,进行差异化分析,明确韧性变化。 (2)中原城市群核心发展区各城市韧性水平均呈现先增后降再稳步增加趋势,2014—2015年郑州市韧性水平大幅提升,2015—2016年呈下降趋势,而后大幅度降低,其他城市在2013—2014年逐渐增加,2014—2016年有小幅度降低,2016年后平稳增长。 (3)2011—2021年总体韧性水平先增后降,2015年后稳步增长。各构成要素中,区域抵抗力直线上升,适应力变化不大,郑州市占主导地位。 (4)中原城市群核心发展区韧性仍存在较大问题,其抵抗力、适应力、恢复力及学习力方面仍存在一定问题,主要是中原城市群核心发展区多数地区经济发展不平衡,产业结构不合理,第一产业占据较大比例,同时由于城市内部管理重视程度不够,应急指挥建设受政策影响较大,城市财政收入占GDP的比重也受整体经济形势影响,具有一定差别。且近年来受新冠疫情影响,城市建设及经济发展缓慢,韧性水平受到较大影响,各要素在2020年和2021年均降低。 多元统计数据为多维度空间面板决策模型的建立提供了基础,不仅为中原城市群核心发展区韧性评估提供了保证,也为其他城市群韧性研究提供了支撑,为区域各层面韧性研究提供了新的方法和技术手段,确保了韧性评估的科学合理。

2.2 韧性构成各维度要素分异计算方法
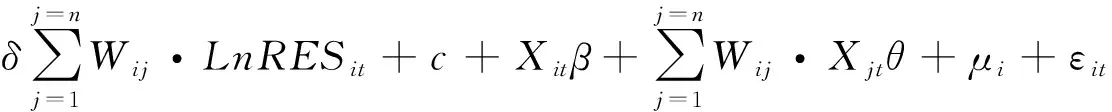

3 多维空间面板决策模型”中原城市群发展核心区韧性评估应用
3.1 研究范围及多元数据来源
3.2 各要素权重值计算
3.3 基于决策模型的中原城市群核心发展区韧性测算






4 结论
