基于综合主成分分析和正交试验设计的指标灵敏度分析<br/>——以南水北调中线工程为例

基于综合主成分分析和正交试验设计的指标灵敏度分析
——以南水北调中线工程为例

2024-01-30聂相田何流郭莹范天雨华北水利水电大学水利学院河南郑州450045

项目管理技术 2024年1期

聂相田何流郭莹范天雨(华北水利水电大学水利学院，河南郑州 450045)

0 引言

综合评价是指综合多个指标信息对研究对象进行定量评价，目前已在各领域得到广泛应用。评价对象不同，所建立的评价指标体系也不一样，且每个指标都是总体状况在某一方面的反映[1]。在大量指标中选取少部分对评价影响大且能够合理、准确反映评价对象实际状态的指标，能够大大减小计算量，提升评价工作效率。

局部灵敏度分析和全局灵敏度分析是常见的灵敏度分析法。局部灵敏度分析是指在其他参数固定下，分析单指标因素对模型结果的影响；全局灵敏度分析是研究多指标因素变化对总体结果的影响，并分析参数之间的相互作用对模型结果的影响[2]。

指标灵敏度分析是指定量化研究评价指标的变化对评价结果的敏感程度，属于局部灵敏度分析范畴。进行指标灵敏度分析可以确定指标变化对评价结果的影响，通过指标优选精简指标体系[3]。目前，针对灵敏度分析方法的研究成果较为丰富。孙捷先[4]进行了高精度同步相敏检波系统灵敏度分析；Sobieski等[5]将几何规化的灵敏度分析方法用于结构优化设计；吴祈宗等[6]提出了基于GRG法灵敏度分析法。上述方法要求目标函数连续可倒且对寻优算法依赖较大。为了解决这一问题，邱清盈等[7]提出了一种利用正交试验分析的灵敏度分析方法。

对于评价指标而言，指标数据一般都是通过连续或间断性检测获取的，指标值大多数是离散的点，这与正交试验设计确定灵敏度的思路一致。因此，本文利用正交试验设计[7]建立指标灵敏度分析模型，以期为指标优选提供数据支撑。

1 指标灵敏度分析

灵敏度分析是指判断指标变化对综合评价结果的影响程度，因此，首先要建立综合评价函数。主成分分析法能够在指标权重未知的情况下对评价对象进行综合评价。基于此，本文采用主成分分析法对综合评价结果进行预评估，进而结合正交试验设计对指标灵敏度进行分析。

1.1 基于主成分分析法确定预评估值

主成分分析法通过正交变换将一组可能相关的高维数据转换成不相关的变量，从而实现数据降维，避免信息重叠，能较好地保留原始数据信息。主成分分析更容易捕捉到事物的主要矛盾，并揭示原始变量之间的内在关系。这些特点和优势使主成分分析在综合评价研究领域得到广泛应用。

丛明珠等[8]将主成分分析法用于土地利用程度评价，对江苏省各县市土地利用程度进行综合评价；宫凤强等[9]结合主成分分析法和距离判别法对采矿突水水源进行识别研究；赵京等[10]利用主成分分析法对机械臂运动的灵活性进行综合评价；黄安等[11]基于主成分分析法对陕西省蓝田县部分乡镇的土壤养分进行综合评价；商立群等[12]将改进的主成分分析法用于火电机组综合评价；沈江等[13]利用主成分分析和集对分析对生态工业园区进行评价；王颖颖等[14]利用主成分分析法对市场芝麻酱品质进行综合评价；赵自阳等[15]结合主成分分析和因子分析法对宁夏水资源承载力进行研究；朱南军等[16]将主成分分析用于国内保险机构的综合评估。

通过梳理上述文献，本文利用主成分分析法进行指标预评估，步骤如下：

(1)设评价指标个数为n，评价对象指标值的采样次数为m，得到评价指标原始数据矩阵A=(aij)m×n。即

(1)

(2)对原始数据矩阵进行标准正态化处理。公式如下

(2)

式中，E(ai)表示矩阵A中第i列元素的平均值；D(ai)表示矩阵A中第i列数据的方差。由式(2)求出原始数据标准正态化处理矩阵B=(bij)m×n。

(3)计算相关性系数，公式如下

(3)

式中，rij表示矩阵B中第i列元素与第j列元素之间的相关性系数；cov(bi，bj)表示协方差。由式(3)求得矩阵B中各列元素间的相关性系数矩阵R=(rij)n×n。

(4)由相关性系数矩阵计算主成分方差贡献率ω和累计贡献率ρ。设λ1≥λ2≥…≥λn分别是矩阵R的n个从大到小排列的特征根，其对应的特征向量为β1，β2，…，βn。通过式(4)求得第i个主成分的方差贡献率，通过式(5)计算各主成分累计贡献率。公式如下

(4)

(5)

(5)对评估对象进行预评估。当ρs>85%时，保留前s个主成分。计算公式如下

zi=ω1a′iβ1+ω2a′iβ2+…+ωsa′iβs

(6)

式中，zi表示评价对象第i次采样的评估值；a′i=(ai1，ai2，…，ain)表示矩阵A中第i个行向量。

1.2 正交试验设计

正交试验设计是一种用正交表安排实验的方法。根据多指标、多水平安排实验，分析指标多水平变化对实验结果的影响。正交试验能够减少试验次数，并获得最优的实验方案。

正交表是用于正交实验的一种特殊表格，通过设计指标组合保证实验指标的正交性[7]。正交表一般用La(bc)表示，其中，L代表正交表；a代表实验次数，通常情况下，每个实验都需要进行多次操作才能收集足够的数据，以精确地分析结果；b代表水平数，即每个实验参数所包含的可选项数量；c代表指标数量，即需要评估的输出或响应变量数量。常用的正交表有L4(23)、L9(34)、L2(211)等，其中，L4(23)正交表见表1。

表1 L4(23)正交表

正交试验设计分析法分为极差分析法和方差分析法。为了确定指标的影响程度，本文使用极差分析法进行分析。通过计算指标j的极差Rj，评估指标对试验结果的水平和重要贡献程度。指标的极差Rj计算公式如下

(7)

1.3 指标类型、极差与综合评价的关系

设Qi(X)为综合评价函数，xj为指标变量，在指标xj=k时，Qi(X)对指标j的灵敏度Sij为

(8)

式中，Sij表示单调性。若Sij>0，则Qi(X)对xj单调递增，即随着xj增大，Qi(X)不断增大；若Sij<0，则Qi(X)对xj单调递减。Sij越大，说明指标j对Qi(X)的灵敏度越大。

指标类型反映了Qi(X)对xj的增减性。具体而言，当指标为效益型时，随着指标值的增大，函数值Qi(X)表现出更好的性能。如果函数Qi(X)追求最小值，指标值的增大会导致函数值Qi(X)变小；相反，如果函数Qi(X)追求最大值，则指标值的增大会导致函数值Qi(X)变大。

极差Rj反映了xj对综合评价结果的影响程度，即指标的灵敏度|Sij|。当用二水平正交表实验时，若指标值xj1和xj2差距微小，则

(9)

得到

(10)

1.4 指标灵敏度分析过程

基于主成分分析法和正交试验设计的指标灵敏度动态分析过程如下：

(1)确定评价指标体系。

(2)利用主成分分析法对评价结果进行初步估计。

(3)选择适合指标个数的正交表。正交表La(bc)的选择需满足条件a=c×(b-1)+1。以二水平正交表为例，b=2，c=a+1且a为4的正整数倍，c不小于指标个数。

(4)确定指标水平，按正交表安排试验方案。

(5)分别计算出不同方案对应的综合评价值。

(7)通过极差公式计算极差Rj。

(8)根据极差Rj，计算各指标变量对综合评价结果的灵敏度|Sij|。

2 案例分析

南水北调中线工程途经河南、河北两省及天津、北京两个直辖市，穿越长江、淮河流域，沿京广线北上，为沿线十几座大中型城市提供生活和工农业用水。

渠道工程是南水北调工程的主要部分，其安全性影响着整个调水系统的安全运行。下面对渠道工程相关风险指标进行灵敏度分析，以便进行指标优选，使渠道工程风险评价结果更加准确。

2.1 渠道工程风险评价指标体系

南水北调中线工程调水距离长、跨越地域广，且气候差异较大；渠道沿线地质条件复杂，涉及膨胀土段、煤矿采空区段、高填方段、湿陷性黄土段等不良地质条件；渠道高填方段约100km，最大填方高度达25m。因此，渠道工程风险事件包括地基沉降、滑坡、渠堤失稳、漫顶、渗漏等。经过文献分析和实地调研得到渠道工程风险指标，包括挖方渠段地下水位上涨p1、挖方渠段坡面坡顶加载超负荷p2、挖方渠段坡面保护措施被破坏p3、超标洪水损毁坡顶防洪堤p4、防洪堤外排洪通道淤堵p5、填方渠段渠堤内坡失稳p6、填方渠段渠堤外坡渗漏破坏p7、填方渠段渠堤外坡坡脚泡水软化p8、填方渠段地基沉降p9、填方渠段坡面水流冲刷p10、渠水漫顶p11。渠道工程风险评价指标体系如图1所示。

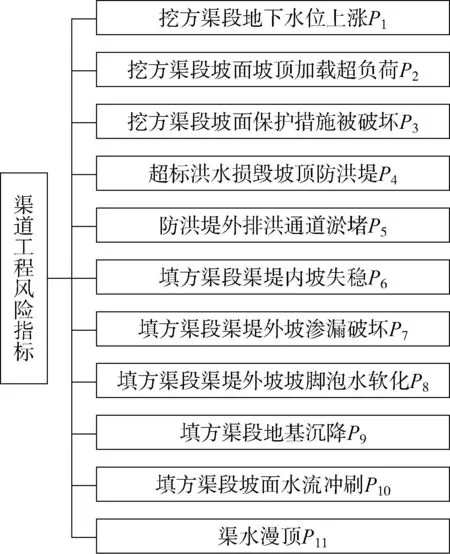
图1 渠道工程风险评价指标体系

2.2 渠道工程风险预评估

模拟5名检查员对渠道工程进行检查打分，分值范围为0～1。分值越大，说明风险越大。构建打分结果原始数据矩阵A，即

根据式(2)对矩阵A进行标准正态化处理，得到矩阵B，再根据式(3)得到系数矩阵R。

通过式(4)～式(6)计算得到综合评价结果Z=0.115 07。

2.3 评价指标灵敏度分析

(1)选取正交表。由评价指标体系可知，该模型包含11个指标变量。根据二水平正交表的构造规则选取L12(211)正交表，表中的行表示试验方案，列表示指标。

(2)确定11个指标变量的水平。各指标均取变化量5%，确定各指标的2个水平。其中，水平1为各指标值增大5%后的平均值，水平2为各指标值减小5%后的平均值。

(3)根据主成分分析法对12个实验方案进行评价，经过计算得到评价结果。

(4)计算基本指标处于不同水平时的综合评

(5)通过式(7)求出各指标不同水平下的极差Rj。

(6)计算各指标变量对综合评价结果的灵敏度|Sij|。

综上所述，正交试验结果分析表见表2，指标灵敏度见表3。

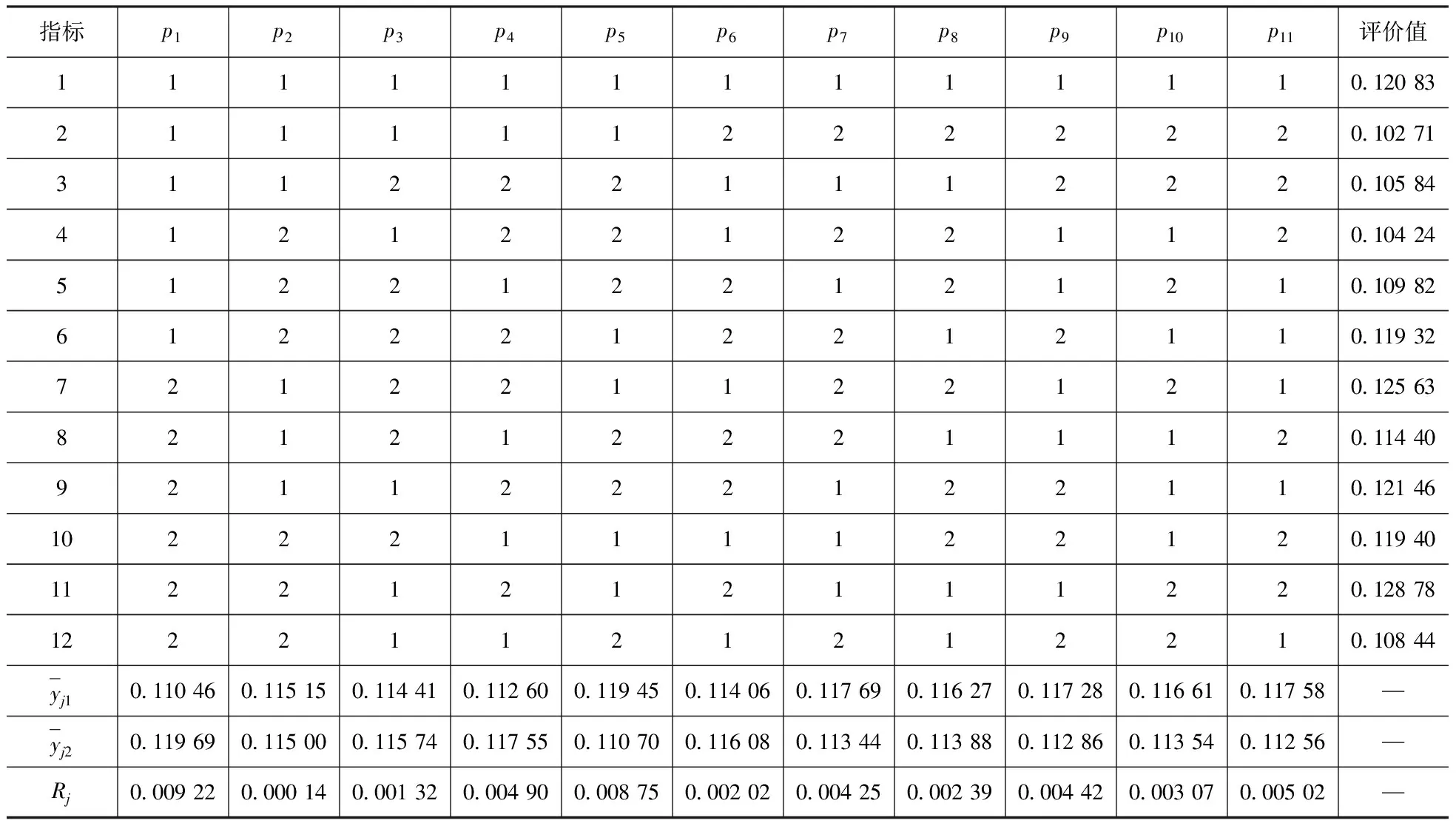
表2 正交试验结果分析表

表3 指标灵敏度

2.4 结果分析

由表3可知，挖方渠段地下水位上涨、超标洪水损毁坡顶防洪堤、填方渠段渠堤外坡渗漏破坏和渠水漫顶4个指标灵敏度较大，即指标值的变化对综合评价结果的影响较大；挖方渠段坡面坡顶加载超负荷、挖方渠段坡面保护措施被破坏和填方渠段坡面水流冲刷3个指标灵敏度较小，即指标值的变化对综合评价结果的影响较小。各指标灵敏度从大到小分别为渠水漫顶、超标洪水损毁坡顶防洪堤、填方渠段渠堤外坡渗漏破坏、挖方渠段地下水位上涨、防洪堤外排洪通道淤堵、填方渠段渠堤外坡坡脚泡水软化、填方渠段渠堤内坡失稳、填方渠段地基沉降、填方渠段坡面水流冲刷、挖方渠段坡面保护措施被破坏、挖方渠段坡面坡顶加载超负荷。