应用差分进化-神经网络模型的杀爆弹瞄准点分配方法

徐豫新，贾志远，杨晓红，索非，张益荣

（1.北京理工大学 爆炸科学与技术国家重点实验室，北京 100081；2.北京理工大学 重庆创新中心，重庆 401120；3.中国人民解放军63961 部队，北京 100012）

精确制导杀爆弹作为各军种打击目标的主要手段，已经实现了上百公里外仍具有几米制导精度（circular error probable，CEP）、可对战役纵深目标（面目标）实施精确压制，并具备“一次齐射、多点攻击”的能力.随着精确制导弹药作战效能的提高和目标打击范围的拓展，停机坪飞机群、防空反导阵地和有生力量集团等典型面目标作为现代作战体系中的核心力量已成为战场上主要的打击目标类型，因此通过对精确制导杀爆弹打击面目标瞄准点进行优化选择，为作战指挥决策层提供具有最佳效费比的打击方案具有重要军事应用价值.

长期以来，国内外就多弹协调打击目标瞄准点规划方法进行了大量研究.对目标进行射击时，均匀分布瞄准点方案是一种较为简单的火力分配方案，其核心思想是使瞄准点均匀分布，给各个瞄准点分配等量的弹药[1]；KLINE 等[2]开发了一种基于测验问题解决方案的启发式算法解决防空作战中为来袭弹药分配拦截导弹，以最大化摧毁导弹的概率.SUMMERS 等[3]将在防空作战中确定拦截弹分配给来袭导弹的射击策略规划问题表述为马尔可夫决策过程，并使用基于仿真的近似动态规划（approximate dynamic programming，ADP）方法来解决基于代表性场景的问题实例.SU 等[4]针对多导弹协同拦截高机动目标的问题，为实现对目标规避区域的协调覆盖，引入虚拟瞄准点概念，将协同问题转化为优化问题，为不同导弹寻找一组合适的虚拟瞄准点.ZHAI 等[5]以毁伤面积百分比作为衡量导弹打击建筑目标毁伤程度的标准，利用蒙特卡罗方法对导弹着陆点进行模拟并建立建筑目标毁伤概率等高线，将毁伤概率等高线作为导弹攻击策略评估的重要依据.李彩峰等[6]基于火箭弹射击误差与毁伤半径建立火箭弹对目标毁伤程度和火箭弹弹着点之间的函数关系，通过遗传算法对该函数进行最优化求解，实现了在有效毁伤面积最大化条件下对面目标的分火点计算；李臣明等[7]以平均相对毁伤面积为射击效率指标，通过对面积目标网格微元积分，以最大射击效率为目标函数进行优化搜索，在求取射击效率的基础上确定出射击点的数量和坐标.

除上述外还有许多围绕射击效能评价指标的建立与补充[8-12]，以及优化算法的应用与改进[13-17]两方面进行精确制导弹药瞄准点规划方法的研究 ，其中射击效能评价指标的复杂度与合理性影响瞄准点分配模型解算速度与分配结果可靠性，优化算法的求解效率影响瞄准点规划模型求解的速度与精度.为追求实时决策实时打击的现代作战指挥需求，现有射击效能指标制定与求解通常根据弹药毁伤半径、命中概率等弹药性能参数，模型计算时耗小但忽略了弹药在对目标实际打击过程中动爆威力场与目标耦合毁伤效果，特别是装配杀爆战斗部的弹药动爆毁伤区域通常为月牙形、元宝形等[18]，与圆形区域偏差较大，若使用毁伤半径进行弹药威力表征与射击效能计算，规划结果合理性与打击效能无法满足现代作战精确压制要求.故提出一种融入动爆威力计算的多瞄准点分配方法，在大幅提高多枚杀爆弹打击面目标瞄准点分配精确性的同时，模型求解速度也满足作战指挥对打击方案制定时耗要求.此外所建立的模型和算法可为精确制导杀爆弹武器系统设计提供参考.

1 融入动爆威力的瞄准点分配

精确制导杀爆弹药可实现对面目标分布式精确打击，其瞄准点规划是指对目标打击时满足作战任务要求的每枚杀爆弹的瞄准点、落速、落角和炸高等参量求解，实质是对弹药毁伤模式、末端弹道以及炸点坐标进行规划.本文中综合考虑了杀爆战斗部动爆威力场与打击目标易损特性，通过引入神经网络模型实现了多杀爆弹联合打击下面目标毁伤效果快速预测与瞄准点分配方案的制定.具体实现流程如图1 所示.

图1 瞄准点规划模型建立流程Fig.1 Establishment process of aiming point planning model

首先建立以毁伤幅员为表征量的多杀爆弹对面目标联合打击毁伤效能评估模型；其次通过毁伤效能评估模型生成大量计算数据对神经网络模型进行训练并生成代理模型，实现对多枚杀爆弹联合打击下（确定打击瞄准点及弹药末端弹道参数）面目标毁伤效能快速计算；最后通过差分进化算法对多杀爆弹打击面目标毁伤效能表征量极值进行优化求解，在满足作战指挥决策时耗要求下给出一个最优的打击方案.

2 对面目标毁伤效能分析模型

瞄准点分配结果的优劣，主要取决于弹药消耗量和射击条件确定情况下弹药对目标毁伤效能评估结果的高低.因此，多杀爆弹联合打击面目标毁伤效能分析模型是制导杀爆弹药对面目标打击方案制定的基础.

2.1 毁伤效能表征

依据面目标特性选取毁伤幅员作为多杀爆弹联合打击毁伤效能表征量，毁伤幅员定义为破片/杀伤战斗部威力场通过概率加权得到的毁伤概率为1 的等效空域[19].对于面目标，预期杀伤目标数量为：

式中：φ(x,y,z)为弹药炸点的三维坐标概率密度分布函数；δ(x,y)为微元面积内的目标密度，通常设定微元面积内目标为1，即对于1 个目标所占用的微元大小（如一个立姿人员所占的大小通常为：0.5 m×0.25 m=0.125 m2）；P(x,y)为弹药作用在微元面积上的毁伤概率.

就均匀分布目标而言，δ(x,y)为常数，因而有：

式中：Et/δ具有面积的量纲，为毁伤幅员，记作AL.杀爆弹不需要直接命中即可对目标进行毁伤，毁伤幅员体现在毁伤元（破片和冲击波）对目标毁伤能力.毁伤幅员AL综合考虑了杀爆弹动爆威力场以及处于威力场中的目标易损性，而且可根据AL值定量描述杀爆弹对面目标毁伤效能的高低，因此可用于杀爆弹对面目标毁伤效能的表征与评估.

2.2 毁伤效能分析模型

2.2.1 目标模型

假定面目标为矩形区域且均匀分布，定义目标区域坐标系，坐标系原点为目标区域几何中心，X轴指向矩形长边方向，Y轴垂直于平面向上，Z轴方向由右手定则确定.为求解弹药毁伤幅员，分析战斗部毁伤元与目标区域耦合交会情况，对长和宽为La和Wa的矩形面目标进行微元化划分，即划分网格.设定长度方向划分间距为NL，宽度方向划分间距为NW，如图2 所示.

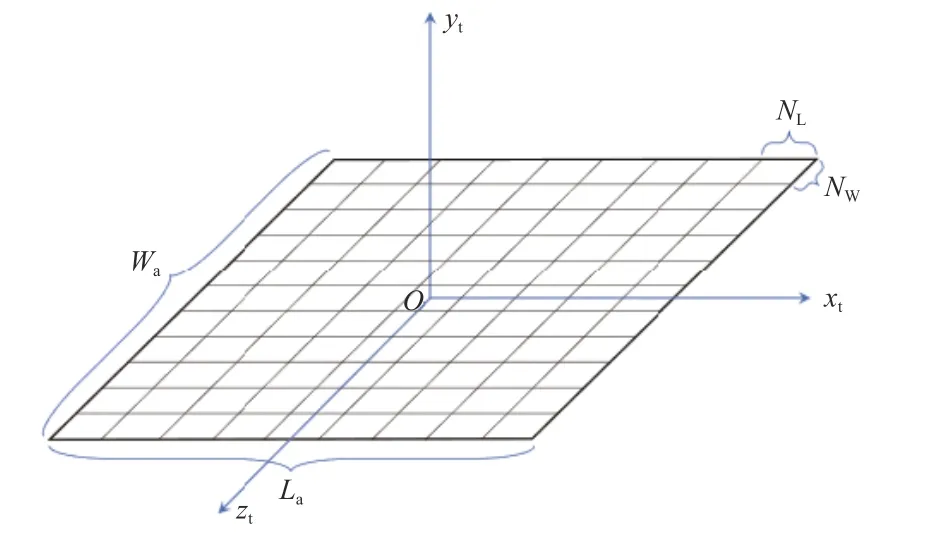
图2 面目标坐标系与微元化示意图Fig.2 Area target coordinate system and microelement

为考虑典型精确制导杀爆弹冲击波与破片对面目标毁伤效果，赋予面目标网格易损特性参数即毁伤准则与毁伤律.

爆炸冲击波毁伤通常采用超压准则、比冲量准则和超压-冲量准则，具体选用标准可根据目标结构自身振动周期T和冲击波正压作用时间t+决定[20].冲击波的作用按比冲量计算时，须满足t+/T≤0.25；而按峰值超压计算时，须满足t+/T≥10.毁伤律模型一般采用0～1 分布，即

式中：r为到炸点距离；Δpm(r)为冲击波峰值超压；pth为超压毁伤判据.比冲量准则或超压比冲量联合准则形式不变.

破片毁伤律模型通常采用有效破片命中数量的泊松分布概率函数或穿透破片密度的线性分布概率函数[21-22]，前者常用于人员目标，具体形式为

式中：S为目标易损面积，对于人员立姿取0.75 m2；k为对人员目标有效破片分布密度.有效破片指能够达到杀伤能量标准的破片，人体杀伤能量标准一般取78～98 J，或以是否穿透标准25 mm 松木板为标准进行核定.后者常用于车辆、飞机等目标，具体形式为

式中： ε为穿透目标等效靶的破片密度； εth为毁伤判据，一般取值3～5 枚/m2.

2.2.2 战斗部动爆威力计算

根据毁伤幅员定义，为考虑战斗部动爆情况下毁伤元真实空间分布情况，通过定义弹体坐标系下各典型毁伤元静爆威力场参量，再结合弹药末端弹道参数对战斗部毁伤元空间分布进行解析计算.

弹体坐标系原点O一般设在弹药战斗部的几何中心，Oxp轴沿弹体纵轴向前指向弹体头部，Oyp轴取在对称平面内向上（与面目标区域坐标系对应，便于弹目交会中求解），Ozp轴构成右手坐标系，如图3 所示.

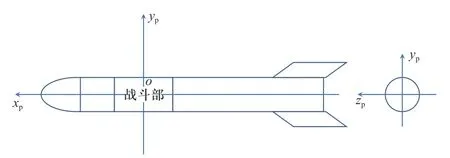
图3 弹体坐标系示意图Fig.3 Missile body coordinate system

杀爆战斗部静爆时，破片威力场参量包含每枚破片在弹体坐标系下的初始位置、初始速度、质量和速度衰减系数.冲击波威力场参量包含到炸点不同距离处的峰值超压、正压作用时间和比冲量.以上杀爆战斗部静爆威力参数均可通过理论公式、数值仿真以及试验研究等方式获取，这里不再详述.

杀爆战斗部动爆威力计算中，本文暂不考虑落速落角对冲击波场的影响.弹体坐标系下，弹药落角对破片的速度不会产生影响，弹药落速会改变单枚破片的速度大小以及方向.根据破片的静态飞散速度vps和弹体速度vm合成计算破片的动态飞散速度vpd，如图4 所示.

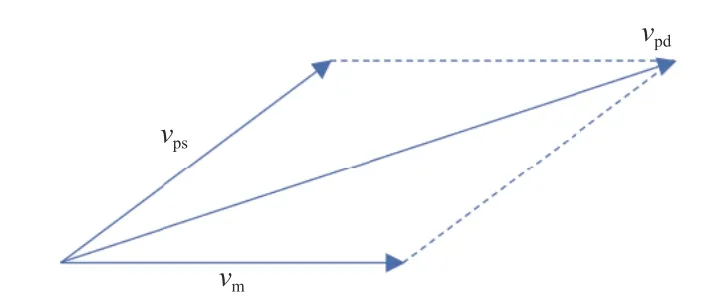
图4 破片动态飞散速度示意图Fig.4 Fragment dynamic dispersion velocity

2.2.3 弹目交会计算

通常认为，末端弹道直线即为导弹飞行轨迹曲线在末端处的切线.

制导弹药采用CEP 作为命中精度的描述参数.二维正态分布参数 σ的取值可由CEP 得到：

制导杀爆弹实际落点为瞄准点(aim)、系统误差(SE)和随机误差(RE)的耦合.在目标坐标系中进行计算，具体计算方法如下：

制导杀爆弹打击面目标时引信类型通常为定高引信，对于单路向下探测引信（某些弹药有左、中、右3 路探测，其原理相同），其具体作用模式如图5所示.

图5 杀爆弹定高引信作用模式示意图Fig.5 Operation mode of blast-fragmentation warhead set altimeter fuze

末端弹道线方程为：

式中：(xeb,yeb,zeb)为末端弹道线上的一点；(Xfallp,Zfallp)为落点坐标（在目标坐标系中）； ωb为落角； λb为方位角.

考虑装配引信参数的炸点坐标为：

2.2.4 毁伤幅员计算

采用迹线法计算杀爆战斗部对面目标毁伤效果，将破片动爆威力场参量（每枚破片的初始位置和初始速度）由弹体坐标系转换到目标坐标系下，对于破片的运动轨迹能够近似为一射线，即已知初始位置与速度矢量能够构造射线方程，计算该射线与面目标的交会点（射线与四边形求交）.为缩短计算时耗，快速得到破片命中面目标上的微元位置，对目标微元进行结构化处理，即对网格按照XZ平面位置顺序进行编号，便可通过交会点求得破片命中微元编号为:

式中：iE为网格长方向上编号；jE为网格宽方向上编号；L为面目标区域长；W为面目标区域宽；DL为长方向上网格划分数量；DW为宽方向上网格划分数量.

统计单次多杀爆弹联合打击下所有微元命中的破片数量与各破片速度、质量，即可根据微元上的目标易损特性参数（毁伤准则与判据）得到各微元毁伤概率P(iE,jE).

则本次打击方案下毁伤幅员AL为：

3 最优瞄准点分配模型

3.1 分配模型

本文采用结构简明、并行高效、收敛快速以及可靠稳定的差分进化算法[23]对瞄准点分配方案进行优化求解，该算法属于群体智能启发式进化算法，能够较好解决面目标瞄准点寻优问题.以毁伤幅员作为评价函数，通过差分进化算法进化迭代到预设的遗传代数，得到给定数量杀爆弹药联合打击下对面目标造成最大毁伤幅员的瞄准点位置与末端弹道参数，即为最优火力打击方案.

3.1.1 模型编码

该算法无法直接处理弹药瞄准点位置参数，因此，在求解过程中需要先将最优瞄准点的坐标进行编码.对于计划使用K枚制导杀爆弹来对面目标进行打击的情况而言，其对应的最优瞄准点坐标分别为(X1,Z1),(X2,Z2),···,(Xi,Zi),···,(XK,ZK)，对最优瞄准点坐标进行编码，得到长度为 2K的个体编码为：

式中：Xi为第i个最优瞄准点的横坐标值；Zi为第i个最优瞄准点的纵坐标值；K为弹药的数量.

3.1.2 种群模型

预设种群规模，并建立种群模型为：

式中：NP为种群规模；A(g)为第g代种群；An(g)为第g代种群中的第n个个体；an,m(g)为第g代种群中第n个个体中的第m个分量.

优化的参量包括瞄准点坐标、末端弹道参量（落角、落速、炸高），即在瞄准点坐标与末端弹道参量中选取需要优化的参量，对优化的参量进行个体编码；所述单个个体对应一组瞄准点坐标、末端弹道参量中需要进行优化的参量，与未进行编码即无需优化参量组合构成一次打击方案.

在个体编码后，通过给定的待优化参量的取值范围，随机产生种群中的所有个体，即得到最优瞄准点分配方案的初始种群.通过随机产生种群中的个体容易遍历所有的状态，进而求解得到全局最优解.

3.1.3 评价函数

评价函数是判断种群中个体优劣程度的标准，对种群的进化有着重要作用.除此之外，评价函数的复杂度是算法复杂度的主要组成部分，所以评价函数计算时耗的缩短会很大程度上缩短算法整体优化时间.

基于规划理想瞄准点问题的特征，选定多枚制导杀爆弹对面目标的毁伤幅员作为毁伤指标，并以第2 节中毁伤效能评估模型作为评价函数：

式中：Δwar为战斗部威力场；Δaim为目标易损性模型；ΔEb为弹药末端弹道； ΔF为炸高.

3.1.4 进化算子

进化算子是模拟种群中个体进化的过程.在种群进化过程中，包含3 种算子：变异算子、交叉算子和选择算子.

①变异算子.

通过差分的方式实现个体变异，这是差分进化算法重要的标志；本文采用常见的DE/rand/1[24-25]作为差分策略；在第g次迭代中，从种群中随机选取3个个体Ar1(g)、Ar2(g)和Ar3(g)，并且所选择的个体不一样；这3 个个体生成的变异向量为：

式中：Vn(g+1)为第g+1代种群中的第n个变异个体；Ar1(g)、Ar2(g)和Ar3(g)分别为第g代种群中第r1、r2和r3个个体；F为缩放因子，它决定偏差向量的放大比例，从而控制步长；F越大，扰动越大，其取值范围为[0,2].

②交叉算子.

采用二项式交叉[26]，对第g代种群中第n个个体An(g)及其变异个体Vn(g+1)进行个体间的交叉操作，产生对应交叉个体Hn(g+1).

式中：hn,m(g+1)为第g+1代种群中第n个交叉个体的第m个分量；vn,m(g+1)为第g+1代种群中第n个变异个体的第m个分量；mrand为[1,2,···,2N]之间的随机整数；CR为交叉概率，是控制交叉个体中的分量来自变异个体而非原个体的参数；CR越大则会造成个体更多的改变，其取值范围为[0,1].

③选择算子.

采用如下贪婪算法将子个体与父个体进行比较，将较优秀的个体保存到下一代中，作为优选，为了提高优选效率，直接选定毁伤幅员作为个体评价指标，即将单个个体对应单次毁伤幅员预测结果作为该个体的评价数值：

式中：f(Hn(g+1))为个体Hn(g+1)对应火力打击方案下的毁伤幅员值；f(An(g))为个体An(g)对应火力打击方案下的毁伤幅员值.

对于种群中每一个个体而言，通过变异、交叉和选择操作后所得到的子个体要好于或持平于父个体；然后经过足够的遗传代数能够得到给定数量杀爆弹对面目标造成最大毁伤幅员的最优瞄准点分配方案.其中，最大遗传代数要依据收敛情况进行确定.

3.2 基于神经网络的毁伤幅员快速预测

3.1 节中提到减小评价函数计算时耗是缩短优化算法整体求解时间的有效手段.为满足作战指挥快速决策的需求，将瞄准点规划时长控制在秒级以内，基于第2 节中动爆毁伤效果仿真计算数据，采用神经网络方法建立单枚弹药对面目标毁伤幅员计算代理模型，使用代理模型作为评价函数进行瞄准点分配优化求解.

3.2.1 毁伤效果等效方法

神经网络是对生物神经元的模拟和简化，包括多层感知机模型、卷积神经网络模型等等，理论上可以逼近任何函数.利用神经网络训练出的代理模型，可以快速进行多元向量之间的映射.

多弹毁伤幅员计算可以等效为一种从向量（包括目标易损性参数、战斗部威力场参数、弹目交会条件、引信参数等）到毁伤效果图像的映射.而矩形的目标区域图像分割成像素又很容易由矩阵来表示，定义输出矩阵为：

矩阵的每一个元素等价于目标划分出的一个网格微元，元素的值记录网格是否毁伤，“0”代表未毁伤，“1”代表毁伤（此处为简化神经网络训练，微元毁伤概率大于0 都标记为毁伤）.

毁伤矩阵作为神经网络的输出层，最好保证所有矩阵大小一致，也即a和b的大小固定，否则需要使用更为复杂的神经网络架构.考虑典型杀爆弹药毁伤范围，本文中选用200 m×200 m 的区域作为输出矩阵，固定了输出矩阵的大小，相对简化了神经网络模型的架构.利用200×200 像素训练集得到生成器的生成图像也为200×200 像素，但是弹药需要打在不同大小的面目标上，对这些不同形状的图像进行如下处理：

①小于200 m×200 m 的均匀分布面目标.

第一步：获取弹药在目标坐标系下的落点坐标及方位角，对毁伤效果图像的形状进行平移与旋转，超出边界的像素点舍弃；

第二步：固定目标坐标系，切除超出目标范围的像素点，剩余部分大小与目标大小一致，处理完成.

②大于200 m×200 m 的均匀分布面目标.

第一步：固定目标坐标系，对目标区域遗漏的部分补0，图像大小与目标大小一致；

第二步：获取弹药在目标坐标系下的落点坐标及方位角，对毁伤幅员图像的形状进行平移与旋转，超出边界的像素点舍弃，处理完成.

3.2.2 神经网络模型建立

神经网络的输入为杀爆弹打击目标的弹目交会条件（弹药姿态、落角以及落速）与引信参数（炸高）中任意需要规划参量，输出为一个200×200的毁伤矩阵，记录杀爆弹的毁伤效果图形.考虑到第2 节中建立的毁伤效能评估模型可以求出任意合理工况下的毁伤效果，很好地避开多层感知机模型的主要缺点也就是泛化性不足.同时，多层感知机模型的优势是容易得到较为精细的输入输出之间的映射关系，更容易胜任相关工作.基于上述分析，设计以2 维变量（炸高、落角）为输入的神经网络架构如图6 所示.

图6 神经网络架构示意图Fig.6 Neural network architecture

正向传播时，对于单个神经元：

对x进行线性操作得到z，再对z进行非线性操作得到a，当非线性操作为Sigmoid时，

反向传播时，采用梯度下降的方法：

式中：L为均方差损失函数；y(x)为真实数据，用学习率ƞ对w和b进行不断地迭代更新.具体实施过程中采用Adam 优化器，收敛速度更快，找到全局最优解的可能性更高.

训练集与测试集均通过第2 节中建立的毁伤效能评估模型产生.已知杀爆弹威力场与目标参数，设置不同落角与炸高参数，可得到大量毁伤效果图像用于模型训练，最终得到毁伤效果预测代理模型.代理模型与原模型计算条件与时耗如表1 所示（AMD R7 5800H 处理器3.20 GHz，VS2010 以及python3.9.12仿真环境）.由表1 可知代理模型可将原毁伤效能评估模型计算时耗由秒级缩短至毫秒级，故使用代理模型作为瞄准点分配模型中的评价函数，可将优化求解时耗由分钟级缩短至秒级，满足实际作战中对指挥决策的时间要求.

表1 神经网络模型与毁伤幅员模型性能对比Tab.1 Comparison between performances of neural network model and damage size model

4 算例分析

为考察本文方法的优越性，使用不同的方法对150 m×150 m 敌方轻装甲集群目标区域进行瞄准点规划，假定轻装甲车辆目标在打击区域内均匀分布，使用毁伤幅员作为打击毁伤效能评估指标.方法一采用传统考虑弹药毁伤半径的均匀分布式多点打击，方法二采用本文考虑弹药动爆威力的瞄准点分配方法.本次任务共装配6 发制导杀爆弹，其CEP 为10 m、落角80°、方位角0°、落速350 m/s、炸高8 m，如图7所示，弹药战斗部静爆威力场数据来自于有限元仿真软件Autodyn，破片共7 653 枚.仿真获取静爆威力数据作为毁伤效能分析模型输入参数，生成毁伤幅员预测代理模型参与瞄准点规划运算.

图7 Autodyn 战斗部静爆威力仿真示意图Fig.7 Simulation of warhead static explosion power through Autodyn

目标微元在长宽方向划分间距都为1 m，杀爆弹对轻装甲目标毁伤模式主要为通过破片侵彻毁伤，故目标微元毁伤律采用线性分布概率和有效破片密度准则，具体形式见式（5），可将轻型装甲车辆等效为13 mm 的厚装甲板[21]，其有效破片动能阈值为5 790 J[18]，毁伤判据Ɛth取3 枚/m2.

依照两种方法分配的瞄准点方案执行打击任务，造成毁伤区域对比如图8 所示，毁伤效果计算值对比见表2.

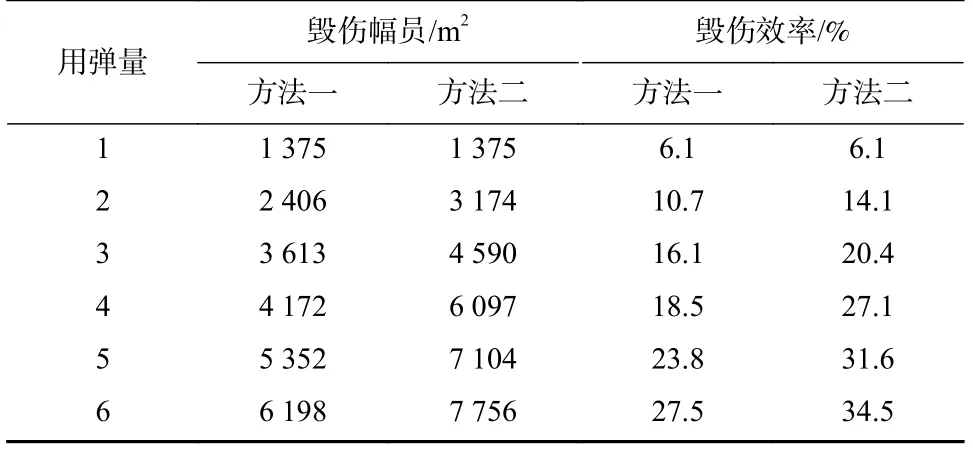
表2 两种打击方案对面目标毁伤效果Tab.2 Damage effect of two attack schemes on area target

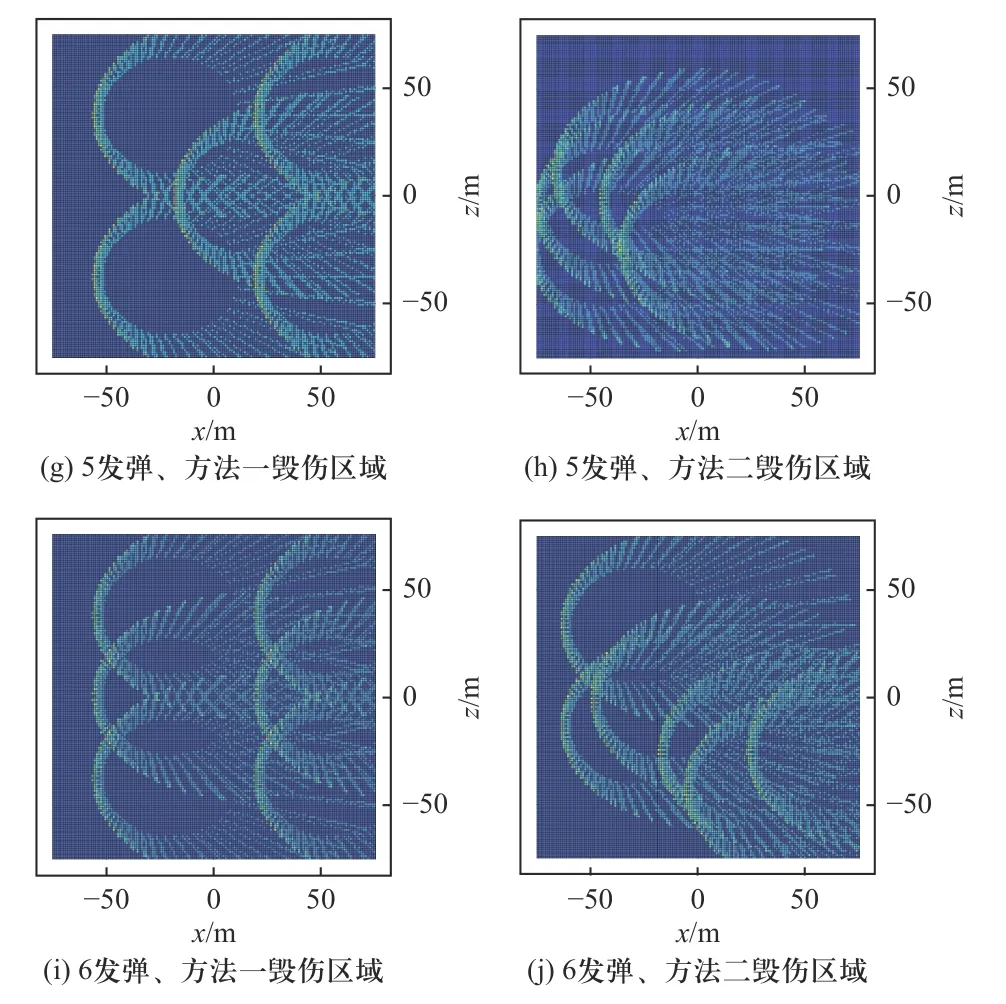
图8 两种打击方案对面目标毁伤区域Fig.8 Damage effect of two attack schemes on area target

两种方法在不同用弹量情况下对目标分配的瞄准点位置在目标坐标系下坐标值如表3 所示.

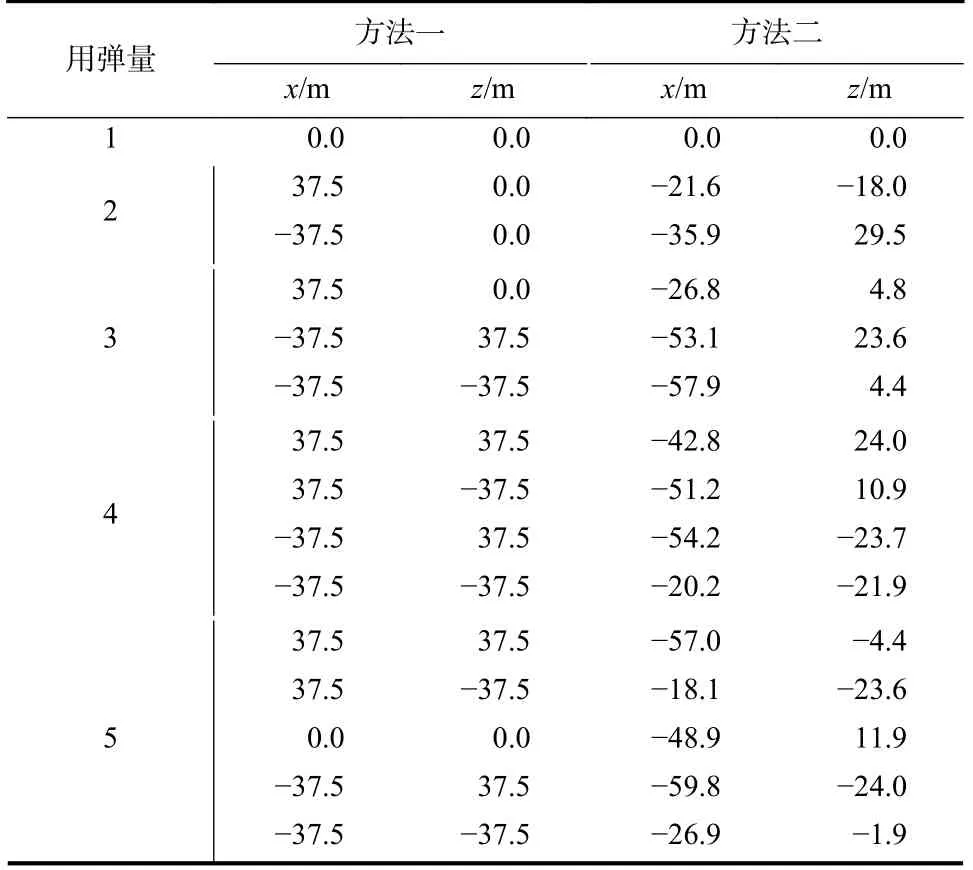
表3 不同用弹量下两种打击方案的瞄准点坐标Tab.3 Aiming point coordinates of two attack schemes with different ammunition consumptions

融入弹药动爆威力的瞄准点分配方法比传统方法打击面目标毁伤效率提高量和提高数据列于表4.

表4 考虑动爆威力的打击方案毁伤效率提高值Tab.4 Damage efficiency improvement value of attack scheme considering dynamic explosive power

5 结 论

①本文以杀爆弹动爆威力场与目标易损特性为基础，结合微元化思想建立了以毁伤幅员为效能表征量的融入杀爆弹动爆威力的毁伤效能分析模型，可实现多杀爆弹联合打击下对面目标毁伤效能分析.

②基于建立的效能分析模型，生成大量毁伤效能数据对神经网络模型进行训练，得到多杀爆弹联合打击下对面目标毁伤效能快速预测代理模型，在同样计算条件下，比非代理模型计算方法时间缩短至毫秒级，可用于缩短瞄准点规划模型计算时耗.

③ 建立了基于差分进化算法的多杀爆弹对面目标瞄准点规划模型，可针对多杀爆弹联合打击面目标情况下的每枚弹药的瞄准点和末端弹道参数以及引信参数进行规划，得到最优火力打击方案.

④采用算例对比分析表明：在计算时耗都可满足作战指挥需求条件下，与传统基于毁伤半径的多弹打击面目标瞄准点规划方法相比，毁伤效率大幅提高，最低可达25.5%.