低速撞击下PBX 炸药黏弹塑性细观损伤点火模型研究

2024-01-30王昕捷王心宇丁凯黄风雷

北京理工大学学报 2024年2期

王昕捷，王心宇，丁凯，黄风雷

（北京理工大学爆炸科学与技术国家重点实验室，北京 100081）

高聚物黏结炸药(polymer bonded explosives, PBX)是一种由炸药颗粒、黏结剂以及少量塑性剂组成的复合材料[1-2].在外部载荷作用下，炸药内部容易产生损伤形成热点，从而引起炸药的点火和起爆.产生热点的主要机制有孔洞塌缩、微裂纹摩擦、绝热剪切以及位错坍塌等，但由于PBX 炸药细观结构的复杂性，不同类型载荷作用下的损伤-点火机制仍难以确定.因此，研究外部刺激作用下炸药的力学、点火响应特性对于炸药安全性评估具有重要意义[3].

炸药安全性实验用于研究各类机械刺激对炸药点火起爆特性影响.这类刺激的作用时间较长、压力幅值不高，称为低幅值长脉冲载荷.在这类载荷作用下，炸药的黏塑性局域化往往对其“热点”形成过程影响显著.经典的SUSAN 试验[4]和STEVEN 试验[5]分别用于评价冲击挤压和撞击剪切作用下炸药的安全性.霍普金森杆实验[6]则主要研究应力平衡时炸药动态力学特性的温度及应变率效应.HOLMES等[7]通过自行设计的低速撞击装置，通过改变空气脉冲压力控制撞击速度对炸药进行加载，研究炸药典型区域的大变形及剪切破碎效应，并通过高速可见光摄像和红外成像测得了撞击过程中炸药的温度场以及热点温度.

由于目前实验细观表征技术仍不成熟，很多学者通过建立力化学耦合模型开展数值计算研究炸药的点火起爆机理.DIENES[8-9]对几种热点机制生成能量的量级进行比较，认为低幅值长脉冲冲击波作用下，炸药晶体内闭合的微裂纹摩擦生热效应是主要热点机制.BENNETT 等[10]在SCRAM 和Iso-SCRAM模型[11]的基础上建立了Visco-SCRAM 模型，该模型通过引入广义Maxwell 体，考虑了PBX 炸药的黏弹性力学响应，并简化了微裂纹摩擦热点模型.YANG等[12]在Visco-SCRAM 框架中基于主控裂纹概念[13]引入广义Griffith 失稳准则和孔洞坍塌及扭曲方程，提出了具备自适应能力的细观损伤热点模型.然而大多数模型只针对某一特定损伤点火机制，或仅适用于描述特定应力状态下炸药力学行为，不能描述复杂载荷作用下PBX 中黏塑性、微裂纹及微孔洞等多种相关物理机制共同存在和相互作用对炸药行为的影响，因此需发展适用于不同载荷条件且考虑多种力学变形、损伤热点机制的细观模型以正确描述PBX 炸药响应.

因此，本文通过引入微裂纹数量密度因子，考虑不同应力状态下的微裂纹尺寸及微裂纹数量密度演化规律，并对Bonder-Partom 黏塑性理论进行改进，发展基于非线性黏弹、黏塑及微裂纹、微孔洞细观损伤-热点机制的力化学耦合模型，并结合HOLMES等开展的PBX-9501 炸药低速撞击试验结果，数值研究PBX 炸药在此过程中的力学响应及细观点火机制.

1 微裂纹-微孔洞力化学耦合模型

1.1 黏弹塑性统计裂纹模型

黏弹塑性统计裂纹本构模型如图1 所示，由广义黏弹性体、微裂纹体以及考虑应变率硬化效应的塑性元件串联组成.

图1 黏弹塑性统计裂纹模型示意图Fig.1 Schematic diagram of viscoelastic plastic statistical crack model

广义Maxwell 黏弹性体由N个Maxwell 黏弹性体元组成，其中和分别为第n个Maxwell 体元中弹性元件的剪切模量和黏性元件的阻尼系数，下标s 表示压实的PBX 炸药；和分别为裂纹体的偏应力率和偏应变率；和分别为塑性元件的偏应力率和偏应变率.

根据广义黏弹性体元的并联特性，可以推出其偏应力率为：

PBX 炸药的塑性变形由改进的Bodner-Partom 模型描述，B-P 模型能表征如循环加卸载特征等一系列黏塑性变形的力学特性，其主要由3 部分组成，

由式(3)～(6)可得到，

微裂纹体本构关系为：

式中：c为微裂纹尺寸； βe与剪切模量和微裂纹数量密度Nc有关，满足2Gβe=ANc=，其中Nc的演化方程如下，

式中：Nt和Ns分别为拉伸和压缩条件下最大微裂纹数量密度； σt0、 τs0和 τs1分别为不同条件下微裂纹演化阈值；α和 α1均为材料参数.上式分别为主微裂纹处于纯张开、摩擦自锁和闭合-剪切状态.

微裂纹尺寸为c时，其能量释放率g可表示为

式中f(σ,n)为应力函数，由 σij与n共同决定.定义应力二轴度r（第三主应力与第一主应力比值），则不同应力状态下f(σ,n)为

式中各项分别表示主微裂纹处于纯张开、张开-剪切、闭合-剪切、纯剪切和摩擦自锁状态.微裂纹扩展速率可表示为

由式(1)(2)(7)(8)可得到，

含孔隙PBX 炸药的容变变形行为由p-α模型[14]描述，当压力超过孔洞临界弹性压力pe时，炸药中的孔隙逐渐塌缩，产生不可逆的塑性变形，当压力超过孔洞临界压实压力pc时，含孔隙PBX 炸药被完全压实.炸药中孔隙率f的演化可表示为

应力σij可分解为静水压力p和偏应力Sij两部分，静水压力p利用Mie-Grüneisen 状态方程代替，并结合上述偏应力的更新方法，更新下一时间步的应力.

1.2 宏观体积温升模型

式中：第一项为绝热压缩加热功率； Γ0为PBX 炸药的Grüneisen 系数；为体应变率； ℑ为非弹性功生热转化百分比；CV为定容比热；和分别表示黏性、塑性和裂纹脆性对应的非弹性功率；最后一项为化学反应生热速率，其中，Qr、Z、EA和R分别为单位质量化学反应放热、指前因子、活化能和理想气体常数.

1.3 微裂纹-微孔洞点火模型

1.3.1 微裂纹热点模型

微裂纹热点模型可用来描述微裂纹闭合面摩擦生热产生的热点，当微裂纹表面剪切驱动力大于静摩擦力时，微裂纹摩擦生热开始缓慢积累.微裂纹摩擦热点模型的温度求解由修正的Frank-Kamenetskii方程确定，

式中：Tc为微裂纹热点温度； µd为动摩擦因数；∂vx/∂y为沿裂纹表面的滑移速度；Tm为熔化温度；L为潜热；lf为微裂纹热点区域一侧的长度.由于摩擦生热，热点区域内部炸药与外部可能存在液相与固相的区别.在等式中，第1 项表示热点发生热传导的热量；第2项表示化学反应放出的热量；第3 项表示微裂纹内部的摩擦生热.

1.3.2 微孔洞热点模型

当PBX 炸药受到较高压力冲击加载时（高应力三轴度），微孔洞可能发生坍塌并在坍塌孔洞周围形成热点.细观尺度下微孔洞坍塌导致的黏塑性功生成速率可表示为

式中：b0为微孔洞的初始外径；为塑性体积应变[15-16]；ηc为材料黏性系数；右边2 项分别表示炸药的塑性与黏性效应所产生的功率.因此微孔洞热点温度Tvo可表示为

将微裂纹-微孔洞力化学耦合模型编写成材料用户自定义子程序，其计算流程图如图2 所示，表1～4 分别给出了PBX-9501 炸药的黏弹性参数、统计裂纹参数、塑性及孔洞相关参数和热力学参数[10,17-20].

表1 PBX-9501 炸药的黏弹性参数[10]Tab.1 Viscoelastic parameters of PBX-9501[10]

表2 PBX-9501 炸药的统计裂纹参数[21]Tab.2 Statistical crack parameters of PBX-9501[21]

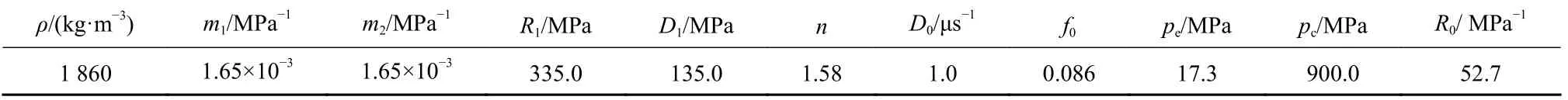
表3 PBX-9501 炸药的塑性及孔洞相关参数[19,22]Tab.3 Plasticity and pore related parameters of PBX-9501[19,22]

表4 PBX-9501 炸药的热力学参数[17]Tab.4 Thermodynamic parameters of PBX-9501[17]

图2 计算流程图Fig.2 Computational flow diagram

2 数值仿真

2.1 有限元模型

为研究低速撞击条件下炸药发生的破碎和剪切生热响应，开展PBX-9501 炸药低速撞击实验[7]有限元数值模拟.计算模型包含炸药试样、撞击柱以及刚性墙，炸药尺寸与实验保持一致（Φ6.35 mm×6.35 mm），网格尺寸为0.13 mm，共划分为84 239 个网格；撞击柱尺寸为Φ23.6 mm×84.7 mm，共划分为902 919 个网格.实验中炸药底部的固定支座为蓝宝石，由于蓝宝石的波阻抗远高于炸药，因此在模型中以刚性壁面替代，通过对撞击柱施加初始速度进行加载，建立的有限元模型如图3 所示.为分析炸药内部不同位置力学变形、损伤及点火情况，在药柱轴向中心处等间隔选取3 个代表性单元，用于分析各状态变量在药柱轴向的分布情况及其随时间演化情况.图4 为不同时刻炸药变形形貌与实验对比情况，在整个撞击过程中炸药变形呈现 “花瓶状”，头部变形程度比中部与底部位置更大，仿真结果与实验结果基本一致.

图3 PBX-9501 压溃数值仿真有限元模型图Fig.3 Finite element model of PBX-9501 crushing experiment

图4 炸药不同时刻炸药实验变形形貌(a)～(d)与仿真(e)～(h)图像对比Fig.4 Explosive deformation morphology (e)～(h) compared with experimental results (a)～(d)

3 计算结果及分析

3.1 炸药力学响应

图5 为撞击速度为59 m/s 时炸药轴向不同位置的应力历史及云图，当撞击柱撞击样品时，压缩波传入炸药内部，炸药应力开始增大.随着应力波的传播，由于黏塑性损伤耗散效应，其所能达到的应力峰值会逐渐减小，顶部应力水平最高，可达到122 MPa.当传播到炸药下表面时，钢壁面反射回炸药样品加载压缩波，此时底部位置的应力峰值相比中部位置更高.并且中部位置的炸药同时受到惯性约束作用，所以其位置应力较其他位置呈现显著减小趋势（～63 MPa）.同时在撞击过程中，试样需经历多次加载压缩作用，在15 μs 后，应力水平逐渐均匀，炸药各位置形变量基本一致，但由于撞击初期顶部应力较高，所以在整个撞击过程炸药变形呈现 “花瓶状”，顶部位置的侧向膨胀程度更高.在炸药的应变软化阶段，可发现其内部应力并未完全卸载到0，说明炸药发生大变形-破碎损伤之后，其仍具备一定的承载能力.

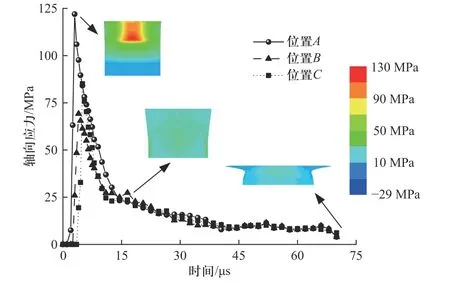
图5 撞击速度为59 m/s 时炸药轴向不同位置应力历史及云图Fig.5 Stress histories and contours at different axial positions of explosive at an impact velocity of 59 m/s

图6 为撞击速度为59 m/s 时炸药轴向不同位置单位体积塑性功历史及云图，对比应力曲线可知，在炸药内部应力达到峰值前，其塑性功也开始缓慢积累，在15 μs 时达到最大值，进入塑性流动平台阶段，同时塑性流动增强了材料的韧性.通过对比，炸药顶部位置的塑性功最大，可以达到4.05 MPa，呈现了明显的应变硬化现象，进而导致顶部位置所能达到的应力峰值更高.

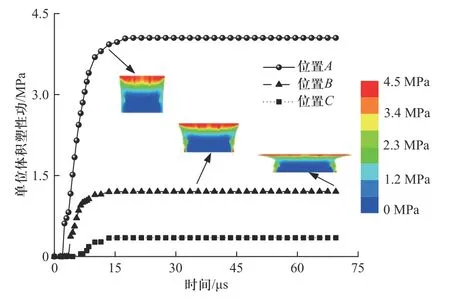
图6 撞击速度为59 m/s 时炸药轴向不同位置单位体积塑性功历史及云图Fig.6 Histories and contours of plastic work per unit volume at different axial positions of explosive at an impact velocity of 59 m/s

图7 为撞击速度为59 m/s 时炸药轴向不同位置处孔隙度f演化曲线，由图可知，随着应力波的传播，含孔洞炸药所受到的静水压力逐渐增大，孔洞发生不可恢复的塑性体应变，当静水压力达到峰值时，材料变为完全压实状态，之后，孔隙度f维持恒定.通过与图6 对比，在炸药开始发生塑性屈服时孔隙率开始减小，逐渐坍塌，微孔洞的坍塌在一定程度上也增强了其韧性，使得炸药在达到塑性流动平台段后，随着应力持续增加至最大值，孔隙率也坍塌到一个趋近于恒定的数值.可以看出顶部位置孔隙压塌程度更高，这是由于孔隙度仅与压力所能达到的峰值水平有关，可塌缩至0.068.

图7 撞击速度为59 m/s 时炸药轴向不同位置孔隙度历史及云图Fig.7 Porosity histories and contours at different axial positions of explosive at an impact velocity of 59 m/s

图8(a)为撞击速度为59 m/s 时炸药轴向不同位置微裂纹损伤度历史，由图可知，微裂纹首先处于摩擦自锁状态，随着应力波传播轴向应力增大，当微裂纹表面的剪切驱动力大于裂纹扩展所需的最大静摩擦力时，微裂纹开始进入发生失稳扩展的剪切摩擦区域.随后，在15 μs 左右炸药接近完全损伤.图8(b)为撞击速度为59 m/s 时不同时刻炸药微裂纹数量密度历史，由图可知，微裂纹首先增长，然后是裂纹数量密度稍晚增加，在7 ～20 μs（图中A点）时间段内，底部位置微裂纹数量密度较高，20 μs 之后顶部微裂纹密度演化速率加快，所达到的峰值水平更高.这是由于加载初期，顶部位置应力高，其微裂纹大多处于摩擦自锁状态，微裂纹无法形核或演化，而在20 μs之后，整个药柱应力水平幅值较低并趋于均匀，且顶部位置损伤程度一直处于较高水平，最终顶部位置微裂纹数量密度可达到53.94 cm-3.

图8 撞击速度为59 m/s 时炸药轴向不同位置的微裂纹损伤度和微裂纹数量密度历史Fig.8 Microcrack damage degree and density number histories at different axial positions of explosive at an impact velocity of 59 m/s

由于炸药内部应力及损伤存在着明显的不均匀性，所以在分析炸药宏观体积温度时，选取与实验测温相同区域内炸药表面单元取平均，得到如图9 所示的炸药宏观体积温度时间曲线.由图可知，在整个加载时间过程中宏观体积温度(Tbulk)变化主要受到裂纹功和绝热体积压缩功的影响，绝热体积压缩功和裂纹功对宏观体积温升影响相对较大，塑性功以及黏性功的影响相对较小.由于12 μs 之前宏观体积温升主要受到绝热压缩功的影响，所以二者的变化趋势基本一致，随着应力波传播到炸药内部，炸药首先发生弹性变形，弹性势能开始累积，绝热体积压缩功所导致的温度开始上升，同时随着孔隙率降低，炸药剪切模量增大，从而导致炸药抵抗变形的能力增大，绝热压缩温升增长速率变小，在12 μs 时达到最大.随着加载应力的升高，炸药微裂纹表面的剪应力逐渐增大，裂纹摩擦功开始缓慢积累，在炸药接近完全损伤后对温升起主导作用.由图可知，最高宏观体积温升为303.85 K，略高于实验所测得的宏观体积平均温度(302.3 K)，这是由模型中未考虑热传导效应导致的.

图9 撞击速度为59 m/s 时炸药宏观体积温度历史Fig.9 Bulk temperature histories of explosive at an impact velocity of 59 m/s

3.2 炸药点火响应

由于PBX 炸药内含能晶体与黏结剂分别具有脆性与韧性特征，其内部可能同时存在微裂纹、微孔洞两种初始缺陷.在低速撞击条件下，相应的损伤主导机制并不唯一，导致炸药发生点火的机制还不能确定.

图10 为撞击速度为59 m/s 时炸药轴向不同位置的最大剪应变率和微裂纹热点温度历史曲线，位置A选取微裂纹热点温度最高单元进行分析.从图中可以看出，整个加载过程中，炸药最大剪应变率存在着轴向的不均匀性，顶部位置的最大剪应变率始终较其他位置更大，在15 μs 时剪应变率达到第一次峰值0.29 μs-1，后出现震荡下降.通过前文对炸药损伤情况的分析可知，顶部位置率先发生失稳扩展，且扩展模式为剪切摩擦.由于剪切裂纹摩擦生热速率与其最大剪应变速率正相关，所以炸药形成微裂纹热点，进而诱发点火响应.当高度的应力集中使得微裂纹发生失稳扩展时，裂纹摩擦生热以及化学反应释放的热量会使得温度发生增长.

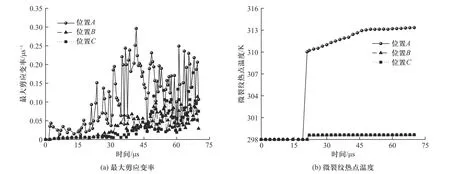
图10 撞击速度为59 m/s 时炸药轴向不同位置最大剪应变率及微裂纹热点温度历史Fig.10 Maximum shear strain rate and microcrack hot spot temperature histories at different axial positions of explosive at an impact velocity of 59 m/s

图11 和12 分别为炸药在不同时刻微裂纹热点温度云图与实验图像的对比，由图可知，15 μs 后炸药接近于完全损伤，微裂纹表面温度较高的区域主要集中在撞击柱与炸药撞击面边侧区域，进而在该区域内形成微裂纹热点（热点位置见图12）.数值仿真得到的热点温升为15.3 K，与实验结果基本一致.由研究可知，顶部位置处微裂纹率先发生失稳扩展，且扩展模式为剪切摩擦.由于剪切裂纹摩擦生热速率与其扩展速率正相关，顶部位置很有可能率先形成微裂纹热点，进而诱发点火响应.

图11 炸药不同时刻微裂纹热点温度侧视图云图与实验图像[7]对比Fig.11 Microcrack hot spot temperature contours of explosive compared with experimental results[7]

图12 炸药不同时刻微裂纹热点温度俯视图云图(e）～（h)与实验图像[7] (a）～（d)对比Fig.12 Microcrack hot spot temperature contours of explosive (e）～（h) compared with experimental results (a）～（d)[7]

根据微裂纹摩擦点火模型，计算出不同时刻裂纹空间温度分布如图13 所示，随着撞击柱的加载，累积的热量使得微裂纹面温度越来越高，最后在69 µs时，微裂纹中心温度达到了313.3 K.然而由于热传导作用，产生的热量沿微裂纹法向方向发生热传导，温度逐渐降低.可以发现，由于单位时间内微裂纹摩擦功产生的热量大于热传导所导致的热耗散，裂纹中心处的温度越高，单位距离温度梯度越大.

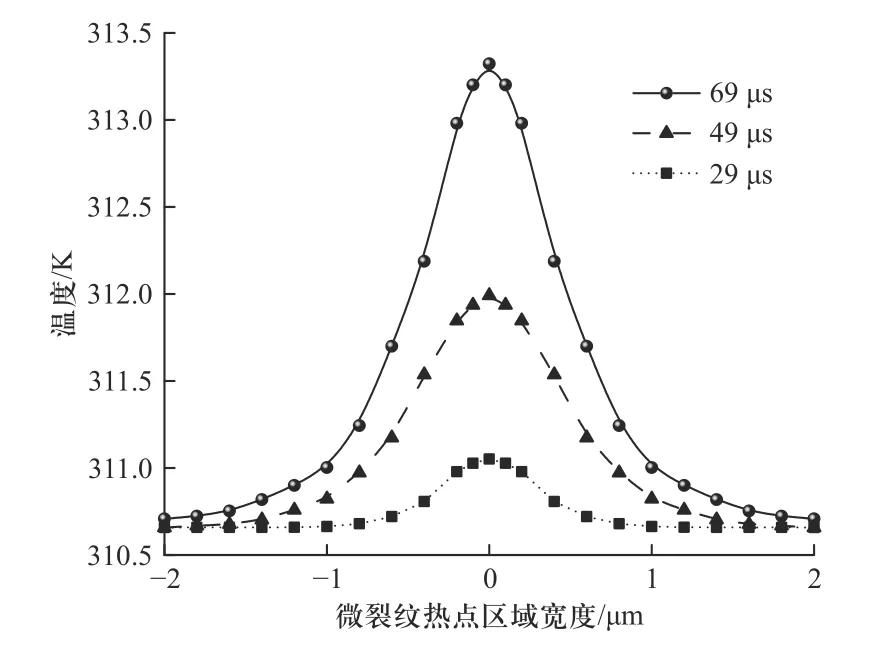
图13 撞击速度为59 m/s 时不同时刻裂纹空间温度分布图Fig.13 Temperature distribution in crack space at different times at an impact velocity of 59 m/s

为研究孔隙坍塌对热点形成的影响，图14 为撞击速度为59 m/s 时炸药轴向不同位置的微孔洞热点温度历史曲线.由图6 可以看出，随着应力波的传播，炸药轴向孔洞坍塌速率呈现明显的不均匀性，顶部位置孔洞坍塌速率快，而孔洞塌缩速率对于炸药黏塑性功的增加起着决定性的作用，由黏塑性变形耗散功以及化学反应生热两部分引起的热累积远小于对应的热耗散，使得Tvo数值上升不显著.可以看出，顶部位置孔隙率最高塌缩到0.068，微孔洞温度出现较小温升，仅能达到303.7 K.

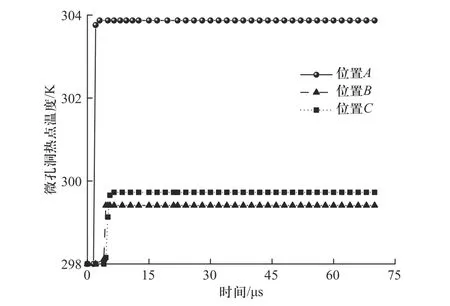
图14 撞击速度为59 m/s 时炸药轴向不同位置的微孔洞热点温度历史Fig.14 Microvoid hot spot temperature histories at different axial positions of explosive at an impact velocity of 59 m/s

图15 为炸药宏观体积温度温度Tbulk、剪切裂纹摩擦热点温度Tc以及孔洞坍塌热点温度Tvo对于点火响应的影响对比图.在20 μs 后，Tc的增长速率要远大于Tvo，因此该阶段内Tc变化对Tbulk的增大起主导作用.由图可知，Tc温度在微裂纹区发生失稳扩展时发生陡升.综上所述，低速撞击时微裂纹热点机制对炸药点火起主导作用.炸药的宏观体积温升小于微裂纹热点温度，炸药微裂纹热点表面温度达到313.3 K，而其整体温度仅为304.6 K，这体现出宏观与细观两个空间尺度温度变化的差异.整体温升即局部热点区域的背景温度，较高的背景温度会减少裂纹中心由于热传导所损失的热量，进而促进微裂纹中心温度的升高，所以随着撞击强度的增大，炸药宏观体积生热机制对于材料点火行为的影响变得越来越重要.

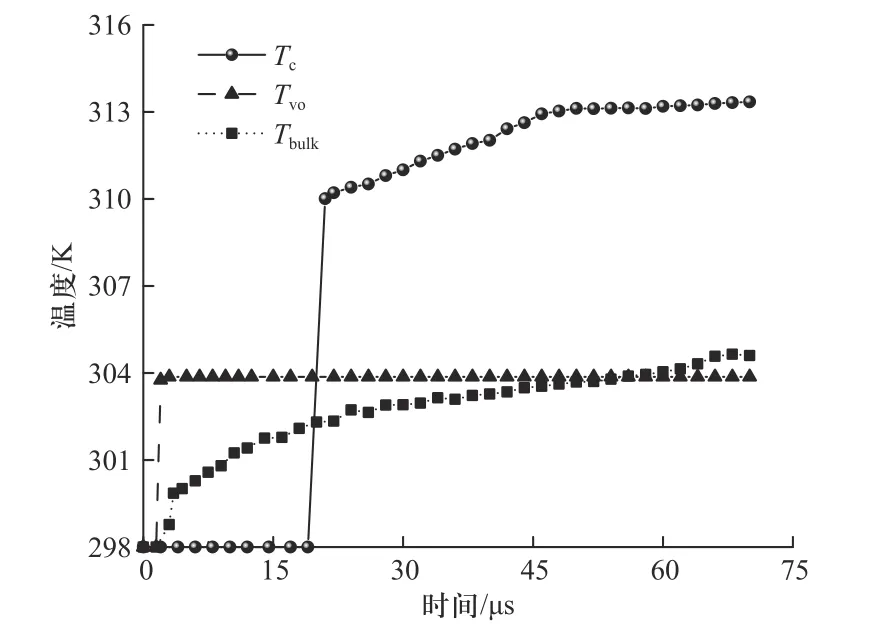
图15 撞击速度为59 m/s 时顶部位置炸药宏观体积温度Tbulk、裂纹摩擦热点温度Tc 以及孔洞坍塌热点温度Tvo 对比Fig.15 Comparison of bulk temperature Tbulk, microcrack hot spot temperature Tc and microvoid hot spot temperature Tvo at an impact velocity of 59 m/s

撞击速度会影响炸药的热点形成过程，因此通过改变撞击柱的撞击速度预测PBX-9501 炸药临界点火速度阈值对于评价炸药撞击感度具有重要意义.如图16 所示为不同撞击速度下(80、100、120、125、140、160 m/s)炸药温度最高代表性单元微裂纹和微孔洞热点温度演化曲线.由图可知，当顶部位置处受到初始撞击后，材料内部微裂纹发生快速失稳扩展，微裂纹表面摩擦生热会使得其表面温度快速升高.当撞击速度较低时(80～120 m/s)，微裂纹表面温度快速增长至峰值，随后由于热传导作用逐渐降低，如100 m/s 撞击速度下，微裂纹表面温度在45 μs 时达到峰值515 K.当撞击速度增加至125 m/s 时，炸药最大剪应变率随之增加，微裂纹表面温度持续增加至熔点时形成平台，对应于材料局部的熔化过程.当微裂纹表面发生完全熔化后，裂纹摩擦做功以及化学反应生热两部分引起的热累积使得温度发生第二次增长，进而使得Tc数值不断持续升高并最终发生热失稳，由图中微裂纹温度曲线的热失稳特征可确定点火临界撞击速度为120～125 m/s.对比图16(b)可以看出微裂纹温度始终高于微孔洞温度，压力升高导致的微孔洞塌缩所产生的黏塑性功生热不足以使得温度达到热失稳状态，在160 m/s 撞击速度下，随着孔隙度坍塌至一定值后温度仅能达到350 K.

图16 不同撞击速度下炸药微裂纹热点温度和微孔洞热点温度历史Fig.16 Microcrack hot spot temperature histories and microvoid hot spot temperature histories of explosive at different impact velocity