基于PSO 算法的半球谐振陀螺惯导系统陀螺温度补偿方法
2024-01-30董铭涛班镜超刘晓庆王胜兰
董铭涛,班镜超,刘晓庆,王胜兰,夏 旭
(湖南航天机电设备与特种材料研究所,长沙 410205)
0 引言
半球谐振陀螺(hemispherical resonator gyro,HRG)是一种新型哥氏振动陀螺,具有高精度、高可靠性、极为优异的SWaP(size,weight and power)特性以及抗辐照等优点[1-3]。半球谐振陀螺的核心部件为半球谐振子,由高纯熔融石英材料制成。在陀螺正常工作时,外部温度变化和谐振子振动发热会引起温度变化,导致半球谐振子的杨氏模量、密度、半径等参数发生变化,影响陀螺输出精度,温度漂移制约了半球谐振陀螺精度提升。已有研究成果表明,温度漂移误差是制约半球谐振陀螺精度提升的关键要素[4]。
通常,抑制半球谐振陀螺温度漂移的方法有温度稳定法和温度补偿法[5]。温度稳定法是增加外部温控系统,维持半球谐振陀螺温度保持恒定,使陀螺工作在恒温环境,减小陀螺温度漂移。其缺点为增加了系统体积和质量,并且由于谐振子处于真空环境,热传递仅依赖热辐射和支撑杆的热传递,稳定时间较长。该方法常在航天卫星系统中应用[6-7]。温度补偿法是根据半球谐振陀螺随温度变化的输出特性,建立温度变化的数学模型,通过软件补偿温度变化引起的温度漂移,具有不增加系统硬件结构同时提高陀螺精度的优点。
为提高半球谐振陀螺精度,科研工作者在温度补偿法方面做了大量工作。Wang等[8]利用谐振子可以作为一个高精度温度传感器的特点,对单陀螺开展多个温度点下的温度-频率标定试验,以温箱温度为基准,利用最小二乘拟合方法获取温度-频率函数的系数,同时,利用逐步线性回归的方法,建立以谐振子谐振频率为自变量、陀螺零偏为因变量的温度补偿模型,提高了半球谐振陀螺在大温度范围内的使用精度。以温箱温度为基准建立温度-频率函数的方法,适用于单一陀螺,而利用逐步线性回归方法建立温度补偿模型,仅通过多次试验方法确定模型阶次,具有一定的不可变性。
赵建宇等[9]将半球谐振子温度变化理解为一阶惯性环节,建立陀螺输出零偏随谐振子温度变化的数学模型,利用遗传算法优化BP 神经网络补偿温度漂移。然而,陀螺零偏与半球谐振子温度变化并非严格的一次关系,还需要深入完善设计数学模型,同时,仅考虑了温度变化并未考虑温度变化率的影响。李广胜等[10]根据温度变化和温度变化率间的相关性,建立半球谐振陀螺温度漂移的多项式数学模型,利用多项式拟合法确定模型最高次数为6,增加了温度求解的计算量。吴宗收等[11]将半球谐振陀螺温度漂移误差分为确定性误差和不确定性误差,在补偿确定性误差的基础上,利用改进PSOARMA(particle swarm optimization-autoregressive moving average model)方法补偿不确定性误差。对于确定性误差,并未考虑温度变化二次项的影响。
针对现有半球谐振陀螺温度补偿法存在的不足,提出一种基于粒子群优化(particle swarm optimization,PSO)算法的温度补偿方法。首先,以HRG 惯导系统中陀螺外侧测温电路温度为基准,引入逆向拟合思想,提出一种基于谐振频率的半球谐振陀螺温度输出方法;其次,建立温度补偿模型,考虑模型具有非线性特点,引入PSO 算法求解模型系数;最后,开展温度试验,验证算法的有效性。
1 HRG 惯导系统温度补偿方法总方案
以某国产力平衡式HRG 为基础搭建惯导系统,研究HRG 温度补偿方法,总体方案如图1 所示。力平衡模式也称为闭环检测模式,工作原理为:当HRG 旋转时,半球谐振子上的驻波相对HRG 壳体开始进动,通过力反馈控制回路对半球谐振子施加反馈力进行激励,使驻波克服科里奥利力效应与HRG 壳体实时保持一致,根据半球谐振子的反馈力计算HRG 的理论旋转角速度。
在图1中,HRG 惯导系统能同时输出陀螺信息和谐振频率信息。首先,开展多组温度试验获取不同温箱温度点下的HRG 谐振频率值、测温电路温度值。在此基础上,以测温电路温度为基准,建立温度-频率模型。引入逆向拟合思想,解决由谐振频率求解陀螺温度值时,需要实时求解一元三次方程,导致上位机解算负担大、无法实时输出温度的问题。获得HRG 温度输出模型,替代了传统陀螺测温电路。其次,在HRG 温度模型基础上,以温度变化、温度变化率及两者交叉项为自变量,以陀螺输出零偏为因变量,建立半球谐振陀螺温度补偿模型。根据HRG 陀螺输出值,引入PSO 算法求解温度补偿模型的模型系数,补偿由温度引起的HRG零位漂移。
2 基于谐振频率的HRG 温度输出方法研究
Wang等[8]针对单陀螺开展温度-频率标定试验,以温箱温度为基准,求解温度与谐振频率的函数,为陀螺温度补偿作铺垫。在实际应用中,通常将三只HRG装配组成惯导系统,用于测量载体的角速度进而实现导航功能,适用于单陀螺的以温箱温度为基准求解温度-频率函数的方法,未必适用HRG 惯导系统。因此,利用带温箱三轴转台,开展HRG 惯导系统温度试验,研究半球谐振陀螺温度输出方法。
在温度试验中,除了获取温箱温度外,还在HRG 金属壳体外侧粘贴测温电路(温度传感器为DS18B20,测温精度为0.062 5 ℃),测量陀螺壳体处温度。试验方案如下:温箱温度范围为-40~50 ℃,每10 ℃一个温度点,依次递推。在每个温度点下,先将温箱保温5 h,获得第5 h谐振频率值和测温电路温度值。
统计试验结果,如表1所示。表1中列出了在各温箱温度点(简称T1)下的三只陀螺第5 h的谐振频率值和测温电路温度值(简称T2),谐振频率值和测温电路温度值都为百秒平滑结果。
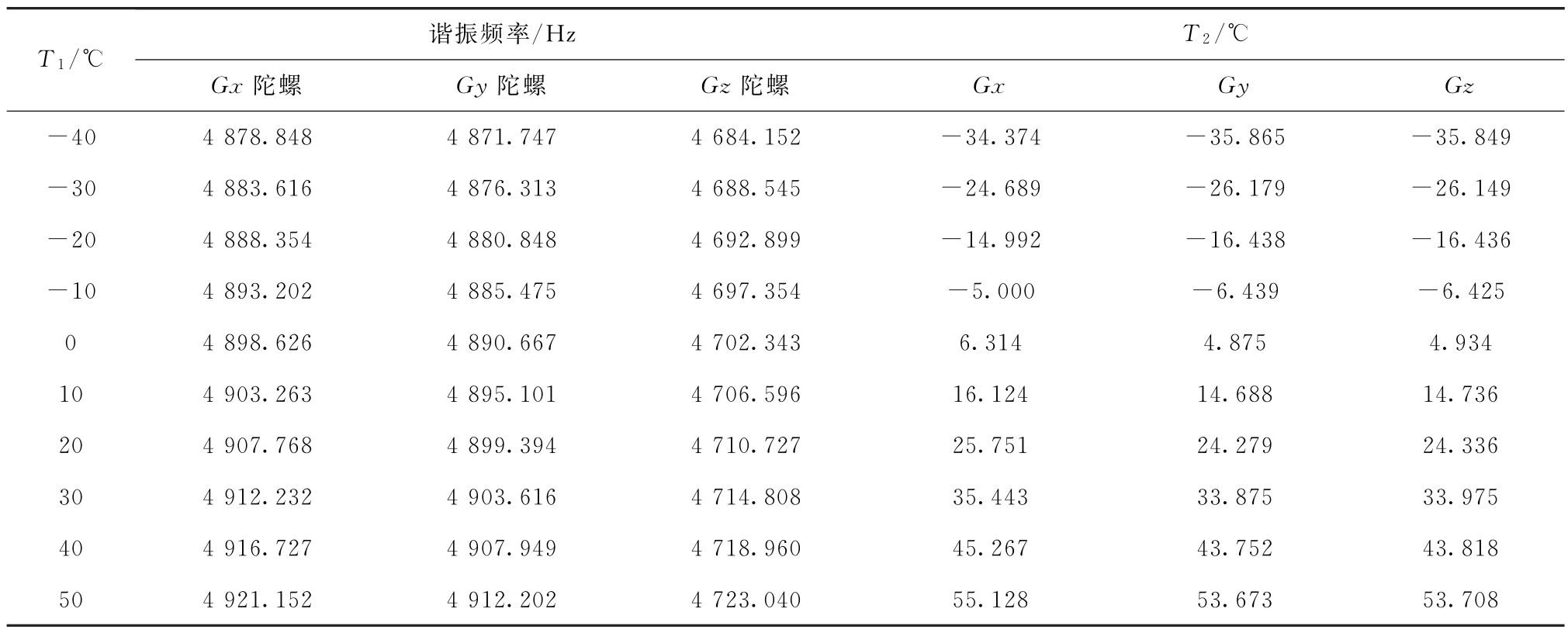
表1 各陀螺谐振频率和T 2Tab.1 The natural frequency and the T 2 of each gyros
2.1 以测温电路温度为基准的HRG 温度-频率方法
(1)以温箱温度T1为基准
在Wang等[8]温度-频率标定方法基础上,以T1为基准,求解HRG 温度-频率模型。以Gx陀螺为例,说明以T1为基准的温度-频率标定方法,Gy和Gz陀螺分析方法类似。利用最小二乘法获得拟合系数,得到温度-频率函数f1(T)为
由式(1)可知,三阶和二阶温度-频率系数非常小,温度与谐振频率之间不是严格意义的线性关系。根据谐振频率值将式(1)转换为一元三次方程,通常利用Matlab软件roots函数求解方程获得温度值(简称T3),将T3与T1作差并画图,如图2所示。
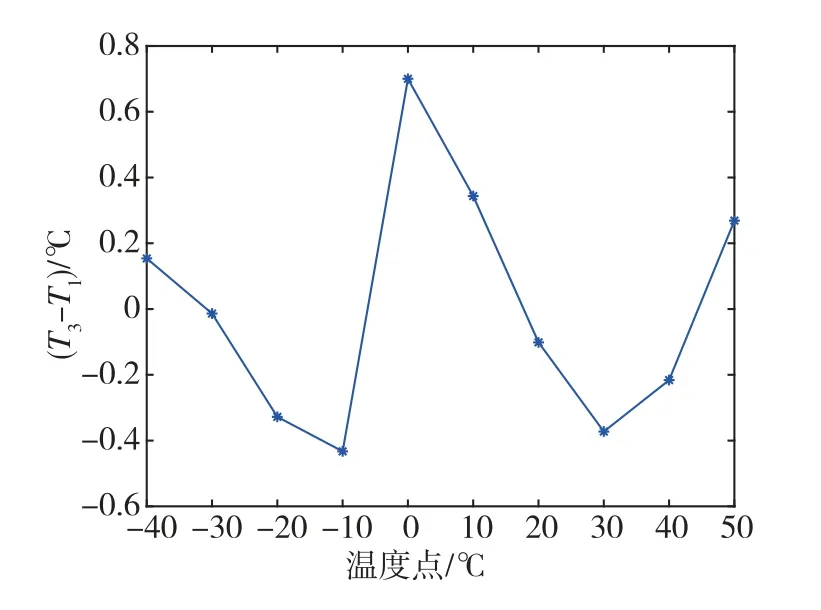
图2 T 3 与T 1 差值Fig.2 Difference between T 3 and T 1
由图2可知,根据Gx陀螺谐振频率解算的T3与对应的T1相差最大值为0.7 ℃左右,此时温箱温度为0 ℃;还有多个温箱温度点的温度差值超过0.1 ℃,与文献[8]中以温箱温度为基准时,温度精度优于0.1 ℃的结论不一致。因此,以温箱温度为基准求解温度-频率函数的方法,不能用于获得HRG 惯导系统的温度-频率函数。
(2)以测温电路温度T2为基准
同样以Gx陀螺为例,以测温电路温度T2为基准的温度-频率函数f2(T)为
在式(2)基础上,由各个谐振频率值解算得到T3,将T3与T2作差并画图,如图3所示。
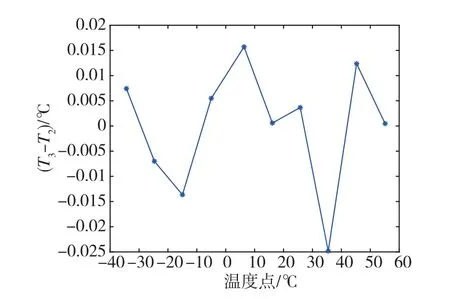
图3 T 3 与T 2 差值Fig.3 Difference between T 3 and T 2
由图3可知,在各个谐振频率值下,以式(2)解算的温度值与测温电路温度的差值未超过0.1 ℃,满足文献[8]中的温度精度判断方法。上述分析说明,测温电路更加靠近陀螺,测得的温度更接近陀螺真实温度。因此,在HRG 惯导系统中,需要以测温电路为基准求解温度-频率函数。
2.2 基于逆向拟合的HRG 温度输出方法
为了实时获取陀螺温度,将陀螺输出谐振频率值代入f2(T)函数,将式(2)中函数转变为一元三次方程,利用Matlab软件的roots函数实时解方程求解温度。在测试过程中,由于上位机需要实时调用Matlab软件求解方程,增加了上位机运算负担,影响陀螺温度输出实时性,在工程应用中难以大范围推广。在式(2)基础上,将温度范围扩展至-100~100 ℃,绘制温度-频率函数曲线,如图4所示。
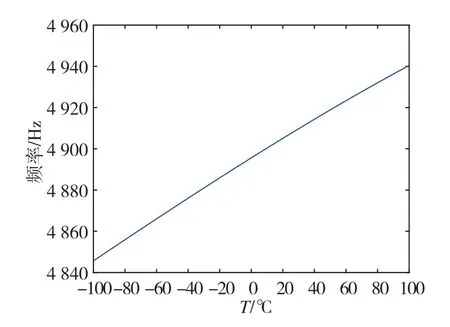
图4 温度-频率曲线Fig.4 Temperature-frequency curve
由图4中曲线可知,温度与谐振频率值之间具有一一对应关系,但不是严格意义的线性关系(二阶系数和三阶系数非零)。针对上位机实时解算一元三次方程对采集电脑性能要求高的问题,利用温度与谐振频率值之间一一对应的特点,引入逆向拟合思想,即求解频率-温度函数,由谐振频率值实时计算温度值,减小上位机计算量,提高解算效率和陀螺温度输出实时性。
因此,HRG 频率-温度函数通式为:T(fs)=afs3+bfs2+cfs+d。以Gx陀螺为例,求解频率-温度函数系数为:a=1.792×10-5,b= -2.608×10-1,c=1.267×103,d= -2.056×106。绘制Gx陀螺频率-温度曲线,如图5所示。

图5 Gx 陀螺频率-温度曲线Fig.5 Frequency-temperature curve of the Gx gyro
将求解温度-频率函数的过程记为正向解算,将求解频率-温度函数的过程记为逆向解算。统计正向解算温度(即T3)、逆向解算温度(简称T4)以及与T2间的差值,如表2所示。

表2 三种温度对比Tab.2 Comparison of three temperatures
由表2中结果可知,各谐振频率点对应的T4与T2的差值都未超过0.1 ℃,满足文献[8]中的温度精度判断方法。上述分析结果表明,逆向解算方法具有可行性,解决了正向解算时上位机运算负担大的问题,能够支撑半球谐振陀螺实时输出温度值。同时,基于谐振频率的半球谐振陀螺温度输出方法替代了传统的陀螺测温硬件电路,可为惯导系统轻小型设计提供新思路。
3 基于PSO算法的HRG温度补偿方法研究
前文指出,温度漂移是制约半球谐振陀螺精度提升的关键要素,通常利用温度补偿法补偿温度漂移的影响。要想补偿陀螺温度漂移,首先需要建立半球谐振陀螺温度补偿模型;其次,求解温度补偿模型系数。
3.1 HRG 温度补偿模型
半球谐振陀螺在工作过程中,谐振子振动会产生热量以及受环境温度影响,导致陀螺的热场具有不确定性或者出现非均匀性温度传导。建立半球谐振陀螺温度补偿模型时,除了考虑温度变化外,还需要考虑温度变化率。
在力平衡模式下,陀螺零偏b0由谐振子的振幅A0、阻尼不均匀、耗散角θτ、频率ω0等参数决定[6],即
若θτ较小时,将式(3)改写为
式中,γ1和γ2为温度系数,ΔT为温度变化率。因此,陀螺零偏b0为温度变化率的二次函数。
借鉴文献[8]中零偏补偿模型设计经验,考虑温度变化、温度变化率及两者交叉项,温度变化率最高次数为2,以及温度变化最高次数也为2,设计半球谐振陀螺温度补偿模型为
式中,k0为与温度无关的陀螺零偏值,T为温度值,ΔT/Δt为温度变化率,B为陀螺零偏,k1~k5为温度系数。
3.2 基于PSO 算法的温度补偿方法
熔融石英材料对温度较为敏感,半球谐振子工作时处于振动状态,HRG 输出信息具有较强的非线性[12],同时由式(7)可知,温度补偿模型具有非线性,传统的拟合方法不能准确地求解模型系数。借鉴其他文献经验,引入PSO 算法[13-14],求解温度补偿模型的模型系数。
PSO 算法是一种群体智能计算算法,借鉴鸟类捕食经验,使得粒子群快速收敛于全局最优解[15]。PSO 算法主要思想为:假定每个粒子表示温度补偿模型的一组系数,将粒子代入温度补偿模型获取适应度值;粒子具有带方向的速度值和带方向的距离值,通过粒子间的合作与竞争,在解空间中跟随最优粒子不断迭代寻找全局最优解。
在PSO 算法基础上,基于PSO 算法的温度补偿算法步骤如下。
步骤1:参数设置和粒子群初始化。
在标准PSO 算法基础上,开展大量仿真试验确定算法参数。选择粒子群规模为N=200,粒子维数D=6,为温度补偿模型待辨识系数个数;粒子位置范围为[-1,1],粒子速度范围为[-1,1];最大迭代次数为200,迭代次数影响算法运行时间和模型系数的精度;学习因子c1=c2=1.5,惯性权重w=0.8,表明算法具有更快的收敛速度。粒子群初始化含义为根据设置的参数值生成一组均匀分布在寻优空间中的随机值。
步骤2:计算初始化个体最优值。
计算个体最优值前,需要先确定适应度函数。在式(7)基础上,温度补偿模型的适应度函数为
式中,fitness为适应度值;bg(i)为实际陀螺零偏值;B(i)为温度补偿模型值;n为数据总长度,陀螺零偏值为陀螺输出除标度因数。根据初始化粒子确定粒子群中最优个体值P1best,为算法迭代开始前的最优个体。
步骤3:更新位置和速度值。
在算法迭代过程中,根据粒子最优值更新粒子的速度和位置,计算公式为
式中,w为惯性权重,c1和c2为学习因子,r1和r2为随机函数rand,生成0到1之间的随机数,Pk为局部最优值,为全局最优值,Xk为当前粒子位置值,k=1,2,3,…,N。
步骤4:更新个体最优值。
根据粒子群中的位置更新值计算粒子适应度值,并与前一次迭代的最优个体比较。若优于最优个体,则该粒子作为下一次迭代的参考个体,并将最优个体更新为当前个体。
步骤5:算法迭代。
不断重复步骤3和步骤4,当满足迭代终止条件时,此时粒子值便为温度补偿模型的最优解。
4 试验验证与结果分析
以某国产力平衡式半球谐振陀螺惯导系统为例,利用带温箱转台开展温度试验,三轴方向按北上东放置,惯导系统和温箱保持静止,使得半球谐振陀螺仅受地球自转激励,采用第2章所提方法实时采集半球谐振陀螺温度,某次试验照片如图6所示。常温环境下,该惯导系统通电5 h后,测得单陀螺精度为0.3(°)/h。

图6 HRG 惯导系统温度试验照片Fig.6 Temperature tests photo of HRG inertial navigation system
温度试验条件如下:从室温开始降温,降温时温箱选择设置温度点降温模式,待温箱达到-40 ℃后,保温5 h;达到保温时间后,以1 ℃/min开始升温,待三只陀螺温度都达到50℃后,结束温度试验。相同条件下,进行多次试验,并以某次试验为例说明。绘制Gz陀螺温度曲线及原始陀螺输出曲线如图7所示,温度值为百秒平滑结果。
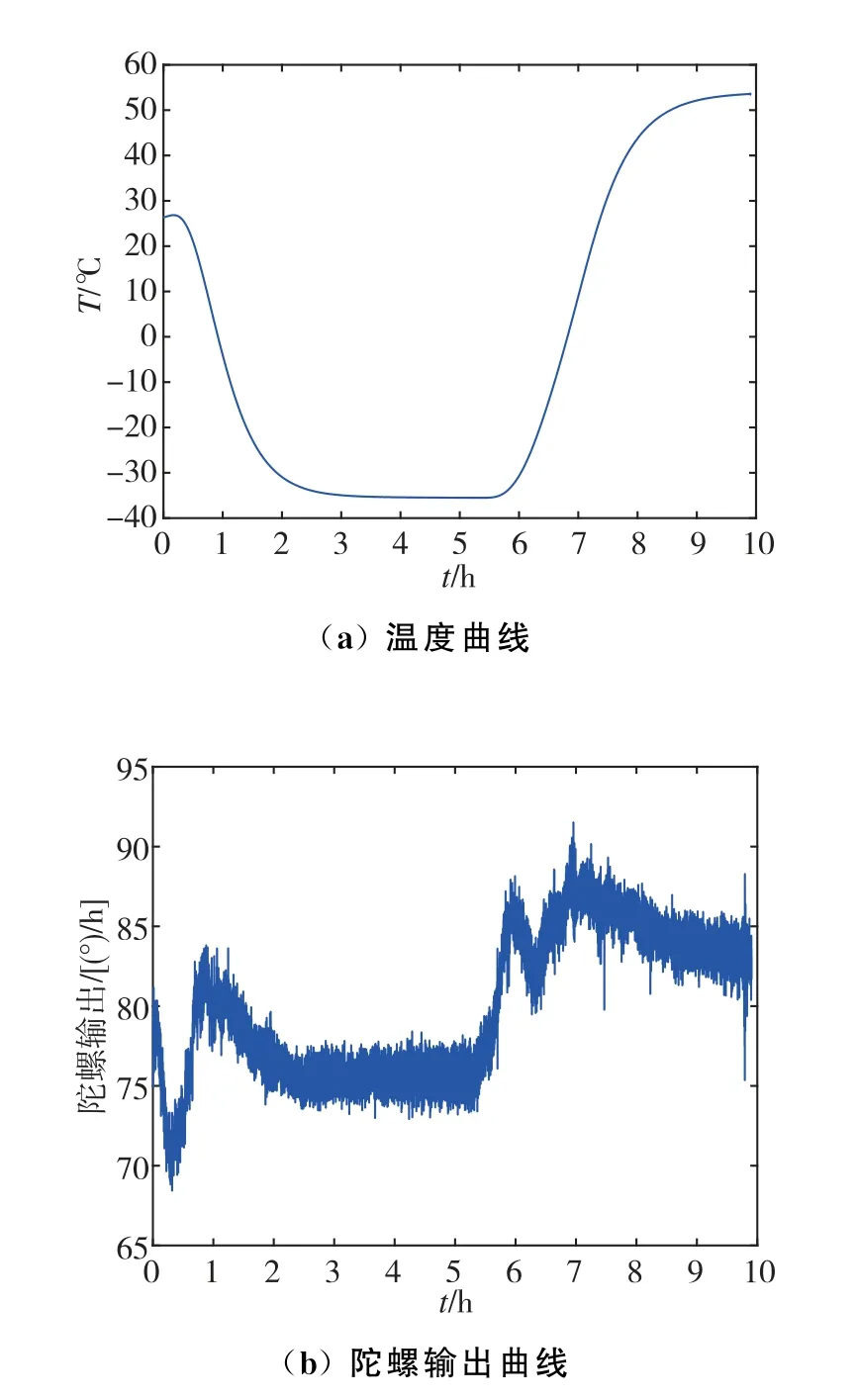
图7 Gz 陀螺曲线Fig.7 Curve of Gz gyro
由图7可知,温度试验包含降温阶段和升温阶段,在两个阶段中温度变化速率不同,可验证不同温度变化率对温度补偿模型的影响。因此,将温度试验划分为两个阶段分析,从图7中能够看出陀螺输出随温度变化。利用第3章方法分别求得降温阶段和升温阶段的温度补偿模型系数,如表3所示。

表3 温度补偿模型系数Tab.3 Coefficients of temperature compensation model
为了验证本文算法有效性,将本文算法与最小二乘法对比,绘制两个阶段的原始陀螺输出、PSO算法补偿后陀螺输出和最小二乘法补偿后陀螺输出的零偏曲线,如图8所示。为了便于对比原始陀螺输出与补偿后陀螺输出,将原始陀螺输出减去均值再画图。

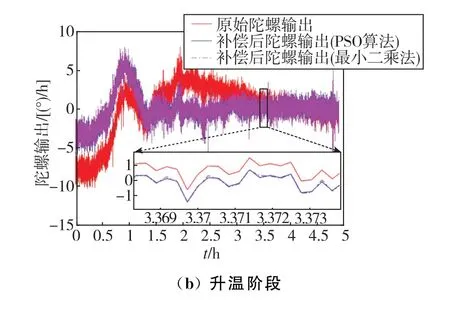
图8 陀螺输出曲线Fig.8 The gyro output curve
由图8中曲线可知,在温度大范围变化后,陀螺输出变化较大,利用本文算法补偿后陀螺输出变化减小很多。在HRG 惯导系统稳定后,经本文算法补偿后,陀螺输出被拉平,维持在0附近。在图8中,0~1 h曲线内出现陀螺输出剧烈抖动现象,主要原因为在温变条件下陀螺输出受影响,陀螺控制电路的控制参数还需要进一步完善。
计算原始陀螺输出、PSO 算法补偿后和最小二乘法补偿后的陀螺零偏稳定性,如表4所示,单位为(°)/h(3σ)。
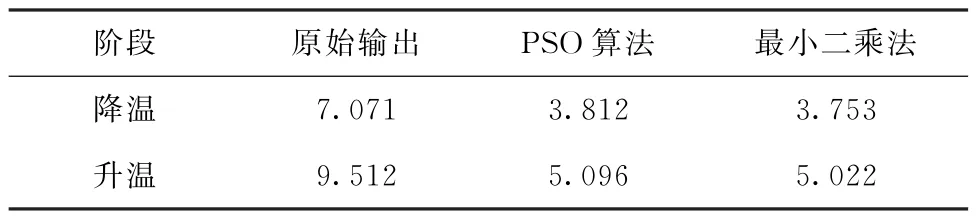
表4 零偏稳定性对比Tab.4 Comparison of bias stability(°)/h
由表4中统计结果可知,相比于温度补偿前,降温阶段零偏稳定性从7.071(°)/h改善至3.812(°)/h,优化46%;升温阶段零偏稳定性从9.512(°)/h改善至5.096(°)/h,优化46%。本文算法与最小二乘法补偿后结果相比较,零偏稳定性值差别不大,进一步验证了本文算法的有效性。上述分析结果表明,本文算法具有有效性,可以有效改善大温度范围内HRG 惯导系统陀螺输出随温度漂移的现象。
5 结论
本文设计了一种基于谐振频率的半球谐振陀螺温度输出方法,考虑温度变化、温度变化率以及两者交叉项,建立了HRG 惯导系统陀螺温度补偿模型,提出了一种基于PSO 算法的温度补偿方法。试验结果表明,本文算法在-40~50 ℃内能够降低HRG 温度漂移,补偿后的零偏稳定性较补偿前提升了46%,具有较好的工程应用价值和应用广泛性。
未来,可在以下几个方向开展技术研究:1)本文选用的HRG 属于中低精度陀螺,有待在更高精度HRG 惯导系统中验证;2)建立陀螺输出与谐振频率之间的数学模型,减少由谐振频率解算温度引起的误差;3)将PSO 算法与其他智能算法融合,提高智能算法性能和HRG 惯导系统陀螺零偏精度。
