两个等长圈的卡氏积的群超幻标号*

谢子康,邓贵新

(南宁师范大学 数学与统计学院,广西 南宁 530100)

1 问题背景

本文中的图都是有限简单图.图G的顶点集和边集分别记为V(G)和E(G),G中顶点x的点邻域N(x)和边邻域E(x)分别表示关联x的顶点的全体和关联x的边的全体.对正整数n≥3,用Cn表示含有n个顶点的圈,用n表示n阶循环群.交换群A的指数记为exp(A).图G1与G2的卡氏积,记作G1□G2,是以V(G1)×V(G2)为顶点集,且两个顶点(x1,y1)与(x2,y2)相邻当且仅当x1=x2且y1y2∈E(G2),或x1x2∈E(G1)且y1=y2.

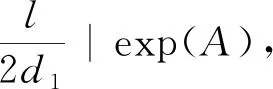
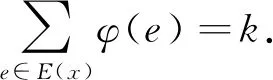
由定义1.2马上得到,如果G是超幻图,则G是n-超幻图,其中n=|E(G)|.文献[7]利用的结果证明了对任意正整数m,n≥3,Cn□Cm是2nm-超幻图.Froncek等[8]用统一的构造方式重新证明了该结论.很自然地,我们考虑哪些2nm阶交换群A使得Cn□Cm是A-超幻图.本文证明了对任意正整数n≥3及任意2n2阶交换群A,Cn□Cn都是A-超幻图.

2 主要结果

引理2.1[3]设A是有限交换群,H是A的一个指数为2n的子群(n为正整数),则存在xi,yi,c∈A,xi+yi=c,0≤i≤n-1,使得

定理2.2对任意正整数n≥3和任一2n2阶交换群A,Cn□Cn都是A-超幻图.

由有限交换群的结构定理可知A必有n阶子群.任取A的一个n阶子群H={h0,h1,…,hn-1},则由引理2.1,存在xi,yi,c∈A,xi+yi=c,0≤i≤n-1,使得

为叙述简便,以下x,y,h的下标以及顶点(i,j)的分量都模n计算.

情形1n是偶数.定义映射φ:E→A如下:

其中0≤i,j≤n-1.那么(i,j)关联的水平边的标号和为

而(i,j)关联的竖直边的标号和为

所以与 (i,j)关联的所有边上的标号和为

还需证明φ是双射.对每个i,显然有

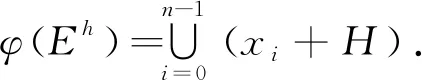
故有

这表明φ是从E=Eh∪Ev到A的满射.又因为|E|=|A|=2n2,故φ是双射.

情形2n是奇数.定义ψ:E→A如下:

对于(i,j)∈V,其关联的水平边的标号和为

而(i,j)关联的竖直边的标号和为

从而有

还需要证明ψ是双射.由n是奇数知,对任意r,s,存在整数i1,j1和i2,j2满足同余式