基于机理模型与深度学习的密炼工艺预测控制方法

2024-01-27关瑞琦苏永清白雪杨崔哲昕

自动化与仪表 2024年1期

关瑞琦，苏永清，白雪杨，崔哲昕

（同济大学电子与信息工程学院，上海 201804）

密炼是轮胎生产的必要环节，密炼过程的目的是得到流变性能适宜、门尼粘度合格的混炼胶，混炼胶的质量决定着后续加工和轮胎成品的质量[1]。模型预测控制已在工业过程控制领域得到了广泛的应用，能够处理设备物理条件的约束以及各种工艺性指标的约束[2-5]，满足密炼工艺质量精益控制的要求。但对于具有时变特性的密炼过程，MPC 控制效果会随着模型预测匹配误差的增大而明显下降[6-7]。针对这一问题，本文提出机理建模与深度学习融合的模型预测方法，建立质量精益控制的模型预测控制结构。

1 密炼过程质量精益控制MPC 策略设计

密炼工艺质量精益控制MPC 结构基于预测模型的状态空间方程表达，设计滚动优化目标函数与约束，实现对产品、能源、设备要素的综合控制。

1.1 MPC 框架

本文提出MPC 方法求解步骤如下：

离线步骤：

步骤1基于键合图理论建立被控过程的机理模型；

步骤2线性化、离散化被控过程机理模型，得到线性离散状态空间方程；

步骤3建立质量精益生产优化目标函数与优化约束。

在线步骤：

步骤1辨识被控过程预测模型参数，结合机理模型得到预测模型；

步骤2测量当前时刻系统状态，计算预测时域上参考轨迹；

步骤3构建并求解二次规划问题，取未来第一时刻最优控制量作为控制器输出；

步骤4返回在线步骤2，在每一时刻滚动优化直到密炼过程结束。

1.2 基于反馈校正的模型预测

预测模型以控制增量Δu（k）作为控制变量，被控过程状态转移状态空间表达式如下：

式中：x（k）为状态变量；u（k）为输入变量；Aξ、Bξ、Cξ、Hξ为ξ 生产批次的状态空间矩阵；Δu（k）＝u（k）-u（k-1）。

预测时域上状态变量的序列表达为

式中：NC为控制时域；NP为预测时域；NC≤NP。

定义k 时刻模型预测状态与系统实际状态间的误差e（k）为

式中：x（k|k-1）=Aξx（k-1）+Bξu（k-1）+Hξ。

使用e（k）对预测模型的输出进行校正，得到：

式中：W 是误差反馈校正系数矩阵。

1.3 基于质量要素的滚动优化

密炼过程质量精益管控的要求为在对参考温度曲线准确跟踪的前提下，降低设备损耗并减少能源消耗。MPC 采用一阶曲线作为预测时域上的参考曲线，通过温度上升的平滑性来减小执行机构的变化幅度。预测时域上的参考曲线为

式中：r（k+i）＝αiy（k）+（1-αi）c（k），c（k）为k 时刻温度设定值。

MPC 控制器优化目标函数中包含温度参考轨迹跟踪误差项和控制增量抑制项：

式中：权重矩阵Q=diag｛q1，q2，…，qnx｝，R=diag｛r1，r2，…，rnu｝。抑制控制增量的频繁变动能有效降低能量消耗和设备损耗，质量、能源、设备要素间的均衡可以通过调节权重矩阵的比例实现。

将式（4）～式（6）代入优化目标函数式（7），得到关于控制增量ΔU 的标准二次规划问题：

2 机理建模与深度学习融合的预测模型

基于键合图理论建立密炼过程的传热学机理模型，得到MPC 离散线性预测模型，通过基于CNNLSTM 的系统参数辨识方法实时更新机理模型参数，保证不同工况下MPC 预测模型的高准确性。

2.1 基于键合图理论的机理建模

密炼环节中温度是重要的排胶指标[8]。密炼室内部转子转动，引起胶料与密炼室壁以及胶料之间的挤压和摩擦，令密炼室内部温度升高。流经密炼室壁的冷却水能够有效带走密炼室内热量。因此，密炼过程的控制变量为转子转速、冷却水流量，被控变量为密炼室内温度。

密炼过程传热学模型如图1 所示。系统的热源为主电机转化而来的热流量q1，密炼室内介质温度为T1；密炼室内介质通过向密炼室壁传递热量q2，密炼室壁温度为T2；密炼室壁向与其接触的冷却水部分传递热流量q3，向周围环境散失热流量q4；与密炼室壁接触冷却水温度T3，周围环境温度为T0；与密炼室壁接触冷却水与未接触冷却水之间交换的热量为q5，未接触冷却水温度即进水温度。

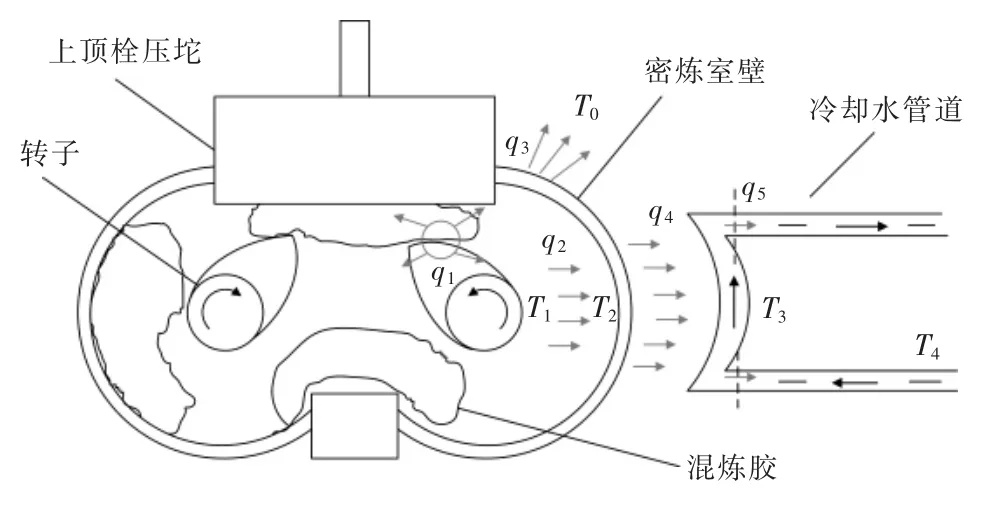
图1 密炼过程传热模型Fig.1 Heat transfer model of mixing process

键合图是一种基于功率流物理过程的图形化建模方法，将机、电、热等系统中与功率和能量相关的多物理变量统一归纳为4 种广义变量，能够表达物理过程中能量变化的情况[9]。基本元件包括阻性元件、容性元件和惯性元件，反映了系统元件普遍存在的耗散功率、储存能量的属性。系统源分为流源和势源。依据密炼过程传热模型建立的键合图模型如图2 所示。图中半箭头为功率键，每个功率键对应一个势变量e 以及流变量f。

图2 密炼过程键合图模型Fig.2 Bond graph of mixing process

密炼过程传热学模型的微分方程如下：

式中：热流源Sf 代表由电机输入的热流量；热势源Se 代表冷却水进水温度；热容C3代表密炼室内介质的等效热容，温度对应T1；C4代表密炼室壁的等效热容，温度对应T2；C5代表与密炼室壁接触冷却水的等效热容，温度对应T3；热阻反映了材料对热量传导的阻碍能力。

根据密炼机内电机生热公式[10]，将转子转速与热流源等效为线性关系：

式中：η 为传动效率；n 为转子转速；D、L 为转子形状参数；K1为等效传热系数。

密炼过程的键合图模型将冷却水分为了与密炼室壁接触的冷却水以及未与密炼室壁接触的冷却水两部分，两者之间传递的热量经过热阻R9[11]。热阻大小与冷却水流量成反比关系：

式中：Ql为冷却水流量；K2为流量-热阻系数。

将式（9）、式（10）代入式（8），得到密炼过程的状态空间表达式，对其线性化和离散化：

2.2 基于CNN-LSTM 的系统参数辨识方法

密炼过程特性随着密炼机和胶料配方的不同而变化，本文通过基于CNN-LSTM 的深度学习方法辨识被控过程的模型参数，实现预测模型与被控过程的精准匹配。本文针对固定的一组参数的密炼过程取多组不同的输入输出数据作为神经网络输入。由于时间序列维度的增加，输入数据不再适用于作为LSTM 网络的直接输入[12]，因此通过CNN 网络提取输入数据特征，降低数据维度，再通过LSTM 网络提取数据时序特征，辨识得到系统参数。本文CNNLSTM 网络结构如图3 所示。

图3 CNN-LSTM 神经网络结构Fig.3 Architecture of CNN-LSTM network

图中，Nc为CNN 输入通道数；Ns为系统输入输出量个数之和；Nt为每条时间序列采样点数；Hk为卷积核纵向维度；Nh为LSTM 隐藏层神经元数；Np为待辨识参数个数。输入数据经1 层CNN 网络提取特征得到一维时间序列输入给2 层LSTM 网络，输出数据经过维度变换后输入到全连接层，最终神经网络输出得到一维参数向量值。

2.3 参数辨识实验

限定密炼过程的系统输入量n 取值范围为［0，60］，Ql取值范围为［60，80］，系统参数取值范围如表1 所示。

表1 系统参数取值范围Tab.1 Value range of the system parameters

深度学习网络参数取值如下：Nc=50，Ns=3，Nt=320，Hk=3，Nh=256，Np=8。深度学习网络结构如表2 所示。深度学习超参数：学习率α＝0.00005，迭代次数epoch=200，批次大小batch_size=32。

表2 深度学习网络结构参数Tab.2 Structural parameters of deep learning network

在参数取值范围内取6 组待辨识参数，使用训练好的深度学习神经网络进行参数辨识。参数辨识平均误差如表3 所示。

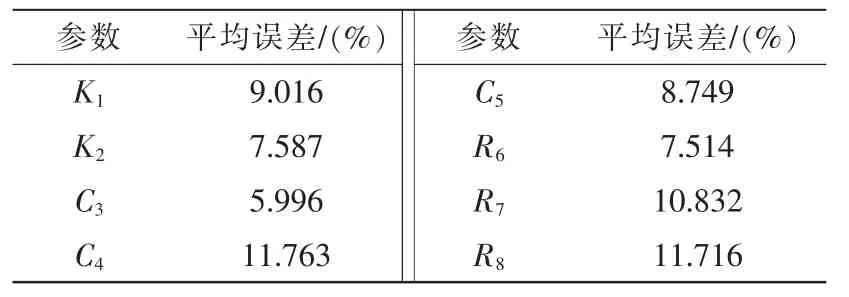
表3 参数辨识平均误差Tab.3 Result of the identification model

均方根误差能够表征实际的测量温度曲线与预测温度曲线间的误差，预测模型的均方根误差（RMSE）结果如表4 所示，两组RMSE 值对应曲线如图4 所示，实验结果说明预测模型精度较高。

表4 被控对象参数Tab.4 Parameters of controlled plants

表4 预测模型均方根误差Tab.4 Root-mean-square error of the prediction model

图4 密炼过程预测结果Fig.4 Prediction results of mixing process

3 仿真结果

3.1 多批次对比控制实验设置

为了验证本文提出模型预测方法对于时变、非线性过程的控制效果，采用3 组不同参数的被控对象，对比了PID 方法、静态模型MPC 方法以及本文提出MPC 方法的控制结果。PID 控制参数已在对象1 下将系统表现调至较优，在切换对象2、3 时保持不变。静态模型MPC 方法的预测模型保持不变，与3 组对象间都存在一定误差。本文提出的基于机理建模与深度学习的MPC 方法将对每一组对象进行系统参数辨识，建立准确的预测模型并控制。

3.2 仿真参数

控制器参数如下：预测时域Np=15，控制时域Nc=10，参考轨迹参数α＝0.7788，反馈校正系数h＝0.5，轨迹跟踪误差权重矩阵Q=diag｛0.91，0，0｝，控制增量权重矩阵R=diag｛0.91，0｝。控制增量变化范围Δn∈［-40，40］，ΔQl∈［-40，40］；状态量变化范围T1，T2，T3∈［0，200］。PID 参数KP＝4.02，KI＝0.03，KD＝0。R 的对角元素r11、r22对应控制量n 与Ql，由于电机能耗远大于冷却水流量阀的能耗，因此设r22为0，不对冷却水阀的能耗作约束。

3.3 仿真对比

控制表现衡量指标采用了稳态误差、超调量以及控制变量平均变化量。被控对象参数如表4 所示。

密炼过程实验结果如图5 所示。控制指标如表5 所示。

表5 控制指标Tab.5 Control results of mixing process

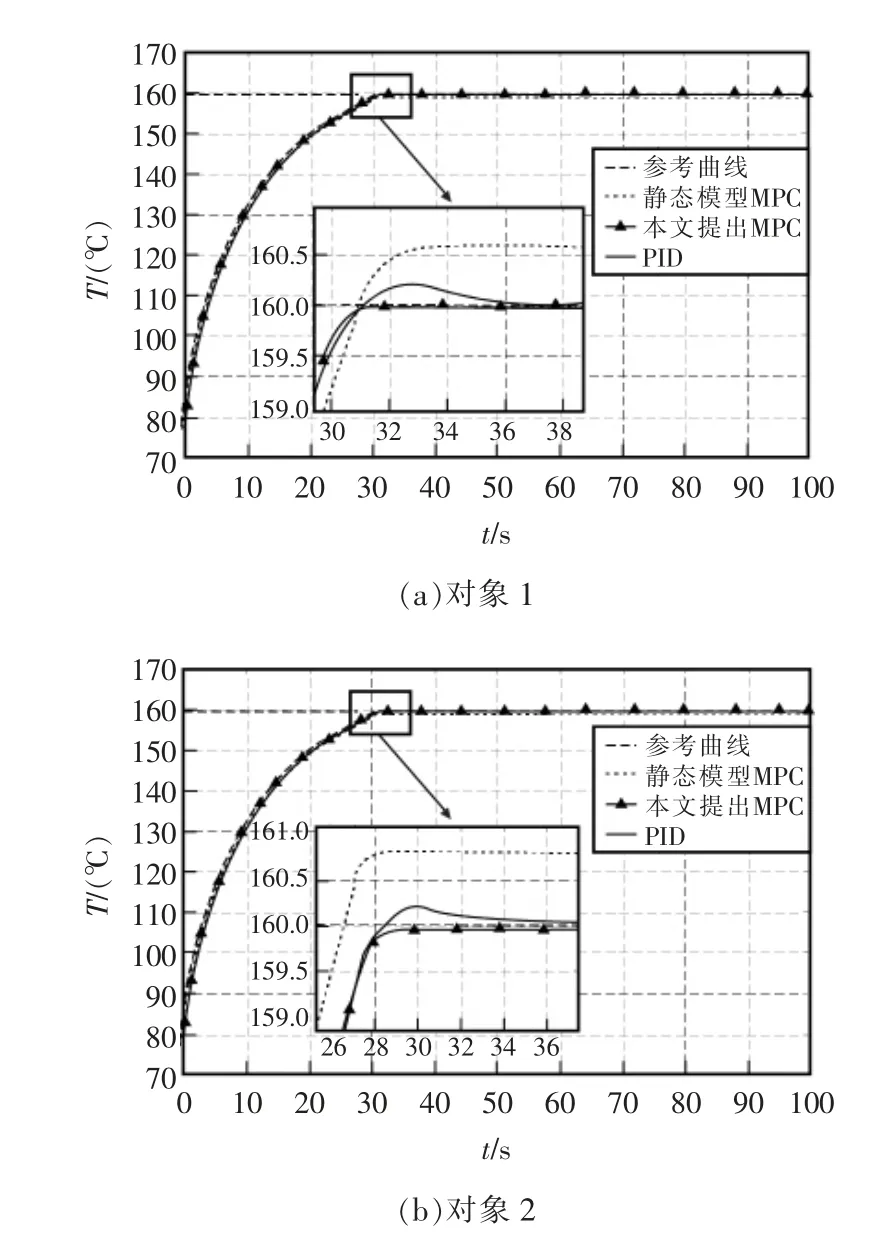
图5 密炼过程控制结果Fig.5 Control results of mixing process

3.4 结果分析

从结果可以看出，PID 在满足控制的快速性时会产生超调，而MPC 方法在选择合适的预测时域参数时则不会，这使得密炼过程的产品质量更加精益。MPC 方法能够有效抑制控制变量的变动，进而满足设备损耗和能源消耗质量要素的要求。当被控对象改变时，PID 控制的超调性能等都会变差，而静态模型MPC 方法由于模型的失配，控制效果退化严重，产生明显的稳态误差，本文提出的在线参数辨识的MPC 方法则能够保持预测模型与被控对象的匹配度，保证始终产生好的控制效果。