相似三角形与函数综合问题探究
2024-01-27王勇
王勇


[摘 要]在近几年的各地中考数学试题中,相似三角形与函数综合考查成为中考命题的热点。文章结合四个典型例题,探讨相似三角形与函数综合问题,旨在夯实学生基础,发展学生思维,培养学生核心素养。
[关键词]相似三角形;函数;综合问题
[中图分类号] G633.6 [文献标识码] A [文章编号] 1674-6058(2023)29-0010-03
在近几年的各地中考数学试题中,相似三角形与函数综合考查成为命题的热点,它包括相似三角形与一次函数综合、相似三角形与反比例函数综合、相似三角形与二次函数综合、相似三角形与绝对值函数综合。下面笔者结合例题逐一分析探讨。
一、相似三角形与一次函数综合
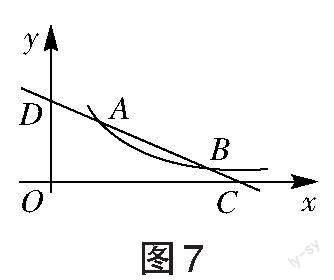
一次函数的图象是一条直线,它与两坐标轴相交形成直角三角形,以原点为直角顶点再放置一个相似的直角三角形,会形成“手拉手”相似三角形模型,利用相似三角形的性質可以求线段的长度,确定线段的最小值等。
解析:(1)利用两角对应相等的两个三角形相似,得[△BDC ]∽[△EDO],从而得证。∵[OC⊥OE],∴[∠COE=90°],∴[∠AOB=∠COE=90°],∵[∠OCD=∠OAB],∴[∠ABO=∠CEO],∵[∠BDC=∠EDO],
(3)根据[OA=OF]可知,F在以O为圆心,以OA为半径的半圆上运动,在[△OBF]中,由三角形的三边关系,得[BF>OF-OB],所以当F在y轴上,且在B的上方时,BF的值最小,由此得到BF的最小值。如图5所示,由对称得:[OA=OF],动点F在以O为圆心、以OA为半径的半圆[AFA']上运动,因为[OB=6],在[△OBF]中,由三角形的三边关系得[BF>OF-OB],所以当F在y轴上,且在B的上方时,BF的值最小,如图6所示,此时[BF=OF-OB=8-6=2],即BF的最小值是2。
二、相似三角形与反比例函数综合
相似三角形与反比例函数综合问题主要考查相似三角形存在性问题、三角形面积等,要求学生掌握相似三角形的判定、反比例函数的性质等,且要具备分类讨论、数形结合等数学思想方法。
三、相似三角形与二次函数综合
[例3]如图9所示,在平面直角坐标系中,二次函数[y=mx2+nx+4]([m≠0])的图象交[x]轴于A、B两点,交y轴于点C,点A的坐标为[(-3,0)],点B的坐标为(1,0),以OA、OC为边作矩形OADC,且边CD交二次函数的图象于点M。(1)求二次函数的表达式;(2)现有一条垂直于x轴的直线[x=a]在[A]、[O]两点间(不包括A、O两点)左右移动,分别交x轴于点E,交CD于点F,交AC于点P,交二次函数的图象于点Q,请用含a的代数式表示QP的长;(3)在(2)的条件下,连接QC,则在CD上方的二次函数的图象上是否存在这样的点Q,使得以Q、C、F为顶点的三角形和[△AEP]相似?若存在,直接写出a的值;若不存在,请说明理由。
四、相似三角形与绝对值函数综合
绝对值函数的本质还是分段函数,它的函数图象一般为轴对称图形,在绝对值函数里也会讨论相似三角形的存在性问题。
