2023年高考之导数考点解读

■许昌市高中数学胡银伟名师工作室 胡银伟

导数是研究函数的有力工具,导数与函数、不等式、向量、解析几何、数列等知识的交汇是高考命题的热点和难点,主要考查导数的工具性,同学们的综合解题能力、数学的应用意识及数学素养。

从高考命题形式及内容来看:选填题主要考查导数概念、运算、性质与几何意义等;解答题主要是以函数为载体,利用导数研究函数的单调性、极值、最值,利用导数证明不等式或探讨方程的根,利用导数求解参数的值或取值范围等。从高考命题难度来看:导数高考试题一般采取分层设问和螺旋式上升的方式,即先以较易的问题考查同学们对基础知识的掌握情况,再逐步增加难度,以逐步提高同学们的解题能力和思维水平。总体而言,导数高考命题具有较高的难度和综合性,需要大家具备扎实的基础知识和较强的解题能力。

下面我们结合2023年高考真题,对导数高考考点进行解读。

考点一 对导数的几何意义的考查

例1【2023年全国甲卷文科第8题】曲线在点处的切线方程为( )。

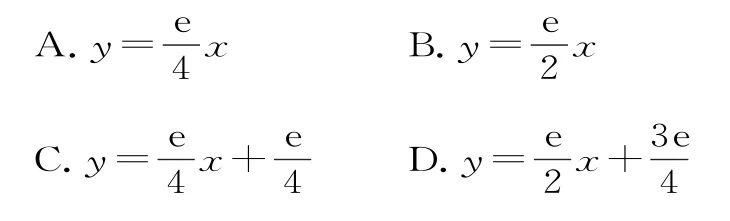
命题意图:本题考查导数计算及导数的几何意义等知识,考查数学运算的核心素养。

解题思路:先求函数的导函数,代入切点的横坐标可得切点处的导数值,即切点处的切线斜率,由直线方程的点斜式可得所求切线的方程。

考点解读:应用导数的几何意义解题时应注意:1.求曲线的切线方程时要注意“过点P的切线”与“在点P处的切线”的差异,过点P的切线,点P不一定是切点,点P也不一定在已知曲线上,而在点P处的切线,必以点P为切点;2.函数在某点处的导数值就是对应曲线在该点处切线的斜率,切点既在原函数的图像上也在切线上。

考点二 利用导数研究函数的单调性

例2【2023 年全国乙卷理科第16题】设a∈(0,1),若函数f(x)=ax+(1+a)x在(0,+∞)上单调递增,则a的取值范围是_____。

命题意图:本题是考查利用导数研究函数的单调性,考查逻辑推理及数学运算的核心素养。

解题思路:原问题等价于f'(x)=axlna+(1+a)xln(1+a)≥0 恒成立,据此将所得不等式进行恒等变形,可得由函数的单调性构建实数a的不等式,解不等式得实数a的取值范围。

解析:由函数的解析式可得f'(x)=axlna+(1+a)xln(1+a)≥0 在 区 间(0,+∞)上恒成立,则(1+a)xln(1+a)≥-axlna,即在区间(0,+∞)上恒成立。

考点解读:已知函数的单调性,求参数的取值范围,利用条件f'(x)≥0(或f'(x)≤0),x∈(a,b)恒成立,解出参数的取值范围(一般可用不等式恒成立的理论求解),应注意参数的取值是f'(x)不恒等于0的参数的范围。

例3【2023 年全国乙卷文科第20题】已知函数

(1)当a=-1时,求曲线y=f(x)在点(1,f(1))处的切线方程;

(2)若函数f(x)在(0,+∞)上单调递增,求实数a的取值范围。

命题意图:本题考查导数的几何意义、利用导数研究函数的单调性等知识,还考查逻辑推理及数学运算的核心素养。

解题思路:(1)由题意首先确定导函数的解析式,由导数的几何意义确定切线的斜率和切点坐标,再求切线的方程;(2)原问题即f'(x)≥0在区间(0,+∞)上恒成立,整理变形可得g(x)=ax2+x-(x+1)ln(x+1)≥0在区间(0,+∞)上恒成立,分a≤0三种情况进行讨论,可得实数a的取值范围。

解析:(1)当a= -1 时,f(x)=

函数在(1,f(1))处的切线方程为y-0=-(x-1)ln 2,即xln 2+y-ln 2=0。

(2)由函数的解析式可得f'(x)=-1),满足题意时f'(x)≥0在区间(0,+∞)上恒成立。

令g(x)=ax2+x-(x+1)ln(x+1),原问题等价于g(x)≥0 在区间(0,+∞)上恒成立,则g'(x)=2ax-ln(x+1)。

①当a≤0时,由于2ax≤0,ln(x+1)＞0,故g'(x)＜0,g(x)在区间(0,+∞)上单调递减,此时g(x)＜g(0)=0,不符合题意。

令h(x)=g'(x)=2ax-ln(x+1),则

考点解读:1.由函数的单调性求参数的取值范围常见题型如下。(1)若可导函数f(x)在区间M上单调递增,则f'(x)≥0(x∈M)恒成立;若可导函数f(x)在区间M上单调递减,则f'(x)≤0(x∈M)恒成立;(2)若可导函数在某区间上存在单调递增(减)区间,则f'(x)＞0(或f'(x)＜0)在该区间上存在解集;(3)已知f(x)在区间I上的单调性,当区间I中含有参数时,可先求出f(x)的单调区间,I是其单调区间的子集。

2.利用导数研究函数单调性的关键:(1)在利用导数讨论函数的单调区间时,要确定函数的定义域;(2)单调区间的划分要注意对导数等于零的点的确认;(3)已知函数单调性求参数范围,要注意导数等于零的情况。

考点三 利用导数研究函数的极值、最值

例4(1)【2023年新课标全国Ⅱ卷第11题】(多选)若函数(a≠0)既有极大值也有极小值,则( )。

A.bc＞0 B.ab＞0

C.b2+8ac＞0 D.ac＜0

(2)【2023年新课标全国Ⅱ卷第6题】已知函数f(x)=aex-lnx在区间(1,2)上单调递增,则a的最小值为( )。

A.e2B.e C.e-1D.e-2

命题意图:本题是考查利用导数研究函数的极值、最值等知识,考查逻辑推理及数学运算的核心素养。

解题思路:(1)求出函数f(x)的导数f'(x),由已知可得f'(x)在(0,+∞)上有两个变号零点,从而将问题转化为一元二次方程有两个不等的正根进行解答。(2)根据f'(x)在(1,2)上恒成立,分离参数求最值即可。

故b2+8ac＞0,ab＞0,ac＜0。显然a2bc＜0,即bc＜0,A 错误,BCD 正确。选BCD。

考点解读:1.利用导数研究函数极值、最值的方法:(1)若求极值,则先求方程f'(x)=0的根,再检查f'(x)在方程根的左右时函数值的符号;(2)若已知极值大小或存在情况,则转化为已知方程f'(x)=0根的大小或存在情况来求解;(3)求函数f(x)在闭区间[a,b]上的最值时,在求得极值的基础上,结合区间端点的函数值f(a),f(b)与f(x)的各个极值比较得到函数的最值。

2.利用导数研究函数的极值、最值应注意的问题:(1)不能忽略函数f(x)的定义域;(2)f'(x0)=0是可导函数f(x)在x=x0处取得极值的必要不充分条件;(3)函数的极小值不一定比极大值小;(4)函数在区间(a,b)上有唯一极值点,则这个极值点也是最大(小)值点,此结论在导数的实际应用中经常用到。

考点四 利用导数研究函数的零点问题

例5【2023年全国乙卷文科第8题】函数f(x)=x3+ax+2存在3个零点,则a的取值范围是( )。

A.(-∞,-2) B.(-∞,-3)

C.(-4,-1) D.(-3,0)

命题意图:本题是考查利用导数研究函数的零点的知识内容,考查逻辑推理及数学运算的核心素养。

解题思路:求得f'(x)=3x2+a,并求出极值点,转化为极大值大于0且极小值小于0即可。

解析:因为f(x)=x3+ax+2,所以f'(x)=3x2+a。若f(x)存在3个零点,则f(x)要存在极大值和极小值,即a＜0。

考点解读:1.判断、证明函数零点个数的方法:(1)令f(x)=0,则方程解的个数即为零点的个数;(2)利用单调性与零点存在性定理求解;(3)化原函数为两个函数,利用两个函数图像交点的个数来求解。2.根据函数零点情况求参数范围的常用方法:(1)分离参数(a=g(x))后,将原问题转化为y=g(x)的值域(最值)问题或转化为直线y=a与y=g(x)图像的交点个数问题(优选分离、次选分类)求解;(2)利用零点存在性定理构建不等式进行求解;(3)转化为两个熟悉的函数图像的位置关系问题,从而构建不等式求解。

考点五 导数与不等式

角度1 利用导数研究不等式的恒成立、存在性问题

例6【2023年全国甲卷理数第20题】已知函数

(1)当a=8时,讨论f(x)的单调性;

(2)若f(x)＜sin 2x恒成立,求a的取值范围。

命题意图:本题是利用导数研究函数的单调性及不等式的恒成立问题,考查逻辑推理、数学运算及数学建模的核心素养。

解题思路:(1)求导,然后令t=cos2x,讨论导数的符号得所求;(2)构造函数g(x)=f(x)-sin 2x,计算g'(x)的最大值,然后与0比较大小,得出a的分界点,再对a进行讨论即可。

所以当a∈(-∞,3]时,f(x)＜sin 2x,符合题意。

②若a∈(3,+∞),当t→0,

所以φ(t)→-∞,φ(1)=a-3＞0。

因此,∃t0∈(0,1),使得φ(t0)=0,即,使得g'(x0)=0。当t∈(t0,1)时,φ(t)＞0,即当x∈(0,x0)时,g'(x)＞0,g(x)单调递增。

所以当x∈(0,x0)时,g(x)＞g(0)=0,不符合题意。

综上,a的取值范围为(-∞,3]。

考点解读:1.由不等式恒成立求参数的取值范围问题的策略:(1)求最值法,将恒成立问题转化为利用导数求函数的最值问题;(2)分离参数法,将参数分离出来,进而转化为a＞f(x)max或a＜f(x)min的形式,通过导数的应用求出f(x)的最值,即得参数的取值范围。2.对于含参数的不等式,如果易分离参数,那么可先分离参数,然后构造函数,将问题直接转化为求函数的最值问题,否则应进行分类讨论。在解题过程中,必要时可作出函数图像,借助几何图形直观分析。

角度2 利用导数研究不等式中的参数问题

例7【2023年全国甲卷文科第20题】已知函数

(1)当a=1时,讨论f(x)的单调性;

(2)若f(x)+sinx＜0,求a的取值范围。

命题意图:本题考查利用导数研究函数的单调性、求不等式的含参问题,还考查逻辑推理、数学运算及数学建模的核心素养。

解题思路:(1)代入a=1,对f(x)求导,同时利用三角函数的平方关系化简f'(x),再利用换元法判断其分子与分母的正负情况,从而得解。(2)方法一,构造函数g(x)=f(x)+sinx,从而得到g(x)＜0,注意到g(0)=0,从而得到g'(0)≤0,进而得到a≤0,分类讨论a=0 与a＜0 两种情况即可得解;方法二,先化简并判断得0恒成立,再分类讨论a=0,a＜0与a＞0三种情况,利用零点存在性定理与隐零点的知识判断当a＞0时不满足题意,从而得解。

解析:(1)因为a=1,所以f(x)=x-

注意到g(0)=0,所以g(x)＞g(0)=0,即f(x)+sinx＞0,不满足题意。

此时g'(x)在(0,x1)上有g'(x)＞0,所以g(x)在(0,x1)上单调递增。

则在(0,x1)上有g(x)＞g(0)=0,即f(x)+sinx＞0,不满足题意。

综上可得,a≤0。

考点解读:1.利用导数研究含参数的不等式问题,若能够分离参数,则常先将问题转化为形如a≥f(x)(或a≤f(x))的形式,再通过求函数f(x)的最值求得参数范围。一般地,若a＞f(x)对x∈D恒成立,则只需a＞f(x)max;若a＜f(x)对x∈D恒成立,则只需a＜f(x)min。若存在x∈D,使a＞f(x)成立,则只需a＞f(x)min;若存在x∈D,使a＜f(x)成立,则只需a＜f(x)max。由此构造不等式,求解参数的取值范围。2.解不等式求参问题时,常会通过不等式的同解变形,构造一个与背景函数相关的函数,利用函数最值确定参数的取值范围。在构造函数或求最值过程中常用到放缩法,如函数放缩法,基本不等式放缩法,叠加不等式放缩法等。

角度3 利用导数证明不等式

例8【2023年新课标全国Ⅰ卷第19题】已知函数f(x)=a(ex+a)-x。

(1)讨论f(x)的单调性;

(2)证明:当a＞0时

命题意图:本题考查利用导数研究函数的单调性及证明不等式等知识,还考查逻辑推理、数学运算及数学建模的核心素养。

解题思路:(1)先求导,对a≤0 与a＞0两种情况分类讨论,结合导数与函数单调性的关系可得解。(2)方法一,结合(1)中结论,将问题转化为的恒成立问题,构造函数利用导数证得g(a)＞0 即可;方法二,构造函数h(x)=ex-x-1,证得ex≥x+1,从而得到f(x)≥x+lna+1+a2-x,进而将问题转化为的恒成立问题,由此得证。

解析:(1)已知f(x)=a(ex+a)-x,定义域为R,则f'(x)=aex-1。

当a≤0 时,由于ex＞0,则aex≤0,故f'(x)=aex-1＜0 恒成立,f(x)在R 上单调递减。

当a＞0时,令f'(x)=aex-1=0,解得x=-lna。

当x＜-lna时,f'(x)＜0,则f(x)在(-∞,-lna)上单调递减;

当x＞-lna时,f'(x)＞0,则f(x)在(-lna,+∞)上单调递增。

综上,当a≤0 时,f(x)在R 上单调递减;当a＞0时,f(x)在(-∞,-lna)上单调递减,在(-lna,+∞)上单调递增。

(2)(方法一)由(1)得,f(x)min=f(-lna)=a(e-lna+a)+lna=1+a2+lna。

所以当a＞0时,恒成立,证毕。

(方法二)令h(x)=ex-x-1,则h'(x)=ex-1。

因为y=ex在R 上单调递增,所以h'(x)=ex-1在R 上单调递增。

又h'(0)=e0-1=0,所以当x＜0 时,h'(x)＜0;当x＞0时,h'(x)＞0。

所以h(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增,故h(x)≥h(0)=0,即ex≥x+1,当且仅当x=0时,等号成立。

考点解读:利用导数证明不等式的基本方法如下。(1)利用单调性:若f(x)在[a,b]上是增函数,则①∀x∈[a,b],有f(a)≤f(x)≤f(b);②∀x1,x2∈[a,b],且x1＜x2,有f(x1)＜f(x2)。对于减函数有类似结论。(2)利用最值:若f(x)在某个范围D内