稳定连续半格的闭包空间表示

王胜文, 张 冰, 马俊叶, 王龙春

(①六盘水师范学院数学与统计学院,553004,贵州省六盘水市;②曲阜师范大学数学科学学院,273165,山东省曲阜市;③太原科技大学应用科学学院,030024,山西省太原市)

0 引 言

基于序、拓扑、范畴论等的Domain理论为计算机程序语言的指称语义构建了具有可计算性的数学模型. 寻求各种domain结构具体而易于理解的表示形式一直是Domain理论研究中的一个热点问题. 国内外许多学者利用信息系统[1,2]、形式概念分析[3,4]、逻辑演算[5,6]等不同数学工具在此领域已做了许多卓有成效的研究.

闭包空间作为一种重要的数学工具也已被广泛地用以刻画各种序与代数结构,关于闭包空间的表示综述性文章可参阅文献[7]. 在Domain理论中,一个众所周知的结论是代数格带有Scott连续映射构成的范畴可由代数闭包空间所表示,这一重要的发现激励了众多学者进一步探讨闭包空间与各种domain结构的内在联系,尤其是国内的一些学者在这方面更是做了很多有意义的工作. 2015年,郭兰坤等人提出了一种F-可乘闭包空间的概念,实现了代数domain范畴的闭包空间表示[8];2019年张清霞在其硕士毕业论文中为算术半格找到了合适的闭包空间描述[9];2021年吴明渊等人建立了一种新的代数domain的闭包空间表示形式,并在此基础上得到了代数L-domain的闭包空间刻画[10];同年,姚灵娟等人建立了双有限domain范畴的闭包空间表示[11]. 上述提及的各种domain结构的闭包空间表示都局限于代数domain或者它的某个满子范畴上. 2018年,文献[12]首次为连续domain范畴找到了一种合适的闭包空间表示,并由此给出了连续L-domain,有界完备domain等子范畴的表示方法. 若将这一方法限制在代数情形,也可用以刻画代数domain,代数L-domain以及Scott-domain等范畴. 2021年李庆国等人利用文献[12]提出的思想给出了连续格的一种闭包空间表示[13].

我们知道算术半格是稳定连续半格的代数形式,虽然算术半格已找到了合适的闭包空间表示,但据我们所知稳定连续半格的闭包空间表示仍是未知的. 本文将在文献[12]的基础上给出稳定连续半格的闭包空间表示. 文章内容安排如下:预备知识回顾了本文将要用到的Domain理论的知识,同时也回顾了文献[12]的一些重要结论;文章的主要结果部分首先给出了可乘闭包空间的概念,其次利用可乘闭包空间中正则闭集的概念得到了稳定连续半格的表示定理,然后引入稳定连续半格间逼近映射的概念,并在此基础上构建了与稳定连续半格等价的可乘闭包空间范畴.

1 预备知识

本节第1部分回顾了本文所需要的关于序与Domain理论的基础知识,第2部分概括了连续domain的闭包空间表示的一些相关结果.

1.1 序与Domain

本小节中相关的概念和性质可参阅Domain理论的经典文献[14,15].

设X为偏序集(P,≤)的子集.用∨X和∧X分别表示X的上确界和下确界.特别地,记x∧y=∧{x,y},其中∧称为交算子.若偏序集P中任意两个元的交都存在,则称偏序集为一个交半格,简称半格.设D为偏序集P的一个非空子集,如果D的每个非空有限子集都有上界,则称D为定向集.若偏序集P的每个定向子集的上确界都存在,则称P是定向完备集,简称为dcpo.

用F⊆fA表示F是集合A的一个有限子集, 并用F≪y表示F中的每个元x∈F都满足x≪y. 连续domainP满足如下的插入性:设BP为P的一个基,y∈P且M⊆fP,若M≪y,则存在z∈BP使得M≪z≪y成立.

定义1.1若连续domainD也是一个半格,则称其为连续半格. 连续半格D中的逼近关系≪若满足:当a≪b,c时有a≪b∧c,则称D是稳定连续半格,这时称逼近关系≪是可乘的.

定义1.2 设P和Q为连续domain. 若映射f:P→Q满足对P的任意定向子集D而言都有

则称映射f:P→Q是Scott连续的.

事实上,从连续domainP到Q的Scott连续映射就是关于P和Q上的Scott拓扑而言的连续映射. 所有的稳定连续半格带有其上的Scott连续映射构成了一个范畴,记作SD.

1.2 连续domain的闭包空间表示

一般地,闭包空间有两种相互等价的定义形式:一种是一个集合带有它的某个子集族构成的有序对;另一种是一个集合带有其集族上的一个算子. 本文采用了第二种形式.

定义1.3[7］设X为集合,P(X)为X的幂集族. 若映射γ:P(X)→P(X)对任意的A、B⊆X,满足

(1)A⊆γ(A);

(2)γ(γ(A))=γ(A);

(3) 当A⊆B时,γ(A)⊆γ(B).

则称映射γ为闭包算子,并称二元组(X,γ)为一个闭包空间.

定义1.4[12］设(X,γ)为闭包空间. 若映射τ:⊆P(X)→P(X)对任意的A、B⊆X,满足以下条件

(1)τ(γ(A))⊆γ(A);

(2)τ(τ(γ(A)))=τ(γ(A));

(3) 当A⊆B时,τ(γ(A))⊆τ(γ(B)).

则称二元组(X,τ∘γ)为一个广义闭包空间. 为方便起见,常记τ∘γ(A)为〈A〉.

定义1.5[12］设(X,τ∘γ)为广义闭包空间,P为X的一些有限子集构成的非空子集族. 若对任意的F∈F和M⊆f〈F〉都存在F1∈F使得M⊆〈F1〉且F1⊆〈F〉,则称(X,τ∘γ,F)为一个连续闭包空间.

定义1.6[12］设(X,τ∘γ,F)为一个连续闭包空间,U为X的一个非空子集. 若对任意的M⊆fU都存在F∈F使得M⊆〈F〉⊆U,则称U为(X,τ∘γ,F)的正则闭集.

连续闭包空间(X,τ∘γ,F)的所有正则闭集之族记作R(X).

引理1.1[12］设(X,τ∘γ,F)为一个连续闭包空间.

(1)若F∈F,则〈F〉是一个正则闭集.

(2)U为一个正则闭集当且仅当集族{〈F〉|F∈F,F⊆U}是定向的且U=∪{〈F〉|F∈F,F⊆U}.

(4)若U1、U2为定向正则集,则

U1≪U2⟺(∃F∈F)(U1⊆〈F〉,F⊆U2).

(1)

(5)若U为正则闭集且M⊆fU,则存在F∈F使得F⊆U且M⊆〈F〉⊆U.

引理1.2[12］设(X,τ∘γ,F)为一个连续闭包空间. 则R(X)在集合包含关系下构成一个连续domain.

令F为BD的所有具有最大元的有限子集之族. 则对任意的F∈F,有∨F∈F且

(2)

这时有如下结论.

引理1.3[12］设BD为连续domain(D,≤)的一个基,则上述定义的三元组(BD,τ∘γ,F)为一个连续闭包空间.

2 主要结果

2.1 表示定理

本节将给出稳定连续半格基于闭包空间的表示形式,为此需引入如下定义.

定义2.1 设(X,τ∘γ,F)为连续闭包空间. 若对任意的F1、F2、G1、G2∈F,有

(M1)M⊆f〈F1〉∩〈F2〉⟹(∃F∈F)(F⊆〈F1〉∩〈F2〉,M⊆〈F〉),

(M2)G1⊆〈F1〉,G2⊆〈F2〉⟹(∃F,G∈F)(〈G1〉∩〈G2〉⊆〈G〉,G⊆〈F〉⊆〈F1〉∩〈F2〉).

则称(X,τ∘γ,F)为可乘闭包空间.

定理2.1 设(X,τ∘γ,F)为一个可乘闭包空间. 则R(X)在集合包含关系下构成一个稳定连续半格.

证明根据引理1.2知R(X)在集合包含关系下是一个连续domain. 为证明(R(X),⊆)为稳定连续半格,只需验证(R(X),⊆)是一个半格且其上的逼近关系是可乘的.

设U1、U2∈R(X). 当M⊆fU1∩U2时,由定义1.6知存在F1、F2∈F使得M⊆f〈F1〉⊆U1以及M⊆f〈F2〉⊆U2. 因此M⊆f〈F1〉∩〈F2〉⊆U1∩U2. 又(X,τ∘γ,F)为一个可乘闭包空间,根据条件(M1)可知存在F∈F使得F⊆f〈F1〉∩〈F2〉⊆U1∩U2且M⊆f〈F〉. 这说明U1∩U2∈R(X). 故(R(X),⊆)为半格,其中半格算子恰为集合之间的交运算.

下证(R(X),⊆)上的逼近关系是可乘的. 设U1、U2、U3∈R(X)且U3≪U1,U3≪U2. 由等式(1)知存在Gi∈F使得U3⊆〈Gi〉以及Gi⊆Ui成立,其中i=1,2. 因为Gi是正则闭集Ui的一个有限子集,因此由定义6知存在Fi∈F使得Gi⊆〈Fi〉⊆Ui,i=1,2. 又因为(X,τ∘γ,F)为可乘闭包空间,由条件(M2) 可得F、G∈F满足〈G1〉∩〈G2〉⊆〈G〉且G⊆〈F〉⊆〈F1〉∩〈F2〉. 故U3≪U1∩U2.

定理2.2设BL为稳定连续半格(L,≤)的一个基,则引理3中引入的(BL,τ∘γ,F)为可乘闭包空间.

证明引理1.3已证明(BL,τ∘γ,F)为连续闭包空间,下面只需验证对任意的F1、F2、G1、G2∈F而言条件(M1)和(M2)成立.

下证条件(M2). 如果G1⊆〈F1〉,G2⊆〈F2〉,则∨G1≪∨F1且∨G2≪∨F2. 从而存在d1、d2∈BL使得∨G1∧∨G2≪d1≪d2≪∨F1∧∨F2.

令F={d2},G={d1}. 则〈G1〉∩〈G2〉⊆〈G〉且G⊆〈F〉⊆〈F1〉∩〈F2〉.

定理2.3(表示定理) 设BL为稳定连续半格(L,≤)的基. 则存在从(L,≤)到稳定连续半格(R(BL),⊆)的序同构映射f:L→R(BL),且f:L→R(BL)及其逆映射都是Scott连续的.

由f和g的上述定义方式不难发现它们是保序且互逆的. 因此稳定连续半格(L,≤)和(R(BL),⊆)是序同构的. 又由f和g的互逆性,对于结论的第2部分,只需验证映射f的Scott连续性即可.

故∪f(∨E)⊆∪f(E). 结论得证.

2.2 范畴等价

从范畴的角度上讲,上一小节利用可乘闭包空间实现了稳定连续半格范畴对象上的刻画. 本小节将引入可乘闭包空间之间的态射,并由此将稳定连续半格的表示定理发展为范畴等价.

(A1)FΘF′⟹FΘ〈F′〉,其中FΘF′是指对任意的x′∈F′都有FΘx′;

(A2)(F⊆f〈F1〉,FΘM′)⟹F1ΘM′;

(A3)FΘM′⟹(∃G∈F,G′∈F′)(G⊆f,M′⊆G′,GΘG′).

则称二元关系Θ⊆F×X′为从(X,τ∘γ,F)到(X′,τ′∘γ′,F′)的一个逼近映射,并记作Θ:X→X′.

性质2.1 可乘闭包空间族带有其上的逼近映射构成了一个范畴,记作ZB.

证明设Θ是从(X,τ∘γ,F)到(X′,τ′∘γ′,F′)的逼近映射,Θ′是从(X′,τ′∘γ′,F′)到(X″,τ″∘γ″,F″)的逼近映射. 定义二元关系Θ∘Θ′⊆F×X″:

F(Θ∘Θ′)x″⟺(∃G∈F′)(FΘG,GΘ′x″).

(3)

再定义二元关系

idX={(F,x)∈F×X|x∈〈F〉}.

(4)

不难验证Θ∘Θ′是一个从(X,τ∘γ,F)到(X″,τ″∘γ″,F″)的逼近映射且idX为(X,τ∘γ,F)自身上的逼近映射. 类似一般关系结合律的证明方式,不难验证由表达式(3) 定义的复合运算∘是结合的,而定义2.2的前两个条件保证了关系idX恰为(X,τ∘γ,F)上的单位态射.

对(X,τ∘γ,F)任意的正则闭集U,记

Θ(U)={x′∈X′|(∃F∈F)(F⊆fU,FΘx′)}.

(5)

引理2.1 设Θ为从(X,τ∘γ,F)到(X′,τ′∘γ′,F′)的逼近映射. 若U为(X,τ∘γ,F)的正则闭集,则Θ(U)为(X′,τ′∘γ′,F′)的正则闭集.

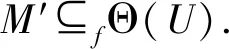
引理2.2 设BL和BL′分别为稳定连续半格(L,≤)和(L′,≤′)的基,Θ是一个从可乘闭包空间(BL,τ∘γ,F)到(BL′,τ′∘γ′,F′)的逼近映射,则如下定义的映射fΘ:L→L′,

(6)

是Scott连续的.

(7)

下面通过验证L的任意定向子集S都满足fΘ(∨S)=∨fΘ(S)来证明fΘ是Scott连续的.

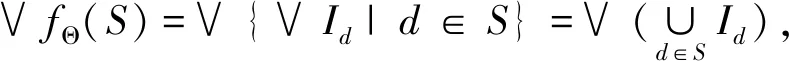
引理2.3G:ZB→SD是一个函子,其把每个可乘闭包空间(X,τ∘γ,F)映射为稳定连续半格(R(X),⊆),并把每个逼近映射Θ:X→X′映射为引理2.2中定义的Scott连续映射fΘ:R(X)→R(X′).

证明根据定理2.1以及引理2.2知G的定义是有意义的.

对任意的U∈R(X),有

G(idX)(U)=ΘidX(U)={x∈X|(∃F∈F)(F⊆fU,x∈〈F〉})

=∪{〈F〉|(∃F∈F)(F⊆fU)}=U.

上式表明G保单位态射. 设Θ:X→X′,Θ′:X′→X″为两个逼近映射. 对任意的U∈R(X)和x″∈X″,有

x″∈G(Θ′∘Θ)(U)⟺x″∈fΘ′∘Θ(U)⟺(∃F∈F)(F⊆fU,G(Θ′∘Θ)x″)⟺

(∃F∈F,∃G∈F′)(F⊆fU,FΘG,GΘ′x″)⟺(∃G∈F′)(G∈fΘ(U),GΘ′x″)⟺

(∃G∈F′)(G⊆fG(Θ)(U),GΘ′x″)⟺x″∈fΘ′(G(Θ)(U))⟺x″∈G(Θ′)(G(Θ)(U)),

这说明G(Θ′∘Θ)=G(Θ′)∘G(Θ),因此G保复合.

有了以上的准备工作,下面来证明本文的主要结论.

定理2.4 范畴ZB与SD等价.

证明定理2.3已刻画了两个范畴对象间的对应关系,下面还需证明引理2.3中定义的函子G:ZB→SD是忠实且完全的.

设Θ1,Θ2:X→X′都是从可乘闭包空间(X,τ∘γ,F)到可乘闭包空间(X′,τ′∘γ′,F′)的逼近映射且fΘ1=fΘ2,其中fΘ1和fΘ2是由引理2.2所定义的Scott连续映射. 对任意的F∈F以及x′∈X′,有

FΘ1x′⟺∃G∈F(G⊆fF,GΘ1x′)⟺x′∈fΘ1(〈F〉)⟺x′∈fΘ2(〈F〉)

⟺∃G∈F(G⊆fF,GΘ2x′)⟺FΘ2x′,

因此Θ1=Θ2. 这说明函子G是忠实的.

设BL为稳定连续半格(L,≤)的基,BL′为稳定连续半格(L′,≤′)的基. 对任意的Scott连续映射f:L→L′,定义二元关系Θf⊆F×L′:FΘfx′⟺x′≪′f(∨F).不难证明Θf是一个从(BL,τ∘γ,F)到(BL′,τ′∘γ′,F′)的逼近映射. 仅以条件(A3)为例来验证,因为(A1)和(A2)是类似的.

对任意的x∈L,因为

=∨{x′∈BL′|(∃y∈BL)(y≪x,x′≪′f(y))}

所以f=fΘf. 又因为G(Θf)=fΘf,所以G(Θf)=f,故函子G是完全的.