砂土场地桩-筒复合基础地震响应离心振动台试验

2024-01-26张泽旺梁发云王奕康田会元

哈尔滨工业大学学报 2024年2期

杨威,张泽旺,梁发云,王奕康,田会元

(1.中国长江三峡集团有限公司,武汉 430010;2.岩土及地下工程教育部重点实验室(同济大学),上海 200092;3.上海勘测设计研究院有限公司,上海 200434)

中国近海的部分海上风电场位于饱和的软弱砂层,地震可能会造成土体强度降低,导致风机结构水平位移、加速度响应等不利影响。关于近海砂土场地受荷的动力响应规律,许多学者进行了相关研究。对于单桩的地震响应规律,Haeri等[1]和张鑫磊等[2]通过1g振动台试验考虑了砂土场地的倾角、砂土层埋深等因素对单桩基础动力特性的影响,Boulanger等[3]通过一系列离心振动台试验,评估了p-y方法对桩土相互作用的分析能力。对于群桩基础地震响应规律,Abdoun等[4-5]开展了离心机振动台试验,分析了桩土相互作用以及基础的弯矩分布规律;Brandenberg等[6]进行了不同桩径的单桩与群桩场地离心试验,探究了地震荷载作用下桩周土的侧向位移;梁发云等[7]开展了单桩和群桩的动力离心试验,分析了土层厚度、输入波振幅等对体系的影响。为探究环境荷载与地震荷载耦合作用下的基础响应规律,Zheng等[8]通过缩尺振动台试验,测试了波浪、地震耦合荷载下单桩风机的动力响应;朱斌等[9]和Zheng等[8]分别考虑了单桩基础海上风机承受风浪荷载以及风浪、地震耦合作用的情况开展离心试验,比较了不同工况下的结构响应。

为保障风机在复杂海域环境和地质条件下安全平稳运行,一种新型的单桩-筒型复合基础(简称桩-筒复合基础)被提出,该基础结合了单桩基础与吸力筒基础的优点,可同时发挥两种基础形式的承载优势。对于吸力筒基础以及新型复合基础的地震响应研究,丁红岩等[10-11]研究了桩-筒组合基础的水平承载性能,考虑了基础的几何尺寸以及土层特性对组合基础承载特性的影响。Li等[12]和Wang等[13]针对桩-筒复合基础与桩盘复合基础等新型海上风电基础开展了离心振动台试验,研究了其在饱和砂土层中的地震响应规律。陈广思[14]对筒型基础等宽浅式基础结构的风机开展了数值模拟和模型试验研究,结果发现,在倾覆荷载作用时,基础较显著的变形与内力响应值集中于荷载作用平面内的筒体边缘处。Wang等[15]和汪嘉钰等[16]也采用离心试验对复合基础开展了动力响应分析。

目前研究中的结构设计由于忽略了对体系自振频率的控制,可能会导致地震波传递过程与实际情况有较大的差异。此外,现存的研究大多是针对海上风机单桩在砂土场地中的工况而展开的,对于桩-筒复合基础等新型基础形式的研究还不够深入。为了更好地掌握桩-筒复合基础遭遇震害后的响应规律,探究砂土地基中复合基础相对于传统单桩基础的优势与不足,基于离心振动台试验,通过输入不同地震波,开展了近海风机单桩和桩-筒复合基础的地震响应模拟研究,对比分析了砂土地基中两种基础形式的地震响应规律差异。

1 试验装置与模型设计

本次模型试验是在同济大学岩土及地下工程教育部重点实验室的TLJ-150型岩土复合离心机上进行的,试验设置的超重力场为50g,有效激震频率20～200 Hz。试验的模型箱尺寸为50 cm×40 cm×40 cm。参考单桩埋深的常见范围为20～50 m,以及小兆瓦涡轮风机的塔筒高度为15～30 m[17],本次试验模拟的单桩、柱-筒复合基础以及风电塔结构模型如图1所示,模型与原型的主要材料与尺寸参数见表1。将机舱和叶片等结构通过等质量的方式简化为添加到塔架顶部的集中铁质立方块(部件P-T和PB-T),其边长为50 mm,此等效方法可较好地等效模拟海上风电塔的机舱和叶片对基础的影响[18-23]。为对比桩-筒复合基础与传统单桩的承载性能,采用的复合基础的单桩部分(部件PB-P)横截面尺寸与单桩基础的一致(部件P-P),其桩长则被大幅缩短,复合基础的筒盖顶增设了两块环形铁板来模拟实际筒型基础的堆料设计(部件PB-W),表现出基础对浅部土层的附加应力作用(筒盖底附加应力约80 kPa)。结合本试验所用离心模型中设备与模型箱尺寸,基于离心模型的缩尺比例准则,得到如表2所示的模型试验各常数相似表。由于在实际工程中,风机的建造往往会追求在控制成本的前提下使其刚度有所保障,风机塔筒设计的自振频率通常需要依据“软-刚”原则在0.20～0.35 Hz选取。

表1 离心试验模型结构主要参数Tab.1 Parameters of centrifugal model structure

表2 离心模型试验各基本物理量相似关系Tab.2 Scale factors of parameters in centrifuge tests

图1 模型单桩及单桩-筒型基础尺寸及组成Fig.1 Dimensions and composition of model monopile and monopile-bucket hybrid foundation

本次试验中选用的模型土为福建标准砂,在此基础上混合10%粒径约0.08 mm的石英砂,以模拟原场地中分布的细小颗粒。土样颗粒的颗分曲线见图2,可以看出,干砂粒径分布较为集中。

测试得到模型土样最小干密度为1.36 g/cm3,最大干密度为1.81 g/cm3。模型砂土的填筑过程如下:干砂土体的填筑通过砂雨法来实现,以得到均匀性以及密实度可控的模型场地。本次试验落砂使用的设备为TJU砂雨装置,其落砂口为鸭嘴式,移动路径为弓字形。实际操作过程如下:首先,填筑基础底部的砂垫层,根据设定落距固定好砂桶,使出砂口与模型箱底部与出砂口距离符合落距,然后,以每层砂土2 cm厚度计,称量所需干砂质量装入砂桶内,之后,撤去堵砂装置,按照弓字形路线移动导轨和砂桶,让干砂颗粒均匀落入箱内,直到装填至最下层传感器高度时 (此时满足所填土层在纵向堆积以及颗粒排列方面都有更高的均匀性[24]),布设对应传感器并预留连接通道的导线;继续以上步骤进行填土至15 cm厚度后,定点装入单桩基础模型并校核结构顶部高度;后续重复填土及安装传感器的步骤;当装填至30 cm厚度时,定点装入筒型基础模型;最后,填土至40 cm厚度后安装结构顶部传感器及激光位移计。本试验饱和砂土地基土的制备采用同干砂模型一样的砂雨法步骤,首先,得到干砂场地,之后,利用真空饱和装置静置24 h以实现模型土层的饱和过程。由表2可知,液体渗流的时间模型比尺为N2,而动力作用时间比尺为N,由此可知在超重力环境下,场地内动力作用时间与渗流反应时间存在N倍的比例偏差。因此,在砂土饱和的过程中,采用室温条件下运动黏度约为50 mm2/s的甲基纤维素溶液(运动黏度为原型场地中渗流水的N倍)作为真空饱和阶段掺入场地内的渗流液体。

本离心振动台试验使用叠环式剪切模型箱,可以大大减轻模型箱侧壁反射地震波对基础地震响应造成的边界效应,剪切模型箱还可以较好地模拟自由场在地震作用下的真实地震反应,以较小的误差精确地捕捉如土层的加速度反应峰值和波形等数据[24-25]。为减小边界效应和两种基础的相互干扰,模型的布置过程中两基础中心沿对角线错落摆放,中心距模型箱侧壁均为15 cm(超过两倍筒径),两基础中心距约为22 cm,如图3所示。图4为试验的传感器布置。对于场地和结构的地震动响应的测量,通过加速度计可得到桩、筒基础附近土体的加速度时程,以及传递至风机顶部的加速度响应;孔隙水压力时程与分布的测量通过布设在筒型基础下方的孔压计实现;对于风机体系的变形特征,利用LVDT测得风机塔顶部在受震方向上的水平位移情况;沿单桩基础布置的双桥应变片,可测算在地震过程中单桩基础的弯矩响应。

图3 装置平面布置Fig.3 Layout of equipment

图4 传感器布置Fig.4 Arrangement of the transducers

2 试验工况设计

本次模型试验主要研究不同振幅与频谱成分地震波作用下砂土地基中两种基础的动力响应,因此,挑选了高频成分较为丰富的ACC100波与低频成分较丰富的Mexicocity波作为基岩地震动输入。两种地震波分别调幅至0.1g和0.25g作为实际输入,其中,幅值为0.1g的两种地震波波形与反应谱如图5(a)～(d)所示。

图5 输入的地震波时程及加速度反应谱曲线Fig.5 The acceleration histories and acceleration response spectrum of the input earthquake motions

离心试验中场地模型包含干砂及饱和砂两类,用以对比两种场地土层中结构物的地震响应。每种场地中进行的主要试验为以上两种地震波各两次输入的工况,因此,总体的试验工况为10组(干砂地层: Wd-1, Ad-1, Ad-2, Md-1, Md-2;饱和砂地层: Ws-1, As-1, As-2, Ms-1, Ms-2)。在试验模型装填完毕、进行主荷载施加前,对干砂与饱和砂模型均进行白噪音扫频(干砂地基为Wd-1;饱和砂地基为Ws-1),观测对比体系的自振频率。本次离心振动台试验的各工况组别如表3所示。

表3 试验工况Tab.3 Summary of the testing program

3 试验结果及分析

3.1 模型固有频率测试结果

图6为台面反馈以及A2、A4加速度计记录值转换的傅里叶谱。台面反馈图的单值波峰所对应频率值即为干砂与饱和砂情况下模型输入地震波的卓越频率,分别为3.56、3.47 Hz。土体在深部土层(埋深15 m处)出现了明显的双峰,地震波体现出了场地的特性;当地震波传递至埋深2.5 m处时,输入波的特性被显著弱化,得到的干砂场地和饱和场地的自振频率分别为1.64、1.39 Hz,后者比前者下降约15%。干砂场地中傅里叶谱为单峰谱样,而饱和场地浅层谱样在2～3 Hz附近。由于场地滤波效应出现波谷,在3.47 Hz的输入波卓越频率处仍有波峰存在,由此可知地震波在土层中传递时会积累土层的固有动力特性,干砂场地特性累积则更为明显。

图6 两种场地白噪声扫频得到的加速度傅里叶谱(水平轴为半对数坐标)Fig.6 Fourier spectra obtained by white noise sweeping (the horizontal axis is semi-logarithmic coordinate)

作为高耸结构,海上风机自身也具有较高的频率敏感性,应当关注模型自振频率是否在安全范围内。图7展示了白噪声扫频后干砂和饱和场地中两种基础顶部质量块测定的加速度进行傅里叶变化后的频谱曲线,频谱展现的一阶自振频率所在频段与地震输入波和土体自振频率所在频段相差较大,由此读取的自振频率误差会较小。根据De Risi等[26]的研究,现场风机结构设计的安全频段主要在0.20～0.35 Hz,本次试验中两种基础在干砂场地中的体系自振频率为0.329 Hz,而饱和场地中为0.313 Hz,均在安全的频率范围内,表明在本离心试验中,模型体系自振频率主要取决于出土塔筒段,受场地影响较小。

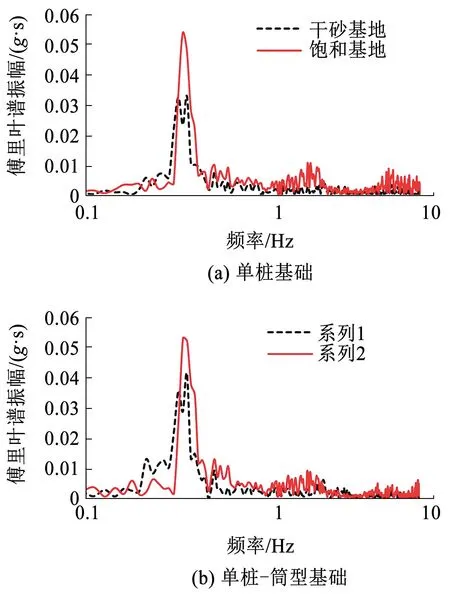
图7 两种基础顶部质量块的白噪声扫频加速度傅里叶谱(水平轴为半对数坐标)Fig.7 Fourier acceleration spectra of two kinds of foundation top masses through white noise sweeping (the horizontal axis is semi-logarithmic coordinate)

3.2 场地土层动力响应

加速度升至50g、运行平稳后,按表3中不同的工况对应施加地震波激励。图8、9为As-2和Ms-2试验组别所得到的孔压和加速度响应曲线,其中,超孔压比曲线纵坐标为超静水压力与测量点原静孔压的比值(Δu/σ′)。从图8、9可以看出,在土体深处的土体孔压不易累积,两种工况下埋深15 m处的超孔压比均未超过0.4,地震波幅值也较输入值增大。到了土层中部(地表下7.5 m处),超孔压比显著上升,As-2工况中超孔压比达到0.6,ACC100波的加速度幅值由0.265g衰减至0.188g,降幅为29.1%;对于Ms-2工况,超孔压比接近1.0,Mexicocity波加速度幅值由0.264g衰减至0.128g,降幅为51.5%。图9(d)～(f)中,在复合基础下2.5 m处,超孔压比小于0.8,地震动幅值放大至0.143g,表明接近复合基础的浅表底层范围内孔压上升受到抑制,液化现象不显著。但从图8可以看出,As-2工况中孔压显著上升至液化,加速度幅值也较深部土层进一步下降,加速度高频成分也显著弱化。

图8 As-2工况各深度处超孔压比和加速度响应(ACC100波,0.222g)Fig.8 Excess pore pressure ratio and acceleration response (ACC100 wave, 0.222g) at various depths in case As-2

图9 Ms-2工况各深度处超孔压比和加速度响应(Mexicocity波,0.232g)Fig.9 Excess pore pressure ratio and acceleration response (Mexicocity wave, 0.232g) at various depths in case Ms-2

为解释上述土层响应现象出现的原因,绘制了两种工况下的输入波频谱曲线,如图10所示。ACC100输入波卓越频率为1.39 Hz,Mexicocity输入波卓越频率为0.49 Hz,而图6(d)～(f)得到的白噪音扫频曲线表明本饱和场地在2.5 m处测得固有频率为1.39 Hz,与ACC100输入波卓越频率相近,发生了共振现象,且ACC100波在高频段仍有显著丰富的成分,因此,会导致浅部土层发生液化现象。故可推知,同一振幅水平的强震作用下,荷载频率对液化区分布有影响,7 m左右的中部土层是易液化区,但高频荷载使得浅部土层仍有液化隐患。

图10 As-2、Ms-2工况台面输入波傅里叶谱(水平轴为半对数坐标)Fig.10 Fourier acceleration spectra of output motion in cases As-2 and Ms-2 (the horizontal axis is semi-logarithmic coordinate)

3.3 风机结构动力响应

3.3.1 风机水平加速度

台面输入波幅值(APB)和结构加速度响应幅值(APR)的关系曲线如图11所示,由于土层和结构存在阻尼,风机水平加速度幅值明显小于输入波幅值。由图11可以看出,APB增大则APR也显著增大,在两种砂土地基中复合基础上质量块加速度均大于单桩基础,表明地震波沿单桩基础传递时能量耗散更多,到达风机顶部的地震强度相比复合基础更小。在同种基础形式下,饱和地基中地震波传递到结构顶部的加速度峰值更大,尤其是在强震输入的试验组别,饱和场地传递至风机顶部的加速度幅值与干砂场地差别更大,可以推断饱和砂场地土层受震弱化,基础承担的加速度比例更大,地震强度越大弱化越严重。图11(a)中ACC100波几组工况的结构地震响应随APB增大而增长的趋势较为一致;而Mexicocity波中无论干砂还是饱和砂情况,在本离心试验中,复合基础上结构加速度幅值均大于同等输入水平下的单桩基础,且荷载水平增大后风机响应差异更显著。结合3.2节,ACC100波和Mexicocity波输入到复合基础吸力筒底部的加速度峰值接近,但由于Mexicocity波卓越频率较小,更接近风机塔筒的自振频率,经塔筒传递后到达风机顶部的加速度响应强度越大,该影响在复合基础中表现更显著,且随APB增大而增强。

图11 不同工况下APB与APR的关系Fig.11 Relationship between APB and APR in different cases

3.3.2 风机结构水平位移

为比较不同工况下复合基础的水平位移响应,采用激光位移计测试了顶部集中质量块的水平位移,位移响应峰值与输入加速度峰值的关系如图12所示。对于不同的风机基础类型和工况,强震作用下的峰值位移约为小震时峰值位移的2～4倍,Wang等[15]和Rahmani等[27]的研究中对不同基础上13 m高度的风机进行50g超重力振动台试验,也得到了与本文类似的结论。从图12可以看出,同等工况下复合基础上的结构水平向位移小于单桩基础,输入加速度增加后复合基础位移峰值增加的幅度也更小,表明复合基础在结构抗水平变形方面有更好的性能。另外,在强震作用下,饱和场地中的结构水平位移明显大于干砂的情况,而单桩模型处于饱和场地时在各输入波情况下水平位移峰值也均明显大于其余工况。

图12 不同工况下APB与风机水平位移幅值的关系Fig.12 The relationship between APB and horizontal displacement amplitude of wind turbines in different cases

图13、14为ACC100与Mexicocity在强震幅输入情况下的结构水平位移时程曲线,可以看出,强震作用后单桩与复合基础上质量块均产生了自由振动,振动后结构又恢复到了平衡位置。从图13(b)、14(b)可看出,饱和场地中单桩基础上的结构在振动后产生了明显的残余位移,而复合基础的残余位移相对较小。

图13 Ad-2、As-2位移时程(ACC100输入波)Fig.13 Displacement time history of superstructure in cases Ad-2 and As-2

图14 Md-2、Ms-2位移时程(Mexicocity输入波)Fig.14 Displacement time history of superstructure in cases Md-2 and Ms-2

3.3.3 单桩的弯矩响应

单桩基础模型上粘贴应变片可测试出振动过程中模型的应变发展,以此推算出各测点的弯矩响应。为使桩身表面更加粗糙便于粘贴应变片,在模型桩表面使用砂纸沿与圆径向呈±45°的方向交叉打磨。按照图3所示在桩身外表面对称粘贴8对弯矩型应变片(BF120-3AA),其电阻为(120±0.5)Ω,灵敏度系数为2.08±0.01。为了保护应变片以及进行防水处理,在其表面及四周涂抹了环氧树脂。通过采用四分之一桥接法,将应变片连接于DH3816型应变箱上,根据式(1)通过采集到的应变片应变变化,计算得到不同深度处的桩身弯矩:

(1)

式中:EI为桩的抗弯刚度,Δε为同一桩身深度应变片的差值。

根据材料力学理论,杆件弯矩与应变呈线性关系,但实际模型中由于应变片方位、粘合剂厚度等因素会导致每个应变片对应的线性系数不同,因此,本次试验在常重力下吊装砝码施加静载,对应变片进行标定。将应变片按照从上到下依次编排为Y1～Y8,标定结果绘制于图15中,可通过标定趋势线公式对应变片所测示数开展后续弯矩换算工作。

图15 应变片示数-弯矩标定结果Fig.15 Calibration result of strain gauge indication-bending moment

经数据处理后,激振过程中单桩部分的弯矩响应包络线如图16所示,由于饱和场地试验时Y8应变片受损,未能有效监测到此处应变值。

图16 各工况下的单桩基础弯矩包络线Fig.16 Bending moment envelope of the monopile foundation in various cases

总体上看,单桩基础由浅部至深层的弯矩分布呈现先迅速减小后小幅增大的趋势,反映了深层土体对桩底的嵌固作用。随地震强度的提升,桩身的整体弯矩值明显提高。两种输入波工况下的桩身弯矩变化均表明,在小震组别,干砂和饱和砂的弯矩包络线较为接近,而大震情况下饱和场地组别的弯矩响应明显大于干砂情况,尤其是在浅部桩头处,表明土体弱化使得浅部单桩基础承担了更大比例的弯矩荷载,这也解释了图13、14中,单桩基础上风机在饱和场地组别中展示出明显残余位移的现象。

饱和试验组别各工况下浅部Y1应变片(埋深约1 m)的峰值弯矩汇总如表4所示,另将A6传感器桩周浅部土层加速度幅值也一并记录。可以看出,不同波形、同一输入强度水平的荷载传递至浅部土层后,其加速度较为接近,但Mexicocity波无论小震还是大震组别中的Y1峰值弯矩都比ACC100波的情况大40%以上。结合风机水平加速度的分析可知,由于Mexicocity波卓越频率更接近风机自振频率,风机响应更剧烈,该组别中风机传递至桩体的弯矩值也更大。