用于地下金属浅层探测的便携式频域电磁探测系统降噪方法研究
2024-01-25祁敬童汤洪志
祁敬童,汤洪志,魏 丽
(东华理工大学 地球物理与测控技术学院,江西 南昌 330013)
1 引言
目前,地下管线和地下未爆炸物质的探测对城市的建设和领域的发展具有重要意义,对这些浅层地下金属的探测和调查已成为关注的焦点[1-2]。频率域电磁测深法作为一种重要的电磁勘探方法,被广泛地应用于该领域[3]。然而,在频率域电磁探测中,近区的场分布相对复杂。除了地面波外,还存在强烈的地层波,以及由于地层的不均匀性而引起的异常场。因此,地表成为了一个含有多种成分的混合场[4]。尽管在近区存在地电异常反映,但其信号远小于作为背景场的一次场。对于通常采用测量总场来进行频率域电磁测深的方法来说,很难在总场中分辨出地电异常信息。因此,在近区进行频率域电磁测深时,如何有效地降低一次场的影响,并提取出地电异常信息十分关键。
从传感器结构上来说,传统的Turam方法利用放置在不同位置的接收线圈测量场强振幅的比率和相位差进行勘探[5],但该方法需要铺设大定源回线装置作为发射场源,效率较低。另一种电磁探测系统GEM-2通过附加补偿线圈来消除一次场,并提取磁场同相分量和正交分量进行勘探[6]。然而,该仪器起始频率较低,发射带宽较窄,采样率也较低。此外,还有一些其他的方法,如相位法、邻近频率法和组合波法等,用于一次场的消除[7],但在实际应用中仍然存在严重的一次场干扰。综上所述,当前针对一次场的消除技术仍然面临挑战,并需要进一步改进以提高效果。本文基于等值反磁通原理[8-9],提出了一种水平共轴差分线圈设计,在理论上消除了一次场的影响,充分突出异常信息。
为了在强噪声背景中检测到被噪声覆盖的微弱信号,人们进行了广泛的科研工作。这些工作包括分析噪声产生的原因和规律,研究待测信号的特点和相关性等,以寻找有效的方法来提取有用信号。在数据采集系统中,常用的工具包括低噪声前置放大器、锁相放大器、取样积分器和光子计数器等。其中,相关方法是应用最广泛的一种方法,被认为是最有效的方法之一[10]。近年来,锁相放大器作为基于相关方法发展而来的仪器,迅速兴起,并得到了广泛应用。它能够准确地检测和提取微弱信号,从而在强噪声环境下取得良好的信噪比[11-12]。然而商用锁相放大器价格昂贵,体积庞大,不便于多用户的共同使用,且硬件滤波实现的灵活性较差,升级和修改比较困难[13]。随着工程与环境勘探要求的不断发展,亟需采用新的技术方案弥补硬件滤波器的不足。本文设计了一种基于虚拟仪器技术的正交矢量型软件解调算法,用来解决这些问题。
由于仪器设备、环境和人为因素,频率域电磁数据信号在采集和传输过程中不可避免地要受到一定的影响,因此,如何消除信号中的干扰影响,并获得准确有用的数据信息非常重要[14]。传统的噪声消除方法是在噪声信号中执行傅里叶变换,然后执行逆傅里叶变换以获得“干净”信号。然而,由于低通平滑效应消除了高频干扰噪声,并且边缘变得模糊,导致一定程度的信号失真[15]。在实际信号分析中,人们总是期望得到能够代表信号性质的信息。由于信号的奇异点包含重要的信息,利用这些奇异点重构信号已成为人们关注的问题[16]。针对这些问题,本文提出了基于小波变换的阈值去噪算法,以此来提高数据质量,降低干扰对数据的影响。
2 水平共轴差分线圈设计
差分结构的一次场抑制性能可以从互感的角度进行分析。在差分结构中,第一接收线圈和第二接收线圈通过互感耦合相连。当发射线圈激励产生一次场时,这个一次场会在两个接收线圈上感应出电动势。由于差分连接方式的特殊性,第一接收线圈和第二接收线圈的电流流向是相反的。这意味着一次场在两个线圈上感应出的电动势具有相反的极性。当两个感应电动势叠加在一起时,它们会相互抵消,导致差分线圈的输出感应电动势接近于零。
2.1 发射线圈的磁场
当正弦交流信号通过发射线圈时,会在其周围产生变化的磁场,也称为一次场。根据毕奥-萨伐尔定律可以计算载流圆环在空间任意一点产生的磁场大小。在图1建立的笛卡尔坐标系中,假设半径为R(单位:m)的圆形线圈位于x-y平面上,圆心与原点重合(O点),发射线圈中通入逆时针方向交变电流I(单位:A)。这里,利用微元法求解空间任意一点的一次场强度,将圆形线圈上的电流分割成微小的一段,每一段都可以看成直线段l,并将线圈上的电流记为电流元Idl。假设电流元与x轴正方向的夹角为α,即
Idl=IRdα(-isinα+jcosα)
(1)
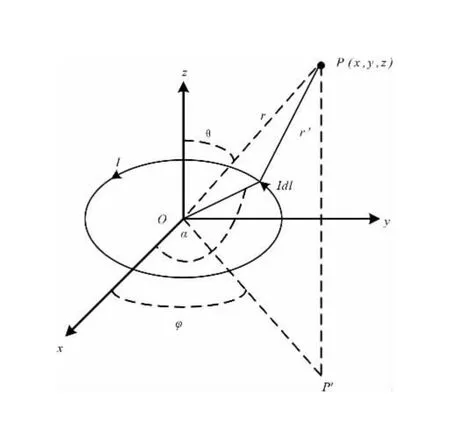
图1 载流圆线圈Fig.1 Current-carrying round coils
该电流元Idl的位置坐标为:
(2)
空间任一点P(x,y,z)可用球坐标表示为:
(3)
式中,r为圆心O点到点P的距离,单位:m。因此,由电流元Idl引向场点P的矢量为:
r′=(x-x′)i+(y-y′)j+zk
(4)
式中,r′为电流元到点P的距离,单位:m。
根据毕奥—萨伐尔定律,通电线圈在P点产生的磁感应强度B(单位:A/m)为:
(5)
式(5)中,μ0为真空磁导率,μ0=4π×10-7H/m。
2.2 差分线圈去耦合理论分析
通过建立理论模型分析差分线圈结构对一次场引发感应电动势的抑制效果。建立差分线圈的模型来进行理论分析,如图2所示,发射线圈的圆心位于坐标原点上,两个接收线圈的中心位于z轴上,发射线圈和两个接收线圈的半径均为R,发射线圈到两接收线圈的距离均为d(单位:m)。发射线圈通入角频率为ω(单位:rad/s)的正弦激励信号I=Imsinωt。其中,Im为交变电流的最大值,单位:A。
发射线圈和接收线圈a之间的互感Ma为:
(6)
其中,θ1和θ2分别为发射线圈任取一电流元与y轴的夹角和接收线圈a任取一场点与y轴方向的夹角。
根据电磁感应定律可知,由于发射线圈的一次场的作用,接收线圈a产生的感应电动势Va(单位:V)为:
(7)
同理,发射线圈和接收线圈b之间的互感Mb和感应电动势Vb(单位:V)分别为:
(8)
(9)
其中,θ3为接收线圈b任取一场点与y轴方向的夹角。
可以看出,Va=Vb,即两接收线圈由于一次场作用产生的感应电动势相等,由于两接收线圈采取的差分连接方式,所以由于一次场作用产生的感应电动势相互抵消,最后只剩下二次场而引起的感应电动势。故采取这种差分线圈结构可有效地消除一次场干扰,使得地下无金属异常时差分线圈可以处于平衡状态。
为了更深入地分析差分线圈对一次场的抑制效果,在COMSOL多物理场有限元分析软件中,分别建立了差分线圈模型和一发射、一接收线圈模型,并进行了模拟仿真。在这两个模型中,发射线圈和接收线圈的半径均为0.2 m,它们之间的距离也都是0.3 m。激励信号的频率为1 kHz,幅值为5 V。图3是模型中没有放入异常体时线圈传感器的感应输出电压。
当模型中没有放入异常体时,图3显示了两种模型的输出感应电动势。在一发射一接收模型中,输出的感应电动势是由一次场引起的,幅值接近于3 V。相比之下,差分模型输出的感应电动势接近于零,表明该结构对一次场信号具有很好的抑制效果。这进一步验证了地下无金属异常时,差分线圈处于平衡状态。
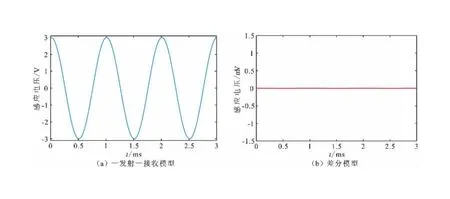
图3 线圈传感器模型输出感应电压Fig.3 Shows the output induced voltage of the coil sensor models
3 数字正交矢量解调技术
随着微弱信号提取技术的快速发展,矢量的测量越来越受到关注。在地球物理领域中,很多物理性质都是矢量解,对于传输函数、损耗因子、电导、 电容和位移电流等使用矢量测量直接得到结果是很有必要的。而正交矢量型锁相放大器用极坐标形式来表示输出信号,实现了矢量测量,且去除了相位条件的限制,避免了相位调整对测量结果准确性产生的影响,目前,已经被应用于许多微弱信号检测的场合。
3.1 正交矢量锁相放大器
锁相放大器的输出信号是由需求信号和参考信号的幅值和相位决定的,要通过输出信号来得到需求信号的幅值相位信息,就需要保证需求信号和参考信号的相位差保持恒定。保持相位的恒定加大了设计的难度,若引起相位差存在不稳定,可能会导致信号的失真和噪声的引入,从而影响测量结果的准确性。随着社会的发展,相对模拟锁相放大器,正交矢量型锁相放大器由于具有更高的精度、灵敏度、可靠性和稳定性,在科学研究和工业生产等领域得到了广泛的应用[17],并逐渐取代模拟锁相放大器,其原理框图如图4所示。
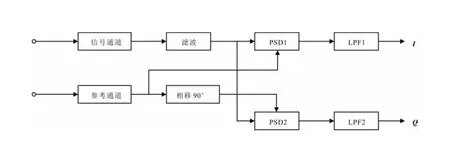
图4 数字正交矢量检测技术原理Fig.4 The principle of digital orthogonal vector detection technology
正交矢量型锁相放大器可以将被测信号和参考信号通过两个相敏检波器(Phase Sensitive Detector,PSD)和低通滤波器(Low Pass Filter,LPF)输出两个正交的分量,这两个分量分别被称为同向分量I和正交分量Q,同向分量代表参考信号与被测信号的相位相同的部分,而正交分量代表参考信号与被测信号的相位相差90°的部分,通过将被测信号和参考信号分别输送到两路通道上,可以计算出被测信号的同向分量和正交分量,进而求出被测信号的幅值和相位,也可以将幅值和相位通过计算转化成实分量和虚分量,而不需要改变参考信号的相位。与传统的锁相放大器相比,正交矢量型锁相放大器不需要对参考信号进行相位更改,相位差能够保持恒定,从而降低了对测量结果准确性的影响。
3.2 数字正交矢量解调算法
随着数字信号处理技术的不断发展更新,越来越多的硬件功能被软件所实现。基于模拟锁相放大器和正交矢量锁相放大器理论的基础核心相敏检波器,用数字微处理器替代,乘法解调法采用数字解调法替代的新型锁相放大器,即为数字锁相放大器。数字锁相放大器通过采样将被测模拟信号转换为离散的信号序列,再由上位机程序进行数字解调运算。数字解调要求控制采样频率实现整周期采样,不仅可以精确合成参考序列,而且能够建立简洁有效的数字互相关运算,其原理框图如图5所示。
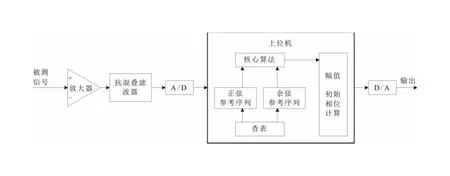
图5 数字锁相放大器算法原理Fig.5 Digital orthogonal vector software detection schematic
通过分析图5,采用模拟器件搭建数字锁相放大器的信号输入通道,对被测信号进行放大、抗混叠滤波等预处理。然后将预处理后的信号进行AD采样,得到离散序列信号输入到上位机中。而参考通道和相关器通过上位机内部编程实现。实现核心算法后进行信号幅值和初始相位的计算。核心算法过程如下:
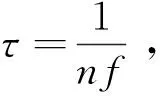
x(t)=Asin(2πft+θ)+n0(t)
(10)
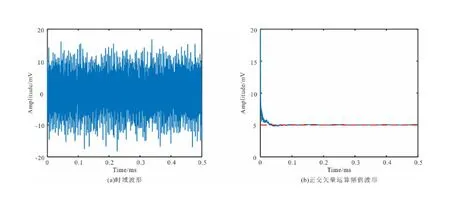
图6 加入随机噪声和工频干扰后的信号Fig.6 Signal with added random noise and power frequency interference
其中,n0(t)为噪声信号;A为被测信号的幅值。由于两个信号之间存在相干性,但与噪声信号基本没有相干性,所以在运算过程中忽略了噪声项的影响。对于经过采样后的信号序列:
(11)
其中,k=0,1,2...,Q-1。在进行数字化时,无需对参考信号进行采样,而是对其离散化,由上位机编程来产生正弦和余弦参考序列:
(12)
其中,k=0,1,2...,Q-1。经过整周期采样后的Z[k]和Y[k]序列与x[k]作相乘运算,即可得到同相和正交输出的互相关信号为:
(13)
其幅值和相位通过计算可得到:
(14)
(15)
上述过程就是一次完整的相关运算,但总的采样点数是Q个,所以需要进行Q次相关运算,然后对其作算术平均来对信号进行滤波。通过分析上述过程可以发现,只需要计算出Cx,Z和Cx,Y,就能获取被测信号的幅值和初始相位信息。以上就是数字锁相放大器核心算法原理,该算法可以用上位机软件通过编程来实现。
3.3 数字正交矢量解调算法可行性验证
在模拟平台中对正交矢量软件检测算法技术进行仿真,验证该算法的可行性,设采样频率fs=4 000 Hz,采样点数N=2 000,加入频率f0=1 000 Hz的人工模拟二次场信号x(t)=5sin(2πf0t),再加入设定的三个谐波的工频谐波干扰:n= 4sin(1 000πt+π/6)+3sin(3 000πt+π/4)+4sin(3 400πt+π/6),随机噪声加入零均值高斯分布。
将模拟二次场信号、随机信号和工频干扰信号进行叠加后的时域波形和其正交矢量运算后的幅值波形如图6所示。其中,图6 (a)中时域波形信号的最大幅值接近20 mV时,二次场信号幅值由于过小,已被噪声所淹没。图6(b)中正交矢量运算幅值波形随时间振荡衰减,衰减到一定程度时,其实际幅值向一个固定值“5”靠拢,并最终趋于稳定。
由于时域波形中二次场信号被噪声所淹没,无法直接看出原始信号的频点,因此使用傅里叶变换把时间域信号转化为频率域信号,如图7所示。
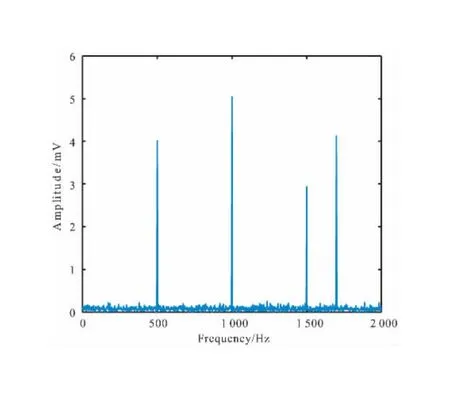
图7 频域信号Fig.7 Frequency domain signal
由图7可以很明显地从频率域信号看出原始信号的频点,使用正交矢量运算,通过正弦参考序列和余弦参考序列进行乘法运算可以分别得到同向分量I和正交分量Q,由于原始信号的初始相位为0,只需要对同向分量信号处理即可,将会得到一个直流分量,该分量包含着幅值信息。结果表明,该算法是可行的、有效的。
4 基于小波变换的阈值去噪
在软件方面,解决杂波及噪声问题涉及信号处理领域。传统的去噪方法常见的有滤波器,包括模拟滤波器和数字滤波器。除了滤波器还有傅里叶变换,FFT(Fast Fourier Transform,快速傅里叶变换)去噪不能将有用信号的高频部分和由噪声引起的高频干扰加以区分。这种情况特别是需要信号高频信息的时候就无能无力了,在去除高频噪声的同时需要保留信号高频成分。小波变换去噪可以很好地保护有用的信号尖峰和突变信号[18]。因此小波变换适合用于暂态信号和瞬态信号的噪声去除,以及抑制高频噪声的干扰,从而有效地将高频信息和高频噪声区分开。因此,小波去噪随着小波变换理论的发展也不断丰富起来,并取得了良好的效果[19]。
通过对采集信号和噪声信号的小波系数进行统计分析,选取一个合适的阈值ξ,当小波系数小于该阈值时,表示该小波系数主要由噪声信号产生,将该系数设为零;当小波系数大于该阈值时,表示该小波系数主要由真实信号产生,将这些系数按固定向零收缩或者按照原始值进行保留。综上所述,小波阈值去噪的流程如图8所示。
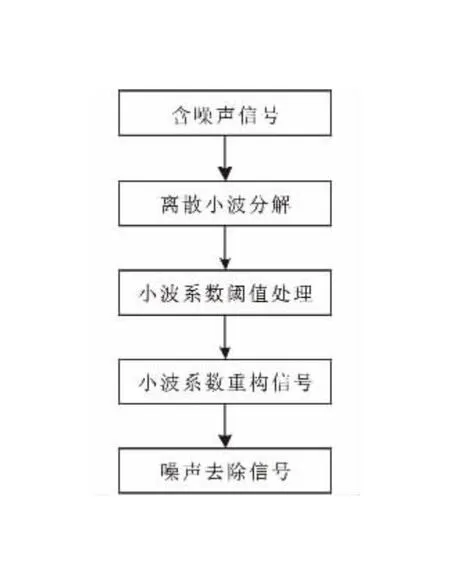
图8 小波阈值去噪流程Fig.8 Wavelet threshold denoising flowchart
从图8中可以看出,小波阈值去噪首先对含噪声信息进行离散小波分解,需要根据信号的特征选择合适的小波基及小波分解层数,采用离散小波变换得到各层的小波系数;进一步通过设定阈值和阈值函数对获得的小波系数进行处理,得到各层处理后的小波系数;最后利用处理后的各层小波系数与最后一层的近似分量进行信号重构,得到去除噪声的信号。
为了验证滤波算法的有效性和可靠性,在噪声干扰严重的实验室进行探测实验,传感器放在地面上,通过数据采集卡和上位机采集到真实数据。对于去噪结果的评价采用信噪比(Signal to Noise Ratio,SNR)和均方根误差(Root Mean Square Error,RMSE)这两个指标来评价[20],即
式(16)和式(17)中,x(t)代表采集到的信号;y(t)代表去噪后的信号;N为采样点数。其中信噪比越大,均方根误差越小,表示去噪效果越好,越接近于实测信号。

图9 总场原始电压信号Fig.9 Total field raw voltage signal
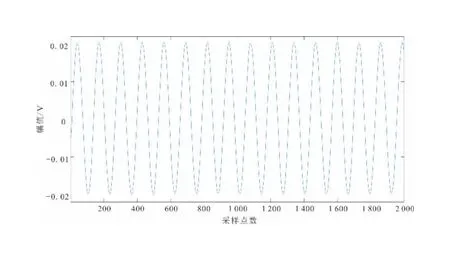
图10 三层小波变换滤波曲线Fig.10 Three layer wavelet transform filtering curve

图11 五层小波变换滤波曲线Fig.11 Five layer wavelet transform filtering curve
图9是经过探测系统采集到的总场原始电压信号。可以看出,图9中的总场原始信号曲线图夹杂着很多噪声。图10对原始信号进行三层小波分解与重建后的曲线,图11是对原始信号进行五层小波分解与重建的曲线。从图10中可以看出,该方法对于噪声信号的滤除有很好的效果,可以很好地保存有用信号的尖峰。但是对比图10和图11,小波分解与重构的层次数目并不是越多越好,也不是越少越好。因为如果层次过多,会丢失一些细节;层次太少,不能有效去除噪声[21]。对三层小波变换经过计算,信号信噪比提高了27.32 dB,均方根误差为0.006 1,该试验验证了基于小波变换的阈值去噪对信号有较好的去噪效果。
5 系统构建及实验
差分共轴便携式电磁传感器系统包含五个主要部分:空心线圈传感器、外部电容、差分放大电路、数据采集卡和上位机。传感器采用收-发线圈水平共轴差分式组合设计,其中三个共轴平行的线圈,发射线圈位于两个接收线圈之间,且与它们的距离相等。所有线圈的半径相同,而第一接收线圈和第二接收线圈以差分并联结构连接。两个接收线圈的输出端与电容器相连,形成谐振电路。谐振电路的输出端连接到差分放大电路,然后通过A/D转换器将信号采集并传输至上位机。
5.1 系统构建
频率域电磁法[22]地下金属探测系统结构框图如图12所示。具体过程如下:
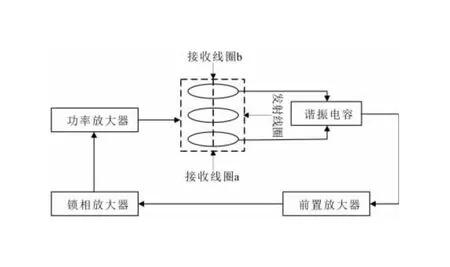
图12 探测系统Fig.12 The detection system
1)首先确定系统的工作频率,在上位机软件界面输入对应频率的正弦波信号发射和接收参数;
2)接下来软件信号发射模块提供数字信号至多功能数据采集卡,数据采集卡内的数值转换器(Ditital-to-Analog Converter,DAC)模块将数字信号转化为模拟信号,模拟信号输出至硬件发射单元;
3)该信号经发射单元内多功能数据采集卡放大电路以及运算放大器电路处理后,由发射线圈产生一次场信号;
4)差分结构的结构线圈用来抵消一次场,地下金属受一次场作用产生涡流形成二次场,此时信号采集模块通过软件强制触发而启动,此时数据采集卡控制硬件信号接收单元,采集二次场信号;
5)数据采集卡在完成采集任务后,其内的模数据转换器(Analog-to-Digital Converter,ADC)模块将采集的模拟信号转为数字信号,数字信号被上位机软件提取,软件数据存储和显示模块负责完成信号的存储和成图显示,软件信号处理与分析模块负责完成对信号的数字滤波、数字放大、小波化等相关数据处理和分析工作。
5.2 数字正交矢量滤波算法的单点实验验证
为了验证滤波算法的有效性和可靠性,在噪声干扰严重的实验室进行探测实验,传感器放在地面上,在传感器中心正上方20 cm处放置一个铁制品,使用本设备测量该铁制品的总场信号和二次场虚分量信号。图13是未经任何处理的总场原始信号曲线图,它包含噪声信号,图14是只对总场原始信号曲线图进行数字矢量正交检测技术算法提取的虚分量变化曲线图,图15是只对总场原始信号曲线图进行小波阈值滤波算法和数字正交矢量检测技术算法共同提取的虚分量变化曲线图。
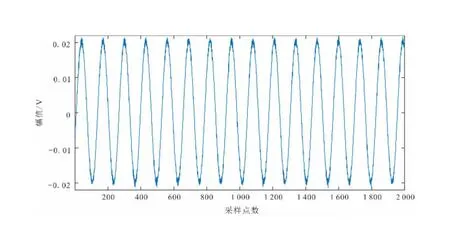
图13 总场原始信号曲线Fig.13 Overall field original signal curve graph
可以看出,图13中的原始信号曲线图夹杂着很多噪声;图14使用数字正交矢量技术对原始信号曲线图提取的虚分量异常曲线,不但可以有效地提取出虚分量,还大幅度降低了噪声,但在波峰和波谷部分曲线仍然不太平坦;图15是使用数字正交矢量技术和小波阈值滤波提取的虚分量异常曲线,它是图14效果的进一步提升,波峰和波谷部分已经变得很光滑,它结合了数字正交矢量技术和小波阈值滤波优势,可以有效地提取出更加逼近真实值的虚分量。
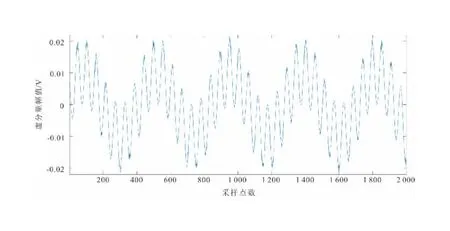
图14 数字正交矢量检测算法提取虚分量曲线Fig.14 Digital orthogonal vector detection algorithm extracting imaginary component curve graph

图15 数字矢量正交检测算法及小波阈值滤波提取虚分量曲线Fig.15 Digital vector orthogonal detection algorithm and wavelet threshold filtering for extracting imaginary component curve graph
5.3 均匀空间球体上电磁剖面实验
为了验证系统的探测效果,在实验室高噪声的环境下进行均匀空间球体上电磁剖面测量实验。测线、测点示意图和实验环境如图16所示。测线长度设计为200 cm,共有37个测点,每个测点间隔5 cm,球体异常位于中心测点(第19个测点)下方20 cm处。
本系统在进行均匀空间球体电磁剖面实验时选取的参数如下:发射频率f=1 000 Hz,驱动电压3 V,经过功率放大器对驱动电压放大后,输出电压为18 V,负载为3 Ω,不考虑阻抗,电流理论值为6 A。但接收线圈为感性线圈,对于功率放大器而言,随着发射频率的增大,线圈的感抗也逐渐增大,因此线圈内的电流会逐渐减小,发射磁矩也会减小。同时,考虑到趋肤效应和运算放大器带宽,以及多功能数据采集卡的采集速率和分辨率的综合影响,发射线圈的激励频率不宜过大。
发射频率在1 000 Hz时球体异常体二次场虚分量结果如图17所示。从图17中可以看出,在远离球体时,主要探测到的是环境的背景场,随着线圈逐渐靠近球体,二次场虚分量值逐渐增大,当线圈位于球体正上方(第19个测点)时,二次场虚分量达到了最大。其中负号只表示二次场方向与一次场方向相反,测点中二次场虚分量的幅值越高,代表二次场虚分量的强度越大。
图16 测线布置示意图Fig.16 Schematic layout of the survey line
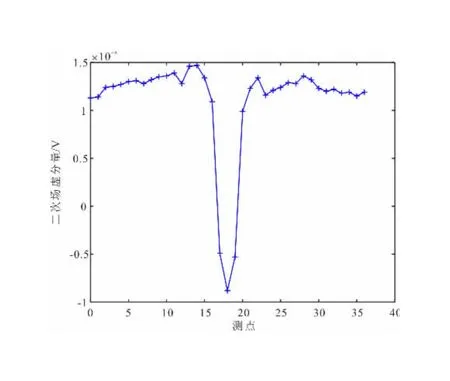
图17 二次场虚分量随测点变换曲线Fig.17 Transformation curves of secondary field imaginary components with measured points
6 结论
1)基于等值反磁通原理的频率域电磁探测技术,设计水平共轴差分线圈,在接收线圈上物理消除了一次场的影响,实现了纯二次场近源探测。
2)基于数字正交矢量解调技术,设计了数字正交矢量型锁相放大器以及相应的解调算法,该算法能将噪声中的二次场信号有效地提取出来,且能够提取电磁信号中幅值和相位信息。
3)基于小波变换技术,提出了小波阈值滤波算法来进行噪声的滤除。实验结果表明,该算法能够有效地抑制频率域电磁探测中的噪声,且将信号信噪比提高了27.32 dB。
4)进行了样机测试,通过单点和剖面探测实验,验证了本文提出的两种算法的可靠性和有效性。为后期的数据处理及实际工程应用提供算法支持。
