联合VMD和Shearlet变换的去噪方法研究

聂 荣，许辉群，赵桠松

(长江大学 地球物理与石油资源学院,湖北 武汉 430100)

1 引言

随机噪声压制是地震数据处理的重要环节,目前的方法大致分为空间域压制和变换域压制,信号与噪声在特定域中具有能够区分二者不同的特征,上述两类方法本质都是依据此特征进行信噪分离[1-2]。地震信号往往都是非平稳、非线性信号,传统的时频方法具有一定的局限性。因此,Huang等[3]在1998年提出希尔伯特黄变换(Hilbert-Huang,HHT)。其中,经验模态分解(Empirical Mode Decomposition,EMD)是HHT方法中的一个重要步骤,通过EMD将信号分解为多个本征模态函数(Intrinsic Mode Function,IMF)和一个残差信号,对IMF进行Hilbert变换可以得到瞬时信号[4-5]。近年来有大量学者对EMD方法进行改进,Wu等[6]在2009年提出了集合经验模式分解(Ensemble Empirical Mode Decomposition,EEMD)方法,一定程度上缓解了EMD分解出现的模态混叠现象;Torres等[7]通过改进EEMD方法,提出了联合互补集合经验模态分解(Complementary Ensemble Empirical Mode Decomposition,CEEMD)方法,有效地解决了EEMD加噪去除不干净的问题。EMD方法目前存在易受到噪声的影响、出现模态混叠,没有完整的数学推导等问题[8]。在2014年,Dragomiretskiy 等[9]提出变分模态分解(Variational Mode Decomposition,VMD)算法,EMD是一种递归分解的方法,而VMD与其不同,是一种完全非递归的方法,其通过不断迭代寻找出最适合的解,确定IMF分量和中心频率,因此VMD方法能较好解决EMD方法存在的问题[10]。

VMD方法能自适应地分解信号,然后通过重构IMF信号,得到去噪后的信号[11]。国内外有大量学者利用信号重构的思想开展去噪方法的研究,其中采用最多的是根据部分小波系数重构信号。例如,Mallat等[12]采用该方法对分解后的信号进行重构,获得较好的去噪结果。Donho等[13]提出先利用小波分解获得小波系数,其次将该系数依设定的阈值进行处理,最后根据处理结果获取有效数据。选择合适的阈值对小波变换处理含噪数据具有十分重要的作用,阈值如果不合适,会使小波变换处理复杂,且维度较高的数据存在一定的局限性。此外,多尺度几何分析的其他常用方法还包括：Curvelet变换[14],Ridgelet变换[15]等,这些方法在处理去噪方面已取得了较好的结果。

Guo等[16]在2007年根据紧支撑框架构造理论,提出了Shearlet变换,它具有多方向性、可稀疏表示的特性,能够较好地摆脱小波变换的局限性[17]。为提高地震资料的品质,笔者提出一种变分模态分解(VMD)和Shearlet变换联合去噪的方法,该方法通过VMD将含噪的地震信号分解为一系列频率的IMF分量,然后使用Shearlet变换对含有噪声的IMF分量进行去噪处理,最后对去噪后的IMF分量进行重构。通过合成信号与模型进行对比分析,取得了较好的结果。

2 方法原理

2.1 VMD基本原理

变分模态分解算法(VMD)能够有效地解决EMD算法中的模态混叠现象[18]。VMD具体方法如下：

1)将信号f(t)用式(1)分解为K个模态分量uk(t),uk(t)定义为一组调幅-调频信号,即

(1)

uk(t)=Ak(t)cos(φk(t))

(2)

式(1)和式(2)中,Ak(t)为振幅;φk(t)为相位函数,非单调递减,变化速度远大于Ak(t),瞬时频率为ωk(t)=φk(t)′。

2)设模态分量IMF是有限带宽的(在中心频率ωk(t)附近),则通过估计每个IMF的带宽建立带宽之和最小的变分约束公式,即

(3)

3)引入惩罚因子α和Lagrange算子λ(t),将上述问题从“有约束”变为“无约束”变分问题,如式(4)所表示：

(4)

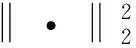
4)采用傅里叶变换,求取二次优化问题的频域解更新公式。模态函数更新、中心频率的更新和拉格朗日乘子的更新如式(5)～式(7)所示：

(7)

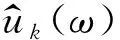
5)根据傅里叶逆变换,可以将式(5)从频域转变为时域,获得各IMF分量的时域信号uk(t)。

2.2 Shearlet变换

Shearlet变换将传统的仿射系统和合成小波理论相结合[19],通过对基函数的缩放、剪切和平移等放射变换来生成具有不同特征的Shearlet函数。当n=2时(n表示维数),Shearlet函数定义如下[17]：

(8)

式中,SAB(ψ)是合成小波;l、m、n分别表示尺度、剪切和平移参数;ψ∈L2(R2)表示合成仿射系统中的元素。W和V都是2×2的可逆矩阵,且|detV|=1。W与V分别表示尺度矩阵和剪切矩阵,其中前者主要是控制Shearlet变换的尺度,后者是控制Shearlet变换的方向。对任意w>0,v∈R,可得尺度矩阵W和剪切矩阵V,如下：

(9)

当w=4,v=1时,即

其形式就是Shearlet,w为尺度参数,v为剪切参数。

对任意(ξ1,ξ2)∈D0,令

都有：

(10)

(11)

式(11)中,l≥0,-2l≤m≤2l-1,n∈Z2。

(12)

2.3 VMD和Shearlet变换联合去噪

传统的VMD去噪方法在对地震信号进行去噪处理时,通过信号分解获得一系列频率的模态分量,将分解后的K个模态分量依据频率高低进行划分,一般认为信号中的随机噪声都处在频率较高的部分,所以在利用该方法进行去噪处理时,会将K个模态分量中的高频部分直接去除,进而致使部分含在高频部分中的有效信息丢失。鉴于上述问题,笔者提出VMD和Shearlet变换联合去噪的方法,该方法的主要内容是通过Shearlet变换对含有噪声的分量进行去噪处理,其次将去噪后的分量进行重构,最终达到去噪的目的。具体去噪流程如图1所示[20]。

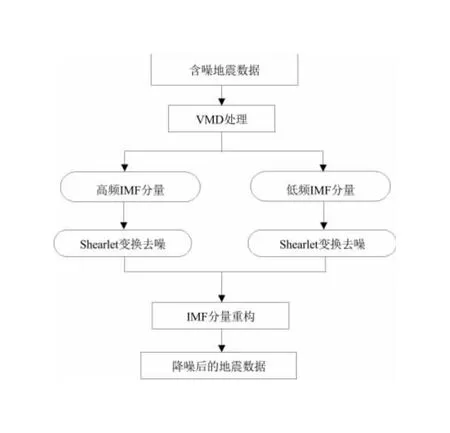
图1 去噪流程Fig.1 Denoising flow diagram

3 理论模型分析

3.1 合成信号验证

设计由10 Hz、30 Hz和120 Hz的谐波信号构成的合成信号,通过测试对VMD算法与传统EMD方法进行对比分析,验证VMD的优势所在。该合成信号由三个简单谐波信号与噪声合成,如式(14)所示[21]：

(14)

式中,t∈[0,1];ynoise表示随机噪声。图2(a)为合成信号(自上而下为10 Hz谐波信号、30 Hz谐波信号、120 Hz谐波信号、合成信号和含噪的合成信号)及其频谱图,图2(b)是EMD分解的结果及其对应的频谱,图2(c)是VMD分解的结果及其对应的频谱。在分解效率方面,VMD仅通过4个分量即分解出三个频率成分和噪声,而传统的EMD方法分解7个IMF分量(最后一个分量为残差)才将10 Hz成分完全分解(图2b中黑色框);在精度方面,VMD分解的每一个分量都准确定位了合成信号的各频率成分,而EMD分解中存在一些无效成分,由此也可证明对谐波合成信号,VMD具有明显的效率和精度优势。

上述测试结果表明,VMD去噪方法的效果相较EMD具有一定优势。进一步验证了VMD算法与Shearlet变换联合去噪方法有效性。对式(15)分别进行VMD去噪、小波去噪以及VMD和Shearlet变换联合去噪,通过重构信号及其频谱对比(图3)可知,图3(b)VMD去噪虽然较好地恢复了有效信号,但仍存在较多噪声;而图3(c)小波去噪通过自适应选取合适阈值对信号进行去噪并重构,其中虽然保留多数有效信号,使得大量噪声被去除,但同时也将高频有效信号去除;图3(d)通过VMD和Shearlet变换联合去噪,不仅去除了大量噪声,并且使得有效信号得到了极大的保护。通过信噪比值量化对比(表1),也证明该方法在抑制噪声上具有一定的优势。

图2 不同方法分解前后的合成信号及频谱Fig.2 Synthetic signal and spectrogram before and after decomposition by different methods

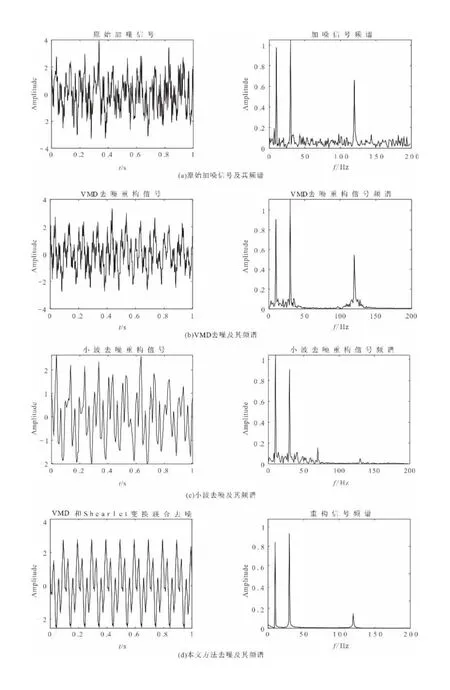
图3 不同方法去噪前后信号及其频谱对比Fig.3 Signal and spectrum comparison before and after denoising by different methods

表1 数据去噪效果对比

3.2 楔状体模型

为验证本文方法的有效性,设计如下楔状体模型(图4),该模型正演参数如下：地震子波频率30 Hz,速度分别为：2 500 m/s、2 700 m/s、2 500 m/s,密度分别为：2.2 g/cm3、2.4 g/cm3、2.2 g/cm3。

以30 Hz雷克子波作为震源子波,与反射系数褶积合成地震剖面如图4的楔状体模型(图5a为图4添加10 dB随机噪声后的正演记录)所示,采样点为120,道数120,楔状体模型的顶、底反射系数分别为0.08和-0.08。图5是模型及相关处理方法的对比图,通过对比小波去噪方法和VMD与Shearlet变换联合方法对楔状体模型处理的结果(图5b和图5c)可以看出,后者对旁瓣效应也有一定的压制。其中VMD分解的K值的确定是通过中心频率法确定,图4是由单频子波构成;图6是图5(a)中第35道和第70道数据进行VMD分解及其频谱的结果,根据该结果可以确定采用本文方法时,将K设置为2即可将单个频率和噪声分解。

3.3 实际数据测试

进一步验证该方法的适用性,对含随机噪声的实际地震资料进行测试。含噪地震剖面如图7(a)所示,该数据道数为110、采样点为401、采样时间为1 ms。通过使用VMD去噪方法(图7b)、小波去噪方法(图7c)以及本文方法(图7d)对含噪数据进行处理,根据结果的综合对比可知,采用VMD去噪方法,虽然能有效滤除部分噪声,但同时滤除了部分有效信息,使得同相轴连续性较差;相较VMD方法,采用小波去噪获得的结果较好,能滤除噪声的同时保持同相轴的连续性,但仍有部分区域存在未去除的噪声(图中黑色圈中存在较明显未滤除掉的噪声)。相较前两种方法,本文方法的去噪效果更明显,不仅能最大限度地滤除噪声,而且尽可能地保留了大量原始有效信息,同时也保持原始数据同相轴的连续性。

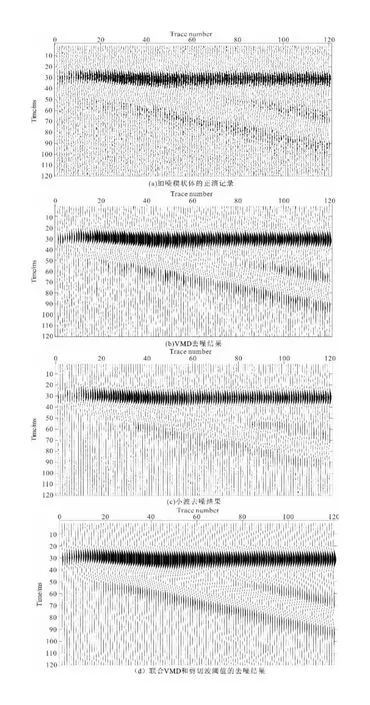
图5 加噪信号正演记录剖面对比Fig.5 Noise signal forward modeling record section comparison

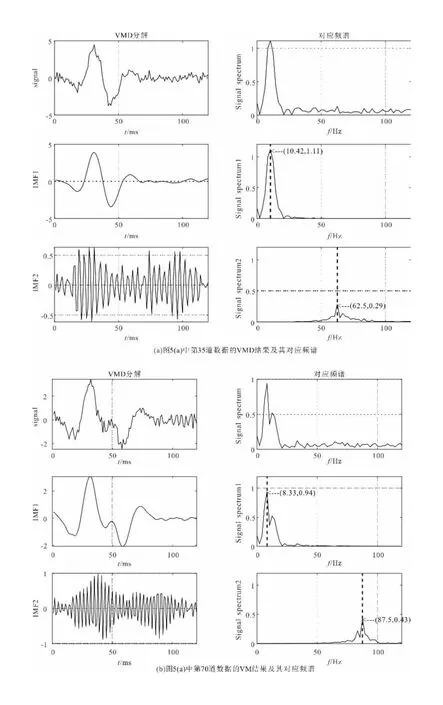
图6 图5(a)随机2道数据做VMD的结果及其频谱Fig.6 The results and corresponding spectra of VMD using two random data channels in figure 5(a)

图7 实际数据不同方法去噪结果Fig.7 Demising results of actual data by different methals

4 结论

本文构建VMD和Shearlet变换联合去噪方法,其利用了变分模态分解算法分解一系列不同中心频率分布的模态分量,避免了EMD分解过程中存在模态混叠的缺陷,然后通过具有多尺度和多方向特征的Shearlet变换,对模态分量进行噪声去除,在做去噪处理的同时尽可能保留有效信息,提高地震数据的信噪比。模型测试结果表明该方法可以去噪,且较传统方法具有一定的优势,信噪比和均方误差均可反映其效果。进一步运用实际资料证实了方法的实用性,但针对更为复杂地震地质条件的实际资料有待进一步验证方法的普适性。