组合高精度速度建模技术在渤海工区潜山成像中的应用

席自彬，王海昆，徐 强，麻志国

(中海油田服务股份有限公司 物探事业部,天津 300451)

1 引言

速度分析和速度建模贯穿于地震资料处理的全过程,是地震数据处理中工作量最大也是最关键的步骤之一[1],准确的速度场为偏移成像提供了最基础的保障。为了实现高精度的偏移成像,时间域成像往往采用多轮速度分析(人工拾取)、百分比速度扫描、十字速度调整以及偏移后剩余速度分析等多种精细速度分析方法[2]。由于常规时间偏移在横向速度处理上的局限性,对于陡倾角或者横向速度剧烈变化的区域,尤其是在潜山顶面及内幕成像、走滑断层、边界断层的成像、次级断层的接触关系不清且多解性强等区域成像,叠前时间偏移成像往往得不到精确的地下构造形态,而解决这些复杂构造区域成像的有效工具是叠前深度偏移。因此获得高精度的速度模型是提高复杂构造区域成像质量的关键一环[3]。但是如何获得高精度的速度模型,如何提高模型的精度,一直是业界广泛探讨的话题。

基于叠前深度偏移的速度建模方法有多种。一种是网格层析方法[4],2020年,徐嘉亮等[5]提出基于层位约束的不规则网格层析速度建模方法。2022年,熊鹰杰等[6]研究了基于角道集的各向异性全局走时层析反演方法。这种层析方法是线性层析,网格层析基于每一轮偏移得出成像剖面和共成像点道集,从共成像点道集上拾取剩余曲率信息,从成像剖面上拾取倾角信息,经过多次叠前深度偏移迭代,不断对速度模型进行更新。这种方法的优点是可以自动进行高密度拾取剩余曲率,不断进行迭代更新,仅耗费机时和有限的人工操作;缺点是对横向速度变化区域不敏感,反演更新效率较低,或者可能由于反演结果的不唯一性,导致速度往错误的方向更新[7]。第二种是非线性反演方法[8]。2021年,王一鸣等[9]将人工神经网络算法应用于非线性反演方法中。2022年,徐凤姣等[10]对非线性共轭梯度反演方法进行深入研究。非线性反演方法是在拾取的剩余曲率信息上进行反偏移,从而计算求得运动学不变量,不变量和速度模型叠加后进行叠前深度偏移,再求取新的曲率和倾角信息用于速度反演。这种方法的优点是反演模型精度高,对于断层等横向速度变化剧烈的复杂构造反演效果好,缺点是在每次求取不变量后都需要进行叠前深度偏移速度反演,对计算器的处理成本和处理能力要求较高,在横向速度剧烈变化区域,反演收敛较慢,增加了项目运行周期。第三种是立体层析方法[11],该方法是利用射线参数的视速度和双程的旅行时来表征目标体的相关反射。优点是该方法简单易实现,计算量较小;缺点同样是对复杂构造成像效果较差。还有一种是全波形反演[12],该方法由于需要的计算量较大,对计算器要求较高,在实际生产中很难应用[13],因此本文不做过多的讨论。

随着渤海油气田勘探开发进入以深层隐蔽型油气藏为主的阶段,潜山油气藏成为勘探开发的主要目标之一。由于原有采集和处理技术的限制,以往渤海大部分地震资料,对潜山髙陡区断层成像、边界大断层成像、潜山内幕弱信号成像的品质相对较差,无法满足勘探开发需求。常规的深度域偏移方法成像精度不高,基于逆时偏移的成像方法虽然可以解决潜山等复杂构造成像,但是不能合理利用角度和方位信息。2016年,方勇等[14]研究了多方位网格层析成像技术;2018年,蔡杰雄[15]将层析成像技术与高斯束偏移算法相结合完成针对目标的局部角度域成像方法研究。

针对上述速度反演方法和潜山区深度域成像方法的优缺点,本文在前人理论研究和实际应用的基础上,从成像效果出发,提出将组合高精度速度建模技术与射线束叠前深度偏移技术相结合的方法,基于该方法既可以兼顾好项目运行周期,提高建模效率,又可以提高建模精度,对潜山等局部速度的刻画更为精准,提高了潜山区成像质量,显著改善了潜山内幕成像,在渤海某工区潜山构造成像实例应用中取得了显著效果。

2 基本原理及技术流程

2.1 网格层析方法基本原理

网格层析反演方法是速度建模中常用的方法,因为该方法仅靠数据驱动,简单易操作,不需要其他先验信息。计算方法见下列公式[16],假设一个地下构造模型,它由不同地层构成,每一层由不同反射界面分开。计算第NL层的射线路径可以由如下的积分方程算出：

(1)

式中,SL(x,y,z)为介质的慢度;t为震源到检波器的旅行时;dl为射线路径的微分。然后计算慢度扰动以及相应层的纵坐标的扰动量,可由下式计算旅行时间的残差[17]：

(2)

Stork C等[19]给出了层析速度反演与剩余深度差的旅行时残差的定量关系,即

Δt=2×Δz×s×cosφcosγ

(3)

其中,Δz代表剩余的深度残差;Δt代表走时时差;s代表成像点位置的慢度;φ代表反射层的倾角;γ代表射线的入射角。根据式(2)和式(3)计算求得网格层析反演方程[20]。

2.2 非线性反演方法基本原理

非线性迭代反演方法原理是基于最小平方优化的反演方法,需要经过多轮的迭代来不断修正参数模型,直到最终计算数据在一定范围内能够最佳匹配的地震数据。非线性局部迭代反演方法包括梯度型方法和牛顿法[21]。拟牛顿法就是通过不断地迭代更新,近似地求取Hessian矩阵(海森矩阵)[22]来实现反演。孙银行等[23]基于各项异性参数对广义非线性反演公式进行了推导,首先构造一个目标函数：

f(C)=‖U(C)-Ud‖

(4)

其中,C代表地下参数向量;Ud代表实际地震数据;U(C)代表正演求取的模型响应。在f(C)极小值点处展开求取f(C)的二次函数：

(5)

C(k+1)=C(k)+P(k)

(6)

其中,

P(k)=-Δ2f(C(k))-1Δf(C(k))

(7)

广义非线性反演由于需要不断迭代,逐步更新逼近正确解,计算量主要在求解方程组和计算Hessian矩阵上。

Guillaume等[24]通过对拾取的剩余曲率信息和倾角信息等进行反偏移,从而获得运动学不变量,进而进行非线性反演。通过计算速度模型更新后的剩余量来实现每一次的反演迭代,对于潜山等复杂构造区,相比于网格线性层析方法,非线性反演计算收敛的速度更快,可以有效地减少迭代次数,提高迭代的精度,进而缩短项目运行的周期。

2.3 立体层析反演方法基本原理

立体层析方法是使用射线参数和双程旅行时的视速度来表征相关反射,这种方法可以不用连续拾取走时同向轴,因此更容易操作实现[25]。输入参数包括速度、入射角、反射角、反射点的位置以及反射点到炮检点的单程旅行时。

假设炮点坐标为(xs,zs),检波点坐标为(xr,zr),反射点坐标为(xc,zc),检波点的斜率和炮点斜率分别是pxr和pxs,炮点走时为ts,检波点走时为tr,朝向炮点出射角为θs,朝向检波点出射角为θr,双程反射的旅行时为tsr,地层速度为vm,则立体层析反演方法的数据分量和模型分量分别为：

(8)

(9)

在实际数据反演中,主要是求解目标函数式(9)的最优解,通过不断地修正m,使得计算模型数据d=g(m)和采集地震数据dobs一致,进而求取地层速度及成像点位置：

(10)

式中,上标T表示转置运算;Cd和Cm是数据分量和模型分量的先验协方差矩阵;mpiror代表先验模型。

2.4 组合高精度速度建模原则及思路

速度模型的更新主要有两个步骤：一是最初构建相对比较精确的初始深度域速度场;二是使用各种反演方法对速度模型进行多轮次的反演更新[26],直至深度域速度模型精确度满足需要,并达到最佳成像效果为止。

在速度反演更新的过程中,往往要遵循一定的建模原则：即从浅到深,从易到难,从低频到高频更新,从而完成由趋势速度建模到高精度速度建模的过程,趋势速度建模是通过区域速度规律研究建立纵横向速度结构趋势,而高精度速度建模是通过多尺度迭代、优化模型,修正局部速度差异。

以渤海某工区为例,本工区重处理存在以下难点：①构造地层起伏大,潜山上下速度变化快;②目标区域速度敏感、复杂断裂发育;③走滑断层及次级断层组合关系认识不清楚,潜山内幕地层速度横向变化快,速度分析难度大。针对以上地质难题及地震特征,本工区速度建模过程可细分为三步(图1)：

第一步：目标1区地震特征以浅部平层为主,该区域速度变化平缓(局部有小断层),道集质量较好,信噪比较高,非常便于拾取剩余曲率信息。该区域可以使用网格层析方法进行2～3轮反演更新,可以快速得到准确的速度场模型,缩短项目运行周期。

网格层析反演方法仅靠数据驱动,简单易操作,不需要其他先验信息。各向同性介质假设速度修正时,直接对共反射点道集(Common Reflection Point Gather,CRP)拾取剩余曲率信息,利用网格层析成像技术修正深度层速度体,因此处理时选择合适的剩余曲率谱是提高反演速度和精度的关键。本文主要通过对偏移后道集进行切除处理,去除同向轴远端畸变影响,同时限定剩余曲率谱拾取范围,以获得准确的剩余曲率,提高反演的精度。

图1 渤海某工区数据按地震特征目标细分Fig.1 Data classification of a working area in Bohai according to their seismic characteristics

第二步：目标2区为潜山区或者边界大断层区域,道集质量稍差,信噪比较低,速度横向变化复杂,所以要先对偏移道集进行信噪比提高和多次波衰减等处理,提高道集质量品质,该区域使用非线性反演方法更新,可以得到高精度速度模型。

对于潜山等复杂构造区,相比于网格线性层析方法,非线性层析反演收敛的速度更快,可以有效地减少迭代次数,提高迭代的精度,进而大大缩短项目运行的周期。在此基础上,本文采用多参数控制的混合模型更新方法,首先从共成像点道集(Common Imaging Gather,CIG)上拾取剩余曲率信息和各项异性参数体,从叠加剖面上拾取X、Y方向的倾角信息,在计算时加入求取的X、Y方向的倾角信息数据体、各项异性参数体以及剩余曲率等约束信息,并对多种参数更新迭代,进一步提高了潜山成像的精度。

第三步：目标3区位于潜山内幕,通过道集拾取速度更新困难,或者局部构造层析反演尺度无法刻画相应的速度变化,道集上很难判断速度趋势,而且该区域不是成像的目标区,因此该区域使用速度扫描立体层析方法进行更新,可以减少计算成本,提高速度建模效率。

本文使用射线参数和双程旅行时的视速度来表征相关反射,可以不用连续拾取走时同向轴,因此该种方法更容易实现操作。

综上所述,针对该工区的特点进行速度建模,思路如图2所示。

3 潜山构造区应用效果分析

3.1 建立深度域初始速度模型

建立初始速度模型的方法有很多种,既可以由时间域的叠加速度、偏移速度和剩余速度来建立,又可以由井数据来建立。基本过程是先把时间域均方根速度转换成深度域层速度,然后进行大尺度的平滑,平滑的目的是消除所有短波长异常,最后由长波长(大尺度)向短波长(小尺度)迭代,逐步收敛来逼近真实速度模型。因此,初始速度模型是否足够准确对偏移结果至关重要,平滑的速度在迭代过程中更安全,但是做平滑处理时要综合考虑断层、潜山等复杂地质构造区域的特征。速度模型也不能太过平滑处理,特别是在整个项目周期有限的情况下,因为这时的初始速度模型如果太过偏离,在次数有限的更新迭代情况下,不可能实现速度模型的快速收敛,从而无法获得精确的速度场[27]。

初始速度模型的建立是深度偏移的关键环节,层速度模型一般由叠前时间偏移(Pre-stack Depth Migration,PSTM)均方根速度转换得到,较为准确的初始深度层速度模型会使后续工作更加高效。一方面,可获得高质量的深度偏移道集和成像剖面;另一方面,反演时能够快速地收敛、减少迭代次数,快速地逼近正确的速度模型,既可以缩减项目周期,又可以取得精确的成像剖面[28]。

本次初始速度模型的建立流程如图3所示。第一步,利用叠前时间偏移得到的均方根速度转换成时间域层速度(图3b);第二步,时间域层速度转换成深度域层速度(图3c);第三步,对深度域层速度存在的奇异点进行编辑及平滑,并进行海底1 500 m/s水速充填,完成初始模型的建立(图3d)。

3.2 网格层析反演方法更新浅层区速度

在初始速度模型建立以后,以此为基础,需要进一步通过三维网格层析反演,在每一个网格点(50 m×50 m×5 m)上进行速度更新,通过2～3轮的更新迭代来解决长波长和短波长的速度更新问题[29]。三维网格层析反演是基于三维网格点进行有限差分模型修正,是对3D速度体进行的网格点模型修正。对于地下构造,若速度真实、正确,在同一个共成像点道集上,不同偏移距位置处的同向轴是平的,即地下同一位置处,一定会产生同样的地质成像[30]。若同相轴向上弯曲,则偏移速度低于真实速度;若同相轴向下弯曲,则偏移速度高于真实速度[31]。因此CIG道集上的剩余曲率可以用于速度模型修正。层析反演即根据剩余曲率及地层倾角信息,在全数据体修正更新模型。层析反演更新速度后,可以准确地调整模型中短波长速度场的误差,得到更精确的深度层速度模型[32]。

浅层速度模型采用网格层析反演技术更新,使用的是全部地震数据(也可称为数据全驱动反演),采用叠前深度偏移(Kirchhoff或者Cbeam)得到深度域CIG和叠加剖面。基于CIG拾取剩余曲率,基于叠加剖面拾取X、Y方向的倾角,开展三维层析反演更新深度-层速度体,剩余曲率和X、Y方向的倾角拾取网格一致,均为50 m×50 m×5 m。经过2～3轮更新,CIG剩余曲率逐渐变小,速度变得精确。从图4可以看出,速度模型更新后,浅层道集基本拉平,剩余曲率谱比较聚焦。图4能量谱中,颜色越深,代表越聚焦,红色处剩余曲率(基本为零),得到的浅层速度谱比较精确。

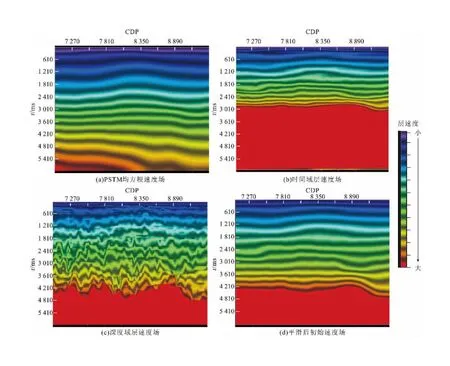
图3 初始速度建模流程Fig.3 Initial velocity modeling process

图4 网格层析前后浅层道集和曲率谱变化Fig.4 Changes of shallow track collection and curvature spectrum before and after grid tomography

3.3 非线性反演方法更新潜山区速度

对于潜山内幕速度的更新,由于潜山处道集质量太差,速度模型更新前需要对道集进行合适的预处理。如图5所示,主要包括去噪(提高信噪比)、多次波衰减、适当地切除等,进一步提高道集质量,确保剩余曲率拾取的准确度。

图5 潜山区道集处理过程Fig.5 Gather processing in buried hill location

道集处理后,针对目的层位,潜山内幕速度的更新采用非线性层析反演技术,建模流程分五步骤：①首先对速度模型进行叠前深度偏移;②从CIG道集上拾取剩余曲率信息和各向异性参数体,从叠加剖面上拾取X、Y方向的倾角信息;③对拾取的剩余曲率信息、各项异性参数以及倾角信息进行反偏移,求取运动学不变量;④对运动学不变量叠加输入的速度模型重新进行叠前深度偏移处理,生成新的曲率谱和道集;⑤如果道集基本拉平,即剩余时差(Residual Time Difference,RMO)最小,则输出为最终模型;如果RMO不是最小,采取新一轮反演更新。非线性层析反演采用多参数控制的混合模型进行更新,速度建模更新精度高,迭代次数少。

图6为非线性反演前后速度模型,从图6可以看出,非线性反演后速度模型与地质吻合度更好,精度高,能够很好地刻画复杂断裂。

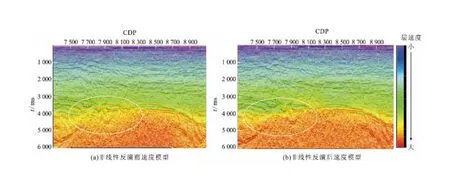
图6 非线性反演前后速度模型Fig.6 Velocity model before and after nonlinear inversion

3.4 速度扫描的立体层析更新潜山内幕区

经过线性和非线性速度模型更新后,已经可以得到较好的背景速度趋势,为了对潜山内幕进行更加精准地成像,对于基底以下背景速度进行速度扫描,如图7所示。由于基底下地层对速度不敏感,可能相差较大的两个速度(如4 800 m/s或者5 000 m/s)都可以使道集拉平,这个时候使用CIG道集拉平原则将不能准确地对基底下速度进行判定。可基于参考线成像剖面和井速度的综合考虑,通过不同速度地扫描,选择合适的背景速度。从图7可以看出,潜山内幕速度为5 000 m/s时,边界断层处同向轴更加连续,成像效果更好。

图7 基底下不同速度的叠加Fig.7 Stack of different velocities under the substrate

图8 最终速度模型及与井资料对比Fig.8 Final velocity model and comparison with well data

3.5 总体效果对比

通过针对不同目的层采用不同组合的反演技术,经过多轮更新后,可以得到高精度的速度模型,同相轴平整能量团更加聚焦集中,道集更平,叠加剖面上构造形态更加清楚和聚焦。如图8所示,从速度模型与地震资料叠合来看(图8a),速度变化与地震剖面吻合度更高。从井资料来看,反演后最终速度(图8b蓝色)与井资料VSP速度(图8b黄色)一致。

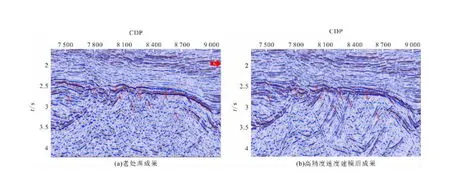
图9 高精度速度建模前后的叠前深度偏移剖面Fig.9 Prestack depth migration profile before and after high precision velocity modeling

图10 高精度速度建模前后的叠前深度偏移时间切片Fig.10 Pre-stack depth migration time slices before and after high-precision velocity modeling

将最终成果与老处理成果进行新老处理对比(图9,图10)以检验本次处理的效果。老资料采用常规速度建模方法进行Kirchhoff叠前深度偏移,本次新处理采用组合高精度速度建模进行射线束(Cbeam)叠前深度偏移。通过分析对比图(图9)可以看出：

1)新处理资料的信噪比大幅提高;

2)潜山顶面及内幕成像效果大幅提高,尤其是潜山内幕小断层有了明显改善,潜山内幕波组特征清晰,视分辨率更高;

3)浅中层花状断层改善明显,地层接触关系更明确,多次波压制更干净。

从图10时间切片也可以看出,经过高精度速度建模以后,对于中深层成像效果改善明显,潜山及边界大断层刻画得更加清晰、准确。

4 结论

通过对不同目的层使用组合高精度速度建模技术的研究及实际处理应用,可以得出以下结论：

1)组合高精度速度建模技术的有效使用可以同时兼顾项目运行周期和速度建模精度两方面要求,在大幅提高建模效率的同时,可相应地提高速度建模精度。本文提出的方法可在地震数据处理中广泛使用。

2)对于浅层以水平层为主的区域,使用网格层析速度建模方法,经过2～3轮反演更新,可以较快速地得到精度较高的速度模型;对于中深层潜山构造区,使用非线性反演方法,迭代收敛的速度更快,速度模型更加精确、稳定,有利于提高潜山构造成像精度;对于潜山内幕及基底下成像,使用速度扫描的立体层析方法,综合考虑井速度和成像剖面,可以获得合适的背景速度。