基于CMIE与参数优化KELM的旋转机械故障诊断策略*
2024-01-25伍永豪
连 璞,吴 磊,伍永豪
(1.长治职业技术学院 机械电子工程系,山西 长治 046000;2.西安交通大学 机械工程学院,陕西 西安 710049;3.联合传动及轴承技术研究中心,宁夏 石嘴山 753000)
0 引 言
旋转机构在工业制造、航空航天、医疗设备、机器人、自动化生产线等领域有广泛的应用。其结构组成非常复杂,因此容易发生故障[1]。当旋转机械发生故障后,需要先确定故障的部位,再采取相对应的措施。旋转机械的振动传递路径非常复杂,振动信号中包含大量与故障特征无关的成分,需要采用可靠的方法提取高质量故障特征[2-3]。
目前,针对旋转机械的故障特征提取,以熵值为代表的非线性动力学分析方法应用较为广泛。
KUAI M等人[4]将排列熵与自适应噪声完备经验模态分解相结合,将其用于齿轮箱的故障诊断,结果证明了排列熵作为故障表征指标的有效性;然而排列熵忽略了信号的幅值信息,降低了故障特征质量。为增强排列熵对幅值的敏感性,研究人员做了大量的工作,并取得了不错的效果。ZHOU Sheng-han等人[5]提出了加权排列熵,并将其用于滚动轴承的故障诊断,结果证明了加权排列熵的有效性;然而加权排列熵在分析某些信号时仍然会丢失幅值信息。XUE Shao-hua等人[6]基于均方根对排列熵进行了改进,提出了改进排列熵,并通过实验验证了这种改进方式的有效性;然而改进排列熵会丢失信号的频率信息,使分析不够全面。随后,LIU Xiao-feng等人[7]提出了增长熵,医学时间序列的分析结果表明,在性能上增长熵要优于排列熵。
然而上述分析方法只进行了信号的单尺度分析,无法全面地表征信号的动态特性。
为实现排列熵的多尺度分析目的,武哲等人[8]提出了多尺度排列熵(multiscale permutation entropy,MPE),将其用于齿轮箱的故障诊断,结果验证了MPE相对于单尺度排列熵的优越性;然而MPE的粗粒化对信号长度依赖较大,通过计算得到的熵值具有较大的偏差,并丢失了特征信息。随后,蒋玲莉等人[9]提出了自适应多尺度排列熵方法,齿轮的故障诊断结果表明了该方法的有效性;然而其依然未考虑信号的多个尺度特征。董治麟等人[10]优化了粗粒序列的构造方式,提出了复合多尺度排列熵(composite multiscale permutation entropy,CMPE),将其用于滚动轴承的故障诊断,结果表明了CMPE性能要优于MPE;然而CMPE依然忽略了信号的幅值信息。
在故障识别方面,极限学习机(extreme learning machine,ELM)具有优异的学习能力和计算效率,然而输入权重和隐含层阈值的随机设置会降低模型的稳定性。为此,HUANG Guo-bin等人[11]使用核函数代替ELM中的随机映射,提出了核极限学习机(KELM),KELM的分类性能和泛化性相较于ELM有了明显的增强;然而KELM的参数也需要进行预先设置。赵小惠等人[12]利用粒子群算法优化KELM的参数,实现了对齿轮箱故障进行准确识别的目的;然而粒子群算法的优化性能不佳。李琨等人[13]采用鲸鱼算法对KELM进行了改进,采用该算法能够准确识别液压泵的故障;然而鲸鱼算法的局部寻优能力有待提高。
针对上述问题,笔者提出基于复合多尺度增长熵(CMIE)和算术优化算法优化核极限学习机(AOA-KELM)的旋转机械故障诊断方法。
首先,笔者利用CMIE提取振动信号的故障特征;随后,随机抽取部分故障特征对AOA-KELM进行训练;最后,将测试样本输入至完备的分类器中进行故障的识别,利用齿轮箱和滚动轴承故障数据集对基于CMIE和AOA-KELM的故障诊断方法开展实验验证和分析。
1 复合多尺度增长熵
1.1 多尺度增长熵算法
多尺度增长熵(multiscale increment entropy,MIE)算法避免了增长熵(increment entropy,IE)只进行信号单一尺度分析的缺陷,使分析结果更加完整[14]。其求解步骤如下:
1)对于分析信号{x(i),i=1,2…,N},构造多个粗粒序列,公式如下:
(1)
式中:s为尺度因子;
2)计算每个尺度s下的增长熵值,得到所有尺度因子的增长熵,如下所示:
(2)
式中:IE为增长熵;m为嵌入维数;R为量化分辨率。
在MIE方法中,粗粒信号的长度依赖于分析信号的长度。因为粗粒信号的长度等于原信号的长度与尺度因子的比值,随着尺度的增加,粗粒信号的长度也随之减小,导致粗粒信号包含的信息无法完全表征信号的固有特性。
1.2 复合多尺度增长熵算法
CMIE采用复合粗粒化来改进传统粗粒化的不足。在每个尺度上,CMIE构造多个复合粗粒序列;然后,计算每个粗粒序列的增长熵值;最后,计算每个尺度增长熵的平均值来生成复合多尺度增长熵。
其具体原理如下:
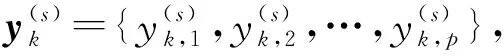
(3)

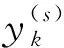
(4)
为了直观地对比传统粗粒化处理和复合粗粒化处理的区别,笔者以尺度因子为3时的粗粒化为示意图进行说明。
尺度因子为3时的复合多尺度增长熵和多尺度增长熵的粗粒化过程,如图1所示。

图1 尺度因子为3时的复合多尺度增长熵和多尺度增长熵的粗粒化过程Fig.1 The coarse-grained process of composite multiscale increment entropy and multiscale increment entropy when scale factor is 3
由图1可以发现:MIE经过粗粒化处理后只生成一个粗粒化序列,而CMIE在经过粗粒化后能生成3组粗粒序列。CMIE采用的复合粗粒化处理对信号长度的依赖性大大降低,尤其是在尺度因子较大时,复合粗粒化序列能够较为全面地保留信号中所蕴含的故障信息[15]。
1.3 仿真实验分析
为了说明数据长度对性能的影响,笔者分别选择数据长度为1 024、2 048、3 072、4 096、5 120、6 144的高斯白噪声和1/f噪声进行CMIE分析。
不同长度高斯白噪声和1/f噪声的CMIE如图2所示。

图2 不同数据长度噪声的CMIEFig.2 CMIE for noise of different data lengths
由图2可知:随着数据长度的增加,增长熵值的分析结果趋于稳定。观察图2(b)可知:在数据长度为N=1 024时,熵值曲线存在跳变点,分析结果不够精确,误差较大,如果需要获得更加可靠的结果,则需要增加分析数据的长度。
通常而言,数据长度越大,则分析的效率也就越低。因此,综合考虑效率和精度,笔者选择数据长度为N=2 048进行后续的分析。
此外,为验证CMIE的优越性,笔者分别计算20组高斯白噪声和1/f噪声的CMIE、MIE、CMPE和MPE均值和标准差。
CMIE和MIE的参数设置为:嵌入维数m=2,量化分辨率R=4,尺度因子s=20;CMPE和MPE的参数设置为:嵌入维数m=5,时间延迟d=1,尺度因子s=20。
两种噪声信号的CMIE、MIE、CMPE和MPE均值标准差如图3所示。
由图3可以发现:CMIE和CMPE熵值曲线较为平缓,波动较小,证明熵值在各个尺度上较为稳定。两种方法都采用了复合粗粒化处理方式,对数据长度的依赖降低,避免了随着尺度因子的增加而误差明显增大的缺陷。
CMIE各个尺度的标准差均小于CMPE,证明CMIE方法具有优异的稳定性。
对于CMIE和MIE方法,CMIE曲线的标准差显著小于MIE曲线,证明了采用复合粗粒化处理能够获得更加精确的分析结果,优于传统的粗粒化处理。总之,CMIE方法在分析非线性信号时能够获得较为精确和稳定的结果。
2 AOA优化KELM
2.1 核极限学习机
核极限学习机(KELM)是在ELM的基础上,将随机映射替换为核函数映射。它可以有效地削减运算的复杂度,提高模型的精准度和鲁棒性[16]。
假定训练样本(xj,tj)有M个,而xj=[xj1,…,xjn]T∈Rn,tj=[tj1,…,tjm]T∈Rm,ELM为了保证预测的精准性,使得输出的偏差最低,即存在输入层与隐藏层的权值ωi,输出层与隐藏层的权值βi,第j个隐藏层的偏置bi,使得:
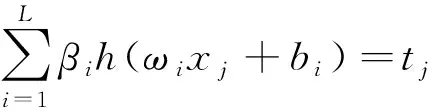
(5)
式中:h(x)为激励函数。
上式可通过隐藏层输出向量H和期望输出向量T进行简化,如下所示:
Hβ=T
(6)
ELM基于最小范数最小二乘法,生成输出权重β,如下:
β=H*T
(7)
式中:H*为H的广义逆矩阵。
将参数I/C引入至ELM中,以达到增强算法鲁棒性的目标,则有:
(8)
因为ELM的惩罚系数C会随机赋值,导致输出结果不稳定,笔者利用核函数K(xi,xj)代替HTH,则KELM的输出定义为:
(9)
式中:ΩELM为核矩阵,定义如下:
(10)
笔者采用径向基函数(radial basis function,RBF)作为KELM的核函数进行分析,RBF函数定义为:
(11)
式中:σ为核函数。
2.2 AOA优化KELM的流程
KELM通过引入核函数,增强了其分类识别的稳定性,也使得算法对参数更敏感。
为了进一步增加KELM分类器的稳定性和性能,笔者采用算术优化算法(AOA)对KELM的核参数σ和惩罚系数C进行优化搜索,建立AOA-KELM分类器模型。
算法优化算法(AOA)是一种基于数学中的四则混合运算思想而提出的智能优化算法,乘除运算提高了算法的全局优化性能,而加减运算提高了算法的局部寻优性能。其相关理论已在各种优化问题中进行了应用[17-19]。
AOA-KELM的具体流程如下:
1)初始化AOA优化变量的维度、种群大小,加速函数的最大值和最小值、允许的迭代次数、局部开发准确度和调整搜索阶段的控制指标;设置KELM的核参数和惩罚系数的优化范围;
2)随机建立种群,初始坐标代表核参数和惩罚系数的初始值,以训练样本的识别错误率最小为优化目标进行求解;
3)判断初始种群是处于搜索阶段或是开发阶段,随后对初始种群坐标进行更新;
4)对坐标更新后的种群进行适应度比较,将适应度值最小所对应的种群坐标视为最佳,并判断是否达到允许的迭代次数;
5)将迭代完毕所获得的最优解赋予给KELM,进行模式识别。
3 基于CMIE和AOA-KELM的诊断方法
针对旋转机械[20-21]的故障特征提取与模式识别,笔者提出了一种基于CMIE和AOA-KELM的旋转机械故障诊断方法。
该故障诊断方法的具体流程如下:
1)采集旋转机械多组工况下的振动信号,分割成长度为2 048的多组样本;
2)利用CMIE提取样本的熵值信息,构建故障特征向量;
3)随机选取样本对AOA-KELM进行训练,剩余的样本用于构建测试集;
4)利用训练完的模型对测试样本进行测试,根据分类器的输出结果评估旋转机械的故障类型。
4 滚动轴承实验数据分析
4.1 实验数据
为了验证基于CMIE和AOA-KELM故障诊断方法的有效性,首先,笔者利用凯斯西储大学的轴承数据进行实验。
轴承型号为SKF 6205,采集信号时轴承的负载为1.47 kW,利用电火花在健康轴承上分别加工出0.177 8 mm、0.355 6 mm、0.533 4 mm的单点故障,传感器布置于电机驱动端附近,并以12 kHz的频率采集振动信号。
笔者以转速1 750 r/min下采集的轴承振动数据为分析样本,构造了10个轴承工况下的分析样本,包含不同的故障类型和故障程度。
10种工况样本的详细信息如表1所示。

表1 轴承样本的详细信息Table 1 Bearing sample details
对于每个工况,笔者将其平均分割为50个不重叠的长度为2 048的样本,随机选择每个工况的25个样本进行训练,其他25个样本作为测试样本,以此来验证基于CMIE和AOA-KELM的故障诊断方法的性能。
10个轴承工况数据样本的时域波形如图4所示。

图4 轴承信号的波形Fig.4 Waveform of bearing signal
4.2 特征提取
根据图4的波形可知,振动信号具有较大的随机性,难以用其提取信号的信息差异[22-23]。
为了更好地表征信号的复杂度,提取能够代表故障频率的特征,笔者采用CMIE方法提取滚动轴承的故障特征,结果如图5所示。

图5 振动信号的CMIE均值Fig.5 CMIE mean of vibration signal
由图5可以知:B2和NOR样本的熵值小于其他样本,证明CMIE方法能够较好地区分这2种工况。其他8个工况的熵值曲线具有一定的重叠,无法直观地判断特征的可区分度。
后续笔者将结合分类器模型进一步验证基于CMIE和AOA-KELM故障诊断方法的有效性。
4.3 模型诊断评估
笔者将CMIE的20个熵值作为故障特征向量,同时将25个训练样本输入至AOA-KELM分类器进行训练,剩余25个样本进行测试。
测试样本的故障识别结果如图6所示。

图6 基于CMIE的AOA-KELM诊断结果Fig.6 Diagnosis results of AOA-KELM based on CMIE
从图6可知:仅有一类样本被错误分类了,即2个B1样本被错误地识别为O1样本,因此B1样本的识别准确率为92%,而其他9类样本的识别准确率为100%;模型总的诊断准确率为99.2%。
4.4 实验评估
4.4.1 分类器对比实验
为了验证分类模型的有效性,笔者采用粒子群算法(particle swarm optimization,PSO)、遗传算法(genetic algorithm,GA)、灰狼算法(grey wolf optimization, GWO)、网格搜索算法(grid search,GS)对核极限学习机进行优化,建立相应的KELM最佳模型,并进行故障的识别。
笔者分别记录每种分类器的识别准确率、分类时间,实验结果如表2所示。

表2 不同故障分类器的识别结果Table 2 Identification results of different fault classifiers
从表2可以发现:GA-KELM的准确率最低,为95.6%,同时其分类效率也较低,需要10.08 s进行故障识别;而AOA-KELM分类器的准确率最高,达到了99.2%,同时分类效率也最高,只需要3.14 s,综合性能最优。
因此,AOA-KELM分类器在滚动轴承的故障识别中具有优异的性能,且优于其他四种分类模型。
4.4.2 不同熵值方法的对比实验
为了验证CMIE方法的性能,证明其在故障诊断中的应用潜力,笔者分别采用MPE、MIE、CMPE和复合多尺度加权排列熵(composite multiscale weighted permutation entropy,CMWPE)进行对比实验,分别利用四种方法提取轴承振动信号的20个熵值特征,并采用AOA-KELM进行故障的识别,如图7所示。

采用基于CMIE和AOA-KELM的故障诊断方法和另外四种方法得到的故障诊断结果以及特征提取时间,如表3所示。

表3 各模型的详细诊断结果Table 3 Detailed diagnostic results for each model
由图7和表3可知:CMPE和CMWPE均取得了100%的识别准确率,高于CMIE方法的准确率,证明CMPE和CMWPE方法都能够准确地识别滚动轴承的故障类型和严重程度,具有一定的应用价值。
CMPE和CMWPE方法的特征提取时间分别为433.33 s和489.47 s,远高于CMIE方法的提取时间190.11 s。
因此,基于CMIE和AOA-KELM的故障诊断方法具有非常可观的效率,同时准确率也比较高。
总之,CMIE在具有极高效率的同时,也具有不错的准确率,优于其他几种方法。
为进一步验证CMIE、CMPE和CMWPE方法在故障识别中的性能差异,评估三种方法的可靠性,笔者将不同数量特征依次输入到AOA-KELM分类器进行识别,其结果如图8所示。

图8 三种诊断方法输入不同数量特征的准确率 Fig.8 The accuracy of three diagnostic methods when input different number of features
由图8可知:在输入不同数量特征时,CMIE的曲线处于CMPE和CMWPE曲线的上方,这证明在输入不同数量的特征时,CMIE的准确率普遍更高。而当输入的特征数量大于16个以后,三种方法的准确率曲线相差不大。
因此,CMIE方法、CMPE和CMWPE方法的性能差距较小,但是CMIE方法在特征数量较少时要优于另外两种方法。
5 齿轮箱实验数据分析
5.1 实验数据
为了进一步验证基于CMIE和AOA-KELM故障诊断方法的有效性,笔者利用QPZZ-II机械故障模拟实验台采集的齿轮箱数据进行实验分析。
实验平台如图9所示。

图9 齿轮箱故障模拟装置Fig.9 Gearbox fault simulator
该平台由驱动电机、轴承、齿轮箱和制动器组成,笔者将缺陷齿轮替换健康齿轮来模拟齿轮箱的各类故障,同时更改制动电流来模拟负载的变化。
振动信号的采样频率为5 120 Hz,电机转速为880 r/min,制动电流为0 A,笔者记录了五种齿轮箱故障状态数据。其中,每种状态的振动数据被分割为50组长度为2 048的信号序列,共250组样本。
具体的数据信息描述如表4所示。

表4 齿轮箱样本的数据信息Fig.4 Gearbox sample data information
5.2 模型诊断和评估
首先,笔者利用CMIE方法提取齿轮箱振动信号的故障特征,结果如图10所示。

图10 振动信号的CMIE均值Fig.10 CMIE mean of vibration signal
由图10可知:CMIE具有一定的区分度,没有出现较大的混叠或者交叉,证明CMIE提取的故障特征能够较好地表征齿轮箱的各种故障状态。但同时直接观察CMIE熵值曲线无法判断样本的故障状态,需进行进一步的处理。
随后,笔者将故障特征输入至AOA-KELM分类器进行故障的识别,得到的诊断结果如图11所示。

图11 基于CMIE的AOA-KELM诊断结果Fig.11 Diagnosis results of AOA-KELM based on CMIE
由图11可知:基于CMIE和AOA-KELM的故障诊断模型取得了99.2%的识别准确率,有1个样本W被错误地识别为样本B,其他样本都被准确地识别出来。这表明该模型能够完成齿轮箱故障的精准识别工作。
随后,为了验证基于CMIE和AOA-KELM的故障诊断模型的优越性,笔者对在滚动轴承实验中取得了良好结果的三种方法进行了分析。其中,在熵值方法方面(CMIE、CMPE和CMWPE),在分类器方面(AOA-KELM,GS-KELM和GW-O-KELM),对不同的混合故障诊断模型进行了对比实验,结果如表5所示。
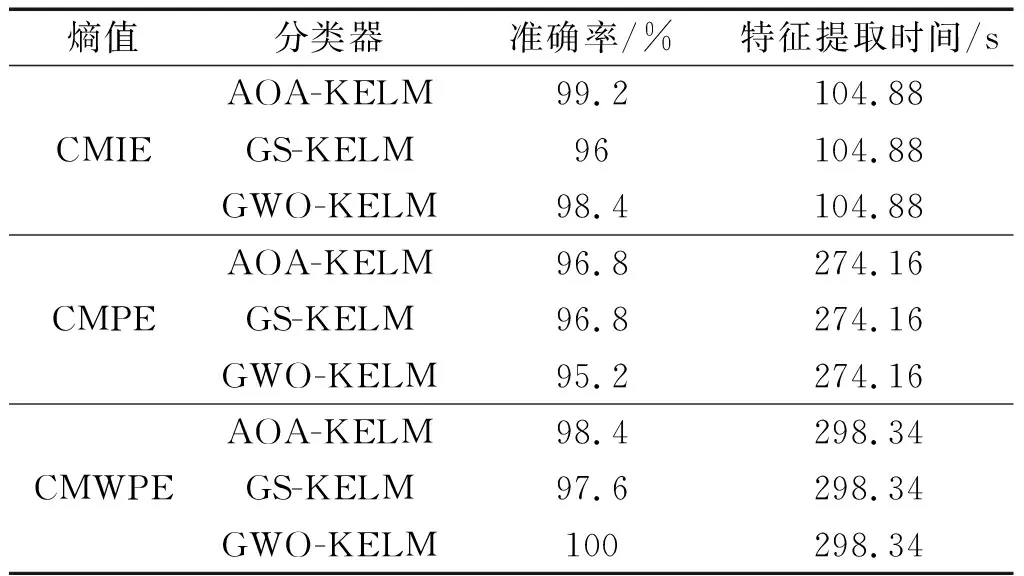
表5 不同故障诊断模型的诊断结果Table 5 Diagnosis results of different fault diagnosis models
由表5可知:CMIE结合AOA-ELM在分类准确率和效率方面具有最优的结果,虽然CMWPE结合GWO-KELM具有100%的识别准确率,但特征提取时间较基于CMIE和AOA-KELM的故障诊断方法多出了193.46 s,效率较为低下。
综合上述分析可知,基于CMIE和AOA-KELM的故障诊断方法具有一定的优越性。
6 结束语
针对现有旋转机械故障诊断方法的诊断准确率较低导致模型可靠性不佳的缺陷,笔者提出了一种基于CMIE和AOA-KELM的旋转机械故障诊断方法,利用两组旋转机械故障数据集进行了实验,证实了该方法的有效性和应用潜力。
研究结论如下:
1)CMIE在测量时间序列的复杂度方面优于CMPE和MIE方法,其具有更小的误差和更高的准确度;
2)CMIE结合AOA-KELM的分类准确率为99.2%,优于GA-KELM、GWO-KELM、GS-KELM、PSO-KELM模型,CMIE结合GS-KELM和GWO-KELM的分类准确率分别为96%和98.4%,因此,AOA-KELM的分类性能更优;
3)CMIE结合AOA-KELM能够有效地识别旋转机械的故障类型,分类准确率均达到了99.2%以上,同时在特征提取效率上优于CMPE和CMWPE特征提取模型,综合性能更加优异。
基于CMIE和AOA-KELM的故障诊断方法在分类过程中依然存在错误识别的样本,后续笔者将就进一步提高该方法的分类准确率展开研究。
