基于字典学习的舌诊图像去噪研究
2024-01-25刘为相李灿张霞周作建宋懿花
刘为相,李灿,张霞,周作建,宋懿花
(南京中医药大学,江苏 南京 210000)
在生物医学工程、神经网络和多种优化算法的不断发展和完善下,人工智能已经进入了临床诊断的范畴。舌诊所需的图像可利用模式识别等算法进行处理,使中医舌诊的发展进入了一个全新的阶段,大大促进了中医舌诊客观化、规范化的进程,对中医舌诊的继承与创新有举足轻重的作用。在量化研究中,最常用的是RGB(红绿蓝)模型,不同类型舌诊影像RGB数据存在差异,说明利用电脑影像技术进行舌诊客观化分析是切实可行的,但是现有的舌象处理技术中,大多以[1]RGB模型为基础对舌象颜色值的修正,而在舌诊图像去噪方面没有相关研究。
K-SVD(K-Singular Value Decomposition)算法是目前最具有代表性且应用领域最广泛的自适应学习字典算法。MALLAT首先提出了图像的超完全信号稀疏表达,利用Gabor词典对图像进行稀疏表示,并将其用于图像稀疏表达。稀疏和冗余表示技术是目前信号和图像处理领域的一个主要的研究领域,包括稀疏搜索、图像锐化、字典构造、人脸图像压缩、图像去噪、图像修补以及图像尺度放大等研究领域。由此提出基于字典学习算法对中医舌诊图像降噪的研究,并分别通过单层字典去噪及深度字典去噪两种方式做出对比,放大实验效果[1]。
1 数据集预处理
预处理部分包括对比度拉伸、直方图均衡化、空间平滑滤波以及空间锐化滤波,流程见图1。其中空间平滑滤波包括均值滤波以及中值滤波,空间锐化滤波包括Sobel算子以及Laplacian算子。
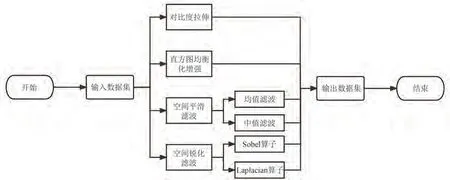
图1 数据集预处理流程图
2 稀疏模型构建
假设原始样本为Y,字典矩阵为D,原子为dk,稀疏矩阵为S,矩阵乘法为DX。字典学习的主要思想是利用包含K个原子dk的字典矩阵D∈Rm×K,稀疏线性表示原始样本Y∈Rm×n(其中m表示样本数,n表示样本属性),即有Y=DS(最理想情况)[2],其中S∈RK×n为稀疏矩阵,上面的问题可以被用数学语言表示为下面的最优问题:
上式中,S为稀疏编码的矩阵,si(i=1,2,…,K)为该矩阵中的行向量,代表字典矩阵的系数。‖si‖0表示零阶范数,它表示向量中不为0的数的个数[3]。
式(1)的目的函数表达式是为了尽量减少查找到的词典和原始样本之间的误差,也就是尽量恢复原来的样本;它的限的制条件‖si‖0≤T0,表示查字典的方式要尽可能简单,即X要尽可能稀疏。式(1)或式(2)是一类具有限制的最优化问题,它可以通过拉格朗日乘子方法进行求解。
注:将‖si‖0用‖si‖1代替,主要是更加便于‖si‖1求解。
在此,有两个最优变量D,S为了求解该优化问题,通常会将一个最优变量固定,然后对另外一个最优变量进行优化,这样交替进行。接下来稀疏矩阵可以S利用已有经典算法求解,如Lasso(Least Absolute Shrinkage and Selection Operator)、OMP(Orthogonal Matching Pursuit)。其中以更新字典D为例:
假设X是已知,逐列更新字典,当仅更新字典的第k列时,记dk为字典D的第k列向量,记SkT为稀疏矩阵S的第k列向量。那么对式(1)有:
因此,需要求出最优的dk,skT[4]。这是一个最小二乘问题,它可以用最小二乘法来解决,也可以用SVD法来解决。但不能用Ek进行求解,否则求得的新的skT不会被稀疏化。因此需要将Ek中对应的skT不为零的位置提取出来,得到新的Ek。假设需要更新第0列原子,需要将skT中为0的位置找出来,然后把对应Ek的位置删除,得到E'k,此时优化问题可描述为
因此求得最优的dks’kT。
取左奇异矩阵∪的第一个列向量u1=∪(·,1)作为dk,即dk=u1。取右奇异矩阵的第一行向量与第一个奇异值的乘积作为x‘kT,即s‘kT=∑(1,1)VT(1,·)。得到S‘kT后,将其对应地更新到原SkT。
3 字典学习算法
稀疏模型剔除了大部分的冗余变量,仅保留了最接近于反应变量的解释变量,从而使模型更加简单,但又能保持最关键的信息,从而解决了许多问题。由此可发现,稀疏模型所达到的效果与字典学习的目的一致,都是要将冗余的无关紧要的信息删除;而将重要的、本质的信息得以保留[5]。也正因如此,“字典”的衡量标准也就随之产生,字典创建的好与坏主要取决于它这个模型够不够稀疏(也就是说提取的特征是否足够关键,是否足够本质)[6]。
3.1 单层字典学习算法去噪
首先进行对Patch切块的函数定义:通过np.copy(data)将数据载入,随后定义Patch的边长及patch_size=8。其次完成对形状及数据类型的定义shape=(9,620 01,8,8),dtype=np.float32。之后确定对共9张图片进行处理,每张图片大小为(256,256),通过定义所有行的每1格标注一次,再进行每1列的每格标注一次,由此完成对切块函数的定义。
高斯噪声单层去噪:首先使用高斯噪声训练字典。根据zscore的规范化方法,将数据中的数据除以平均除以方差。然后,对MiniBatchDictionaryLearning类进行初始化,并根据初始参数对类别进行初始化。
完成上述步骤后开始绘制V中的字典:
利用figsize方法指明图片的大小,4.2英寸宽,4英寸高。其中一英寸的定义是80个像素点。循环画出100个字典V中的字(其中n_components是字典的数量)。Enumerate()函数通常在 for循环中使用,把一个可遍历的资料物件合并成一个索引序列,并列出资料和资料下标。
随后6个参数与注释后的6个属性对应,left,right,bottom,top,wspace,hspace分别对应(0.08,0.02,0.92,0.85,0.08,0.23)此时已完成从高斯噪声的图像中提取字典并准备开始高斯噪声的稀疏表示。
通过differents=[]得出复原图片和原图的误差,transform_algorithms为字典表示策略。
接下来先通过调用remove_files()函数清空此文件夹中之前的文件,然后利用set_params()函数来设定第二个相位的参数。transform是基于set_params来建立一个已设置的参数的模型的词典,它代表了一个code中的结果。code共有100个栏,每个栏都对应一个V中的词典单元,而所谓的“稀疏”是指代码中每个行的大多数元素都是0,因此可以用最小的词典元素来表达。
随后用code矩阵乘V得到复原后的矩阵patches及样本(62 001,64)=稀疏表示(62 001,256)*过完备字典(256,64)。这一阶段结束还原数据预处理:patches +=gaussian_mean,将patches从(62 001,64)变回(62 001,8,8)。随后通过reconstruct_from_patches_2d()函数将patches重新拼接回图片。以psnr_score作为复原图片和原图的误差计算并得出,最终展示去噪复原图并重命名完成保存。
椒盐噪声单层字典去噪方式与上述相同,不再赘述。
3.2 深度字典学习算法去噪
基于深度学习的降噪技术是当前图像处理中的一个热点问题。在此基础上,设计了对应的网络结构,获取了关键特征,并对输入和输出的对应关系进行了研究。在完成一定数量的图像采样后,可以得到充分的信息,如图像特征、数据分布等信息,隐含去除噪声,达到去除噪声的目的,原理见图2。本研究中的深度学习为两层网络层。在输入图像过后,在对图像进行降噪处理时,采用了卷积运算,抽取有用的特征,并采用非线性映射进行判断推理,并采用判别式学习方法获得图像降噪前的信息,达到了对噪声的分离[7]。

图2 深度去噪原理图
其中,卷积神经网络(CNNs)是最典型的深度学习类降噪算法,而CNNs则是一种改进的DNNs结构,也就是LeNet网络的5级结构,并在分类工作中脱颖而出。之后的研究通过对图像数据的存储和运算的限制,改进了LeNet的网络架构,并在ImageNet的比赛中,通过GPU训练出8个层次的AlexNet,它的分类精度提高了11%。
二者均属典型CNN,CNNs结构的主要构成元素为负责抽取主要图像特征的卷积层(Convolution layer),同时加上激活函数(Activation function)的非线性映射作用可以加快网络的收敛速度。当前,在深度学习的研究中,大量标准化技术也被用于加快网络的训练。将这些功能各异的网络层结合起来,可以构造出不同层次的网络,从而完成复杂的图像处理[8]。
①卷积层。它是CNNs与其他神经网络的一大特色,其主要作用是对多个卷积核进行卷积,从而实现对图像的局部特征的提取。卷积运算实质上是对相应的位置要素进行加法运算,在一个CNNs中,有多个纵深的卷积层,每个卷积层内都有若干个不同的卷积核,因此可以进行多个卷积运算。与粗略地进行一次卷积运算不同,多层多次的卷积运算不但能提取出较浅的区域内的图像特征,并且可以从图像中提取出更深层次的语义特征。如果卷积层是一个矩阵卷积层,那么它就是一个特操作不但可以提的特征图,而卷积且还层则是一个特殊的特征映射,但是它也是矩阵形式。在卷积运算完成后,每个卷积层都会通过一个具有非线性近似功能的激活函数,并把新的特征映射结果输入到下一层次。
②池化层和完全连通层。在具体的任务环境中,并不是所有的特性信息都能起到很大的作用,所以池化层的功能主要是筛选重要的特征数据,过滤掉多余的数据,增强了网络的普遍性。最大池是最大池和平均池,通常使用最大池方法来保持较高的纹理信息。在CNNs中,全连接层通常在网络的末尾,但在网络的最终输出端。全连通层是将各层的各节点与各层的节点连接起来的,所以在这一层中,所有的特征信息都集中在一起,从而能够集成分布的特点。然而,由于全连接层的存在,会产生许多冗余的参数,因此,目前通常都是以卷积层或池化层来进行网络性能的优化。
③激活函数。为了增强网络的逼近能力来模拟任意复杂的函数,一般在线性卷积操作之后使用激活函数强化神经网络的学习能力,常用的激活函数有四类:Sigmod,Tanh,ReLU,Leaky。ReLU函数是当前深度学习中应用最为频繁的一个非线性激活函数,它具有简单、高效的特点,能够有效地解决深度学习中的梯度消失问题。ReLU的函数表达式为:F(x)=max(0,x)。实验采用了ReLU和Sigmoid作为激活函数,配合完成深度去噪。首次定义dico1时将字典的数量即n_components定义为144,当再次进行第二层卷积时,将dico2的字典数量定义为256,通过两次卷积完成深度字典学习。
4 成果展示及分析
4.1 数据集介绍
当前有效的深度降噪算法多为有监督学习,要求对输入输出的图像进行采集(Noisy/noise-free images pairs)建立数据集合是一个重要的工作。数据的质量是影响降噪效果的重要因素。如何尽可能多地采集到大量的影像资料,并得到高品质的参考影像(ground truth)是当前的一个重要课题。本课题数据集来自江苏省中医院,该数据集收集了来自不同患者的阴虚证和非阴虚证舌诊图片,数据集涵盖500个样本,每个样本均包含了舌诊图像和对应的临床标注信息。在数据预处理中,对舌诊数据进行了预处理及对应的噪声去除,统一提升了舌诊图像质量。
4.2 评价方式
对去噪实验结果利用峰值信噪比(PSNR)的值进行比较,其中利用到diff、MSE以及PSNR[9]。为了衡量经过处理后的影像品质,通常令其结果与原图像进行对比。PSNR计算公式为:
其中,MSE为两个m*n单色图像I和K残差值的平方,I为无噪声原图像,K为I的噪声近似,MSE计算公式为:
4.3 结果
在采集过程中,数字图像中的高斯噪声是最主要的来源。传感器的噪声是因为光线不好或温度过低所造成的。在图像处理中,利用空间滤波技术可以有效地消除高斯噪声,但由于图像的平滑会造成图像的边缘和细节的模糊。常用的降噪方法主要有平均(卷积)滤波、中值滤波、高斯平滑[10]。
实验对椒盐和高斯噪声对应的深度和单层字典去噪结果做了组内和组间对比,见表1、图3、图4,对比标准为PSNR值。结果就组内而言,单层字典学习对舌象去噪有效,且深度字典学习去噪对舌象去噪效果要优于单层字典学习去噪。组间对比发现,字典学习算法对高斯噪声去噪的效果无论是单层还是深度都优于对椒盐噪声的去噪。

表1 PSNR值对比表

图3 高斯噪声去噪展示图

图4 椒盐噪声去噪展示图
5 小结
实验选取了中医舌诊图像去噪作为研究对象,结合当下热门的字典学习算法(KSVD)领域,通过主动添加噪声对比在不同情况下单层字典学习和深度字典学习所展现出的不同的去噪能力,并辅以对比度拉伸、直方图均衡化等功能对舌诊图像进行预处理。本实验以中医舌诊图像去噪方法实现作为研究对象,研究了字典学习算法对于不同情况噪声的舌诊图像去噪能力的不同,从而减少外部条件对舌诊图像产生影响,并将影响尽量降低,以此来辅助到医师的舌诊功能,助力中医事业的发展。
