激光诱导放电等离子体极紫外辐射的模拟*

王均武 玄洪文4)† 俞航航 王新兵 Vassily S.Zakharov

1) (广东大湾区空天信息研究院,广州 510700)

2) (华中科技大学武汉国家光电研究中心,武汉 430074)

3) (凯尔迪什应用数学研究所,莫斯科 125047)

4) (中国科学院大学,北京 100049)

1 引言

极紫外(extreme ultraviolet,EUV)光源是半导体集成电路制造中光刻机的重要部件[1],激光诱导放电等离子体(laser induced discharge plasma,LDP)[2]是产生极紫外光源的重要技术手段之一.LDP 由放电等离子体(discharge produced plasma,DPP)结合激光等离子体(laser produced plasma,LPP)发展而来.LDP 光源通过简单地提高电能注入便可以提升极紫外光的输出功率[3],早期作为曝光光源在极紫外光刻的商业化应用中崭露头角,如Philips Extreme UV 公司应用在ASML 公司NXE3100 系列样机上NovaTin 光源就是基于LDP 技术[4].2010年以后,随着激光器性能的提升,LPP 光源的转化效率大幅度提升,而LDP 光源转化效率的提升遇到了瓶颈,导致LDP 技术在曝光光源上的应用逐步被LPP 技术所取代.然而LDP 有着结构简单、成本低、能量转化率高等优势,在掩膜检测、显微成像、光谱计量等方面依然具有重要应用[5].例如,Ushio 公司基于Xtreme 公司的LDP 技术开发出TinPhoenix 系列检测光源[6],该光源已于2019年投入掩膜检测的商业应用中[7].

基于LDP 的模拟被各研究机构采用,以提高EUV 的输出功率和转化效率[8].2008年Hassanein等[9]采用HEIGHTS 软件对LDP 进行模拟,研究发现放电过程中箍缩产生两个EUV 辐射区[10].2012年,Zakharov 等[11]采用程序Z* code 模拟发现短电极间距有助于提高EUV 的辐射强度.2010年,Sasaki 等[12]模拟发现激光功率密度对LDP-EUV辐射有着主要影响.2010年,Masnavi 等[13]理论计算发现LDP 光源的最佳等离子体温度、密度分别在30 eV,1018cm–3左右.2016年,Tsygvintsev 等[14]模拟发现在LDP 的电流上升初期和中期分别存在Z 箍缩和微箍缩两种机制,两者共同影响EUV的产生.2016年,Beyene 等[15]采用Z* code 对皮秒和纳秒激光诱导圆盘电极放电进行模拟,该研究发现皮秒激光诱导放电形成的等离子体的温度、轴向速度、电导率和电离度均要高于纳秒情况,EUV辐射功率更强.

尽管国内对Z 箍缩驱动的放电等离子体特性[16,17]开展了较多研究,但是对LDP 的动力学模拟研究较少.而LDP 的设计相比LPP 能涉及到放电电压、电极结构等更多参数,采用模拟的方法可以为LDP-EUV 光源搭建中参数优化提供指导.因此,本文首先建立一个精确的全局状态方程(equation of state,EOS)以及不透明度的数据库,并以此为基础构建辐射磁流体模型,重点分析了LDP 的动力学特性对极紫外辐射特性的影响.

2 数值模型

本文LDP 模拟主要计算流程如图1 所示.首先,基于原子结构程序计算不同价态锡离子能级结构以及跃迁谱线的振子强度;其次,基于热力学模型计算低温EOS,结合碰撞辐射模型计算离子组分,计算高温EOS,建立全局EOS、电离度、不透明度等数据库方便后续计算查询;然后,加入激光以及电流烧蚀靶材模型,完善边界条件;最后,采用辐射磁流体力学(radiative magneto-hydrodynamic,RMHD)模型,求解等离子体动力学特性和EUV 辐射特性.本模型和国际上相关模型的差异在于其具有更为细致的等离子体辐射特性、电离和状态方程、激发率和电离率以及等离子体动力学系数计算,考虑了相对论效应对原子结构的影响、非热平衡对辐射传输的影响.

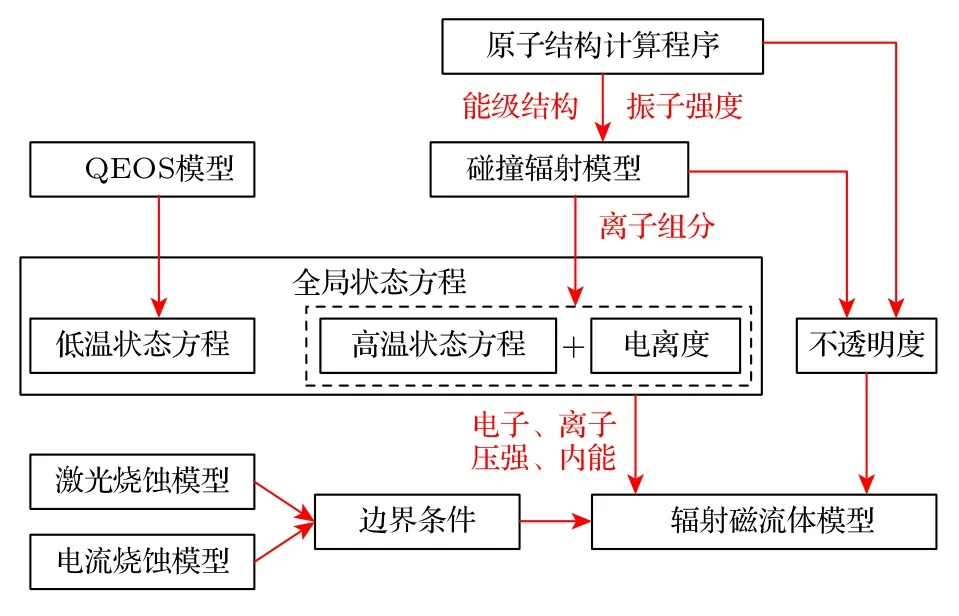
图1 激光诱导放电等离子体及其极紫外辐射磁流体模拟流程图Fig.1.Flow chart of radiative magneto-hydrodynamic simulation of LDP and its EUV radiation.

2.1 辐射磁流体模型

二维辐射磁流体程序采用俄罗斯KIAM 机构开发的Z*code[18].该程序基于欧拉-拉格朗日隐式差分格式对自洽电磁场耦合辐射输运方程求解[19],等离子体的流体动力学过程由电子和离子的质量、动量和能量守恒方程表现,如下式所示:

这里,ρ 是等离子体密度,v是离子速度,u是电子与离子速度差,c为光速,Te,i为电子、离子温度,j为电流密度;pe,i是电子、离子压力,等离子体总压力p为电子、离子压力之和,εe,i为电子和离子的内能,由EOS 数据库插值求得;是离子黏度,可以由(1)式—(7)式计算;Pv为人工黏度系数,其中L为计算网格尺寸,U为二阶张量,电子黏度忽略;Qei表示电子-离子碰撞能量交换,是电导率,是电子、离子的热导率,We,i表示电子、离子热流,G是外部热源,主要代表激光能量沉积.空间电磁场的演化由麦克斯韦方程组和广义欧姆定律表征,具体表示为

这里,ne表示电子密度,e为电子电荷量.

电磁场满足边界条件: 放电轴上Bφ(0,z,t)=0,Er(0,z,t)=0;电极表面∂Bφ/z=0∂,其中φ,z,r分别代表电磁场的的环向、轴向和径向分量.辐射能流密度Fr可由辐射传输方程(13)和方程(14)求解[20]:

其中,下标ω 代表光波频率;Iω,jω,kω分别为频率ω 光波的辐射强度、发射率、吸收率,由不透明度表插值求得;Ω是辐射方向上的单位矢量.

考虑激光沿任意给定轨迹的吸收和反射,利用简化的双向传输光线追踪模型计算了激光的输运,具体表达式为

这里,ψ+和ψ–分别为正向和反射光的能流密度,s是光线传输路径矢量,总能流密度ψ=ψ++ψ–;激光吸收系数κl包括逆轫致吸收系数κst,共振吸收系数κr,电离吸收系数κbi以及激发吸收系数κbb;激光反射系数rl由激光频率ωl和等离子体频率ωpe计算获得,根据激光吸收系数和总能流密度可计算沉积等离子体的激光能量G.

电流烧蚀靶面等离子体特性由真空电弧模型求解[21].假定阴极表面的电流均匀分布,阴极表面的电流密度为j=I/(πR2),R是阴极表面等离子体的径向尺寸,I为放电电流.初始等离子密度为

其中,γ为靶材的烧蚀率,固体锡靶的烧蚀率为300 μg/C,jz为轴向电流密度,vz为电极表面等离子体法线方向上的初始膨胀速率,M为锡原子质量,初始平均电离度和等离子体温度参考实验值[22].

2.2 全局状态方程模型

EOS 表征不同温度、密度条件下等离子体中电子、离子各自的压强、内能、熵等参数.由QEOS模型[23]可知,等离子体的自由能F(Ti,Te,ρ)由电子热贡献项Fe(Te,ρ)、离子热贡献项Fi(Ti,ρ)以及零温自由能F0(ρ)组成[24]:

其中电子热贡献项由Thomas-Fermi 模型计算[25],离子热贡献项由Cowan 模型计算[26].该模型在高温稀薄等离子体区域采用理想气体状态方程,忽略了电离与激发对内能的影响,采用碰撞辐射模型[27]取代理想气体状态方程进行修正.在碰撞辐射模型中,相邻两价态离子数密度NZ和NZ+1满足:

式中,S(Z),αr(Z+1)和α3b(Z+1) 分别代表Z价离子的碰撞电离速率系数以及Z+1 价离子的辐射复合、三体复合速率系数,这些系数可以由下面的半经验公式求解[28]:

其中,EZ表示Z价离子的电离能,ξz表示Z价离子最外层电子数.考虑等离子体密度带来的电离能降低效应,采用 Debye-Hückel 模型[29]对电离能修正,得到不同温度、密度下锡等离子体内各价态离子分布以及平均电离度如图2 和图3 所示.

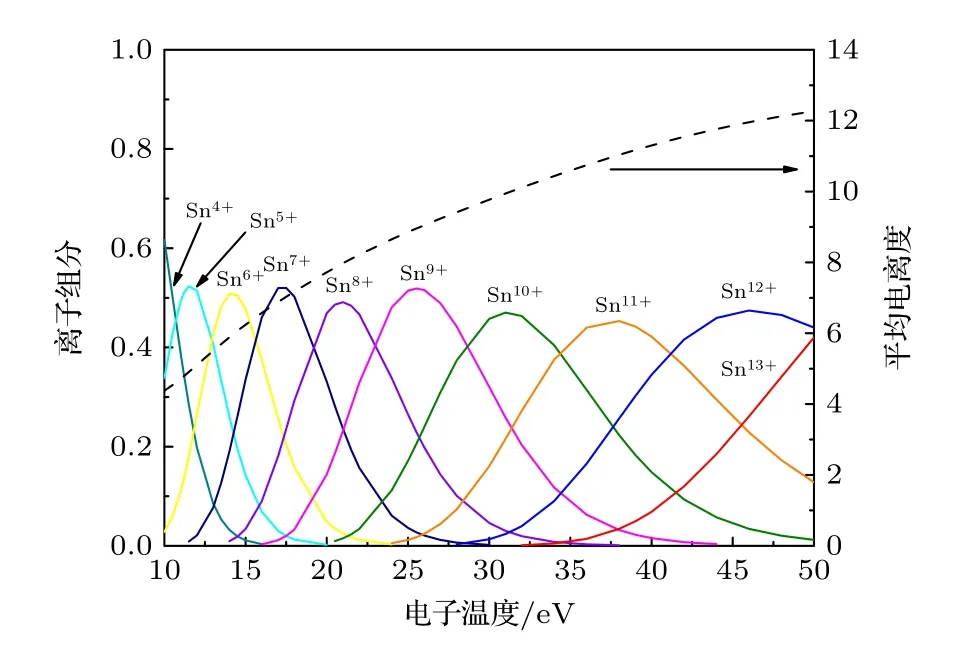
图2 电子密度为1020 cm–3 时,不同电子温度条件下锡的离子组分以及平均电离度Fig.2.Charge state distributions,average ionization degrees of tin plasma at different electron temperatures when ne=1020 cm–3.

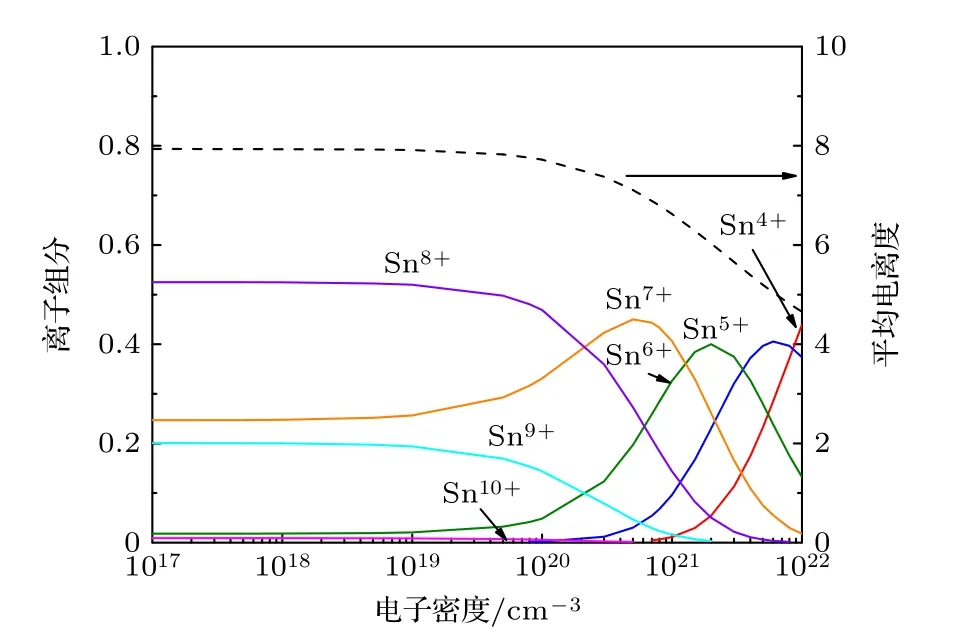
图3 电子温度为20 eV 时,不同电子密度下锡离子的电离态分布以及平均电离度Fig.3.Charge state distributions,average ionization degrees of tin plasma at different electron densities when Te=20 eV.

2.3 等离子体辐射不透明度模型

等离子体不透明度表征等离子体以及辐射场之间的能量交换.其中普朗克不透明度表征光学薄条件下不同频率的光的辐射传输特性,罗斯兰不透明度表征光学厚条件下不同频率的光的辐射传输特性.不透明度由THERMOS 程序[30]计算,计算过程如下: 1)首先采用修正的FAC (flexible atomic code)[31]计算原子能级结构和振子强度,FAC 中原子结构的计算基于相对论组态和各个独立粒子的基本波函数的相互作用,这些基本波函数是由一个中心势模型推导,通过引入Dirac-Coulomb 哈密顿量充分引入相对论效应[32];2)按照2.2 节中碰撞辐射模型计算得到的锡组态分布,将锡等离子体的吸收谱叠加平均,最后得到普朗克以及罗斯兰不透明度[33].本文将不透明度按照光子频率划分24 个群,并为辐射波长在13—14 nm的光子单独设置一个群,便于追踪EUV 辐射的时空分布.

3 模拟结果

本节采用Z* code 对激光诱导固体锡靶放电实验[34]进行模拟,模拟条件和实验条件一致: 放电电压–7.2 kV,放电电容0.25 μF,电感2.6 μH.电流波形如图4 所示.

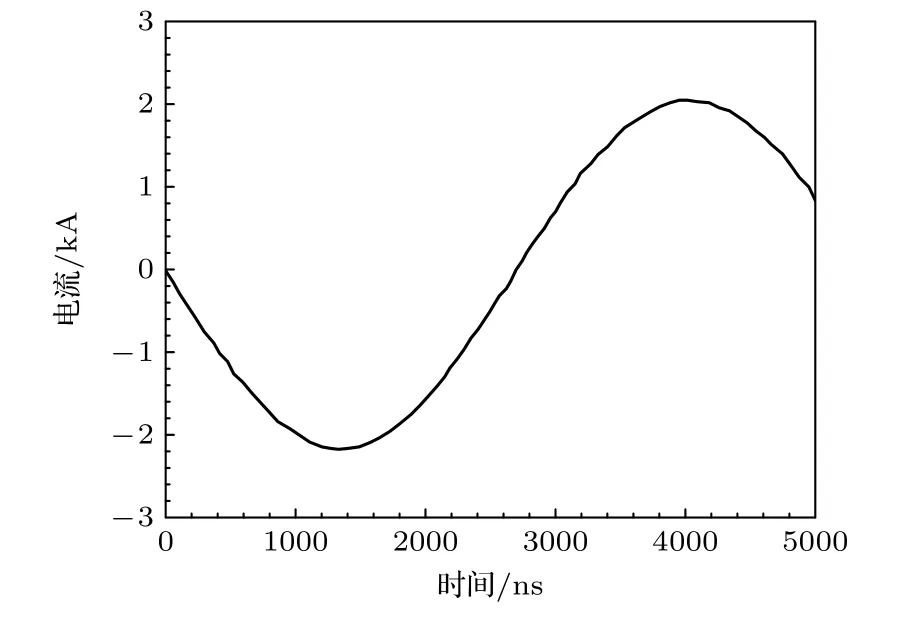
图4 激光诱导放电模拟过程中电流波形Fig.4.Simulation of current waveform during laser induced discharge.

阳极为直径1 cm、厚度3 mm 的固体锡靶,阴极为半径5 mm 不锈钢球形电极,电极间距为7 mm.脉冲能量120 mJ、脉宽90 ns 的CO2激光由阴极中心处垂直入射聚焦于锡靶,焦斑半径为300 μm,功率密度沿径向呈高斯分布.LDP 等离子体密度分布如图5 所示,电流上升初期,等离子体主要集中在阳极附近,如图5(a),(b)所示.随着电流的上升,等离子向阴极扩散,见图5(c),(d).本文将阳极等离子体前沿膨胀到阴极的时刻定义为电弧的形成时刻,1200 ns 时刻电弧形成并且沿径向扩散,如图5(e),(f)所示.在1840 ns 即电流峰值时刻电弧开始收缩,见图5(g),(h),2400 ns后电弧重新开始膨胀.

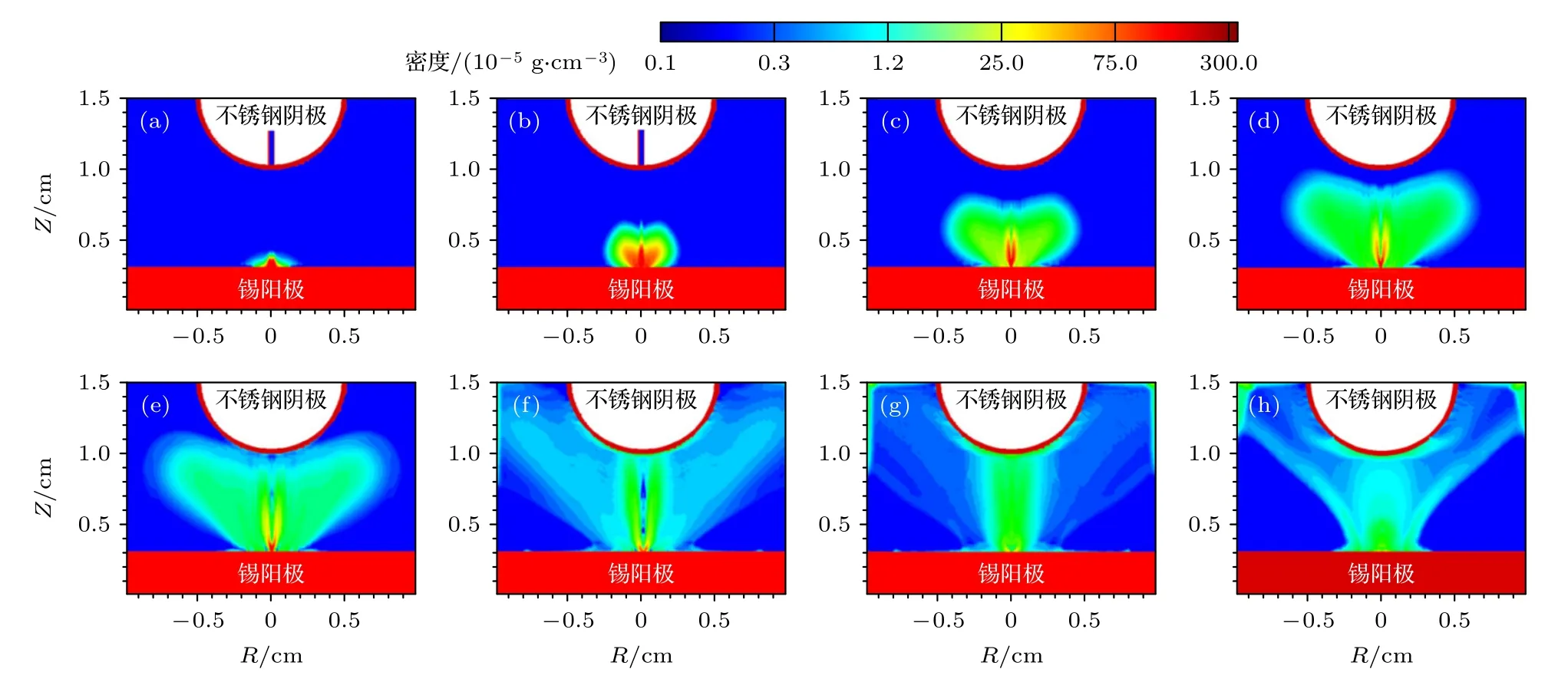
图5 放电过程中等离子密度模拟 (a) 320 ns;(b) 480 ns;(c) 720 ns;(d) 960 ns;(e) 1200 ns;(f) 1840 ns;(g) 2400 ns;(h) 2700 nsFig.5.Simulation of plasma density during discharge: (a) 320 ns;(b) 480 ns;(c) 720 ns;(d) 960 ns;(e) 1200 ns;(f) 1840 ns;(g) 2400 ns;(h) 2700 ns.

EUV 辐射分布如图6 所示.在电流上升初期,EUV 辐射主要集中在阴极附近,随着电流的上升,EUV 辐射功率增强,垂直于放电轴方向出现EUV辐射.当电流达到峰值时,垂直于放电轴方向EUV 辐射消散,EUV 辐射在主要集中在两个电极附近.当电流下降时,EUV 辐射在主要集中阳极附近,强度逐渐减弱.

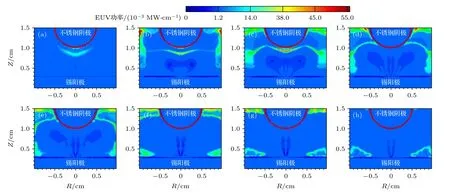
图6 放电过程中极紫外辐射功率密度模拟 (a) 480 ns;(b) 704 ns;(c) 382 ns;(d) 1008 ns;(e) 1152 ns;(f) 1328 ns;(g) 1504 ns;(h) 1712 nsFig.6.Simulation of EUV radiation power during discharge: (a) 480 ns;(b) 704 ns;(c) 382 ns;(d) 1008 ns;(e) 1152 ns;(f) 1328 ns;(g) 1504 ns;(h) 1712 ns.

4 讨论分析

将模拟的放电等离子演变过程(图5)和实验拍摄的等离子体可见光羽辉图像(图7)[34]进行对比,发现实验和模拟结果得到的等离子体发展规律基本一致.在第1 个电流半周期(0—2750 ns)中,激光诱导放电等离子体经历了等离子体由阴极向阳极扩散、电弧形成、电弧扩散、电弧收缩以及电弧再次扩散这5 个阶段.

图7 放电等离子体羽辉图像[34] (a) 300 ns;(b) 450 ns;(c) 600 ns;(d) 750 ns;(e) 900 ns;(f) 1050 ns;(g) 1200 ns;(h) 1350 ns;(i) 1500 nsFig.7.Discharge plasma plume images[34]: (a) 300 ns;(b) 450 ns;(c) 600 ns;(d) 750 ns;(e) 900 ns;(f) 1050 ns;(g) 1200 ns;(h) 1350 ns;(i) 1500 ns.

将4π 立体角内辐射功率密度积分,可得到辐射总功率以及EUV 辐射功率随时间变化.如图8所示,结合电流波形发现两点规律: 1)尽管两个半周期电流强度相差不大,但是第1 个电流半周期(0—2750 ns)内EUV 辐射强度远高于第2 个电流半周期(2750—5500 ns),这是由于第1 个电流半周期结束后等离子体还处于膨胀状态,导致第2 个电流半周期内等离子体未能形成有效箍缩,整体等离子体尺寸太大,EUV 的辐射损耗高[35];2)光辐射总功率和EUV 辐射功率出现峰值的时刻并不重合: 辐射总功率峰值出现在电流达到峰值后,而EUV 辐射功率的峰值出现在电流上升期间,这与之前的实验结论吻合[34].在传统的Z 箍缩研究中,等离子体箍缩到心时辐射总功率最强,这一现象与本文一致.电流达到峰值后由于电弧仍然处于收缩阶段,电流密度并未立刻下降,因此辐射总功率峰值相对电流峰值有滞后.EUV 辐射不仅与等离子体温度也和等离子体密度相关,EUV 辐射峰值对应着电流上升阶段,此时电流变化率较大,径向磁压力使得等离子体发生箍缩[15],提高了EUV 辐射区的温度和密度.总体看来,辐射总功率主要受电流密度影响,而EUV 辐射功率受电流密度上升速率的影响.

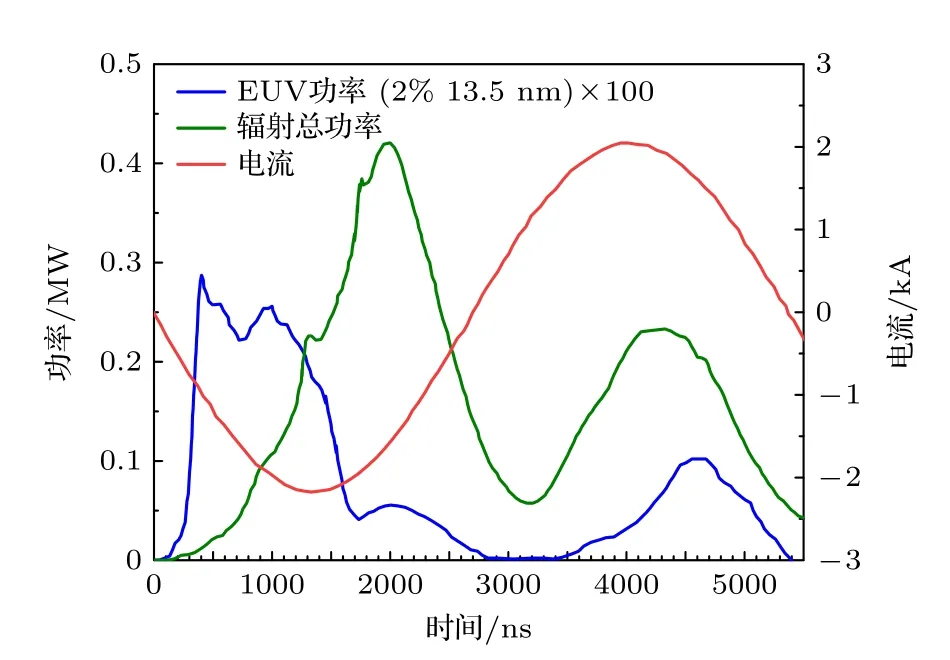
图8 放电过程中光辐射总功率及极紫外辐射功率时域波形Fig.8.Waveforms of total optical radiation power and EUV power during discharge.

对EUV 转化效率(η)和光谱纯度(SP)进行估算,如(25)式和(26)式,这里PEUV是13.5 nm 附近2%带宽内EUV 辐射功率,Pall是全波段光辐射功率,积分时间选取第一个电流周期,C和U分别是放电储能电容和电压.计算得到储能电容总能量6.48 J,总辐射光能量842 mJ,2%带宽内EUV辐射能量3.5 mJ,EUV 转化效率约为0.054%,EUV 光谱纯度为0.42%:

该EUV 转化效率与之前实验[36]估算的结果相差不大,但相比其他机构的研究成果[11],本文转化效率和光谱纯度相对较低,主要原因是电流的上升速率小,箍缩不充分,电极间辐射区的温度和密度较低,低价锡离子仍然占主导.同时等离子体尺寸较大,一部分EUV 被外围的低温等离子体区重吸收.

5 结论

本文基于全局EOS 模型、碰撞辐射模型和相对论的原子结构程序,提出了一个磁流体辐射模型,对激光诱导放电等离子体动力学过程及EUV辐射特性进行了模拟,模拟发现电流上升阶段等离子体的箍缩效应与EUV 产生有着密切关系.该模型和实验结果一致性较高,对国内LDP 动力学研究进行了有效补充,该模型适用于后续激光参数、电流波形、电极间距等对 EUV 辐射特性影响的分析,为掩膜检测的LDP-EUV 光源的研发提供了初步的参考.因此在未来的工作中将进一步研究提高LDP-EUV 的转化效率.