统计学教学中有关方差分析问题的探讨

张 侠，杨冰清，王海亭

（阜阳师范大学 信息工程学院，安徽 阜阳 236037）

方差分析是常用的统计方法，已被应用到各学科各领域当中。方差分析是统计学和概率论与数理统计中非常重要的章节。在科学研究与生产实践中，一个事物常常受许多错综复杂的因素影响[1]。方差分析主要通过数据分析探究对该事物显著影响的因素及其交互作用，或影响因素的最佳状态。变量间关系可以分为函数关系和相关关系，函数关系是多对一或一对一的映射，如产品销售额与销售量的关系。相关关系是一对多的映射，如子女身高与父母身高间的关系。函数关系和相关关系可以相互转化，函数关系是相关关系的特例。当两个变量有相关关系，并不代表有因果关系，判断两个变量是否具备因果关系的统计方法主要有两种：参数统计法，如检验和方差分析；非参数统计法，如Kruskal-Wallis 分析和Friedman 分析[2-3]。实际问题中，往往需要判断一个变量对另一个变量是否具有因果关系。这就需要方差分析来解决。

本文主要围绕“提出问题，分析问题和解决问题”的思路展开分析。首先，探讨方差分析概念、解释其基本思想、分析其优势，探寻方差分析和回归分析的关系；其次，详细解释方差分析计算步骤和求解方法。最后，强调掌握统计思想和统计方法的应用，引用两个案例，详尽探究方差分析的实践应用过程。

1 方差分析的基本问题

1.1 概念及基本思想

方差分析在经济学、社会学、医学、商业和农业等诸多领域的数量分析中，发挥着极其重要的作用。方差分析是推断统计中一种非常重要的统计方法，它表面上是检验多个总体的均值是否相等，其本质是检验分类型自变量对数值型因变量的影响[4-5]。如检验行业对被投诉次数是否有显著影响，检验颜色对商品销售量是否有显著性影响等。依据分类型自变量的个数，将方差分析分为单因素方差分析和双因素方差分析。本文仅探讨单因素方差分析。其基本思想：自变量对因变量没有显著影响，组间均方等于组内均方；反之，组间均方远大于组内均方[6]。

1.2 方差分析的优势与不足

方差分析的优势：方差分析是假设检验的延续。相较于t检验，在检验多个总体均值相等与否时，方差分析不仅能提高检验的效率，还将所有样本信息融合在一起，减少犯α错误的概率，排除了错误累积的概率，增加了分析的可靠性[7-8]。

当然，方差分析有其不足之处：当检验结果拒绝原假设时，表明总体均值不全相等，方差分析不能得出均值大小的结论[9]。

1.3 方差分析与回归分析的关系

现有文献对于方差分析和回归分析二者关系少有深入分析，回归分析使用到方差分析思想，体现在方差分解上，总方差分解为回归方差与残差方差。正如参数显著性检验是方程显著性检验的特例，方差分析是回归分析的特例。二者既有区别又有内在联系，详见表1 所示。

表1 方差分析与回归分析的关系

2 方差分析的基本方法

2.1 直观描述

如何判断自变量对因变量是否有显著影响？画出因变量与各因素的箱线图，使用中位数线将各因素对应的因变量中位数联系起来。通过箱线图进行直观判断[10-11]。

2.2 方差分解

本文仅考察单因素方差分析，即一个自变量对一个因变量的影响。X表示自变量，Y表示因变量。检验X在不同水平的变动对Y是否有显著影响。单因素方差分析数据结构见表2 所示。

表2 单因素方差分析数据结构

xi(i=1,2,3,…,k)代表水平，分别来自于k个不同总体，yij表示第i个水平第j个观测值。从不同总体中抽取样本分别为n1,n2,…,nk[12]。

方差分析的基本步骤包含提出假设、构造统计量F和依据决策规则作出统计决策。下面分别进行详细具体的分析：

2.2.1 提出假设

假设是对一个问题的看法，分为原假设和备择假设。方差分析首先提出原假设H0:μ1=μ2=…μk，表示自变量对因变量无显著影响；备择假设H1:μ1,μ2,…,μk不全相等，表示自变量对因变量有显著影响。

2.2.2 构造统计量F

2.2.3 作出统计决策

为检验自变量X对因变量Y是否有显著影响。比较统计量与临界值Fα(k-1,n-k) 大小即可，若F≥Fα(k-1,n-k)，拒绝原假设，表明总体均值有显著差异，说明自变量对因变量有显著影响。若F＜Fα(k-1,n-k)，没有充分理由拒绝原假设，表明总体均值没有显著差异，说明自变量对因变量没有显著影响。方差分析的一般形式，详见表3。

表3 方差分析一般形式

3 方差分析应用案例

前面详细探讨了方差分析的概念、基本思想和求解步骤，为深入理解方差分析在实践当中的应用，接下来通过两个实践案例分别梳理方差分析的详细求解过程。

案例1：某高校财务管理、国际商务和中韩财管等3 个专业学生统计学笔试考试分数（原始数据略），试分析专业对统计学分数有无显著影响。

各专业统计学分数描述统计分析如表4 所示。

表4 统计学成绩描述统计分析

3.1 直观分析

这是一个探讨分类型自变量（专业）对数值型因变量（统计学分数）的影响，方差分析正是解决这一类问题的。首先直观分析，详见箱线图1 所示。

图1 不同专业统计学成绩的箱线图

从图1 可以看出，不同专业的统计学成绩具有显著差异，即便同一专业，不同学生统计学分数也明显不同。具体来看，财务管理专业中位数较高（80），中韩财务管理专业中位数较低（64），箱线图呈现的是专业与统计学分数之间有一定关系，否则的话，中位数应该大致相同。

直观分析不能充分证明不同专业的统计学分数有显著差异，需要进一步借助精确的方法即方差分析来解释，下面进行方差分解的赘述。

3.2 方差分解

接下来按照上面三个步骤提出假设、构建统计量、作出统计决策来进行方差分解：

第一，提出假设。

原假设H0:μ1，μ2，μ3，即专业对统计学分数无显著影响；备择假设H1:μ，μ2，μ3不全相等，即专业对统计学分数有显著影响。

第二，构建统计量。

组间方差、组内方差分别除以各自对应的自由度，即得组间均方

和组内均方

最后，构建统计量

查F分布表F0.05(2,73)=3.1 221。

第三，作出统计决策。

由统计量F=14.7 612，查分布表，临界值F0.05(2,73)=3.1 221，即F＞F0.05(2,73)，因此拒绝原假设H0，说明均值不全相等，说明专业对统计学分数有显著影响，这和事实吻合，究其原因：统计学学科的学习要以高等数学为基础[13-15]。

综上，方差分析表如表5 所示。

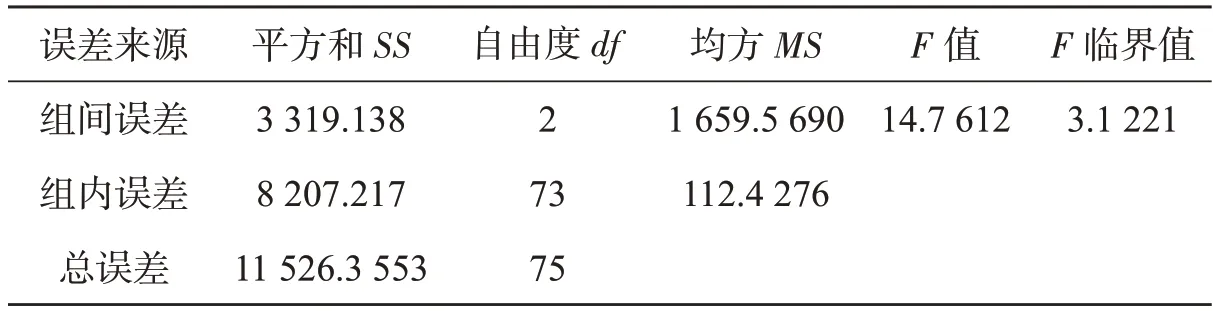
表5 方差分析表

软件实现：打开方式使用office打开，依次点击文件、选项、加载项、数据分析工具库、确定。在菜单栏中点击数据分析，选定输入区域和输出区域后确定，即出现方差分析列表,如图2 所示。其优势是实现数据个数多、数据复杂、手工计算相对困难的情况使用软件实现，可以提升计算的效率和准确性。

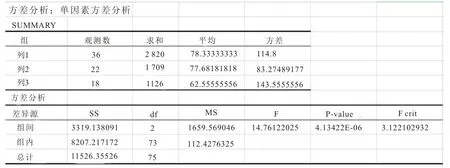
图2 EXCEL 方差分析的输出结果

案例2：凯恩斯消费理论：随着收入的增加，人们的消费支出会增加。那么，收入与消费之间具体数量关系是怎样的？试考察安徽2000-2016 年城镇居民人均消费y随城镇居民人均可支配收入x的变动规律[16]。

要判断城镇居民人均消费y随城镇居民人均可支配收入x的变动规律，回归分析可以解决，在进行回归分析之前，首先绘制散点图，通过散点图进行直观判断，如图3 所示，直观判断二者大致呈现线性关系[17-18]。

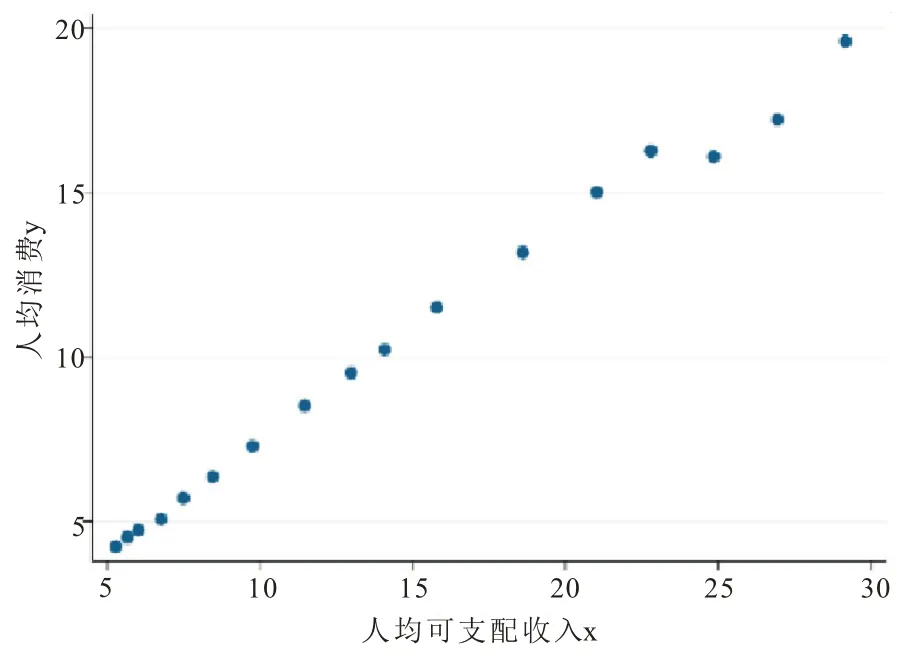
图3 人均消费y 与人均可支配收入x 关系的散点图

则估计的回归方程为：

回归模型未必可靠，需要进一步进行检验，其中在回归分析模型的检验中，需要进行方程整体显著性检验，借用了方差分析的思想，因此，国内教材多把方差分析安排在回归分析之前[19-21]。回归分析中借用方差分析的思路为，总方差分解为回归方差（x解释的部分）与残差方差（x未解释的部分），为检验x对y是否有线性影响，构造如下检验统计量。F=～F(1,n-2)，SSR为回归方差，1 为自由度，SSE为残差方差，n-2为自由度。可以用F检验的理论来检验线性模型是否成立。

计算回归方差SSR=411 168 034.8 233，残差方差SSE=2 921 237.5 182，回归均方

计算统计量

常用置信水平下，F0.05(1,15)=4.5 430 。F＞F0.05(1,15)，拒绝不存在线性关系的原假设，表明人均可支配收入对人均消费存在线性影响，模型通过方程的显著性检验，即模型通过线性关系检验，说明回归模型能合理解释实际问题。

人均消费y随城镇居民人均可支配收入x的变动规律是：人均可支配收入每增加1 元，人均消费支出平均增加0.6 351 元。这符合凯恩斯消费理论，并且与经济事实相符。

4 结语

本文探讨统计学教学中方差分析相关问题，阐释了方差分析的概念、基本思想和分析方法，并详细给出其求解步骤，深入解析方差分析与回归分析的关系，为更好地对方差分析有个深刻的理解，学以致用，真正掌握和应用方差分析解决现实问题。本文通过两个案例进行一一具体分析，并将方差分析和回归分析结合起来，为熟练掌握和应用方差分析打下坚实基础。