高职涉农专业学生实习调研分析及评分权重优化研究

刘 冬

（安庆职业技术学院，安徽安庆 246003）

实习是高职涉农专业人才培养方案的重要组成部分，对培养学生良好的职业道德、熟练的专业技能和可持续的自学能力等具有重要的意义［1］.但实习往往存在各种各样的问题，实习指导与监管不到位，实习质量监控难和考核评价不完善等问题已成为研究人员关注的焦点，尤其是考核评价方面［2-3］.实习考核一般从实习态度、实习成效和服从纪律情况等方面入手，高职院校对学生实习成绩的评分组成较为相似，但考核指标权重存在较大差异［4-5］.

为合理地评价学生实习得分，真实地反馈实习的教学效果，我们整理了安庆职业技术学院园林园艺系往届涉农专业的实习材料，并设计了实习质量、满意度和企业反馈问卷.2018 年11 月-2022 年11 月共发放调查问卷1 000 份，回收有效问卷982 份.问卷调查结果显示95.3%的受调查者支持实习学生自评得分、校内指导教师和校外指导教师评分三者之间应比较接近才能较好地反映学生顶岗实习的质量.其中90.6%受调查者支持三者之间的接近程度可作为各指标权重优化的目标，而三者间的相对标准偏差，是反映其接近程度的有效方法［6］.教育学家布鲁姆的形成性评价支持实习评价的过程化和多元化，包括学生自我认知和教师对学生的评价.形成性评价在实习教学环节更加契合，能及时提供反馈信息，帮助调整实习教学策略，优化实习管理［7］.由于各高职院校在评分权重方面存在较大差异，且各专业人才培养的侧重点也有所不同，因此根据涉农专业自身特点和人才培养目标优化评分权重，有效的反馈实习效果是十分必要［8］.本研究旨在调研结果的基础上以学生自评得分、校内和校外教师评分三者之间的相对标准偏差最小为优化目的，达成形成性评价目标.

笔者利用中心组合试验优化各指标权重比例，为涉农专业学生实习效果的合理评价提供理论基础.

1 研究对象与方法

1.1 研究对象

以安庆职业技术学院近5届涉农专业1 000名实习学生为研究对象.

1.2 研究方法

1.2.1评分权重的优化

在前期982份问卷调查结果的基础上，选择校外指导老师评价所占评分权重、校内指导教师评价所占评分权重、学生实习日志和实习总结等材料所占评分权重，顶岗实习座谈交流所占评分权重为优化对象.用Design expert 6设计的四因素中心组合试验组合表（表1）进行问卷调研.30名同学的调查结果为一组，取平均值，共29组.以学生自评得分和校内校外教师评分的接近程度为优化指标，把数据按照公式（1）处理获得相对标准偏差（RSD），以其最小为优化目标，求平均值（公式2），借助中心组合试验优化评分权重.以112名同学的调查结果为样本，进一步验证优化模型的准确性.

表1 中心组合试验设计与试验结果

y为实习学生的得分，n=4分别为实习相关材料、学生自评分、实习单位指导评分和学校指导教师评分（1）.

1.2.2数据分析

以excel 按照公式（1）和（2）计算相对标准偏差和平均相对标准偏差（------RSD），用Design expert 6处理中心组合试验结果，绘制单因素和响应曲面图.

2 结果与分析

2.1 学生关心的实习问题分析

座谈和调查结果显示，学生关心的实习问题如图1 所示包括实习工资、希望缴纳五险一金、工作时长、是否需要加班、工作内容、吃住安排和签订合同等.从这些关心的词语和座谈会反馈显示学生希望实习期间能签订合同保护自身合法收益、获得合适的薪资待遇、实习单位缴纳五险一金和实习单位有统一的后勤保障等.

图1 学生关心的实习问题云词

2.2 实习单位特征分析

在涉农专业群学生实习的2018-2022年期间本地就业率不断增加，麦克思统计结果显示截止到2022年12月份安庆市本地就业率达到45%，如图2.涉农专业实习单位主要是民营企业和合资企业，占50%以上.实习单位规模较大，近80%的学生在企业规模≥180 人的单位实习，它们是省内涉农产业领域中的知名企业或龙头企业.实习单位对口率约为92%，实习就业一体所占比46%，52%的同学在实习期间获得轮岗机会，85%的同学对实习薪资满意.

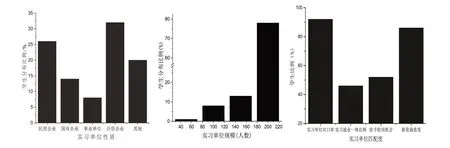
图2 实习单位特征

2.3 学生能力与实习岗位衔接情况分析

由图3可知62%和26%的同学认为本人能胜任实习岗位所需的专业知识和职业技能，2%的同学反馈未能很好地胜任实习岗位.80%以上的同学认为专业知识和职业技能对实习岗位任务的完成有较大的帮助；72%的同学认为素质拓展和劳动教学对完成实习任务有帮助，但素质拓展应用企业需求衔接度有待提高，而在校的劳动教育增加了其吃苦耐、劳爱岗就业的精神和健康强健的体魄；计算机、语文、英语和体育等基础知识对其实习和就业有一定的促进作用，41%的同学认为社团活动对其实习和就业有帮助.

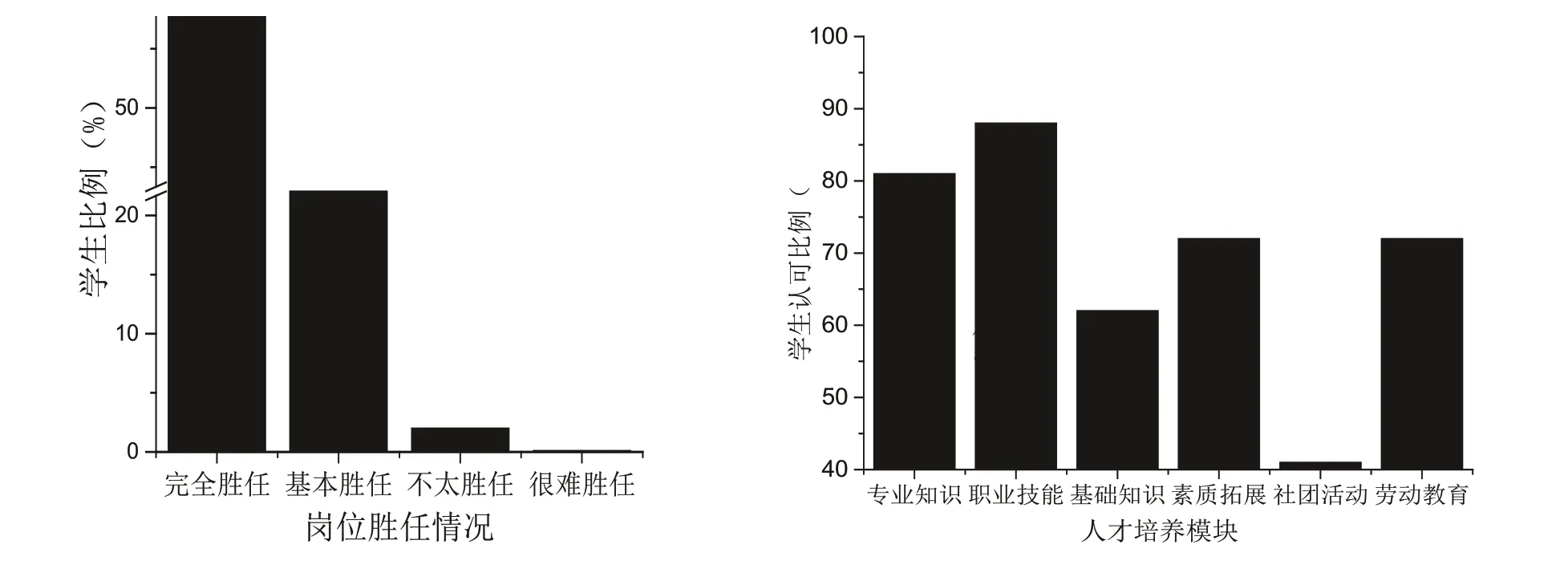
图3 学生能力与实习岗位衔接情况

2.4 实习管理提质及考核评价

实习管理提质工作从实习总体安排是否合理，实习收获情况、影响实习效果的主要因素和实习总体满意度等四方面评价.图4 显示84%的同学认为实习安排合理，实习6 个月能大幅度提高职业技能；16%的同学希望实习安排更灵活一些，可以出省实习，缩短实习时间保证专升本学习的需求；92%的学生认为实习收获颇丰，与预期一致或高于预期；66%、55%、86%和75%认为企业实习氛围、实习岗位有趣性、实习指导老师和自身专业知识与能力是影响实习效果的主要因素；而学校的管理相对薄弱仅22%的同学认为其对实习效果有影响；72%的同学对实习总体满意，20%认为实习情况良好较满意；3%的同学认为过多地强调本地实习和就业对同学们视野的开阔不利，如果没有优秀的企业较大面积地在本地就业会造成教学实习质量下滑.

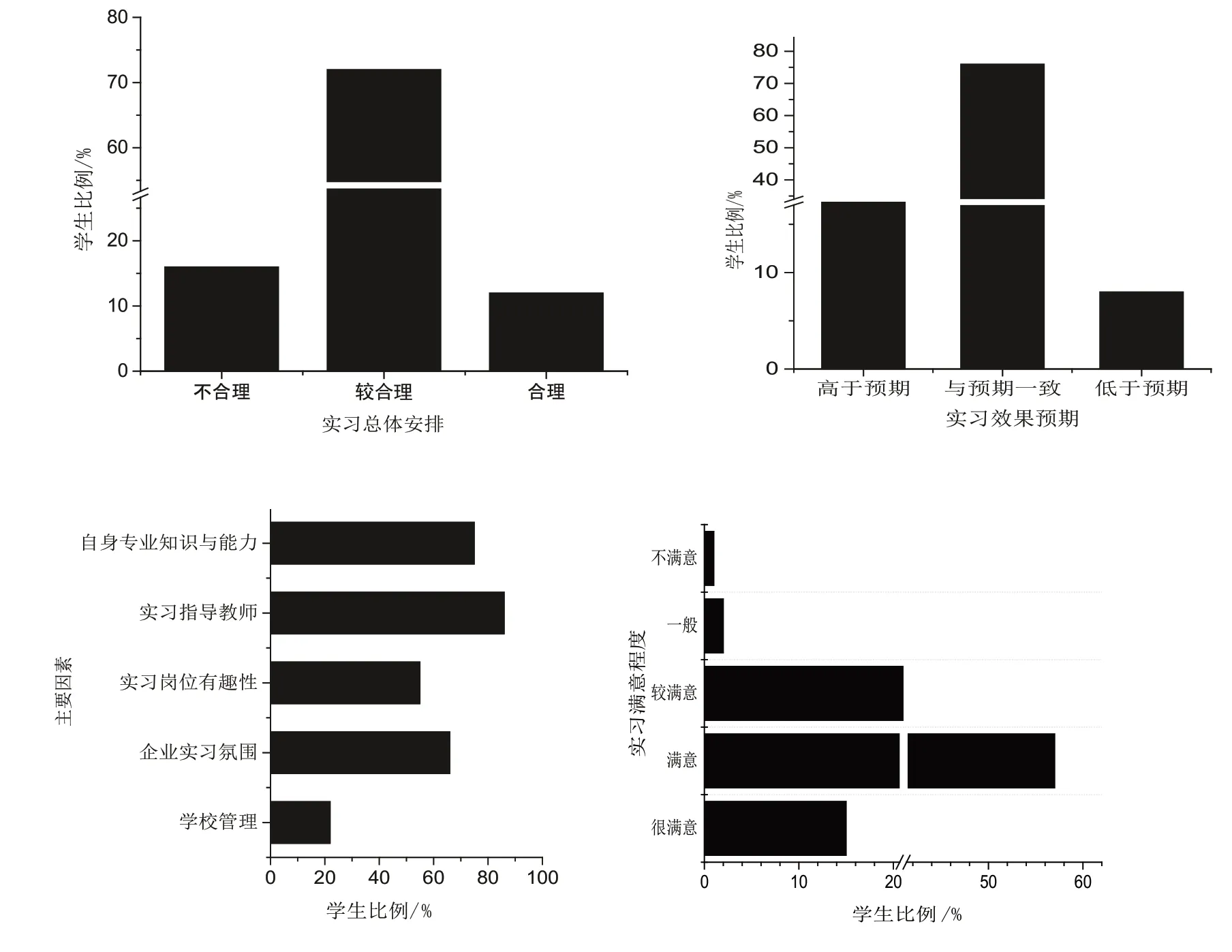
图4 实习管理提质影响因素

实习相关材料是指导教师评分的重要依据［2-4］，安庆职业技术学院利用习讯云APP进行过程管理实现打卡签到、实习申请变更、实习材料收集和交流互动平台，实现实习指导信息化、实习管理规范化、实习过程具象化、实习总结及时化.实习调研显示学生认同实习报告、实习日志和周记等是指导教师评分的重要指标，学校应增加座谈和实习展示环节，这样可以更好地提高实习质量.前期实习调研和座谈得出95.3%的学生支持实习学生自评得分、校内指导教师和校外指导教师评分三者之间应比较接近才能较好地反映学生实习的质量，90.6%的三方调查结果显示（企业、学校和学生）支持三者之间的接近程度可作为各指标权重优化的目标，支持可用其来检验实习的考核的准确性和科学的观点.

2.5 四因素中心组合试验优化考核权重

教育学家布鲁姆的形成性评价理论，结合前期实习调研和座谈中78.2%的受访者认为校外指导教师的评分权重应占20%-50%，校外教师评分所占权重（X1），75.3%的问卷支持校内教师评分权重应在10%-30%，校内教师评分所占权重（X2）.81.1%的参与者认为学生所提的实习材料得分权重（X3）应在10%-30%.实习座谈交流是考查学生实习效果的有效途径之一，指导教师可以根据座谈中学生表现了解学生的实习情况［4-5］，80.7%的问卷支持实习座谈交流自评结果权重（X4）在5%-20%较为合理.选择校外实习指导教师评分所占权重（X1）、校内教师评分所占权重（X2）、实习相关材料所占权重（X3）和学生自评所占权重（X4），按表1 进行调查，调查结果如表1所示.用Design expert 6进行分析，结果表明X2、X3和X4对RSD值有明显影响（P＜0.01，见表2）.另外，X1X2、X1X3和X2X3的交互项及四因素的平方项也对RSD 值有显著影响［9］.回归方程Y=4.06-0.46X1-2.91X2-1.98X3+3.21X4-5.22X1X2+2.8X1X3+1.55X1X4-3.52X2X3+0.78X2X4-0.95X3X4+3.67X12+5.27X22+6.17X32+1.8X42（3）.方差结果显示，方程（3）的P模型＜0.000 1、P失拟项=0.171 5＞0.05、R2=0.97、Adj R2=0.93、PredR2=0.82.结果表明方程（3）显著，无失拟因素存在，能较好地反应四因素与RSD 的关系［10］，并具有良好的重现性［10-11］.由方程（3）任选两因素为变量，另两个因素固定在中心点作图5（a-f），由图5 可知方程（3）存在最小值点，RSD 约为2.9%.此时X1、X2、X3和X4分别为38%、26%、26%和10%，在该条件以32份调查问卷的平均相对标准偏差值进行验证试验RSD=2.93%，预测值和试验结果一致.

表2 二次多项式模型回归系数估计和试验结果方差分析

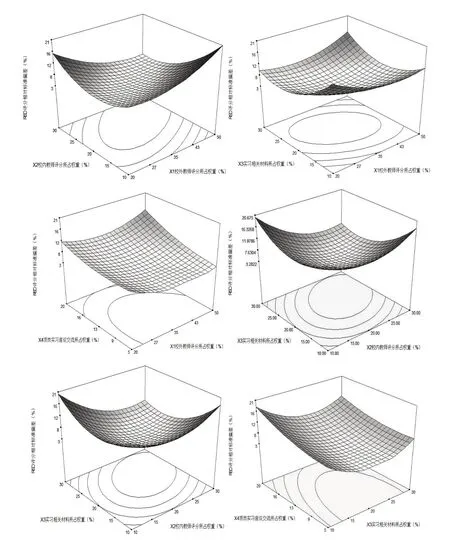
图5 四因素交互作用响应面

3 结论

通过982份调查问卷和座谈发现学生关心的实习问题包括薪资、工作时间和加班与否等.结果发现学生的专业知识和职业能力与实习岗位衔接情况良好，能满足实习需要.84%的同学认为实习安排合理；97%的同学对实习表示满意，但还有需要待改进工作如不应过多地强调本地实习和就业对同学们视野的开阔不利.在调研和访谈结果的基础上，以中心组合试验对校外教师、校内教师、实习相关材料及实习座谈交流所占的权重比例进行优化.结果表明当校外教师评分所占权重为38%、校内教师评分所占权重为26%、实习相关材料所占权重为26%、实习座谈交流所占权重为10%时，学生自评得分和校内外教师评分比较接近.