AlGaAs基光电阴极光学性质计算模型分析

赵 静,冯 琤,覃 翠,郭 婧

(1. 南京工程学院信息与通信工程学院, 江苏 南京 211167;2. 南京工程学院自动化学院, 江苏 南京 211167)

负电子亲和势AlGaAs/GaAs光电阴极量子效率高、暗电流小、长波响应好、电子出射的平均能量及角分布小、工作模式符合日常使用习惯,可广泛应用在微光像增强器、半导体敏感器件、自旋电子学、新一代加速器电子源等众多领域[1-5].自从GaAs光电阴极出现以来,主要研究集中于光电阴极带宽的拓展、积分灵敏度的提高、激活方法的优化、寿命问题的探索等[6-12].不同应用场景下对光电阴极光谱响应的要求不同,夜空辐射的光谱范围集中在500～1 700 nm,标准微光夜视用三代GaAs光电阴极通常注重于长波响应的拓展;在沙漠、水中、海域等特殊环境下,来自目标的图像信息响应范围为430～570 nm的蓝绿光波段,故用于沙漠、海水探测的AlGaAs光电阴极需要短波响应较高[13-14].通过结构设计,AlGaAs/GaAs光电阴极可从理论上满足不同场合不同光谱的需求,因此需要分析不同结构的光电阴极在不同光谱下的光学性质.这里的结构设计包含不同组分、掺杂的AlGaAs材料,可以统称为AlGaAs基光电阴极.

由光电发射模型可知,参与发射的光电子是来自于阴极吸收部分的光子,因此光电阴极的光学性能直接影响光电发射性能,吸收率的大小决定了光谱响应的高低.根据AlGaAs基光电阴极光学结构的通用性分析,本文拟建立适用于各类多膜层系光电阴极的光学性质计算模型,并经试验验证其有效性.基于模型研究光电阴极中发射层、窗口层、增透层厚度对单波长光子吸收的影响,研究400～900 nm不同波长响应时光电阴极的优化结构设计.

1 理论建模

构建一个适用于各类光谱响应的AlGaAs基光电阴极结构模型,包含玻璃基底、增透层、窗口层、若干发射层的多层膜结构,如图1所示.增透层通常采用Si3N4材料,厚度薄,在0.1 μm左右,主要用于增强光子入射率;窗口层是为了提升增透层和发射层间的晶格适配性而设置的一个缓冲结构,可采用与发射层材料类似的薄层;发射层是由不同组分或掺杂的Ⅲ-Ⅴ族半导体材料组成,组分与掺杂情况会影响光谱响应的范围;玻璃层比其他几个薄膜层厚很多,在光路结构中可以将玻璃看作光子进入光电阴极的入射介质,随后光电子依次通过其他三个薄膜层,从内部真空环境中射出,最后进入微通道板等部件进一步增强光电子.因此,从结构上来说,每个薄膜层结构参数对光电阴极的光学性质都有重要影响.根据薄膜光学矩阵理论,3个薄膜层可以分别用3个包含各层光学信息的特征矩阵来表示,通过矩阵计算可得到光谱吸收率.

图1 AlGaAs基光电阴极结构

计算多层薄膜结构的AlGaAs基光电阴极的光学性能时,为了与试验测试方式一致,反射率和透射率的光路顺序相反,矩阵计算分别进行.计算反射率时,从玻璃入射,矩阵计算顺序为增透层→窗口层→发射层1→发射层2→…→发射层K→空气,即:

(1)

需要注意的是,由于MZ、MC的形式与Mj一致,在后续计算中将它们合写在一起.

在计算透射率时,根据试验方法,光路方向为从空气入射到发射层,矩阵计算顺序为发射层K→…→发射层2→发射层1→窗口层→增透层→玻璃,即:

(2)

式中:Mg为玻璃基底信息;ηg为膜系出射介质玻璃的折射率.

MZ和MC的处理与反射率计算同理.这样,AlGaAs基光电阴极膜系组合的理论反射率Rthe、理论透射率Tthe和理论吸收率Athe的计算公式为[15]:

(3)

(4)

Athe=1-Rthe-Tthe

(5)

2 试验研究

为了验证模型设计的合理性,利用模型公式分别计算宽光谱响应和窄带响应两类光电阴极,并与试验曲线进行对比.试验样品A为一个梯度掺杂的GaAs光电阴极样品,窗口层Al组分为0.63,厚度为1 μm,发射层厚度为2 μm;试验样品B为一个对532 nm敏感的AlGaAs光电阴极,窗口层Al组分为0.79,厚度为0.5 μm,发射层Al组分为0.63,厚度为1.6 μm.样品A发射层按照等厚度梯度掺杂分布,样品B发射层按照递增厚度、递减掺杂分布,具体样品结构如图2所示,图2中仅给出窗口层和发射层结构,因增透层和玻璃基底相同,这里未画出.

(a) GaAs光电阴极样品A

图3分别为两种样品光学性质的理论计算结果和试验曲线.由图3可见,吸收区样品A、B的理论曲线和试验曲线反射率和透射率都出现了类似于干涉条纹的、峰谷相间的多层膜干涉效应,理论曲线与试验曲线形式上都非常接近.说明本文所建计算模型对于GaAs光电阴极和AlGaAs光电阴极有效,可应用于各类多层薄膜结构的光电阴极.理论与试验的主要误差来源于样品在制备过程中的实际厚度与设计厚度值之间有偏差,影响了理论计算结果,但这是可接受的,后期可通过厚度拟合来进一步缩减误差.图3(b)中,AlGaAs光电阴极的曲线误差稍大,原因是Al组分为0.79的AlGaAs材料的光学常数有缺失,采用了Al0.804Ga0.196As的光学常数值取代计算而造成的.

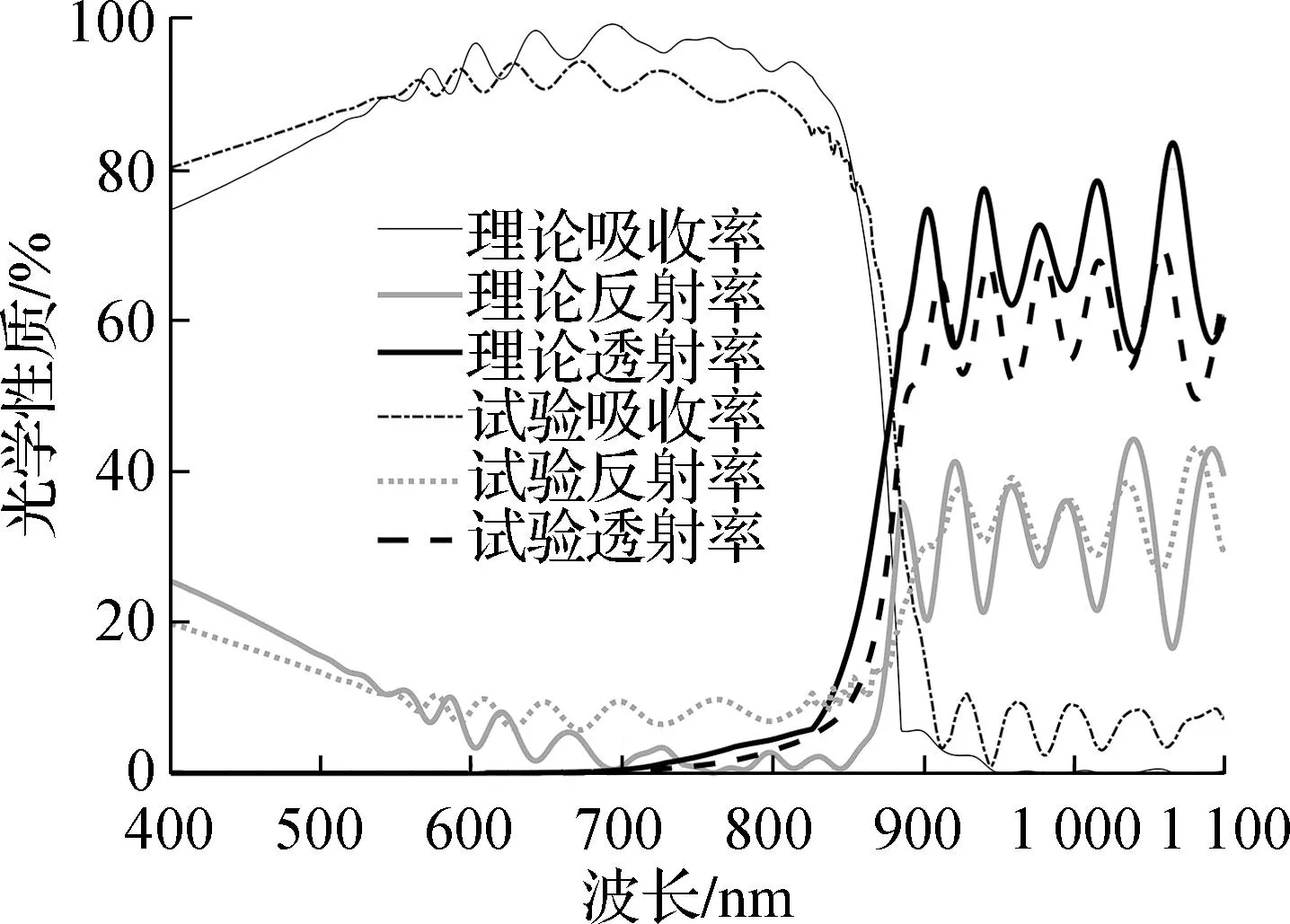
(a) 阴极样品A

3 仿真分析

AlGaAs基光电阴极包括若干AlGaAs发射层、AlGaAs’窗口层、Si3N4增透层、玻璃基底.为了研究除玻璃外各层对光电阴极性能的影响,本文仿真测试各层结构变化时各单波长点的光学性能变化情况.根据仿真结果,能分析出不同波长响应要求下应具有的阴极结构.

3.1 发射层厚度

首先讨论发射层的厚度对单点吸收率的影响关系,假设:只有一个GaAs材料发射层,发射层可以是均匀掺杂的、同一组分的单层结构,也可以是不同掺杂、同一组分的变掺杂结构,暂不考虑掺杂对光学性质的影响;AlGaAs’窗口层厚度为1 μm,Al组分为0.63,Si3N4增透层厚度为0.1 μm,GaAs发射层厚度在0～2 μm间隔0.1 μm变化.运用式(1)至式(5)分别计算波长在400～900 nm之间每间隔50 nm取值时的吸收率分布情况,如图4所示.由图4可见,吸收率随发射层厚度的增加而增加;从单波长响应来看,波长在400～500 nm时,吸收率几乎不受GaAs层厚度的影响,只随波长增加,这是因为GaAs层主要吸收长波光子,而短波光子主要被AlGaAs层吸收.因此,GaAs层对短波段的吸收率影响很小,几乎可以忽略.

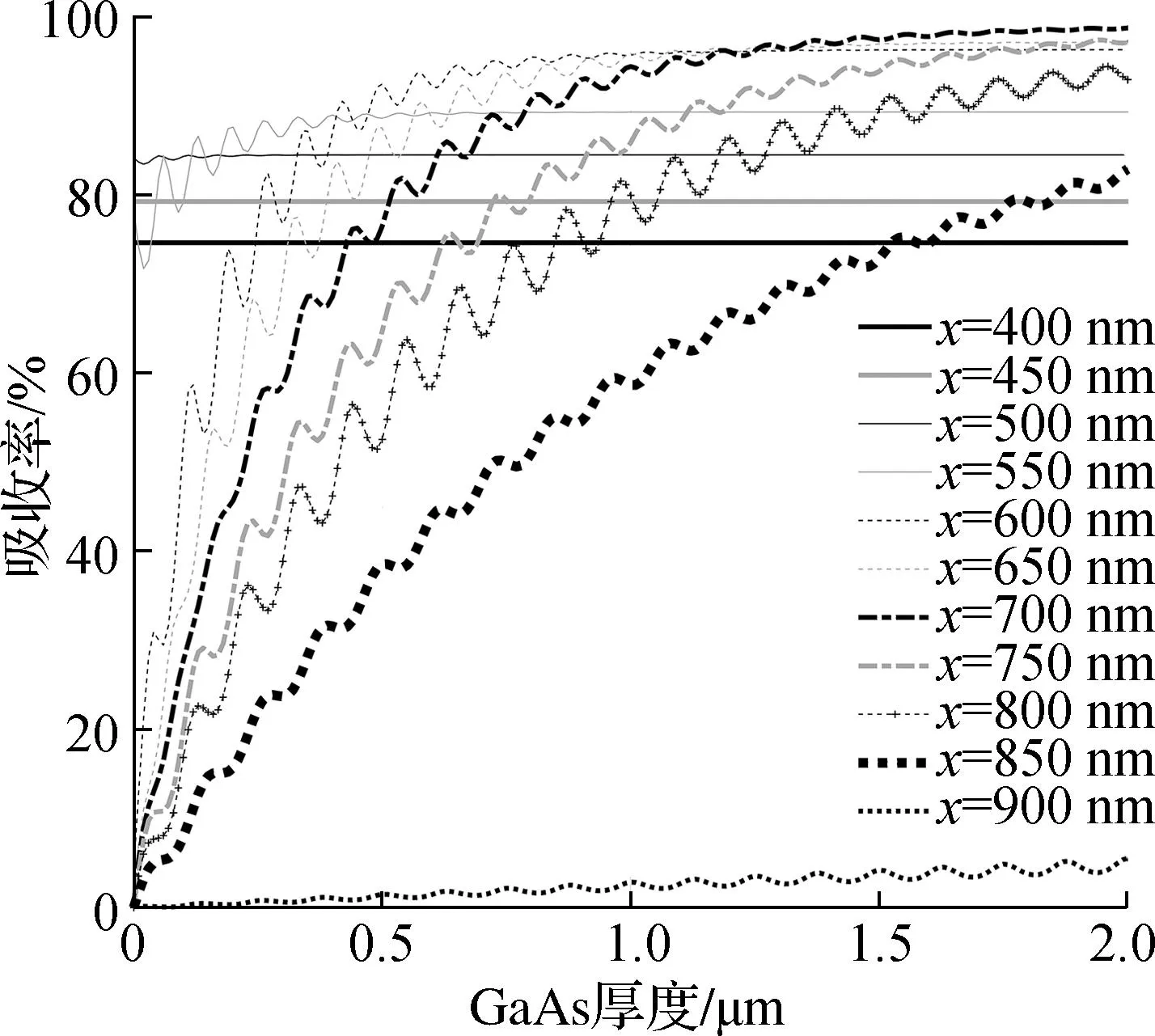
图4 吸收率随发射层厚度变化的分布情况

随着波长的增加,吸收率曲线先增大后减小,即存在一个最大吸收峰值.不同GaAs层厚度的峰值吸收波长不同,如表1所示.由表1中可见,发射层厚度越薄,峰值波长越小.这是由于长波光子吸收长度比较长,在更深的厚度处才被吸收.在半导体材料的吸收中,GaAs层厚度越薄,光子的波长越长,吸收能力越弱.因此,薄发射层的吸收率随波长的增加而降低,相反,发射层越厚,吸收的长波光子越多,较厚发射层的吸收率随波长的增加而增大.当厚度超过一定值时,光子被完全吸收,吸收率增加不明显.在800 nm以上,无论发射层的厚度如何,吸收率都随着波长的增加而降低.特别是900 nm后,吸收率几乎下降到0,即达到了GaAs材料的吸收极限.厚度为1.5 μm的发射层对应550～800 nm波段的光子绝大部分都能吸收,吸收率均超过90%,超过1.5 μm后吸收率随厚度的增加不明显.

表1 不同峰值吸收响应对应的GaAs发射层厚度范围

由表1可见,越长的波长响应对应的GaAs层厚度越厚,说明短波光子吸收长度比较短、在半导体表面吸收,长波光子吸收长度长、在半导体材料体内吸收.类似地,可以根据不同的吸收率要求,计算出不同波长响应对GaAs层结构的要求.当发射层厚度过低时,长波光子在发射层内吸收不充分,会影响长波量子效率;而发射层较薄有利于短波光子产生的光电子在被复合之前输运到表面,能有效提升短波响应.

为了进一步分析各波长光子在发射层内具体的吸收位置,将2 μm的发射层分割为10个子层,每个子层厚度为0.2 μm,计算若干波长点光子在10个子层内的吸收率,具体分布情况如图5所示.由图5可见,400～600 nm波段的光子主要在第一个子层被吸收,也就是发射层的表面0.2 μm内;700～800 nm波段的光子主要在前三个子层被吸收,也就是发射层的表面0.6 μm内;850 nm波段以后的光子在各子层间的吸收比较均匀,都在10%左右;900 nm之后已无吸收.

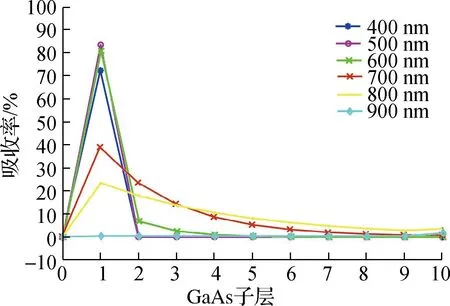
图5 GaAs各子层的吸收率分布情况

3.2 窗口层厚度

分析窗口层影响时,将发射层设计为单层情况,根据理论计算公式,假设GaAs发射层厚度为1.6 μm,Al组分为0.63,Si3N4增透层厚度为0.1 μm;AlGaAs’窗口层厚度在0～2 μm之间间隔0.1 μm变化,吸收率分布情况如图6所示.由图6可见:吸收率曲线受AlGaAs’层厚度的影响不大,只是部分波长处出现了峰谷现象,这是由于AlGaAs’材料的禁带宽度比较大,主要吸收短波光子,而短波光子大都在材料表面较浅的深度内被吸收,所以窗口层厚度的变化对吸收率的影响不明显;波长在400～700 nm时,不论窗口层厚度如何,吸收率都随波长的增加而增加,在700 nm时达到吸收峰值;波长在750～900 nm,吸收率随波长的增加而减小;波长在850 nm之后,吸收率急剧下降,减小到几乎为0;波长在550～800 nm.对于任意厚度的窗口层,吸收率都能达到90%以上.

图6 吸收率随窗口层厚度变化的分布情况

3.3 增透层厚度

假设AlGaAs’窗口层厚度为1 μm,Al组分为0.63,GaAs发射层厚度为1.6 μm,Si3N4增透层厚度在0～0.2 μm之间间隔0.01 μm变化,分别计算波长在400～900 nm之间每间隔50 nm取值时的光电阴极吸收率分布情况,如图7所示.由图7可见,AlGaAs基光电阴极组件吸收率的变化随增透层厚度不同出现了峰谷变化,变化周期约为0.1 μm.波长在400～700 nm,峰值大小随波长增大而逐步增加,峰值位置从0.04 μm变化到0.08 μm,0.046 μm的增透层在400 nm波长处达到吸收率峰值94.66%,0.076 μm的增透层在650 nm波长处达到吸收率峰值99.71%,这也是所有波长点的吸收率峰值;波长在700～900 nm,吸收率随波长增加逐步减小,波长在850 nm以后,吸收率减小得更为明显.

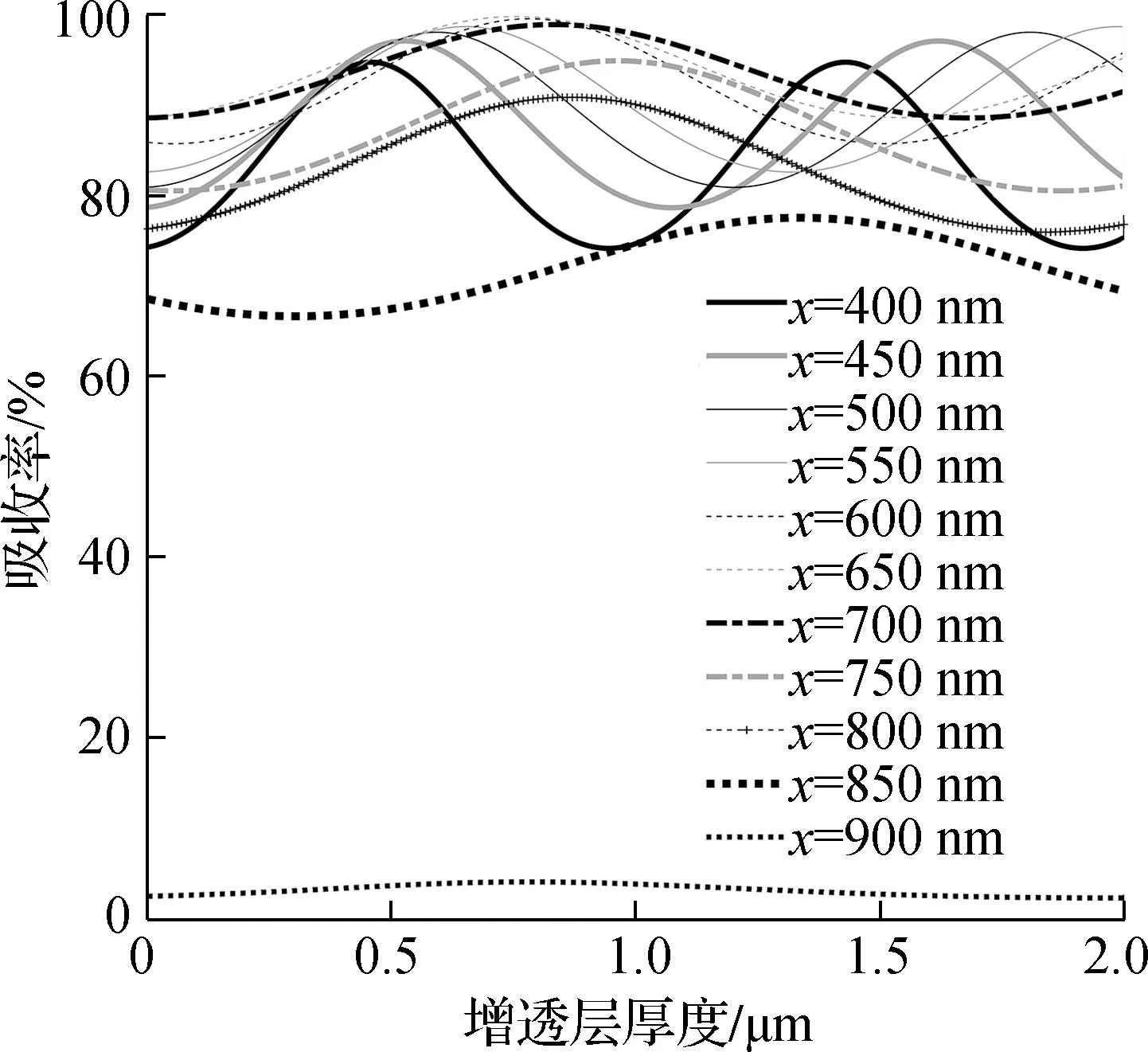
图7 吸收率随增透层厚度变化的分布情况

为了更细致地分析单波长处吸收率与增透层厚度间的关系,仿真计算吸收率峰值随厚度的分布情况,如表2所示.由表2可见,400～800 nm波段吸收率的峰值都超过了92%,其中400～550 nm波段光子峰值吸收率对应2个厚度值.

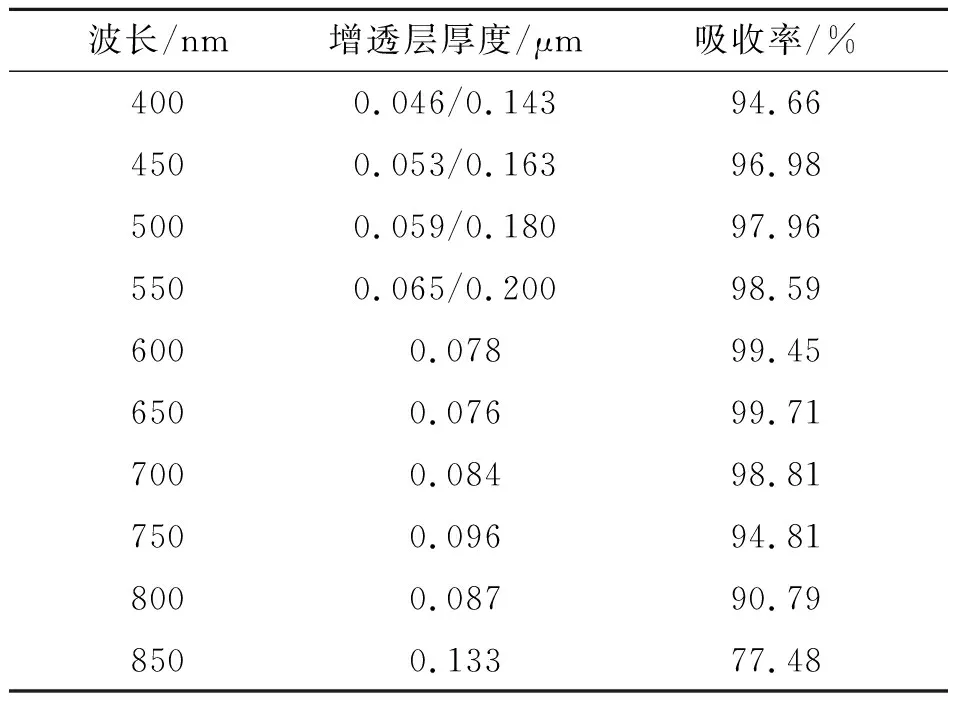
表2 单波长处吸收率峰值与增透层厚度的分布

4 结语

本文建立了多发射层AlGaAs基光电阴极的通用光学性质计算模型,并用该模型分别计算了宽光谱响应的GaAs光电阴极和532 nm敏感的窄带响应AlGaAs光电阴极的光学性质,其与试验曲线具有一致的变化趋势,仅出现部分可接受误差;试验验证了模型对于各种多发射层AlGaAs基光电阴极的有效性,而单发射层可以看作多发射层的简单情况;基于模型仿真计算了AlGaAs/GaAs光电阴极组件结构与400～900 nm波段各单波长光子吸收间的关系,分别探讨了0～2 μm的GaAs发射层、0～2 μm的AlGaAs发射层、0～0.2 μm的Si3N4增透层对单波长响应时光电阴极吸收率的影响.研究表明,同一波长响应下,GaAs发射层对光电阴极吸收率的影响最大,其次是Si3N4增透层,而AlGaAs发射层的厚度对吸收率的影响不明显.要得到90%以上的吸收率,在600 nm波长响应下要求发射层厚度大于0.5 μm,700 nm时应大于0.8 μm,800 nm时应大于1.5 μm.本文的研究结果可为不同需求下各类响应AlGaAs基光电阴极提供光学性质计算模型和结构设计的参考依据.