江西某钨矿山狭长型采空区胶结充填体强度设计

勒治华，王 廷，叶光祥，张 婷，张树标，聂亚林

（1.赣州有色冶金研究所有限公司，江西 赣州 341000；2.江西大吉山钨业有限公司，江西 全南 341802）

0 引 言

在地下金属矿山充填采矿中，充填体强度是充填技术的核心之一，其对充填质量、采场稳定性控制起着决定性作用，科学合理地确定实际工程中充填体所需强度至关重要。不同矿山的矿岩结构、围岩稳定性存在一定差异，采场或采空区内的充填体发挥的力学作用也不尽相同，不同强度的充填体发挥的轴向支撑或侧向约束作用也各不相同。因此，矿区充填体实际所需强度设计因矿山而异，主要取决于矿山开采技术条件、充填技术水平和充填材料强度特性等技术因素以及矿山开采成本与效益等经济因素[1-2]。

对于充填体强度设计，目前常用方法主要有：工程经验类比法[3]、理论分析计算法[4]、相似物理实验法[5]和数值模拟分析法[6]。其中，工程经验类比法是以经验为基础进行主观推导，理论分析计算法公式表达简洁明了，这两种方法使用简单，被广泛使用；相似物理实验法采用一定规模的物理模型，对已确定的矿山的开采条件、充填条件进行模拟，利用相似模拟的结果加以调整，推算被模拟矿山开采时的胶结充填体强度，这种方法使用过程复杂、结果误差较大；数值模拟分析法可以模拟时间顺序上各阶段的应力、应变变化情况，可在计算机中重演采场或采空区中充填体的受力前后的应力和应变状态。刘志祥等[7]基于建立的可靠度理论力学分析模型，对三山岛金矿深部采场充填体强度进行设计；张静等[8]通过室内充填配比试验，明确了红岭铅锌矿全尾砂废石胶结充填体的最佳配比；王志会等[9]建议使用三维极限平衡模型进行强度设计，并合理考虑采场动荷载、时间等因素；姜振兴等[10]结合经验类比法和理论分析法，设计了谦比希铜矿西矿体一步骤回采进路充填强度；董亚宁等[11]通过构建罗河铁矿高阶段采场充填体应力解析模型，计算获得不同采场高度条件下充填体最优强度；于永纯等[12]通过理论分析和数值模拟计算方法，确定了金厂河多金属矿空场嗣后充填法中窄长采场充填体所需强度为2.13 MPa；马生徽等[13]利用FLAC3D数值模拟优化了铜绿山矿上向分层充填法中胶结充填体强度，得到其平均强度为0.9 MPa。

本文以江西某钨矿山为工程依托，矿山拟通过建立胶结充填系统，实现有效治理原有采空区，以及空区充填后安全回采剩余矿产资源的目的。因此，本文根据矿区开采现状、地质条件，从采空区充填治理、充填采矿两个方面考虑，基于工程经验类比法和理论分析方法估算充填体强度设计理论值，并通过数值模拟的方法对充填体所需强度理论值进行验证，为矿区充填体强度设计提供参考依据。

1 工程背景

某钨矿山现有生产中段+517 m、+467 m、+417 m、+367 m、+317 m 和+267 m 中段，其中，+517～+367 m 中段南组区域已基本回采结束。现矿区拟通过建立胶结充填系统，对标高范围+267～+467 m（即+267 m、+317 m、+367 m 和+417 m 中段）的南组已有采空区进行充填处理，为深部矿产资源开发提供安全保障，以及在充填体的作用下，对+267 m、+317 m 和+367 m 中段剩余矿体进行回采，以满足矿山生产目标的要求。基于现场踏勘和采场设计资料收集，分别调查统计采空区治理标高范围+267～+467 m内采空区结构参数，如表1 所示。从表1 中可以看出，该矿区采空区呈多中段密集分布，采空区数量较多，且均符合狭长型采空区特征。

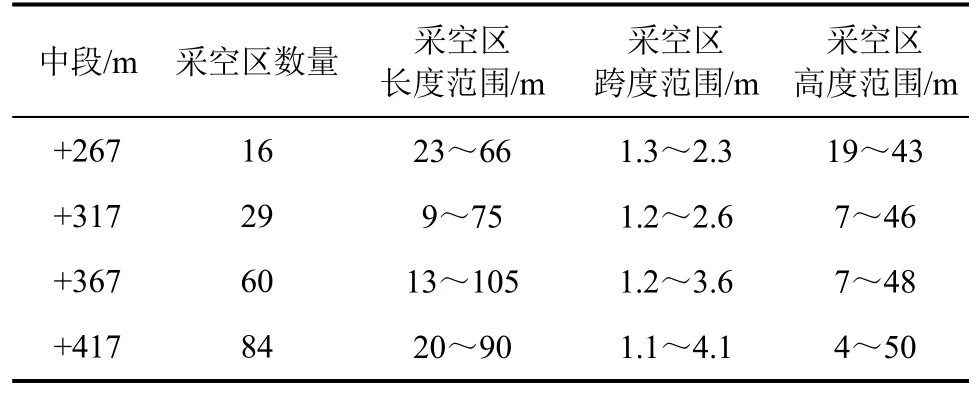
表1 采空区参数统计Tab.1 Parametric statistics of goaf

2 充填体强度分析

2.1 工程经验类比法

工程经验类比法主要是将所要设计矿山的开采与充填条件和相类似的矿山进行比较，从而选择一个认为较适当的充填体强度值。国内外不同矿山胶结充填体强度设计方法及设计值如表2 所示。根据矿山的实际条件与相类似矿山进行比较，筛选与该矿区工况相类似的矿山，通过类比分析矿区采空区结构参数（表2 中焦家金矿、洛各比矿和洼马拉矿）和充填材料选择，以及充填体所发挥的作用，初步选定该矿区采空区处理时胶结充填体设计强度为1.0～1.5 MPa。

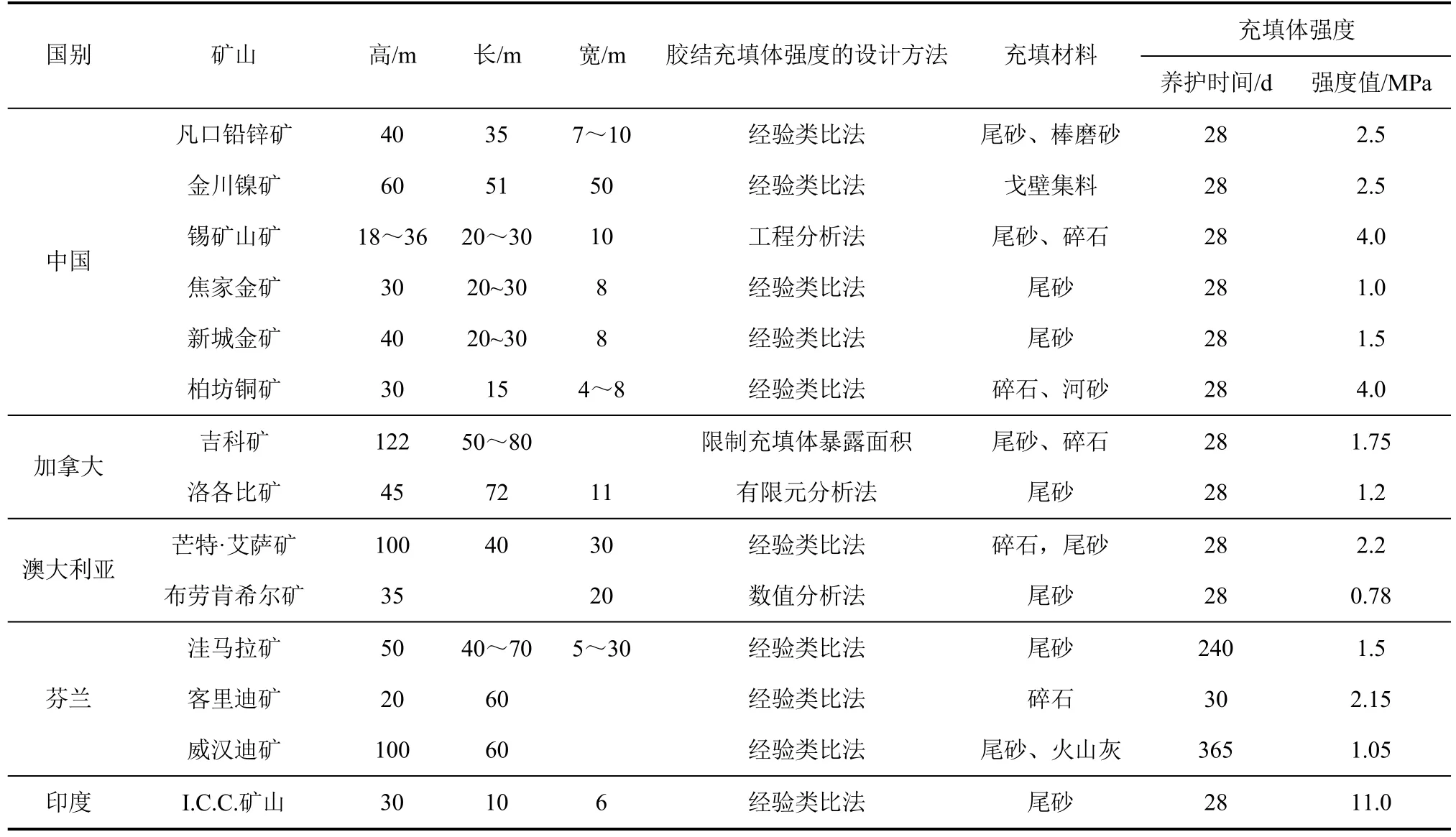
表2 国内外不同矿山胶结充填体强度设计方法及设计强度[14]Tab.2 Design method and strength of cemented back-filling in different mines at home and abroad

2.2 理论分析计算法

理论分析计算法是将充填体抽象成一个力学模型或模拟缩小的一个物理模型，通过推导出的充填体自立强度、支撑强度理论计算公式，根据采场结构参数和回采布置情况，计算得到充填体所需要的强度值。基于该矿区尾砂胶结充填体室内试验，得到不同灰砂比充填体强度力学参数，如表3 所示。根据工程经验类比法初选充填体强度 1.0 ～1.5 MPa，取灰砂比为1∶8 的充填体强度参数代入理论公式中估算充填体强度设计理论值。

表3 充填体物理力学参数Tab.3 Physical and mechanical parameters of cemented back-filling

2.2.1 采空区治理充填体强度需求

采空区充填治理时，空区充填体仅需满足自立强度即可，对于充填体自立强度设计，普遍采用的计算公式和力学模型方法有Terzaghi 模型法[1]、Thomas模型法[2]、卢平计算方法[15]和米切尔模型法[16]。

（1）Terzaghi 模型法

假设在距充填体顶部为H处，充填体所受的垂直应力分量为Vσ，其计算公式如式（1）所示。

式中：Vσ为充填体所受的垂直应力分量，MPa；L为充填体长度，m；H为距充填体顶部的距离，m；k为充填体侧压系数，，υ为充填材料的泊松比；φ为充填体内摩擦角，°；γ为充填体容重，MN/m3；C为充填材料的黏聚力，MPa。

充填体所受的垂直应力分量Vσ随充填长度和充填高度变化趋势如图1 所示，即充填体所需自立强度随充填体长度和高度的增大而增大。

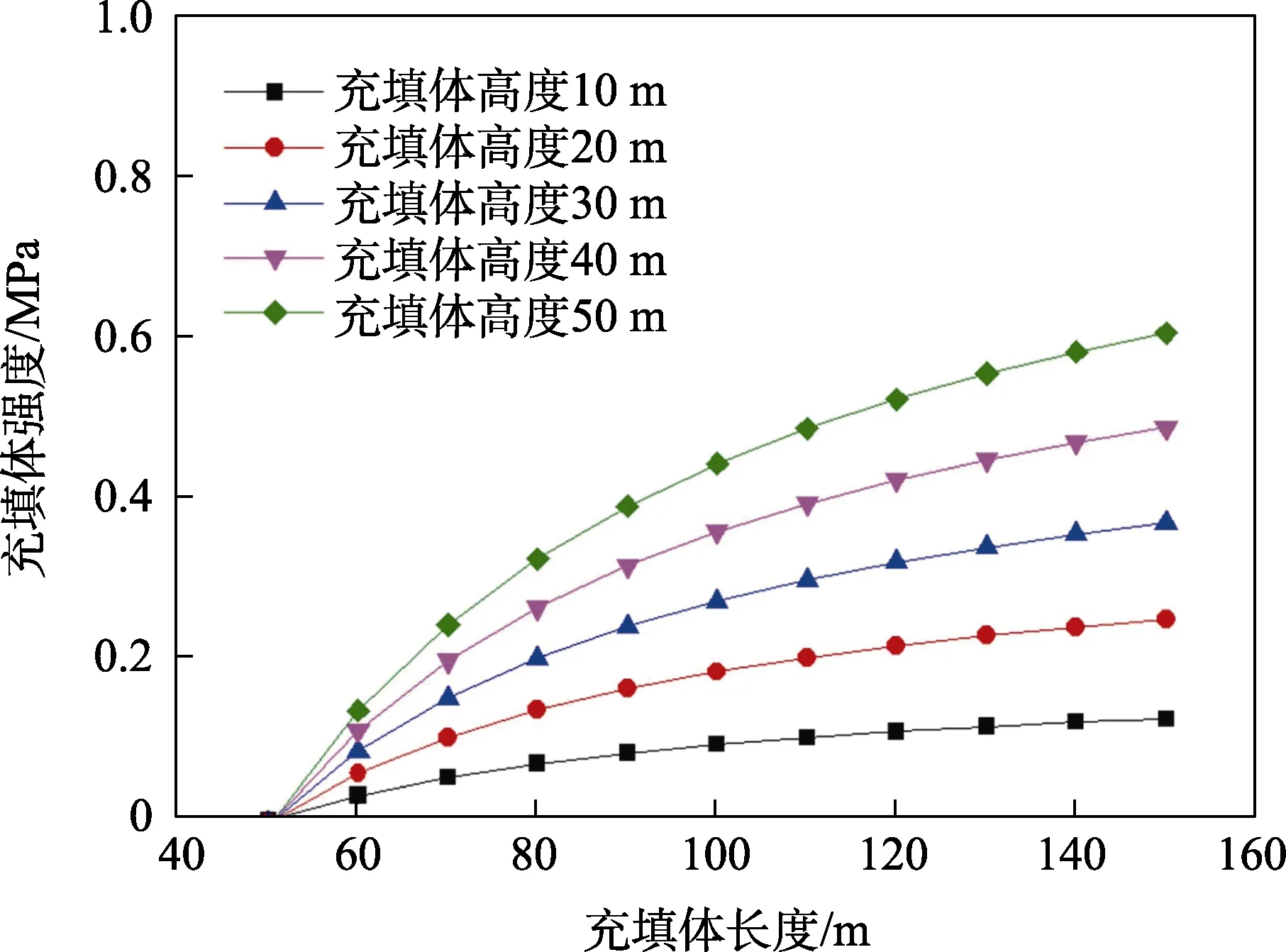
图1 Terzaghi 模型中充填体强度与充填长度和充填高度的关系Fig.1 Relationship between the back-filling strength and the filling length and height in the Terzaghi model

（2）Thomas 模型法

基于Thomas 模型算法得出充填体底板的垂直应力Vσ的计算公式如式（2）所示。

式中：Vσ为充填体底部的垂直应力，MPa；γ为充填体容重，MN/m3；h和b分别为胶结充填体高度和宽度，m。

充填体底部的垂直应力Vσ随充填高度和充填宽度变化趋势如图2 所示，即充填体所需自立强度随充填体高度和宽度的增大而增大。

图2 Thomas 模型法中充填体强度与充填高度和充填宽度的关系Fig.2 Relationship between the back-filling strength and filling height and width in the Thomas model

（3）卢平计算方法

卢平在Thomas 模型基础上，充分考虑充填体自身的强度特性，提出了修正模型（见式（3））。式中：σc为胶结充填体的设计强度，MPa；γ为充填体容重，MN/m3；h和b分别为胶结充填体高度和宽度，m；k为充填体侧压系数，k=1-φ1，φ1为充填体与围岩间的摩擦角；α为充填体滑动面与水平面的夹角，α=45°+φ/2，φ为充填体内摩擦角，°；C1为充填体与围岩间的黏聚力，MPa；C为充填体的黏聚力，MPa。

充填体设计强度随充填高度和充填宽度的变化趋势如图3 所示，即充填体所需自立强度随充填体高度和宽度的增大而增大。

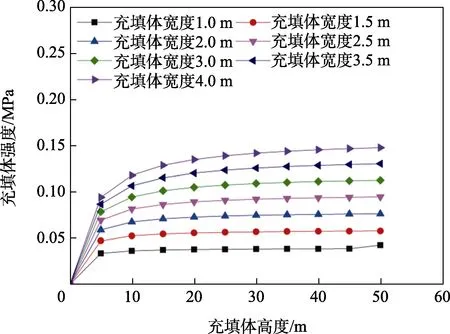
图3 卢平计算方法中充填体强度与充填高度和充填宽度的关系Fig.3 Relationship between the back-filling strength and filling height and width in the Lu Ping's calculation method

（4）米切尔模型法

基于米切尔模型，单侧竖向揭露充填体安全系数SF计算公式如式（4）所示。

式中：FS为单侧竖向揭露充填体安全系数；φ为充填体内摩擦角，°；α为充填体潜滑面与水平面的夹角，α=45°+φ/2；L和B分别为充填体长度和宽度，m；H*为楔形滑体等效高度，H*=H-0.5Btanα，H为胶结充填体的高度，m；γ为充填体容重，MN/m3；cs为充填体与围岩间的黏聚力，MPa；c为充填体的黏聚力，MPa。

在公式（4）的基础上，假设采空区岩壁十分粗糙，接触面与充填体黏聚力相等[17]，取cs=c，则充填体黏聚力可表示为式（5）。

从式（5）可得极限平衡状态（FS=1）下充填体强度要求的黏聚力，假设充填体服从直线型摩尔库伦准则，则充填体单轴抗压强度可表示为式（6）。

充填体设计强度σc随充填长度和充填宽度的变化趋势如图4 所示，即充填体所需自立强度随充填体长度的增大而增大，随充填体宽度的增大而减小。

综合上述理论公式充填体自立强度随充填高度、充填长度、充填宽度变化趋势，以及该矿区各中段采空区（充填体）结构参数范围统计和充填体强度参数，可得矿区各中段充填体所需自立强度理论值范围，根据刘光生浮动安全系数方法[18]，考虑安全系数FS=2，选择充填体所需自立强度理论取值范围，如表4 所示。从表4 可知，充填体自立强度设计值为0.032～1.177 MPa，从安全角度考虑，建议取其设计强度大于1.177 MPa，该结果满足工程经验类比法中充填体强度设计取值。

表4 各中段充填体所需自立强度理论值Tab.4 Self-supporting strength theoretical value of cemented back-filling in each level

2.2.2 剩余矿体回收时空区充填体强度需求

矿区拟对+267 m、+317 m、+367 m 和+417 m中段采空区充填治理后，在充填体的作用下回采+267 m、+317 m 和+367 m 中段剩余矿体，即可将原有空区采矿作业视为一步骤采矿作业，剩余矿体回收视为二步骤采矿作业，在二步骤回采时，原本施加在二步骤采场的压力转移到一步骤采空区充填体上，即一步骤采空区充填体起支撑顶板岩层压力的作用，充填体支撑强度常采用扩大压力拱理论来分析，充填体柱承受载荷的计算公式见式（7）[19]。

式中：P为充填体柱承受载荷，MPa；a和b分别为一步骤和二步骤回采宽度，m；γ为上覆岩层平均容重，kN/m3；W为整个扩大压力拱跨度，m；B为开采区域总宽度，m；h为充填高度，m；fk为覆岩的坚固性系数，其值为整体岩石单轴抗压强度的十分之一；k为压力拱修正系数。

由公式（7）可知，充填体所需支撑强度与一步骤和二步骤回采宽度密切相关，其相应的变化趋势如图5 所示，充填体所需支撑强度随一步骤回采宽度增大而减小，随二步骤回采宽度增大而增大。

图5 扩大压力拱理论中充填体所需强度与一步骤和二步骤回采宽度关系Fig.5 Relationship between the back-filling strength and the width of one-step and two-step mining in the expanded pressure arch theory

根据现场剩余矿体赋存条件，现拟采用小采和大采两种采场结构参数对剩余矿体进行回采，其本质区别在于采场跨度的差异。当两条矿脉相距较远（大于5 m 左右），且中间夹层岩石稳固性较好，则采用小采的方式，此时采场跨度一般为1.2～2.5 m；当两条矿脉相距较近（小于5 m 左右），且中间夹层岩石破碎、稳固性较差，则采用大采的方式，此时采场跨度一般不大于10 m。因此，在+267 m、+317 m 和+367 m 中段进行剩余矿体回收时，二步骤采场最大跨度不大于10 m。因此，根据扩大压力拱理论公式，可得各中段剩余矿体回收时一步骤充填体所需支撑强度理论值范围，如表5所示。

表5 各中段充填体所需支撑强度理论值Tab.5 Support strength theoretical value of cemented back-filling in each level

综上计算，需要进行二步骤回采剩余矿体时，一步骤采空区充填体所需支撑强度设计值为0.767～2.286 MPa，在扩大压力拱理论中，基于极限强度理论的一步骤充填体稳定性判别条件，根据比涅乌斯基计算公式[20]，一步骤充填体的强度大于或等于1.5 倍的其可承受的最大载荷，因此，考虑安全系数Fs=1.5，从安全角度考虑，建议取其设计强度≥3.429 MPa。

3 充填体强度数值模拟验证

3.1 计算模型构建及力学参数

本文采用FLAC3D数值模拟软件分析充填采空区围岩和充填体中位移与应力分布情况，验证矿区充填体强度设计所需理论值。基于Rhino 和Griddle软件进行构建矿区南组三维模型，模型包括+267 m、+317 m、+367 m、+417 m 和+467 m 五个中段矿脉及周边围岩，模型整体选取沿矿体走向方向为X 轴方向，垂直矿体方向为Y 轴方向，垂高方向为Z 轴方向，模型X 轴方向由西十一线至东三线，共700 m长度，模型Y 轴方向长度为250 m，模型Z 轴方向从+217 m 至+517 m，共300 m 高度，即最终模型尺寸为700 m×250 m×300 m，如图6 所示；数值计算模型为四面体单元，且一共划分单元数为905 525个，节点数为148 125 个。

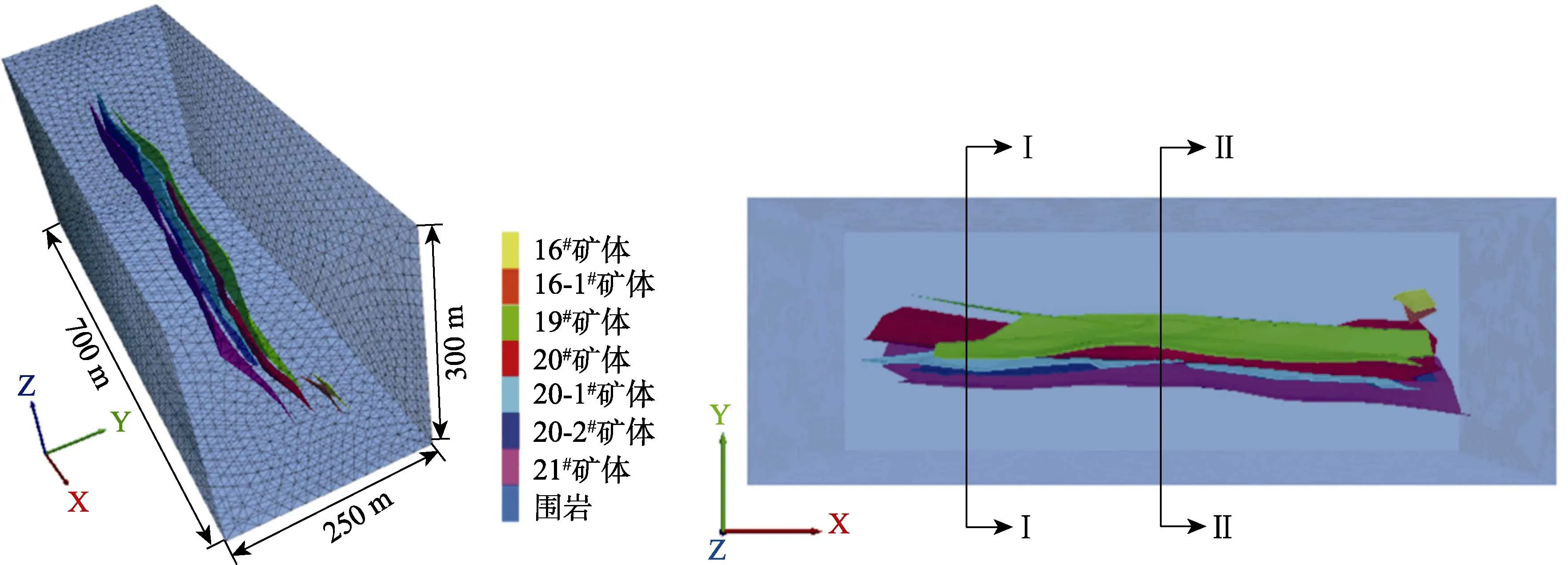
图6 三维数值模型Fig.6 3D numerical model

边界条件：模型底部水平、竖直方向位移约束，模型四周水平方向位移约束，模型顶部施加10.6 MPa 外载荷模拟上覆岩层压力（模型顶部标高+517 m，根据矿区地形图，南组地表最大标高超过900 m，即P=γH=27.86 ×(900 -517) ×10-3=10.6 MPa）。

屈服准则：模型计算时，矿岩本构模型采用Mohr-Coulomb 弹塑性模型。

力学参数：模型中矿岩力学参数通过矿山已有资料获取，如表6 所示，对矿区不同强度充填体强度参数选取如表7 所示。

表6 矿体围岩力学参数Tab.6 Mechanical parameters of ore and rock

表7 充填体力学参数Tab.7 Mechanical parameters of back-filling

3.2 模型初始应力平衡

数值模拟计算时，根据实际采空区分布情况，一次性开挖矿体形成采空区，开挖后运行20 时步模拟采空区的形成，随后进行充填。图7 为模型Z 方向的应力和位移初始平衡云图，可以看出应力和位移均随着埋深的增大均匀增加，且呈层次分明的上下均匀的层状分布；模型的初始应力平衡状态结果表明开采前地层未受扰动，与实际情况相符。

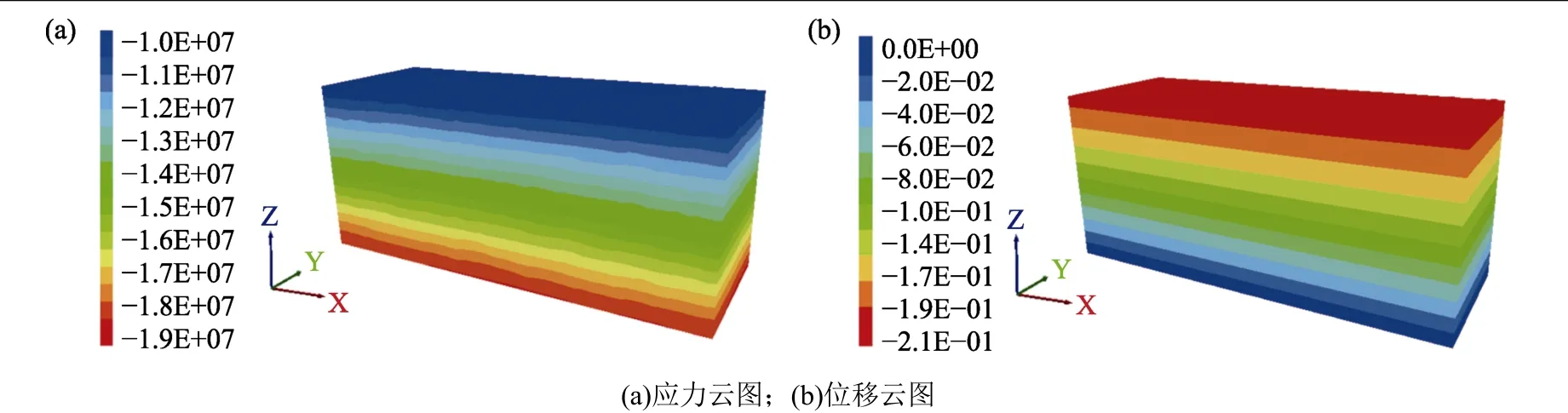
图7 初始应力平衡状态下Z 轴方向应力和位移云图Fig.7 Z-axis stress and displacement nephogram under initial stress equilibrium state

3.3 采空区治理时充填体强度数值模拟验证

图8 为采空区不充填和不同充填体强度下最小主应力云图（剖面I-I），可知，采空区充填可以显著改善周围岩体的应力状态，且随着充填体强度的增大，围岩应力集中的程度逐渐减弱，但充填体强度对应力的分布形式影响较小；图9 为采空区不充填和不同充填体强度下位移云图（剖面I-I），从图9 中可以看出，由于充填体的充入，采空区上部垂直位移明显得到了有效抑制，且随着充填体强度的增大，充填体及围岩变形逐渐降低，以及采空区上部变形范围也呈逐渐减小的变化趋势。对比分析图8 和图9 可明显发现，随着充填体强度的增大，围岩最小主应力值和分布范围，以及充填体和围岩的变形均逐渐减小，且当充填体强度达到1.27 MPa后，充填体强度对围岩最小主应力值和分布范围，及其对充填体和围岩的变形影响不大。

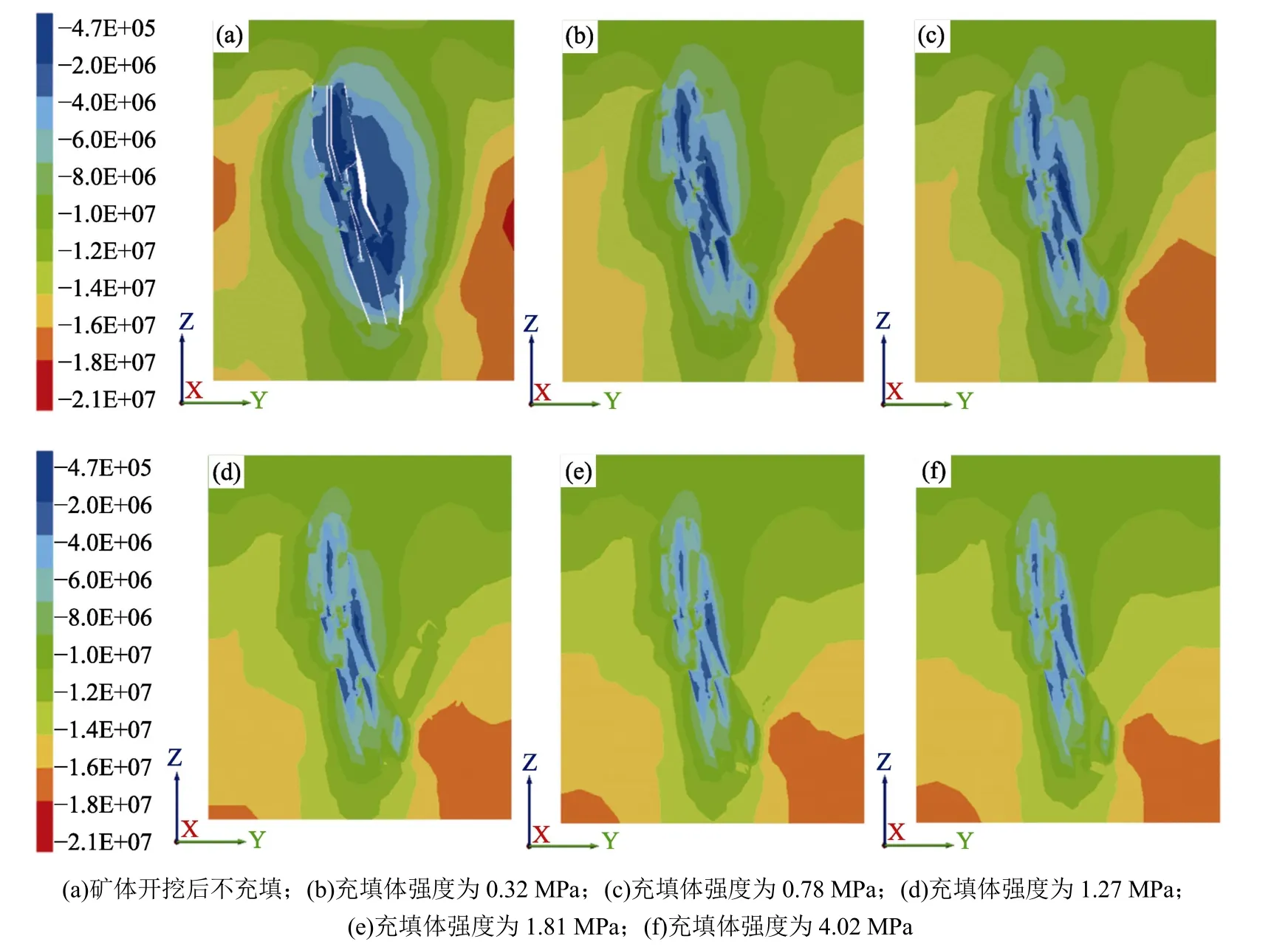
图8 不同充填体强度下最小主应力云图Fig.8 Minimum principal stress cloud diagram with different back-filling strengths in goaf

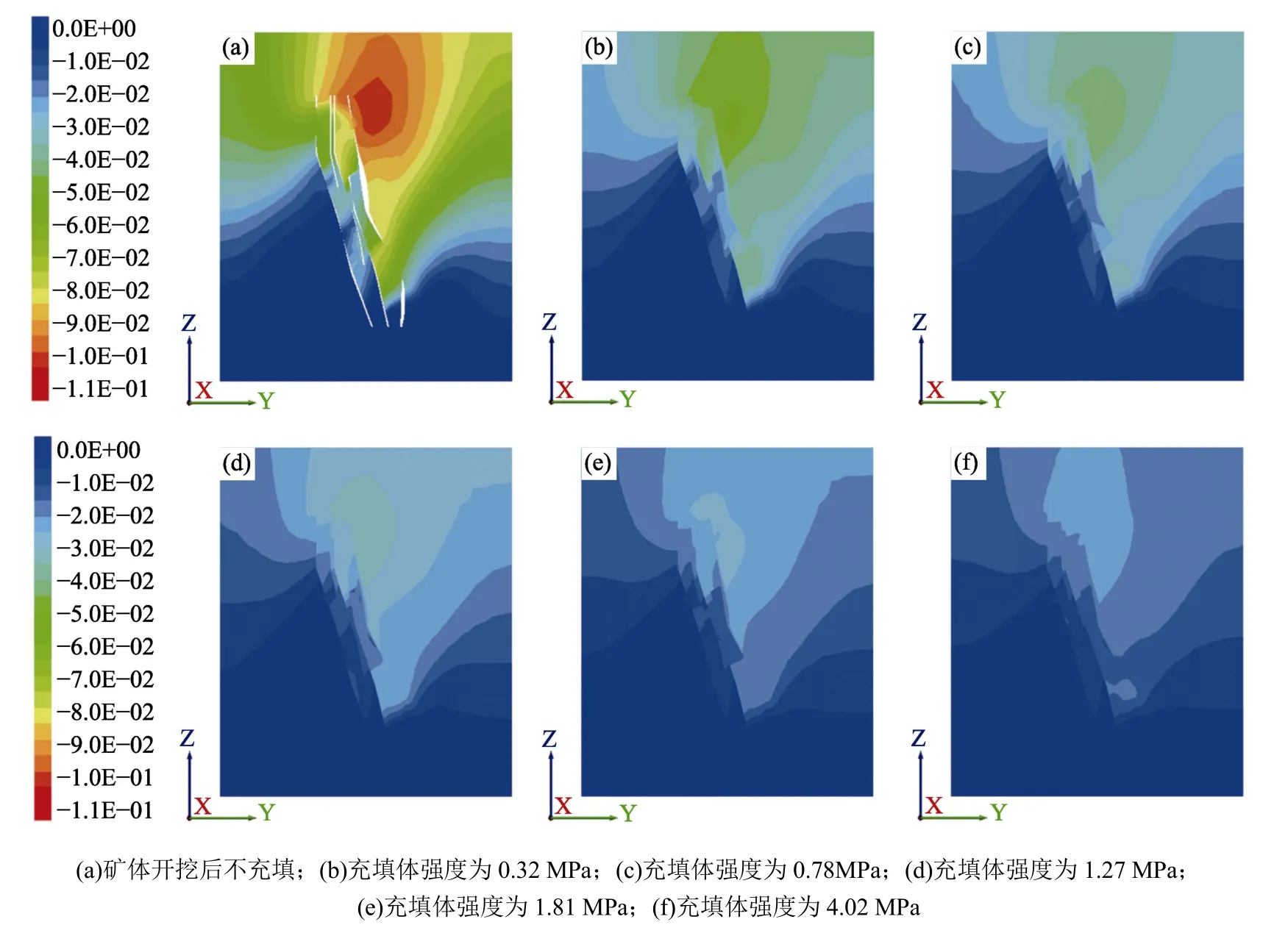
图9 不同充填体强度下位移云图Fig.9 Displacement cloud diagram with different back-filling strengths in goaf

此外，取上盘围岩矿体高度1/2 位置处竖向垂直位移和水平位移，如图10 所示，围岩垂直位移和水平位移均随充填体强度的增大而减小，当充填体强度由0.32 MPa 增加到1.27 MPa 时，围岩垂直位移由0.038 5 m 降低到0.026 m，而水平位移由0.025 4 m 降低到0.013 8 m，分别降低了32.5 %和45.7 %；当充填体强度继续增加至4.02 MPa 时，围岩垂直位移和水平位移继续分别降低至0.021 9 m和0.011 5 m，位移总体降幅不大，即当充填体强度达到1.27 MPa 后，其整体表现出逐渐收敛的变化趋势。

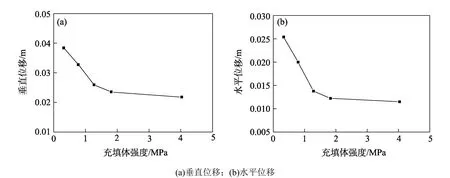
图10 矿体高度1/2 位置处上盘围岩位移与充填体强度变化Fig.10 Relationship between the back-filling strength and the displacement of hanging wall surrounding rock at the 1/2 position of orebody height

综上，基本验证了采空区充填治理时充填体所需理论强度设计值1.177 MPa。

3.4 剩余矿体回收充填体强度数值模拟验证

在模拟计算原有采空区充填后剩余矿体回收时，原有采空区开挖并充填后，随后开挖剩余矿体（剩余矿体之间的围岩同时被视为开挖矿体），且不进行充填。图11 为原有采空区充填后剩余矿体回收时不同充填体强度下最小主应力云图（剖面II-II），可知，随着充填体强度的增大，空区围岩应力集中的程度有减弱的趋势，但不是很明显；图12为原有采空区充填后剩余矿体回收时不同充填体强度下位移云图（剖面II-II），随着充填体强度的增大，充填体及围岩的变形和位移量逐渐降低；同时，当充填体强度不大于1.81 MPa 时，其最大垂直位移发生在原有空区充填体上，当充填体强度为4.02 MPa 时，最大垂直位移发生在剩余矿体开挖后形成的空区顶板位置处，表明此时充填体能很好地起到了支撑作用。

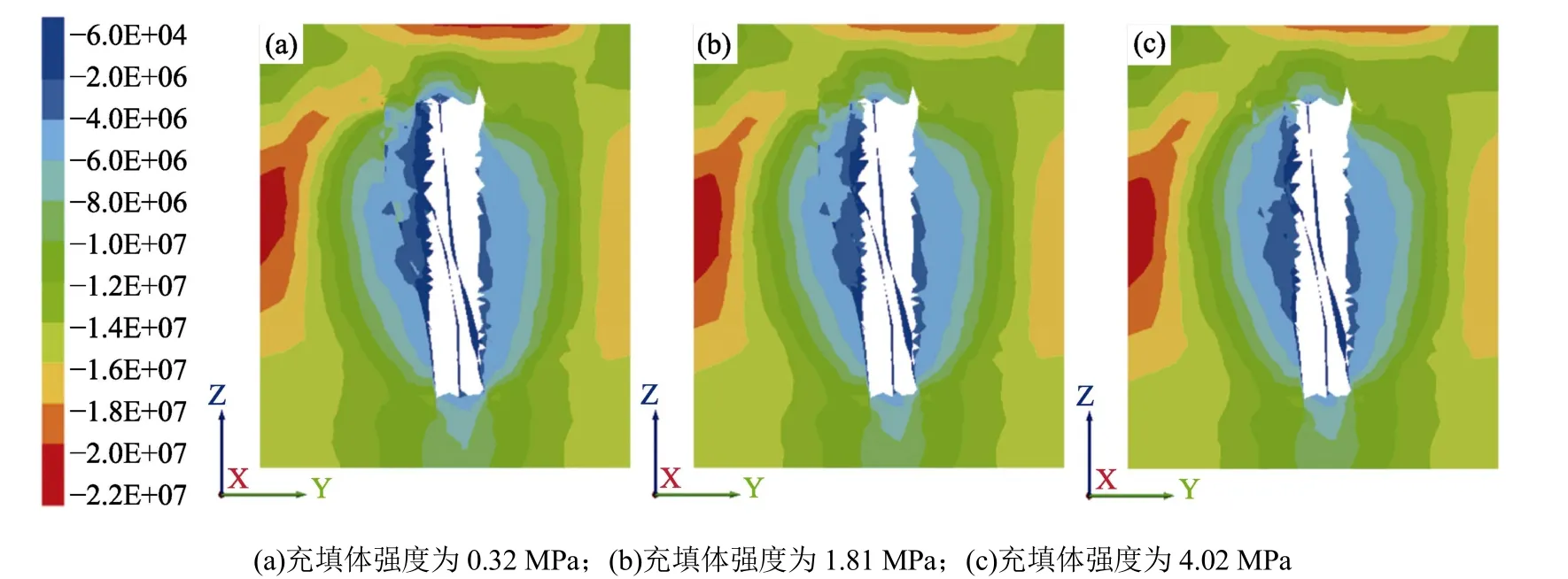
图11 原有采空区充填后剩余矿体回收后不同充填体强度下最小主应力云图Fig.11 Minimum principal stress cloud diagram with different back-filling strengths of original goaf after residual ore body recovery

图12 原有采空区充填后剩余矿体回收后不同充填体强度下位移云图Fig.12 Displacement cloud diagram with different back-filling strengths of original goaf after residual ore recovery

由图12 可知，当充填体强度为1.81～4.02 MPa之间某一值时，原有空区充填体开始发挥支撑作用，为进一步确定该充填体强度值，补充原有空区充填体强度为3 MPa 和3.5 MPa 的模拟方案。两种工况下位移云图如图13 所示，结果表明，当原有空区充填体强度达到3.5 MPa 后，充填体开始提供支撑作用，剩余矿体回收时原有采空区充填体所需理论强度值3.429 MPa 得到了很好的验证。

图13 补充方案位移云图Fig.13 Displacement cloud diagram of supplementary scheme

4 结 论

（1）通过工程经验类比法初选某钨矿山胶结充填体设计强度为1.0～1.5 MPa，且基于采空区治理时充填体自立强度计算理论公式，得到充填体所需自立强度设计理论值应≥1.177 MPa；数值模拟采空区治理结果表明，随着充填体强度的增大，围岩最小主应力值和分布范围以及充填体和围岩的变形均逐渐减小，但当充填体强度达到1.27 MPa 后，围岩和充填体的应力和变形表现出逐渐收敛的变化趋势，即该矿区采空区充填治理时充填体强度设计理论值≥1.177 MPa 基本得到了验证。

（2）基于扩大压力拱理论，估算得到剩余矿体回收时采空区充填体所需支撑强度理论值应不小于3.429 MPa；通过数值模拟原有空区一步骤开挖充填，剩余矿体二步骤回采，发现当一步骤充填体强度达到3.5 MPa 后，充填体开始提供支撑作用，基本验证了该矿区剩余矿体回收时充填体强度设计理论值不小于3.429 MPa。