混合模式搜索差分进化算法研究及其在高压容器概率优化中的应用

赵 晖，卢青波

（1.西安鑫垚陶瓷复合材料股份有限公司，西安 710100；2.郑州职业技术学院机械工程系，郑州 450121）

随着现代化学工业的快速发展，高压容器越来越得到广泛应用，如合成氨工业、合成尿素工业、合成甲醇工业和石油加氢工业等，其合成反应装置不仅压力高（p≥15 MPa），而且常伴有高温，如合成氨就常在15～32 MPa压力和500 ℃高温下进行合成反应。由于化工设备的大型化，高压容器的大型化也是必然趋势，从而导致容器的直径、壁厚及质量越来越大。在保证高压容器安全运行的基础上，利用现代优化设计理论及方法对高压容器进行全面综合分析，对高压容器筒体进行优化设计，减少制造成本和耗材，具有实际意义和工程价值。

工程结构和机械设计中的不少问题都含有一些不可忽视的随机因素，如工作载荷、风载荷或地震载荷；材料的物理和力学性质，如强度、弹性模量等。在这种情况下，设计者应考虑若干随机因素下做出最佳决策。压力容器设计中，容器内的压力和所用材料的屈服强度极限及容器的尺寸都呈现出随机因素。常规设计中，采用安全系数的方法，通过适当增加或减少设计的名义值来保证设计的可靠性，但这种设计几乎都是根据设计师的经验或者直觉判断进行的，是否能达到最优设计是值得商榷的。因此，本文拟从概率角度建立高压容器的优化模型，并且采用混合差分进化算法对所建立的模型进行求解。

差分进化算法（Differential Evolution，DE）[1]使用简单的变异、交叉及竞争算子实现在连续空间中的随机搜索。DE 算法原理简单，易于实现，在许多复杂优化问题中得到了应用[2-6]。DE 算法同其他进化算法类似，需要平衡算法的全局搜索能力与其收敛速度。这种平衡可以通过调节算法的控制参数来实现，但往往控制参数的调节效果有限。因此，许多学者从不同类型算法的优势出发，结合随机优化算法的全局性能和局部优化算法的局部搜索能力，研究提出了不同的混合优化算法[7-8]。模式搜索算法（Pattern Search，PS）是一种直接优化方法，无须求解目标函数的导数，算法简单且具有良好的局部搜索能力[9]。因此，很多学者将模式搜索算法与进化算法相结合，提出了新的混合算法[10-14]。本文拟将PS 算法引入到DE 算法的DE/rand/1/bin 模式中，研究提出一种基于模式搜索算法的混合差分进化算法——混合模式搜索差分进化算法（Hybrid Pattern Searching Differential Evolution algorithm，HPSDE）。该混合算法利用了DE 算法良好的全局搜索能力和PS算法快速的局部搜索能力，将两者的优势相结合，较大地提升了算法的寻优效率。

1 混合模式搜索差分进化算法建模

1.1 差分进化算法

DE 算法的进化个体采用实向量进行编码，采用均匀分布的随机数产生初始个体。令xi（g）代表第g代的第i个个体，其中，分别为个体的上、下限，则

式中：NP 为种群大小，Tmax为最大进化代数。

DE 算法就是由这NP 个个体构成的种群在搜索空间不断进化来进行寻优的。DE 算法候选解产生模式有很多种策略[1]，其中DE/rand/1/bin 策略应用较为广泛，且具有全局搜索能力较好、收敛速度较慢的特性，因此，本文选择该进化模式为研究对象。以求解最小值问题为例说明差分进化算法的进化过程如下。

1）初始化种群。在n维实数空间按式（2）随机产生NP 个个体

式中：rand（0，1）是[0，1]上服从均匀分布的随机数。

2）变异算子。首先随机从种群中选择3 个不同个体xp1，xp2，xp3，且p1≠p2≠p3≠i则变异算子为

式中：F 为缩放因子。

3）交叉算子。交叉算子可以增加种群的多样性，其操作过程如式（4）所示。

式中：CR 为交叉率，CR∈[0，1]，jrand是[1，n] 上的随机整数，这种交叉模式确保νij（g+1）中至少有一位来自hij（g）。

4）选择算子。DE 算法的选择策略采用“贪婪”策略，由评价函数对向量νi（g+1）和向量xi（g）比较，保留较优个体，即

反复执行式（3）到（5），直到达到算法预设的终止条件。

1.2 模式搜索算法

PS 算法是一种典型的直接搜索方法，同样不依赖于梯度信息，具有明显的几何意义和快速收敛特性。PS算法的包含探测与移动2 个操作过程。探测的目的是寻找目标函数值较优的下一个点，其过程为从当前点出发，依次在n维空间进行探索。移动过程的目的是实现较优点的加速，即以探索到的点为基点，查找该点的下一个较优点。从几何意义上讲，PS 算法就是从当前位置开始，寻找比当前位置较优的位置，并沿着该方向继续搜索，实现向目标函数的不断逼近。模式搜索算法的步骤如下。

若开始点和开始步长分别为x(1)和d，e1，e2，…，en是坐标向量，计算精度和加速因子分别为ε 和γ。

Step1 记y(1)=x(1)，k=1，j=1；

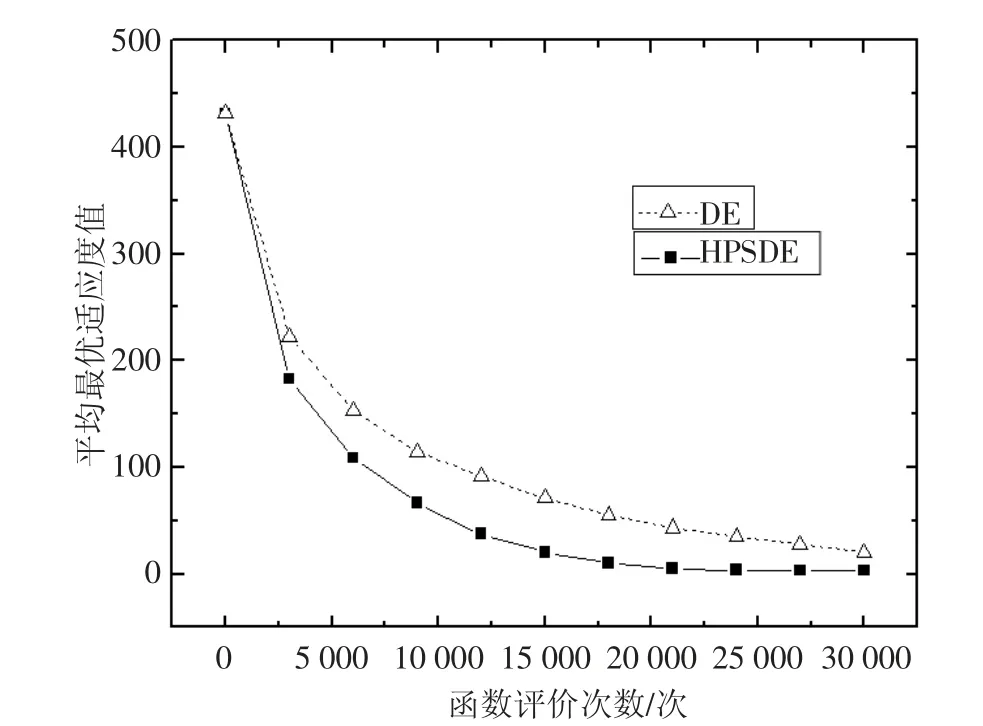
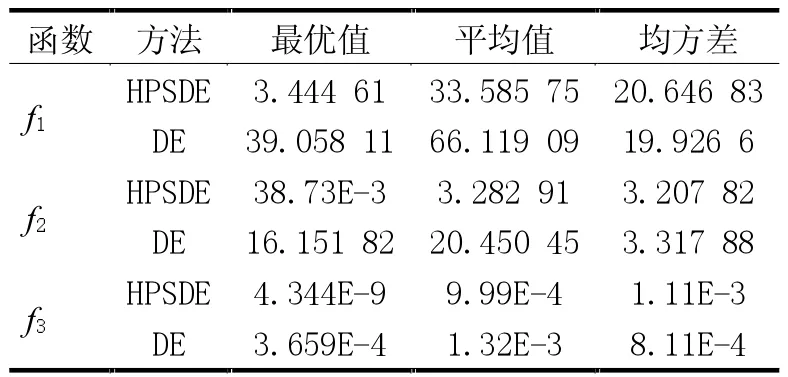
Step3 若j

若f(y(n+1))≥f(x(k) )，执行Step5；

若f(y(n+1))＜f(x(k) )，执行Step4；

Step4 记x(k+1)=y(n+1)，

y(1)=x(k+1)+γ x(k+1)-x(k)()，k=k+1，再记j=1，转Step2；

Step5 若d≤ε，则计算结束，记x*=x(k)；否则，记d=d/2，y(1)=x(k)，x(k+1)=x(k)，k=k+1，再记j=1，转Step2。

PS 算法的搜索步长在各个方向是相同的，这就使模式移动方向与最优下降方向的偏差较大，从而制约了算法的收敛速度和精度，且使算法对初始点的敏感度增强。因此，在模式搜索差分进化算法中，模式搜索的初始点选择为当前种群的最优点。

在采用最优步长的坐标轮换方法中，若把前一轮的搜索末点xq与这一轮的搜索末点xh连接成一向量s=xh-xq，沿此方向进行搜索，显然，可以大大加快收敛速度，因此，在模式搜索中，选择当前群体除群体最优个体之外的所有个体的中心点为前一轮的搜索末点，式（6）定义了其计算方法。当前群体的最优点为这一轮的搜索末点构成搜索方向向量。取该方向向量的每一维，构成坐标向量。取步长d为[0，1]上服从均匀分布的随机数。

由于HPSDE 算法的步长因子设置为[0，1]上的均匀分布的随机数，因此，PS 算法的Step5 中的终止条件无法实现，为此，设置PS 算法的Step5 为记x*=x(k)，PS算法终止。修正后的PS 算法的步骤如下。

Step2 若f(y(j)+dej)

Step3 若j

否则j=n，若f(y(n+1))≥f(x(k) )，转Step5；若f(y(n+1))

Step4 记x(k+1)=y(n+1)，

y(1)=x(k+1)+γ (x(k+1)-x(k))，k=k+1，再记j=1，转Step2；

Step5 记x*=x(k)。

1.3 混合模式搜索差分进化算法

DE 算法的变异策略有多种，其中DE/rand/1/bin变异策略具有全局搜索能力强、收敛速度慢的特性。由式（3）可知，DE/rand/1/bin 变异过程中，其候选解的产生采用的是种群中随机选择的3 个不同个体，通过线性运算产生的。该变异过程并没有考虑所选择个体的适应度信息，随机性强，有利于保持种群的多样性，但同时也使算法的收敛速度较慢。DE 算法的随机搜索过程，有可能导致已经找到最优解附件的点，但由于随机选择的交叉个体的原因，而错过真正的最优解。此时，若能在最优解附近利用一些局部搜索能力强的算法对最优解附近进行局部搜索，则对于提升算法的全局搜索能力，找到全局最优解是有帮助的。

因此，若当前种群的群体最优个体连续m次目标函数评价（如100 次目标函数评价）没有改进时，以当前种群最优个体为基点，以PS 算法进行局部搜索，搜索到的较优点或次优点与群体最差点进行竞争，从而实现对群体点的改良，促使种群继续进化。若在连续m代内当前种群最优个体有所提升，表明DE 算法正常进化，无停滞现象发生，正朝着全局最优解的方向逼近，此时，不必加入局部搜索策略。HPSDE 算法正是基于以上思想进行设计的，其实现步骤如下。

Step1 设置种群规模NP、交叉概率CR、缩放因子F，计算精度ε 及加速因子γ，在参数空间随机初始化每一个个体，设置最大进化代数为T，令t=1。

Step2 计算当前种群的最优适应度bestfitness 及最优个体。

Step3 若最优适应度bestfitness 达到精度要求或者迭代次数达到最大，则输出当前最优适应度值，退出；否则，转Step4。

Step4 若当前最优适应度bestfitness 连续m次目标函数评价没有得到改进，则执行Step5，否则，执行Step7。

Step6 以当前群体最优点为初始点，执行模式搜索算法，并将最优结果替换当前群体中的最差点。

Step7 对群体中的所有个体执行

Step7.1 执行式（3）的变异算子。

Step7.2 执行式（4）的交叉算子。

Step7.3 执行式（5）的选择算子。Step8t=t+1，转Step2。

2 混合模式搜索差分进化算法性能分析

为验证HPSDE 算法的有效性，采用以下3 个典型的测试函数，与DE 算法（DE/rand/1/bin 模式）进行比较。

实验中算法的相关参数设置为种群规模设置为50，F 设置为0.5，CR 设置为0.1。HPSDE 算法触发PS算法的临界条件为连续100 次函数评价次数没有更新，且为使PS 算法能够具有更强的勘探能力，且又不会远离当前点，设置加速因子γ 为1.2。为了使算法的比较更公平，采用函数评价次数为终止条件，总的函数评价次数设置为3e5 次。为避免实验结果的随机性，DE 算法与HPSDE 算法对每个函数均独立运行30 次，统计结果见表1。图1—图3 为30 次实验平均最优适应度进化曲线，图中横坐标为函数评价次数，纵坐标为对应的30 次实验平均最优适应度值。

图1 f1（x）30 次平均适应度进化曲线

图2 f2（x）30 次平均适应度进化曲线

图3 f3（x）30 次平均适应度进化曲线

表1 HPSDE 与DE 运行30 次的函数优化结果比较

2.1 性能分析

HPSDE 算法的设计思想是在DE 算法中协同PS 算法，使PS 算法能够帮助DE 算法进行精细搜索，从而提升DE 算法的搜索精度。初始进化阶段，由于DE 算法种群多样性较好，个体进化较快，一般不会出现停滞现象，HPSDE 算法中PS 算法不会发挥作用。进化的中后期，种群的多样性下降，出现进化停滞现象，即连续多次函数评价（如100 次函数评价）种群最优解得不到改进，此时，PS算法开始发挥其作用，以当前最优解为基点执行PS 算法，并使PS 算法搜索结果替换当前种群中最差个体，从而加快算法的收敛速度。同时，由于PS 算法的搜索基点为当前的群体最优点，因此，这种局部搜索会帮助DE 算法提升其搜索精度。但由于有新的搜索策略的引入，且新策略的更新机制使种群中的个体得到更新，因此会破坏DE 算法的原有进化过程，影响DE 算法的稳定性。

2.2 结果分析

从表1 最优值数据与平均值数据可以看出，在相同的函数评价次数下，HPSDE 算法的求解精度要优于DE 算法的收敛精度，表明DE 算法在引入了PS 算法之后，其收敛速度得到了提升。从30 次最优值的均方差比较可以看出，HPSDE 算法的均方差在函数f1和f3求解结果上要差于DE 算法的结果，在f2的求解结果上要优于DE 算法，表明PS 算法受初始解的影响较大，尽管PS 的初始解为当前DE 算法的最优解，但若当前解的周围不存在优于当前群体最差解的解时，则会使DE 算法的函数评价次数减少，影响到某次最优解的精度，使均方差的结果变差，从而使算法的稳定性降低，与算法性能分析结果一致。

从图1—图3 可以看出，HPSDE 算法的收敛速度要明显优于DE 算法；进化开始阶段，DE 算法收敛速度较快，能够不断地提升寻优精度，不断地向全局最优解逼近，在此过程中没有出现进化“停滞”现象，PS 算法不会被触发，因此，不会发挥作用，从而，HPSDE 算法和DE 算法的收敛曲线具有极大的相似性。但随着DE 算法进化停滞，连续多代种群的最优解得不到改进，PS 算法以当前群体最优解为基点进行局部搜索，并使搜索结果替代当前种群中最差个体，加快了DE 算法的收敛速度。

3 高压容器概率优化案例及分析

图4 为压力容器的结构尺寸与内压的概率密度函数曲线[15-16]。根据现场抽样检查得到表2 所列数据。其中p为容器的工作压力，σs为材料的屈服强度极限，h为钢板厚度。确定该容器在满足强度不失效概率为0.95 下的最大容积的尺寸R和H，且要求容器尺寸限制在2≤H/R≤2.5。

图4 压力容器的结构尺寸与内压概率密度函数曲线

表2 压力容器设计的已知数据

考虑到压力容器制造的工艺误差，认为压力容器的设计尺寸R和H是服从正态分布的随机变量，其均值μR和μH是未知的，其标准差取为σR=0.03μR，σH=0.03μH。这样设计变量为x=[x1，x2]T=[μR，μH]T。

随机参数为容器内的工作压力p、容器的壁厚h及材料的允许强度极限σs，即

目标函数取为压力容器的容积，即

约束函数为

由此可建立压力容器的概率优化设计的数学模型为

设置HPSDE 算法的种群规模为50，最大函数评价次数为2e5 次，F 为0.5，CR 为0.1。HPSDE 算法触发PS 算法的临界条件为连续100 次函数评价次数没有更新，加速因子γ 为1.2。表3 给出了压力容器的优化设计结果。

表3 压力容器的优化设计结果

从表3 的优化结果可以看出，对于含有随机因素的优化问题，用一般优化设计方法所得结果是十分不可靠的。因为其约束满足的实际概率值仅有50%左右。若用随机模型进行优化设计，且采用其计算结果比较合理与可靠。

4 结论

本文首先通过对差分进化算法及模式搜索算法研究，提出了一种混合模式搜索差分进化算法，通过仿真实验对算法性能进行了分析，发现该算法在相同的函数评价次数下，HPSDE 算法的求解精度要优于DE 算法的精度。但在一定条件下，PS 算法的引入又会使算法的稳定性下降，这也是进一步研究该算法的出发点。其次，本文考虑到高压容器设计中的随机因素，建立了高压容器概率优化模型，并采用HPSDE 算法对高压容器的确定型模型与概率模型进行了求解，比较结果表明采用随机模型的计算结果更为合理可靠。