基于贝叶斯更新的滑坡时间概率预测方法

2024-01-22林毓华蔡杏珍陈铭熙

中国煤炭地质 2023年12期

韦成，林毓华，韦宁，江杰，蔡杏珍，陈铭熙

（1.广西工业设计集团有限公司，广西南宁 530020； 2.广西大学土木建筑工程学院，广西南宁 530004）

0 引言

滑坡是我国主要的地质灾害形式，每年造成巨大的生命财产损失，因此，如何准确地预测滑坡时间成为滑坡灾害防治的重要任务之一［1-3］。自1961年SAITO 和UEZAWA 提出第一个实用的滑坡时间预测模型以来，国内外学者已经提出了大量经验或半经验预测模型用于滑坡时间预测［4］。FUKUZONO基于室内降雨滑坡模型试验研究，发现滑坡在加速变形阶段的加速度与速度存在普适性经验关系：v=Avα，其中A 和α 为常数，并对该式积分提出了著名的逆速度法（INV）［5］。VOIGHT 对FUKUZONO 的理论进行数学推广，建立了表征材料破坏出现自加速行为的广义定律［6］。李天斌和陈明东认为典型的滑坡位移-时间曲线与Verhulst 函数的反函数曲线形态类似，提出采用Verhulst 反函数模型对滑坡时间进行预测并验证了模型的有效性［7］。MUFUNDIRWA 等在对FUKUI 预测模型研究的基础上，提出了可以不考虑滑坡破坏机制、岩性和任何其他参数的斜率法（SLO）［8-9］。虽然提出的预测模型众多，但由于受滑坡演化非线性特征、监测误差、环境噪音以及预测模型固有局限性等多种因素的影响，准确预测滑坡的发生时间仍是世界难题［10-12］。近年来，一些学者逐渐关注到滑坡预测存在的不确定性问题，采用区间预测、概率预测等方法对滑坡时间进行不确定性估计［13-14］。例如，采用移动平均法对监测数据进行处理，提出了“破坏时间窗口”的区间预测方法对滑坡时间可能发生的时间段进行估计［13］；ZHANG 等同时考虑观测不确性和模型不确定性对预测的影响，采用逆速度法结合极大似然估计对滑坡时间进行概率预测，获取滑坡最可能发生时刻和时间段［14］。贝叶斯理论作为一种概率反分析的重要手段，广泛应用于岩土体的参数估计、变形预测及灾害预警中［15-17］，但应用于滑坡时间概率预测的研究较少。ZHANG 等采用贝叶斯机器学习方法对滑坡时间进行概率预测，但未量化实时预测的性能。当前，在量化滑坡预测不确定性方面取得了一定的进展，但是考虑滑坡实时预测过程不确定性方面的研究依然有限，更多的是利用最后一次观测获取的数据对滑坡时间进行事后分析［18］。另外，采用贝叶斯理论进行滑坡时间预测的研究正处于起步阶段。

本文的目的是提出一种基于贝叶斯更新并结合多种预测模型的滑坡时间概率预测方法，对实时预测存在的不确定性进行量化并进行预测决策。首先，选用逆速度法、FUKUI 模型和斜率法三种模型用于滑坡时间预测。其次，基于贝叶斯理论建立了三种预测模型的不确定性预测框架，并采用两个滑坡案例验证提出方法的可行性。最后，提出多模型预测决策的建议。

1 滑坡时间预测模型

1.1 逆速度法(INV)

逆速度法是由福囿辉旗基于室内降雨滑坡模型试验研究的基础上提出的，主要用于滑坡加速变形阶段的滑坡时间预测［5］。该假定滑坡破坏时速度无限，则速度倒数1/v趋于0 对应的时刻即为滑坡时间tf，预测模型表达式：

式中：t为观测时间。模型预测曲线1/v-t曲线见图1a。研究表明，α值大多为1.5～2.2，预测曲线近似为直线［5］，因此实际预测中常假定α=2，模型变换为直线型逆速度法（LINV）：

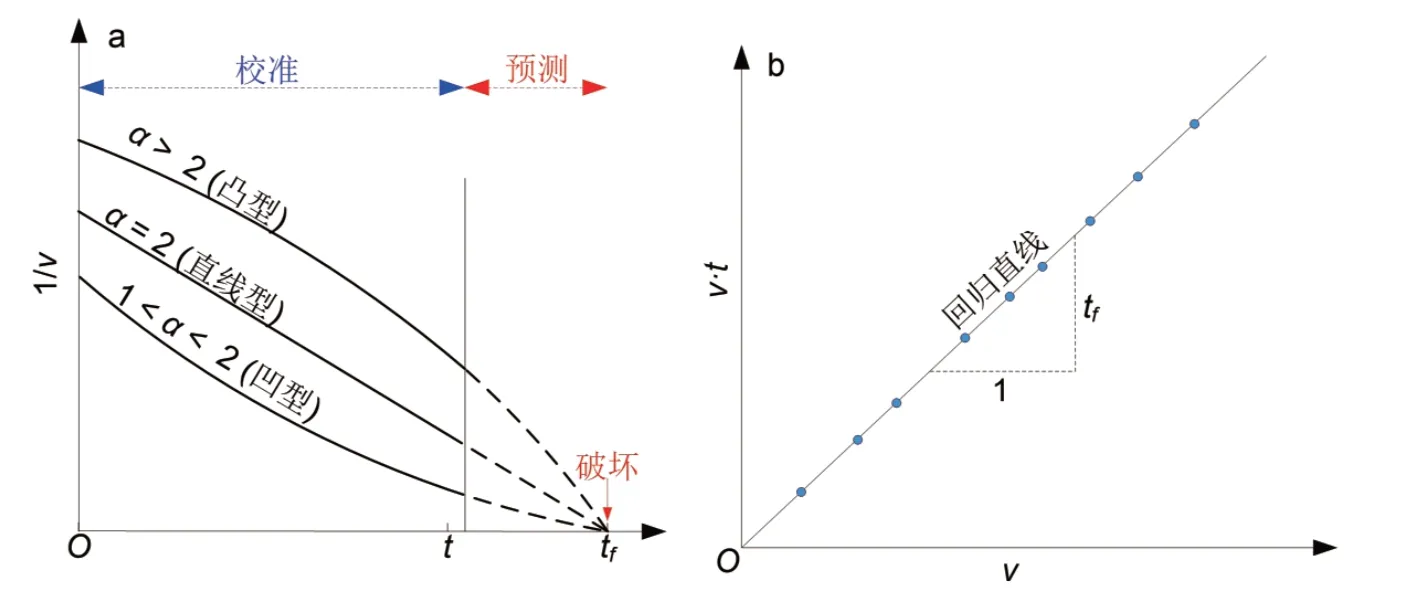
图1 （a）逆速度法和（b）斜率法预测曲线［5，8］Figure 1 （a）Reverse velocity method and（b）slope method for predicting curves［5，8］

1.2 FUKUI预测模型(FM)

FUKUI 等在研究多胡砂岩、水泥砂浆、秋芳大理石等材料单轴压缩试验的蠕变特性时发现这些材料在临近破坏时应变ε 与剩余寿命(tf-t) 的对数成线性关系［9］：

式中：a和b为常数。模型在滑坡时间预测的有效性已得到证明［14］，滑坡预测中ε替换成滑坡位移s。同样，FUKUI 预测模型更适用于加速变形阶段的滑坡时间预测。

1.3 斜率法(SLO)

MUFUNDIRWA 等对FUKUI 预测模型（式（3））进行求导并变换可得［8］：

该模型预测曲线是一条直线（图1b），其中速度v与时间t的乘积（vt）为因变量，v为自变量，滑坡时间为斜率，因此该方法被称为斜率法。由于该模型由Fukui 预测模型得出，同样适用于加速变形阶段的滑坡时间预测。

2 贝叶斯更新预测框架与集成预测

2.1 贝叶斯更新方法

贝叶斯理论用于滑坡预测的基本思想为：根据先验知识对预测模型的未知参数假定一个先验分布，而后基于新加入监测数据持续地对模型参数进行更新，更新后参数的分布为后验分布［15］。假设M（θ）为预测模型，θ为模型参数向量，D=［d1，d2，…，dk］为监测数据的向量。预测模型和监测数据二者关系如下：

式中：εr为预测误差。基于贝叶斯理论，随机变量θ的后验分布p（θ|D）可更新为

式中：p（D|θ）为似然函数；p（θ）为先验分布；p（D）为归一化因子。p（D）可表示为

假定预测误差相互独立且服从正态分布，则似然函数可写成

式中：σε为预测误差的标准差。

2.2 预测模型先验分布确定与后验分布求解方法

模型LINV 的参数向量由A、tf和σε三个参数组成，即θ=｛A，tf，σε｝。在加速变形阶段，模型中的A大于0，且据统计显示A值大小大多不超过80［10，19］。A的具体分布未知，可以采用均匀分布作为先验分布，均匀分布可取大于80 的数值A∞，则A～U（0，A∞）。tf的先验分布同样可以采用均匀分布表示。滑坡进入加速变形阶段，历时一般不会太长，大多数情况小于300 d，因此tf的先验分布可表示为tf～U（tp，tf∞），其中tp，为当前观测时间，tf∞为大于300 d的数值。σε采用正态分布作为先验分布，均值和标准差分别取0 和1，即σε～N（0，1）。对于模型FM 和SLO，tf和σε的先验分布与LINV 的一致。模型FM的a和b在加速变形阶段均为大于0，二者分布未知，因此它们的先验分布同样假定为均匀分布，即a～U（0，a∞）和b～U（0，b∞），其中a∞和b∞为相对较大的数值，与监测位移的量级相关，a∞和b∞一般可取位移值的2～3 倍。后验分布采用No-U-Turn Sampler（NUTS）算法进行求解。NUTS 是由HOFFMAN 和GELMAN 提出的一种改进汉密尔顿蒙特卡罗算法。NUTS 引入“Build binary tree”技术，可动态自适应设置迭代次数和步长，而不需要人工干预，大大提升了收敛速度［20］。NUTS 可通过Python 语言的软件库Pymc3进行调用。

2.3 集成预测与预测决策步骤

滑坡时间预测步骤如下：

1）步骤1。预测模型确定和初始监测数据准备。预测模型采用LINV、SLO 和FM。监测数据采用三个案例加速变形阶段的监测数据，初始预测序列为加速阶段前4 个位移数据点或前三个速度数据点。

2）步骤2。假定模型参数为不确定变量，并确定模型参数的先验分布。

3）步骤3。采用式（8）定义各预测模型的似然函数。

4）步骤4。使用NUTS 算法对各模型参数的后验分布进行采样。NUTS 进行单链MCMC 仿真，样本数为2 000。依据每次加入的最新监测数据获取新的后验分布，并保留每次获取后验分布的样本。预测值均值与真实值的误差采用残差绝对值E表示：

5）步骤5。三个预测模型每次更新后验分布的样本叠加，形成新的后验分布。

6）步骤6。对预测结果进行决策。

3 实例分析

3.1 天荒坪抽水蓄能电站开关站滑坡

该滑坡地处浙江省湖州市安吉县，水电站下水库左岸进水口之上、上下库连接公路之下［21］。坡体由花岗斑岩和含砾流纹质熔凝灰岩组成。1996年3月10 日，受开挖、爆破、降雨等因素的作用，坡体发生整体失稳滑动，体积约为6.2 万m3。这里选取裂缝计J4 的位移时间序列进行分析（图2）。本案例以1996 年2 月1 作为加速起点，并令加速起点时间t0=1 d，则真实滑坡时间Tf=28 d。

图2 天荒坪抽水蓄能电站开关站滑坡的累积位移时间序列Figure 2 Accumulated displacement time series of landslide in Tianhuangping pumped storage power station

表1 和图3 为模型LINV、SLO、FM 以及三模型集成最后一次观测的预测结果和概率分布图。在单一模型预测中，模型LINV 和FM 的采样区间和95%置信区间（CI）将真实滑坡时间Tf包含其中，而SLO预测滑坡时间的采样区间和95%置信区间均早于Tf。LINV 的预测均值（tf= 29.26 d）晚于Tf，FM（tf= 27.38 d）和SLO（tf=26.27d）的预测均值略早于Tf。LINV 的预测标准差（5.78 d）远大于另外两个模型（0.39 d），表明LINV 受模型本身的误差和监测数噪音的影响较大，预测具有明显不确定性。各模型预测最可能的滑坡时间（即最大后验估计值）均早于Tf，但总体上与预测均值的差异不大。三个预测模型集成的预测结果显示其整合的采样区间和95%置信区间均将Tf包含其中。最可能发生滑坡的预测时间为26.85 d，早于Tf。集成模型的预测均值（tf= 27.64 d）比三个单一模型的预测均值更接近Tf。

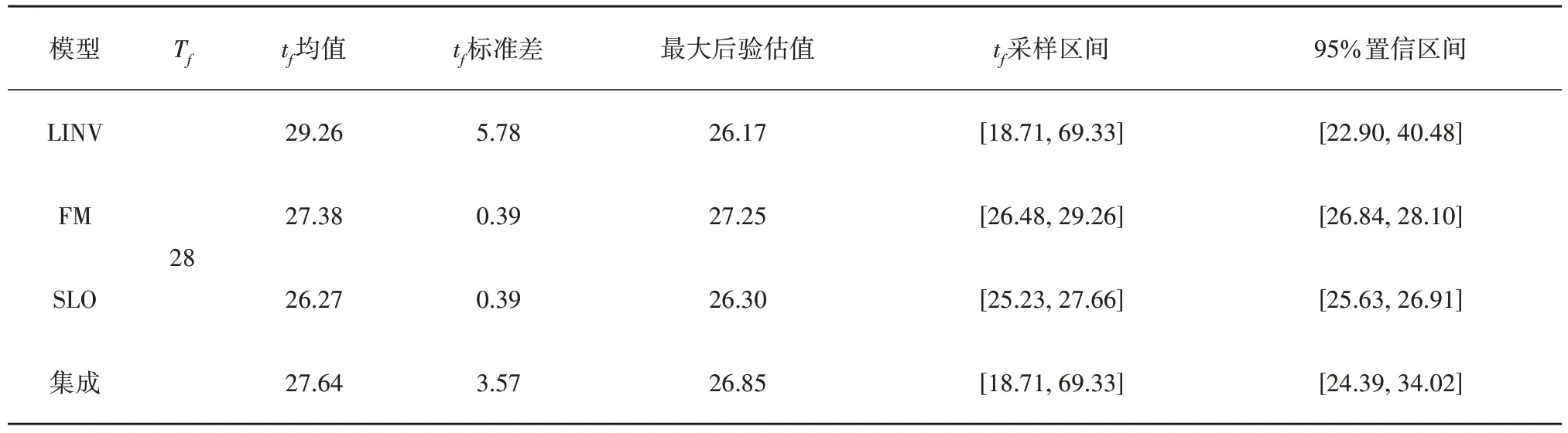
表1 最后一次观测的滑坡时间预测结果Table 1 Prediction results of the last observation landslide time

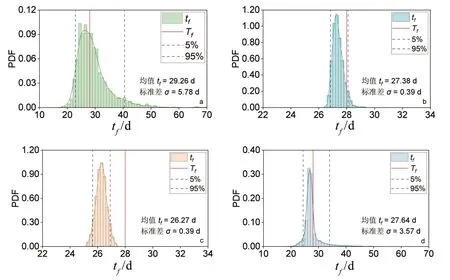
图3 最后一次观测滑坡时间预测结果：（a）LINV；（b）FM；（c）SLO；（d）模型集成Figure 3 Prediction results of the last observation landslide time：（a）LINV；（b）FM；（c）SLO；（d）model integration

由图4、图5 可看出，无论是单一预测模型还是集成预测，在初始加速阶段，95%置信区间相对较宽，表明预测具有明显的不确定性，滑坡的破坏趋势仍很模糊，不可能获得可靠的预测；在临滑阶段，置信区间变窄或宽度变化趋于稳定，表明滑坡破坏趋势变得清晰，可获得相对可靠的预测结果。与另外两个单一预测模型相比，LINV预测的置信区宽度较大，代表预测不确定性非常强，但在预测的时间尺度内均将Tf容纳其中。三个模型集成的预测结果，降低了LINV 预测的不确定性，并且在t=14 d之后将Tf包含其中。各模型预测的残差绝对值也基本随时间的增长而呈减小趋势，其中集合预测的残差绝对值的大小介于其它三个模型残差绝对值之间，且演化趋势较为平稳。

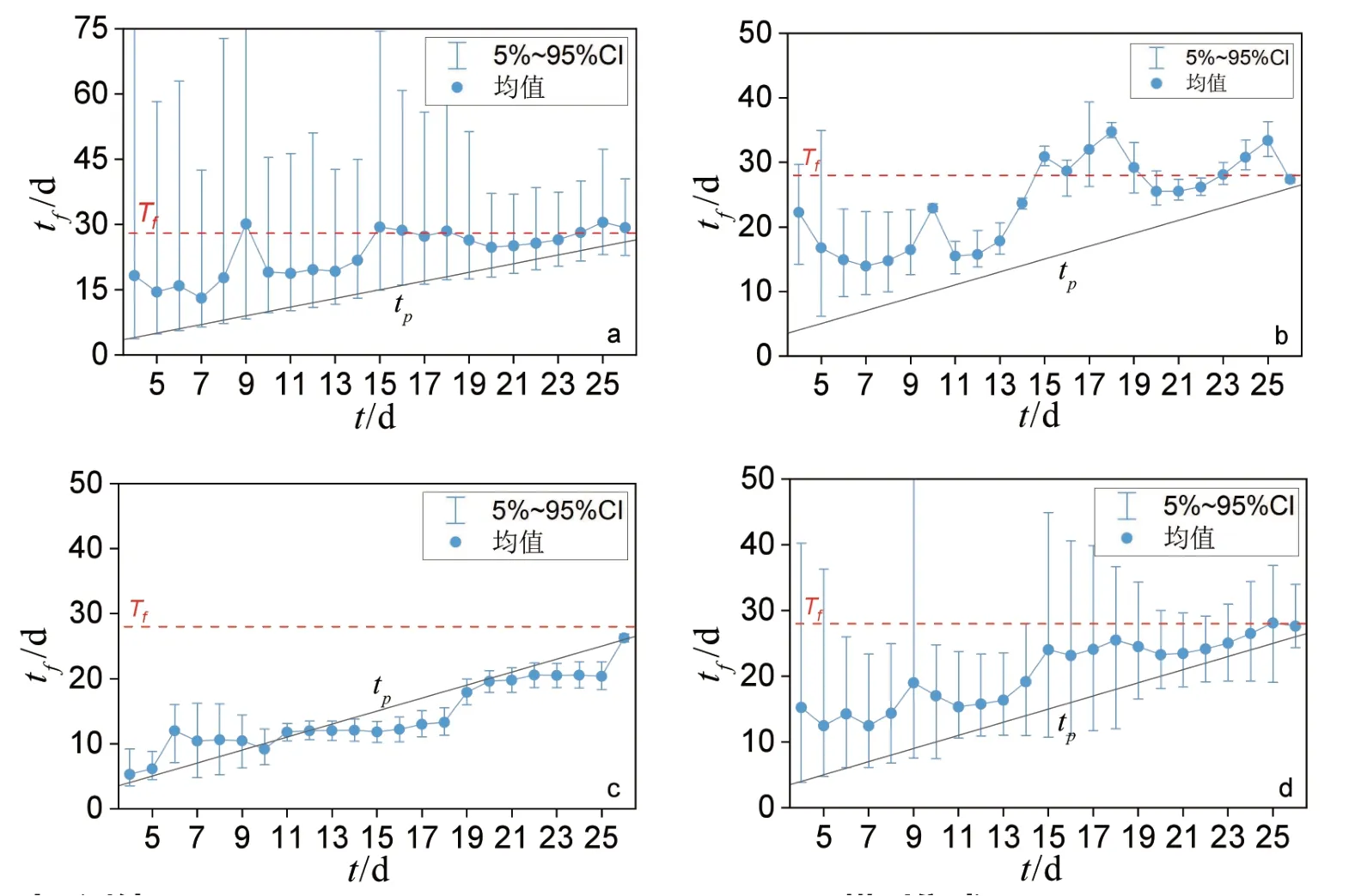
图4 实时预测结果：（a）LINV；（b）FM；（c）SLO；（d）模型集成Figure 4 Real-time prediction results：（a）LINV；（b）FM；（c）SLO；（d）model integration

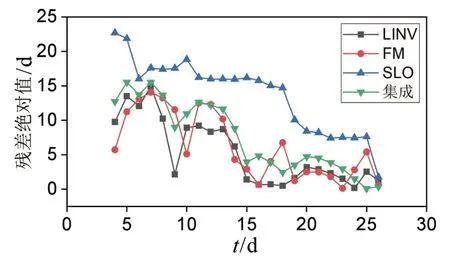
图5 开关站滑坡的滑坡时间预测值与观测值的残差绝对值Figure 5 Absolute residual value between predicted and observed landslide time of switch station

单一模型和模型集成的预测在前期加速变形阶段同样表现出明显的不确定性，但在t= 80.01 d之后预测的置信区间变得非常窄，并且Tf基本位于模型集成预测的置信区间之内，代表破坏趋势已经非常明显，可对滑坡时间进行可靠的预测。

3.2 准格尔旗某露天煤矿滑坡

该滑坡案例来源于内蒙古自治区鄂尔多斯市准格尔旗的某露天煤矿［22］，于2020 年1 月4 日早上发生滑坡事件。滑坡变形破坏的累积位移时间序列见图6。根据原文献提供的数据，初始位移的相对时间为1.08 h，滑坡从t=60.09 h 开始加速，真实滑坡时间Tf为94.23 h。

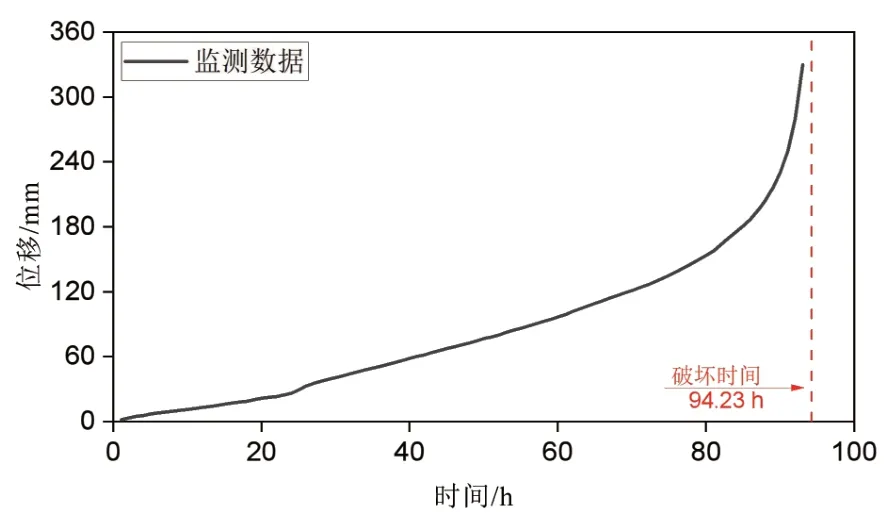
图6 准格尔旗某露天煤矿滑坡的累积位移时间序列Figure 6 Accumulated displacement time series of landslide in an opencast coal mine in Zhungeer

表2和图7为模型LINV、SLO、FM以及三模型集成最后一次观测的预测结果和概率分布图。在单一模型预测中，Tf位于模型LINV 和SLO 的采样区间之内，但只有SLO 的95%置信区间能包含Tf。LINV 预测的置信区间晚于Tf，而FM 预测的置信区早于Tf。然而，三个模型最后一次观测的预测均值均非常接近于Tf，误差在2 h以内。与上一案例相同，LINV 的预测标准差是三个模型最大的。最大后验估计值与Tf接近。模型集成的预测置信区间将容纳其中，最大后验估计值略早于Tf。集成的预测结果在一定程度上降低了单个预测模型带来的不可靠性。

表2 最后一次观测的滑坡时间预测结果Table 2 Prediction results of the last observation landslide time

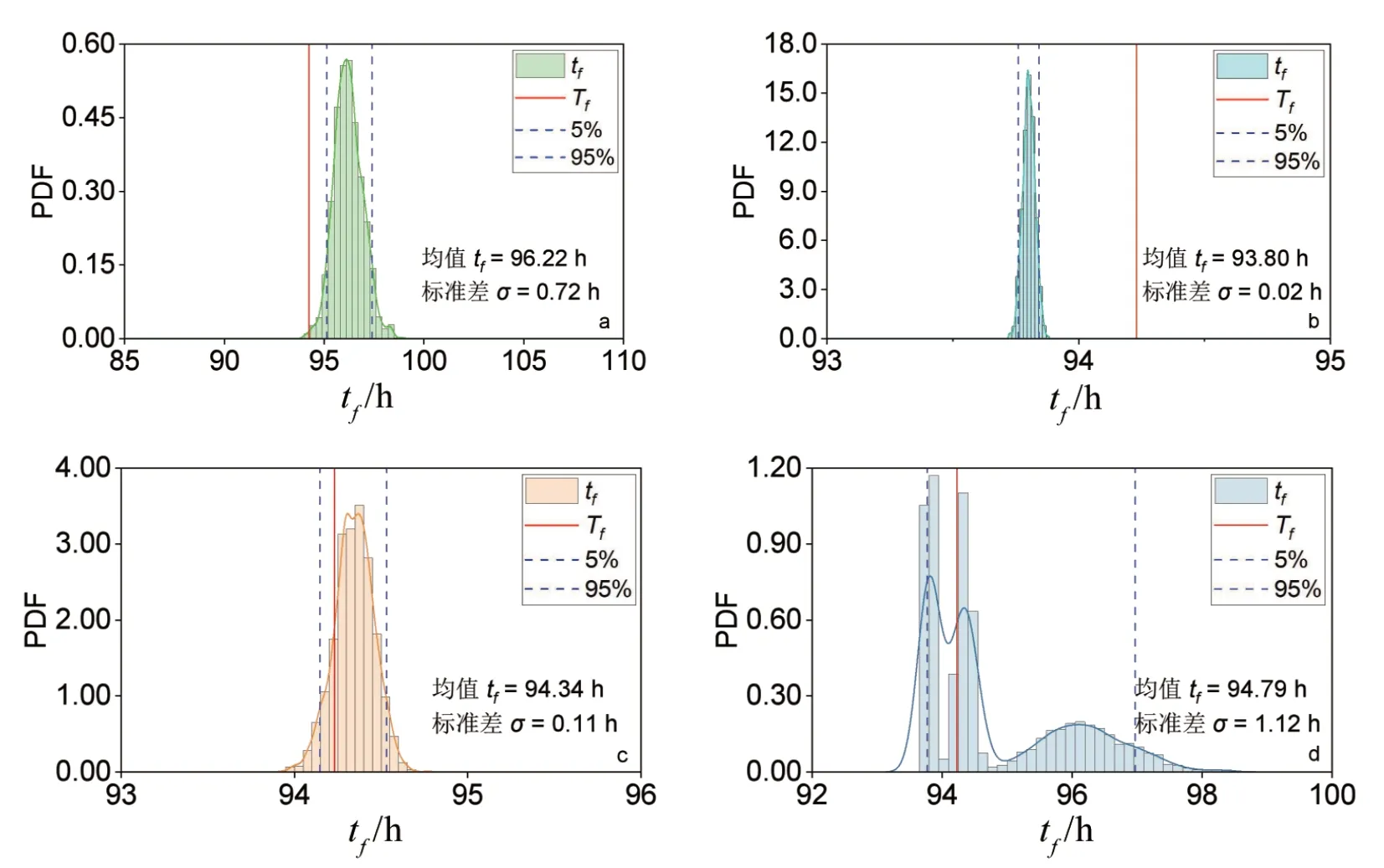
图7 最后一次观测滑坡时间预测结果：（a）LINV；（b）FM；（c）SLO；（d）模型集成Figure 7 Prediction results of the last observation landslide time：（a）LINV；（b）FM；（c）SLO；（d）model integration

图8为实时预测结果，图9为预测均值与真实滑坡时间的残差值。结果显示，单一模型和模型集成的预测在前期加速变形阶段同样表现出明显的不确定性，但在t= 80.01 d 之后预测的置信区间变得非常窄，并且Tf基本位于模型集成预测的置信区间之内，代表破坏趋势已经非常明显，可对滑坡时间进行可靠的预测。与前一个案例类似，该案例预测的残差绝对值同样表现为E随时间的增长而呈减小趋势，其中集合预测的残差绝对值的大小介于其它三个模型残差绝对值之间，且演化趋势较为平稳。

图8 实时预测结果：（a）LINV；（b）FM；（c）SLO；（d）模型集成Figure 8 Real-time prediction results：（a）LINV；（b）FM；（c）SLO；（d）model integration

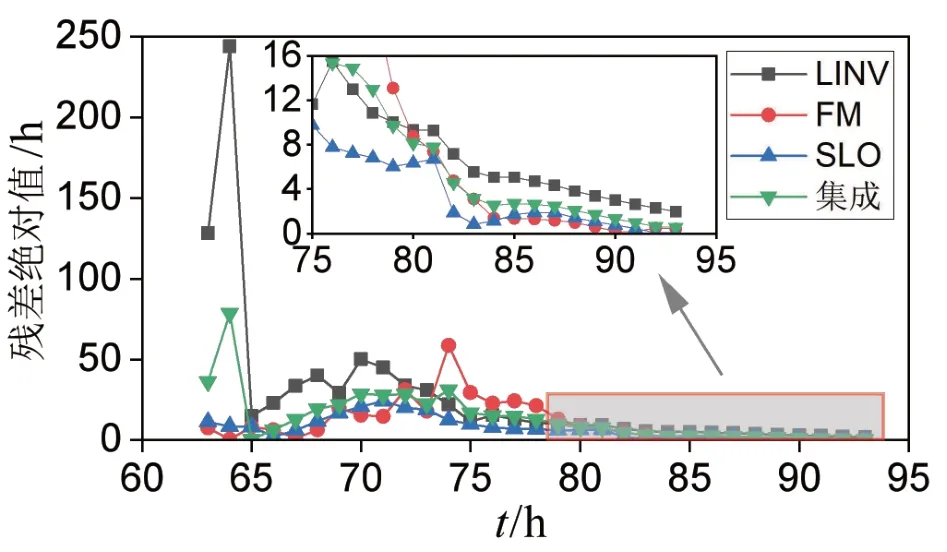
图9 某露天煤矿滑坡的滑坡时间预测值与观测值的残差绝对值Figure 9 Absolute residual value between predicted and observed landslide time in an opencast coal mine

4 讨论

由上述预测分析可知，利用滑坡加速变形阶段的观测数据预测滑坡时间具有如下规律：在加速变形阶段前期，各模型的预测均值和最大后验估计值明显偏离Tf，预测的置信区间跨度相对较宽，预测具有明显的不确定性；在滑坡进入临滑阶段后，各模型的预测均值和最大后验估计值向Tf收敛并在其附近波动，预测的置信区间宽度收缩或趋于稳定。因此，在滑坡时间预测时，需判识滑坡所处的演化阶段。许强等将滑坡演化的加速变形阶段划分为初加速、中加速和临滑加速三个阶段［23］。两个案例的预测结果表明，在中加速变形阶段，滑坡时间预测值开始向真实值收敛；进入临滑阶段后，各模型预测出滑坡时间相对可靠。

在三个模型的预测中，根据预测的残差绝对值E的动态演化规律，在两个滑坡中FM 模型的E的值均相对较小，而LINV模型和SLO模型变化较大。总体而言，LINV模型在天荒坪抽水蓄能电站开关站滑坡的预测分析中E是三个模型中最小的，而在准格尔旗某露天煤矿滑坡中的E是三个模型中最大的；而SLO 模型的情况恰好相反。这些模型的预测能力需要更多的滑坡案例进行分析，以确定滑坡时间预测的最佳模型。虽然采用贝叶斯更新方法量化了预测不确定性，但是模型本身的预测性能仍对预测结果占主控作用。另外，集成预测的E基本位于三个单一模型预测的E之间，其演化相对平稳，且其值大小处于一个相对较低的水平。因此，采用各模型预测结果的集成并进行综合评价对滑坡时间进行分析是极为关键的。

针对上述分析，本研究对滑坡预测决策提出如下建议：

1）对比多模型预测的滑坡时间均值或最大后验估计值。在两个案例中，二者之间的差距相对较小，可取二者之一或平均值为确定性预测结果。当多时刻、多模型的预测均值或最大后验估计值在某一固定值附近波动，可认为获得较为可靠预测结果。

2）预测的95%置信区间作为滑坡时间窗口。窗口越宽或者随时间波动性越大，代表预测不确定越高，边坡破坏的可能性仍相对较低。窗口越窄或者随时间波动性降低，可认为当前观测数据已经能较为清晰地反映滑坡的破坏趋势，预测结果较为可靠。不同案例的时间窗口的宽度与变形特征、观测噪音等因素相关，很难确定一个固定的阈值窗口，因此这窗口的宽窄是相对不同预测时刻而言的。此外，集成预测模型95%置信区间的下限值可为一个临界预警阈值。