研究教材习题 破解历年真题——以2019年人教A版教材必修第一册58页第5题为例

郭天总 马静辉 王红波

(河北省邯郸市永年区第二中学)

教材是教师教学、学生学习及备战高考的最重要的资料,因为高考试题命制的一个原则是“源于课本,但高于课本”,所以高考命题很注重开发教材、研究教材,挖掘教材知识的考查价值和功能,许多高考试题所涉及的思想方法都源于对教材例、习题的深入研究.因此,在平时的教学与备考中要充分发挥教材的功能,从烦琐的复习资料中跳出来,研读教材,吸取营养,更好地培养学生的数学核心素养.下面作者就自己在研究教材、寻找通性通法、破解高考真题时的一些做法与大家分享、交流,希望能起到抛砖引玉的作用.

一、经典习题

(2019年人教A版必修第一册58页第5题)若a,b>0,且ab=a+b+3,求ab的范围.

【分析】看问题:求ab的范围.(属于范围问题)

想方法:(1)不等式思想;(2)函数思想;(3)数形结合思想;

看条件:a,b>0,ab=a+b+3;

定措施:

措施一:令ab=t(t>0),与ab=a+b+3联立建立关于b(或a)的一元二次方程,根据方程有正根建立关于t的不等式求解.

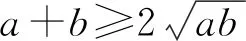
【解析】法一:由已知得a+b=ab-3,

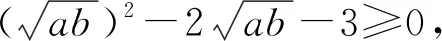
换元

代入ab=a+b+3,

整理得b2+(3-t)b+t=0,

联立

因为该方程有正根,

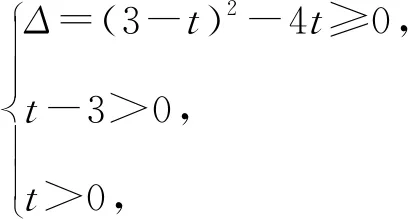
列式

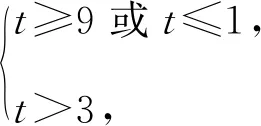
求解

所以ab的范围为[9,+∞).

二、方法梳理

虽然上述习题可用三种方法来解决,但这三种方法中,法一、法二是常用的通性通法.通过对法二的解题过程进行梳理,可以总结出这种方法的基本步骤为:换元、联立、列式、求解.其中的换元即把所求的g(a,b)看成一个整体t,联立是把g(a,b)=t与题设中已知的等量关系联立之后,构造一个一元二次方程,列式是根据方程有根(或有正根),列出关于t的不等式,通过解不等式达到求范围的目的.这样的归纳总结,可以培养学生的程序性思维,提高学生分析问题和解决问题的能力,提高学生的逻辑推理素养.

教师在教学中若能更多地注重“多题归一”(所谓“一”就是具有普遍意义和广泛迁移性的、“含金量”较高的解题方法与策略),更多地注重思考题目的“核心”是什么,从题目中“提炼”反映数学本质的东西,掌握好解决数学基本问题的通性通法,这样才能达到学生会一道,通一片的教学目的,起到事半功倍的教学效果.

三、破解真题

“2019年人教A版必修第一册58页第5题:若a,b>0,且ab=a+b+3,求ab的范围.”这是一道双变量的求范围问题,此题既可配凑出定值利用基本不等式或其变形求解,也可通过换元法,转化为一元二次方程根的分布来求解.本习题中的条件ab=a+b+3是个很好的情景,该情景可以通过圆、解三角形、椭圆等知识点来呈现,因此以此题为依据扩展出来的高考题目有很多,列举如下:

【真题1】[2023年高考全国乙卷数学(文)第11题]已知实数x,y满足x2+y2-4x-2y-4=0,则x-y的最大值是

( )

【答案】C

【解析】法一:令x-y=t,则x=t+y,

换元

代入原式化简得

2y2+(2t-6)y+t2-4t-4=0,

联立

因为存在实数y,则Δ≥0,

即(2t-6)2-4×2(t2-4t-4)≥0,

列式

化简得t2-2t-17≤0,

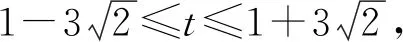
求解

法二:由a2+b2≥2ab(a,b∈R)得

由已知得(x-2)2+(y-1)2=9,

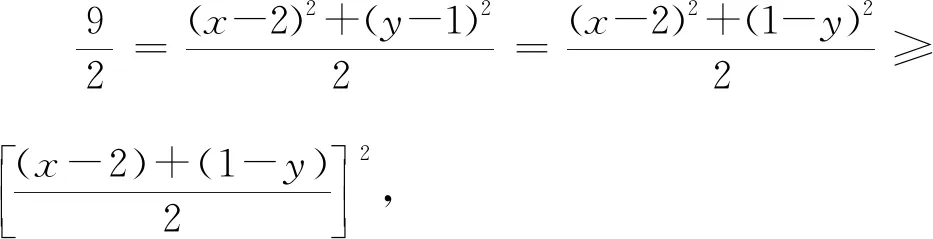
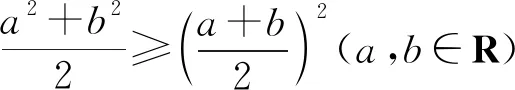
【真题2】(2022·新高考Ⅱ卷第12题)(多选题)对任意x,y,x2+y2-xy=1,则

( )

A.x+y≤1 B.x+y≥-2

C.x2+y2≤2 D.x2+y2≥1

【答案】BC

所以x2+y2≤2,当且仅当x=y=±1时等号成立,故C对.

由已知得x2+y2-xy=(x+y)2-3xy=1,

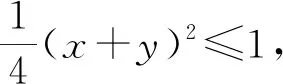
所以-2≤x+y≤2,故B对.

法二:令x+y=t,则y=t-x,

换元

代入x2+y2-xy=1,

可得x2+(t-x)2-x(t-x)=1,

联立

整理得3x2-3tx+t2-1=0.

因为该方程有根,

所以Δ=9t2-4×3×(t2-1)≥0,

列式

解得-2≤t≤2,即-2≤x+y≤2.

求解

令x2+y2=t(t>0),则t-xy=1,

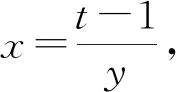
换元

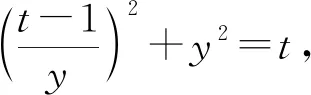
整理得y4-ty2+(t-1)2=0,

联立

因为该方程有根,

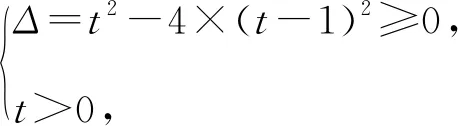
列式

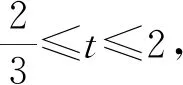
求解

【方法点评】由已知条件x2+y2-xy=1及问题的结构特征,该题首先容易想到的是法一,即利用基本不等式及其变形求解.法二是利用换元法构造一元二次方程,然后再用判别式建立不等式去x+y,x2+y2的范围.对比法一、法二可知,法一的计算量、思维量要比法二要小,是解决本题的最优解法.所以在平时的教学中,对于典型的习题要注意归纳总结各种不同的解法,并熟练掌握处理此类问题的通性通法,但在掌握基本方法的同时,要学会分析、比较,在会做的基础之上寻找解决问题的最优解法,唯有如此,当学生遇到不同问题时,才会选择恰当的方法,解题时少走弯路.

( )

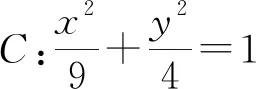
A.13 B.12 C.9 D.6

【答案】C

【详解】法一:由椭圆的定义知

|MF1|+|MF2|=2a=6,

所以|MF1||MF2|≤9,当且仅当|MF1|=|MF2|=3时等号成立,

则|MF1|·|MF2|的最大值为9.

法二:设|MF1|·|MF2|=t(t>0),

换元

由已知得a2=9,b2=4,

则|MF1|+|MF2|=2a=6 ①,

|MF2|2-6|MF2|+t=0,

联立

因为该方程有正根,

又t>0,所以Δ=62-4×t≥0,

列式

解得t≤9,则|MF1|·|MF2|的最大值为9.

求解

【真题4】(2020年高考数学课标Ⅱ卷理科)△ABC中,sin2A-sin2B-sin2C=sinBsinC.

(1)求A;(2)若BC=3,求△ABC周长的最大值.

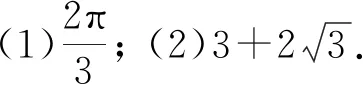
【解析】(1)由正弦定理可得

BC2-AC2-AB2=AC·AB,

(2)法一:由(1)及余弦定理知AC2+AB2+AC·AB=9,即(AC+AB)2-AC·AB=9,

由基本不等式得

即4(AC+AB)2-36≤(AB+AC)2,

整理得(AC+AB)2≤12,

又AC+AB>3,

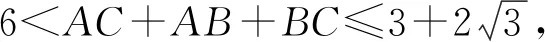
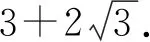
法二:令AC+AB=t(t>0),

则AC=t-AB,

换元

由(1)及余弦定理得BC2=AC2+AB2-2AC·ABcosA=AC2+AB2+AC·AB=9,

即(AC+AB)2-AC·AB=9 ①.

把AC=t-AB代入①式整理得

AB2-t·AB+t2-9=0,

联立

列式

求解

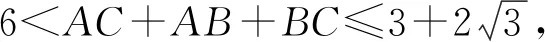
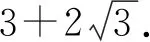
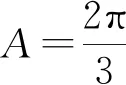
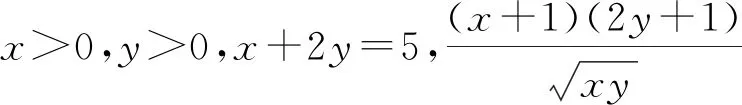
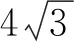
【解析】法一:因为x>0,y>0,x+2y=5,

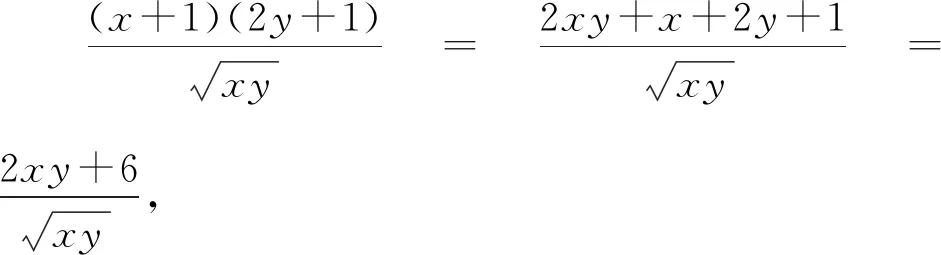
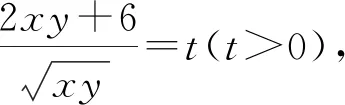
换元

因为该方程有正根,

构造

列式

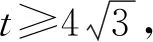
求解

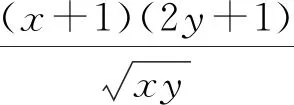
【真题6】[2018年高考数学课标Ⅲ卷(理)6题]直线x+y+2=0分别与x轴、y轴交于A,B两点,点P在圆(x-2)2+y2=2上,则△ABP面积的取值范围是

( )

A.[2,6] B.[4,8]

【答案】A

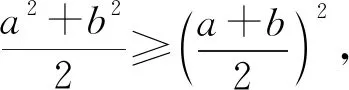
整理得|x-2+y|≤2,∴0≤x+y≤4,

则2≤x+y+2≤6,

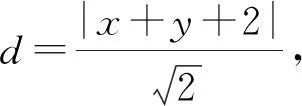
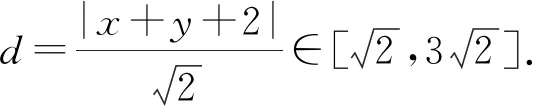
∴S△PAB∈[2,6].

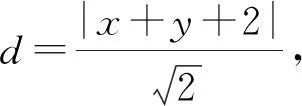
令t=x+y+2 ①,

换元

则①代入圆的方程整理得

2x2-2tx+t2-4t+6=0,

联立

根据题意该方程有解,则有

Δ=4t2-4×2×(t2-4t+6)≥0,

列式

解得2≤t≤6,

求解

∴S△PAB∈[2,6].

【试题点评】

1.从时间和形式上来说,以上六道真题,从2018年到2023年,时间跨度为六年,形式上从老高考到新高考,试题的呈现形式年年不同,但考查的数学思想是不变的,用的是一种数学方法,即不等式方法,这充分体现了高考试题标新不立异,立异不偏离,常考常新,年年创新的特点.

2.从命题情境角度来说,以上六道真题是毫不相干的题目,分别考查了二元二次方程、椭圆、解三角形、直线与圆等相关的知识.但是从方法二的角度来说,相同的都是一种解题模式,即换元、联立、列式、求解.充分体现了高考试题对于同一考点可以变换角度与变换题型再考,也就是说同样的情境,今年这样问,明年那样问.

3.从方法的优越性来说,上述解析中的法一与法二孰优孰劣是相对于问题而言的,比如对于【2023年高考全国乙卷数学(文)第11题】来说,利用换元法构造不等式就比使用基本不等式简便,但对于【2021·新高考Ⅰ卷第5题】来说,利用基本不等式就比换元法构造不等式简便.因此平时的教学中,在会做的基础之上,指导学生去寻找最优的解题方法,因为高考是选拔性考试,只有保证每道试题用的都是最优的解题方法,才能缩短解题时间,才有可能取得优异成绩.

四、教学启示

以上六道年份不一样、情境不一样的高考真题,解题方法最终归根到底都回归到课本上的2019年人教A版必修第一册58页第5题,真正做到了万变不离其宗,而以这种思想可以解决的多元范围问题在历届高考中频频“出镜”.具体如下表所示:

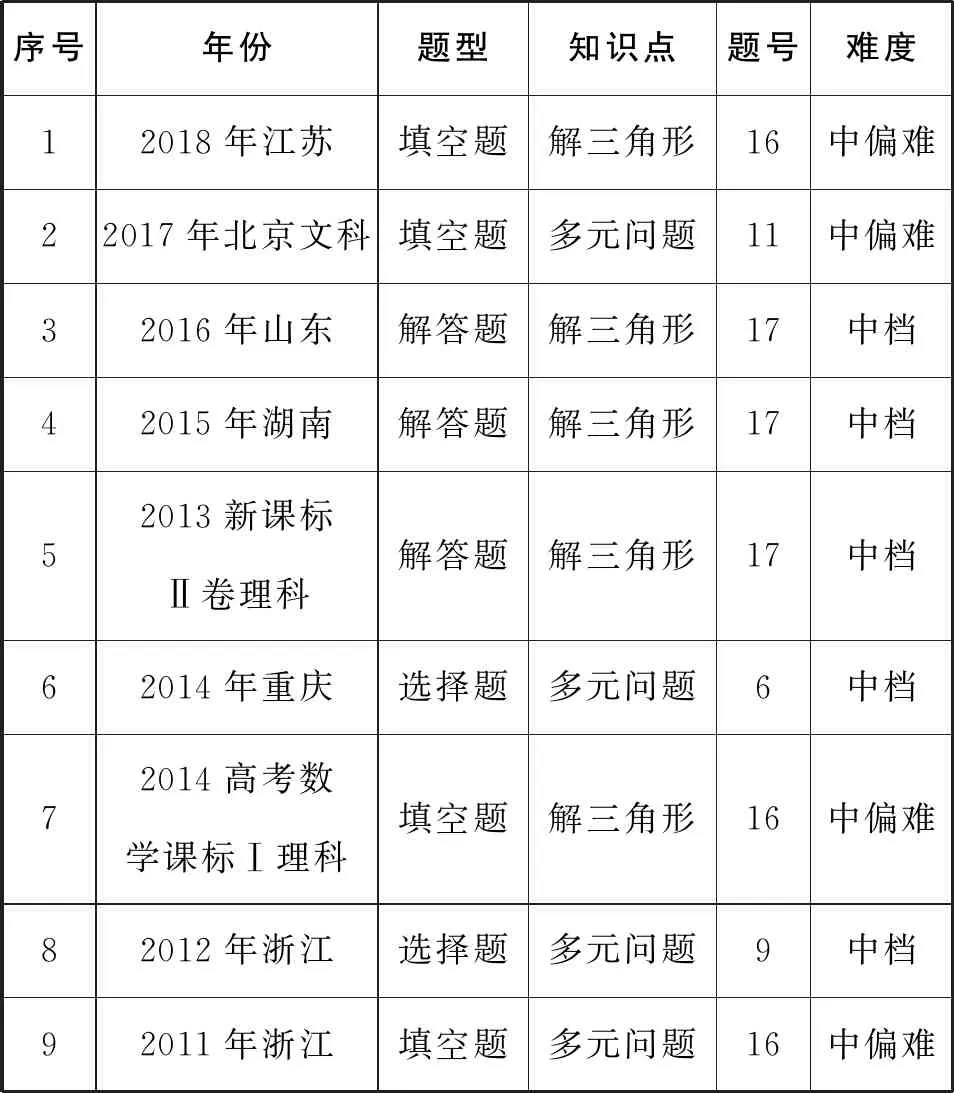
序号年份题型知识点题号难度12018年江苏填空题解三角形16中偏难22017年北京文科填空题多元问题11中偏难32016年山东解答题解三角形17中档42015年湖南解答题解三角形17中档52013新课标Ⅱ卷理科解答题解三角形17中档62014年重庆选择题多元问题6中档72014高考数学课标Ⅰ理科填空题解三角形16中偏难82012年浙江选择题多元问题9中档92011年浙江填空题多元问题16中偏难

事实胜于雄辩,一道道高考真题告诉我们,高考试卷题目是立足于课本,根据课本上的题目加以扩展而来的.教材中的例题、习题是基础,是根本,是非常重要的.因此在高考数学的备考中,教师和学生都要过课本上的例题关、习题关.教材中的每一道例题、习题都要研究透彻,掌握它的通性通法,掌握它的知识内涵.研究教材,深入挖掘可以作为知识考查载体的题目,深入探讨有拔高潜力的题目,充分发挥例习题的隐藏功能,这样在高中数学的教学中、在高考的备考中少走弯路,能够起到事半功倍的效果.

综上所述,在数学教学中,通性通法的使用和深层次的理解伴随一个螺旋上升、逐步深化、直达本质的过程.只有真正重视通性通法,多方位、多侧面地深入理解和系统总结,才能让学生抓住数学问题的本质,将学生的知识学习引向深入的探究,提升学生的数学学科核心素养.