基于改进北方苍鹰优化算法的封闭小区开放决策模型
2024-01-20王连震杜亚北石凌云张国立郑夫水
王连震,杜亚北,石凌云,张国立,郑夫水
(东北林业大学 土木与交通学院,哈尔滨 150000)
封闭式小区在我国城市居民小区模式中占据了主流,大量的小区封闭导致城市路网密度低、交通微循环差,对城市的路网结构造成了破坏,使得城市道路极易发生堵塞。早在2016年,中共中央国务院印发《关于进一步加强城市规划建设管理工作的若干意见》提出了推广街区制,逐步打开住宅小区和单位大院,以期解决路网布局问题,缓解交通阻塞状况和促进土地资源节约利用。封闭小区开放后会使城市的路网密度增加,缓解交通拥堵。目前,许多学者就这一重要议题开展研究分析。
Roitman[1]提出封闭式小区概念,即被围墙包围,将空间私有化并限制他人进入的居住区;Yao等[2]研究开放封闭式社区将使当前道路网络的连通性和可达性增加;Zhang等[3]认为封闭小区越位于城市中心,对路网流量影响就越大;Atkinson等[4]认为封闭小区削弱了城市机动性,加剧社会隔离,不利于城市社会的和谐与融合;Ehwi[5]研究封闭式社区的用途,认为封闭式社区给公众提供了更好的安全感;El-Ekhteyar等[6]通过对居民的现场访问,得出居民和社区有很多联系,多数居民不赞同小区开放;Kuhlberg等[7]通过调查发现拥有开放街道的美国城市数量正在增加;Dong等[8]利用流量熵模型和模糊均值(FCM)方法,建立一种新的开放评估熵模型,对小区开放选取指标进行评价;Borger等[9]认为从主要道路分流到当地社区的交通带来了不利影响,使居民有强烈的意愿关闭当地小区道路;Feng等[10]综合考虑行人、非机动车等各种网络节点,构建多层复杂网络,对封闭式社区交通容量进行研究,小区开放后交通容量提升;Zhang等[11]将交通出行分为小区内部交通和小区外部交通两部分,然后分析小区大小对不同交通方式的交通性能(如行驶距离、行驶时间和转弯次数)影响。
毛斌菁等[12]分析从封闭小区到开放街区过程中产生的问题以及解决问题的方法;和亮等[13]提出封闭式小区所在的位置、面积、内部和外部道路状况等因素都能对城市路网的交通状态产生影响,封闭式小区想要决定是否开放,需要在进行决策之前对小区与周边道路状况进行系统性评估;王宇晗等[14]认为小区规模的过大造成了交通可达性差、城市路网密度低、长期占用社会公共停车位、公共设施使用效率低;戴宇轩[15]根据Wardrop第一平衡原理对不同内部道路结构的小区在封闭与开放两种情况下进行评估;闫梓昂等[16]通过建立评价体系对小区周边道路通行能力进行评价,分析比较封闭小区开放前后周边路网的运行质量;胡祖平等[17]基于网络可靠性对街区的开放进行适宜度研究;刘馨洁等[18]考虑出行者决策惯性对超级街区开放产生的影响进行分析;霍佳萌[19]提出某小区交通开放路网设计方案,并对小区开放前后路网的交通状况进行评价;张凌煊等[20]结合街区内外部出行,对各种交通方式产生的出行时间和费用在不同街区尺度下的变化特征进行分析;方彬等[21]认为我国街区制的推广应以“开放式、小街区、密路网”为标准,对我国较大的封闭小区进行开放;周雨阳等[22]研究小区出行对就医的影响,对各交通小区的就医出行可达性进行计算。
从上述国内外研究中可以看出,大多数研究者更多地关注了封闭式小区打开之后对城市交通的影响,没有充分考虑到封闭式小区开放后对小区内部的交通安全、环境和噪声的影响。小区居民最关注的是封闭小区开放后,外界车辆进入小区产生的安全问题,此举将降低居民的安全感[23]。同时,随着小区内部道路的对外开放,将产生环境污染和噪声污染问题,这些问题在小区开放后急需治理。此外,已有研究没有考虑小区内部道路连接的出入口道数量对小区内部道路开放的影响,小区内部道路连接的出入口道数量能从一定程度上反映小区位置、内部及外部道路状况,如果入口道数量远高于出口道数量,极易造成堵塞。
基于此,文中综合考虑出行时间和安全隐患、环境污染、噪声污染,同时考虑小区出入口数量的关系,构建封闭小区开放的多目标优化模型。由于该问题是典型的NP-hard问题,文中设计一种增强的北方苍鹰优化算法(ENGO)来求解问题。
1 封闭小区开放的影响因素
考虑交通出行时间、安全、环境、噪声的影响,封闭小区开放前后的出行总费用包含行驶费用、安全事故产生的费用、环境污染治理和噪声污染治理产生的费用。
以封闭小区为研究对象,分析出行时间、交通安全、环境污染、噪声污染与费用的关系,将上述内容根据相应的关系转换为费用值函数。
1.1 行驶费用
车辆在出行过程中,所包含的费用包含出行时间费用和出行本身产生费用之和,其中出行时间费用是根据一天中时间价值最高的早高峰时间价值来计算。
封闭式小区开放前,车辆通过封闭式小区外部道路,其路网行驶费用可表示为
(1)
式中:Ey1为封闭式小区开放前路网行驶费用,元·h-1;Et1为车辆出行产生的费用,元·h-1;Et2为出行者的时间价值,元·h-1;y1为路网中封闭式小区外部所有路段长度,km;ty1为车辆在外部路段y1上的出行时间,h;xy1为路段y1上的车辆交通量,veh·h-1。
封闭小区开放后,需计算小区内部和外部路段上车辆的行驶费用。小区内部路段根据路阻函数计算车辆行驶费用,算式[24]为
(2)
式中:Ey2为封闭式小区开放后路网行驶费用,元·h-1;y2为封闭式小区内部所有路段长度,km;ly2为路段y2的长度,km;Vy2为路段y2上的速度,km·h-1;xy2为路段y2上的交通量,veh·h-1;cy2为路段y2的实际通行能力,veh·h-1。
封闭小区开放后,考虑车辆在内部道路与外部道路通行,车辆的总出行时间费用算式为
Ey=Ey1+Ey2
(3)
式中:Ey为封闭小区开放时路网的总行驶费用,元·h-1。
1.2 安全隐患损失费用
较多研究表明,安全问题是小区内部居民对封闭小区开放担心的重点问题,所以文中将预测发生交通事故造成的可能损失纳入到考虑范围中,其算式为
(4)
式中:ER为安全隐患损失费用,元·h-1;S为平均每起事故造成的财产损失费用,元·h-1。
1.3 环境污染治理费用
封闭小区开放后,小区内部道路交通量增加,汽车尾气排放产生污染,治理环境污染产生的费用算式为
(5)
式中:EFK为第i种污染物系数,根据《道路机动车大气污染物排放清单编制技术指南(试行)》进行取值,计算得EFCO=0.521 6γCO,EFHC=0.063 4γHC,EFNOx=0.019 8γNOx,其中γCO、γHC和γNOx为速度修正因子,参照表1[25]取值。
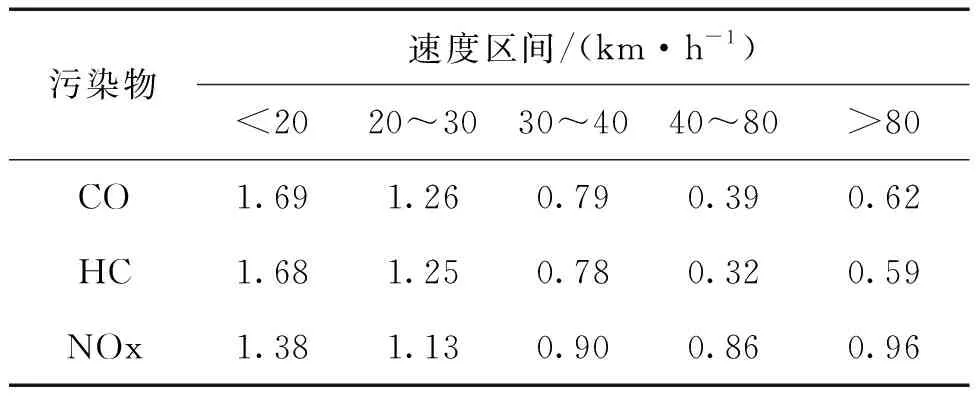
表1 小型汽车速度修正因子取值对照
1.4 噪声污染治理费用
封闭小区开放后,通过的车辆会产生噪声,交通噪声污染会带来各种问题,影响小区内居民的身体健康,影响楼房的销售等。现实生活中,控制噪声污染会产生一定费用。车辆产生的交通噪声与费用的关系算式[26]为
Eleq=1.25a(9.24lgxy2-17.829lgVy2+
70.073+Leqm)b
(6)
式中:Eleq为交通噪声治理费用,元·h-1;leq为车辆通过小区内部道路产生的噪声,dB;Leqm为标准环境噪声,dB。
2 封闭小区开放决策模型
2.1 开放决策方式
1)封闭小区内部道路是否开放决策。1和0表示封闭小区是否开放,1表示开放,0表示不开放。
2)封闭小区内部道路单双行决策。封闭小区内部1条道路包含2个方向的路段,即两个0~1决策变量的组合,决策为11表示两个方向的路段均开放,决策为00表示小区内部两个方向均不开放,决策为01、10表示只开放一个方向的路段。
2.2 模型建立
所建立的多目标优化模型中,一个目标函数是以广义费用值最小为目标,另一个目标函数是以考虑小区开放最大为目标。
2.2.1 费用值函数
费用值函数算式为
ω2ER+ω3EQ+ω4ELeq)]}
(7)
式中:Et为费用值函数;δ为0~1决策变量,1为开放,0为不开放;ω1、ω2、ω3、ω4分别为行驶费用、安全隐患损失费用、噪声污染治理费用和环境污染治理费用的目标权重。
2.2.2 开放度函数
考虑路段开放的直接效益,即开放后对小区内部交通的促进作用,算式为
(8)
式中:C为小区开放度;Nin与Nout分别为开放小区道路的入口及出口连接的道路数,个;η为惩罚因子,根据预实验将惩罚因子设置为2。
当小区开放道路,入口车道大于出口车道时,导致车辆不能及时离开小区,造成交通堵塞,影响小区内居民,因此应惩罚此种现象;反之则应该鼓励。当某个小区的内部道路C≤2时,此路段不予开放。
2.2.3 约束条件
模型约束条件为
δ∈{0,1}
(9)
式中:δ为封闭小区是否开放。
3 模型求解算法设计
如前所述,由于求解的问题是一个典型的NP-hard问题,因此,文中设计了一种增强的北方苍鹰优化算法作为求解手段,Dehghani等[27]于2021年提出北方苍鹰优化算法,该算法模拟北方苍鹰猎捕猎物时的行为。
3.1 改进的北方苍鹰优化算法内容
北方苍鹰优化算法已被证明在处理不同的优化问题方面具有优势,但无法完全适用文中所建立的模型,文中对北方苍鹰优化算法进行两点改进。第一,由于北方苍鹰优化算法只适用于单目标优化问题,文中是多目标优化问题,所以需要对北方苍鹰优化算法进行改进,使其能解决多目标优化问题。第二,北方苍鹰优化算法的搜索空间是连续的,它不能解决整数优化问题,而文中所要解决的问题可行空间符合约束的0~1序列,因此,需要一个离散的搜索空间和优化规则来改进北方苍鹰优化算法。结合传统北方苍鹰优化算法和0~1编码的特点,对北方苍鹰优化算法进行改进,使其能够解决离散问题。改进后的北方苍鹰优化算法主要思想包含以下三点:
1)基于传统北方苍鹰优化算法的全局搜索和局部搜索的双重搜索;
2)基于0~1编码的解决方案更新方法;
3)多目标问题的Pareto优势思想及拥挤距离机制。
3.2 算法求解步骤
步骤1:初始化种群。根据北方苍鹰优化算法形成满足封闭小区开放的初始化数据,便于后续的迭代优化。
步骤2:初始个体离散重组。为提高初始个体质量,文中引入两类离散重组算子,随机选取一类算子,在初始个体形成后对其进行优化,然后对优化后的初始个体进行帕累托支配和拥挤距离计算,更新初始个体,选择最优个体。重组方法有2种:
1)在初始个体中随机选择两点,将两点交叉,如图1所示;
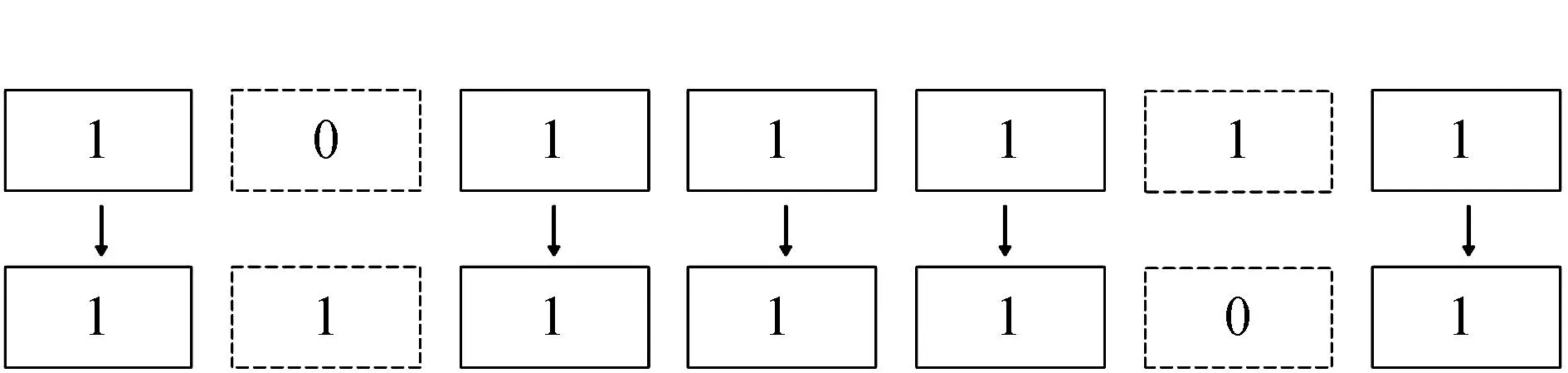
图1 第一种重组方法
2)在初始个体中随机选择两个点,将其放置在初始个体的最后两个点位置上,如图2所示。

图2 第二种重组方法
步骤3:识别猎物及攻击猎物(全局搜索)。在这一阶段,文中还提出了两种类型的个体优化策略,将待优化的个体与步骤2中的最优个体融合,有效提高了个体的多样性。
1)在待优化的个体中随机选择一个分段,在步骤2中选择的最优个体中找到一个分段,将待优化个体的部分按照最优个体进行替换,按照图3顺序更新。
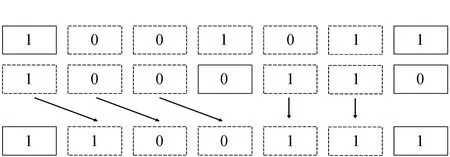
图3 第一种全局搜索策略
2)在步骤2选择的最优个体中随机选择一段,在需要优化替换的个体中找到该段的相同位置进行替换,如图4所示。

图4 第二种全局搜索策略
根据自适应概率R选择两种全局搜索策略,R的算式如式(10)所示。
(10)
式中:M为当前迭代次数;Maxit为最大迭代次数。
当|R|≥0.01时,选择第一个全局搜索策略更新个体;当|R|<0.01时,选择第二种全局搜索策略更新个体。如果优化后的个体适合度高于原个体,则替换优化后的个体。
步骤4:追逐及逃生(局部搜索)。ENGO中采取产生随机数和0~1互换的方式进行局部搜索,分为以下两步:
1)产生随机数,这一步决定了对几个个体执行搜索过程,若随机数为6,则随机选择6个个体;
CMDS软件初筛结合人工审核模式在我院中成药处方点评中的应用实践 ………………………………… 沈剑文等(16):2278
2)将选择个体中的0~1进行互换。如图5所示。
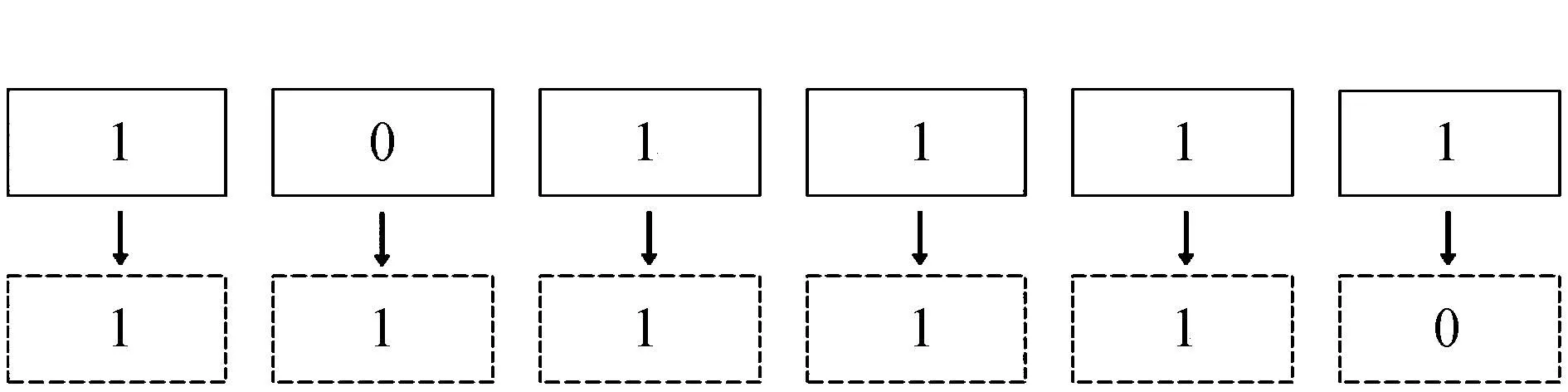
图5 局部搜索策略
步骤5:帕累托优势和拥挤度距离计算。优化完成后,计算个体的帕累托支配和拥挤距离,将非支配解保存到外部存档中,并根据拥挤距离更新最优个体。外部在每次迭代后更新以进行优化,直到达到最大迭代次数。
4 算例分析
4.1 网络设计
虚拟道路网络共有22个交叉口、70条路段,此路网中共有5个封闭小区A、B、C、D、E,每个封闭小区内部均两条路段,共有10条封闭小区内部道路需要决策。虚拟道路网络如图6所示。
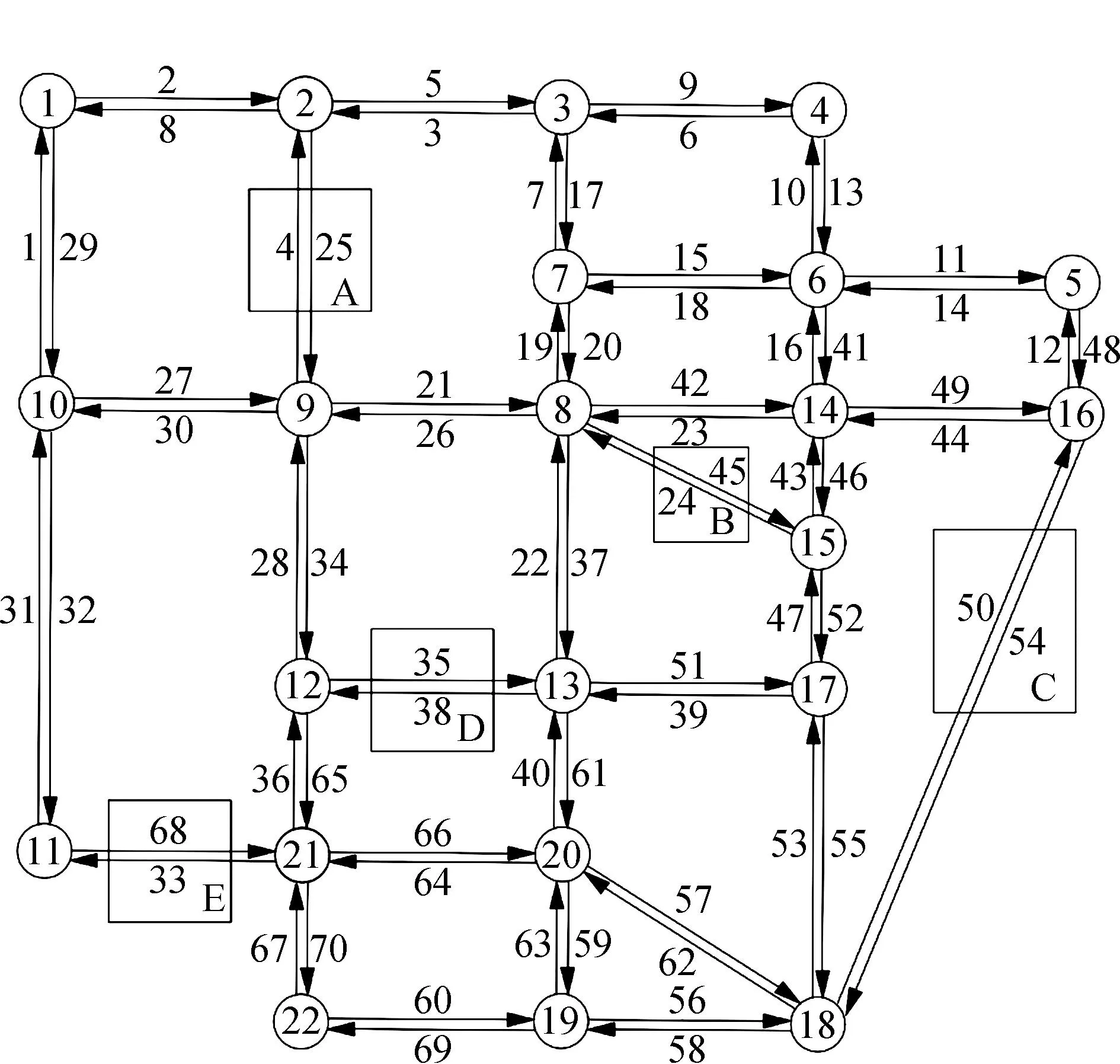
图6 虚拟路网
4.2 ENGO参数校准
首先对ENGO参数进行校准,考虑到给决策者更多的决策空间,外部档案数量被设置为10,对于初始种群数量(Npop)和最大迭代次数(Maxit),根据文献分析和预实验[28-29],给定这两个参数各3个参考值,并进行组合实验以分析其对算法性能的影响,以各参数组合下算法优化问题的比例(IF)和程序运行时间(CPU)作为算法性能的评价标准,IF越大,证明算法性能越好,CPU则相反。由于智能算法具有随机性,为公平,每个参数的实验进行15次并取其平均值。
IF算式如式(11)所示。
(11)
式中:PEinitial为所有初始解目标函数值和的平均值,PEuptade为程序结束后优化得到的帕累托非支配解集的目标函数值和的平均值。
参数的参考值设置和最终结果如表2所示。
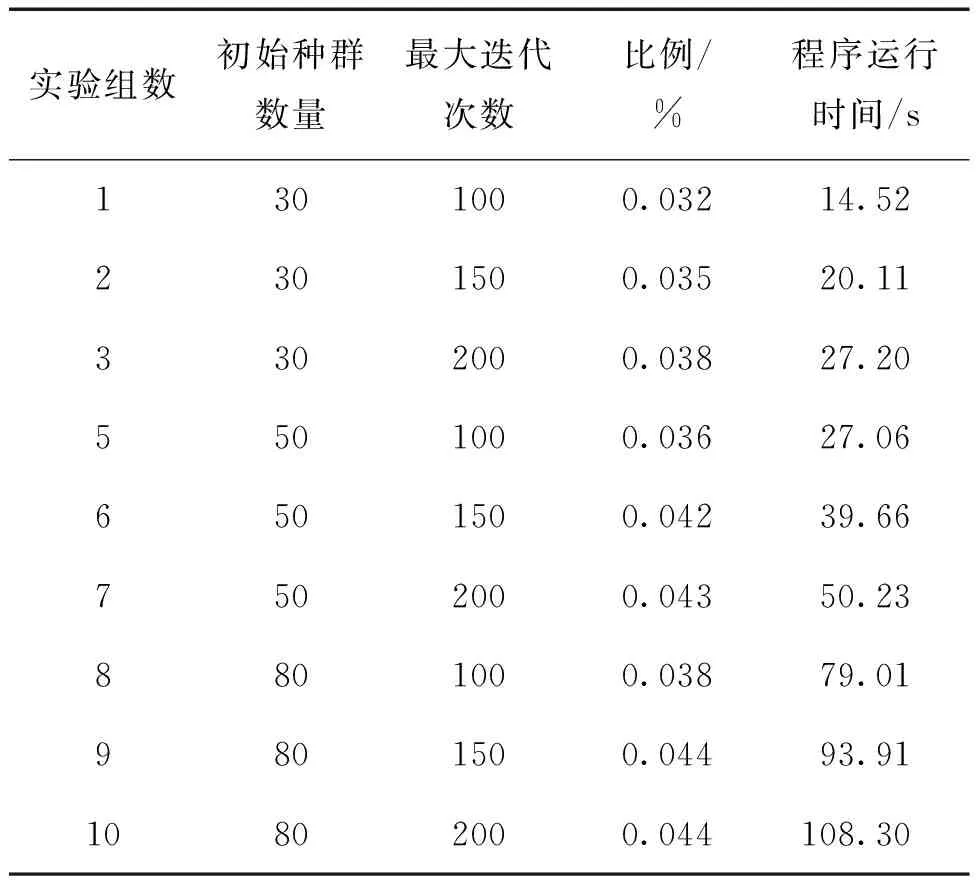
表2 参数校准结果
根据表2中的结果,尽管所有实验次数的最优值为0.044(如第9组),但是其程序运行时间与第7组实验时却多了46.5%,因此,为最大化求解质量和效率的平衡,选择第7组参数组合,设置Npop为50,Maxit为200。对于其它参数,车辆出行产生的费用只考虑能源消耗,按照1.6 L燃油车计算,燃油费为9元·h-1。出行者时间价值取9元·h-1[30]。NOX、HC、CO相对应的治理费用分别为8.36元·kg-1、3.34元·kg-1、1.05元·kg-1。噪声处理费用根据平均费用法进行计算[31],根据预实验,小区开放后通过小区内部道路的速度V被设置为40 km·h-1。
4.3 仿真结果
结合上一节校准后的参数,程序运行一次后得到的帕累托解如表3所示。根据表3中的结果,若决策者需要系统费用值最小,应选择方案5,即开放E小区的路段33。若决策者需要开放度最大,应选择方案4,即开放路段编号为4、24、25、35、38、45、50、54、68。经过排序,综合考虑系统费用值和开放度,应选择方案7,其系统费用值和开放度均处于中等水平,达到了两个目标之间的均衡,即开放路段编号为4、24、25、35、38、68。
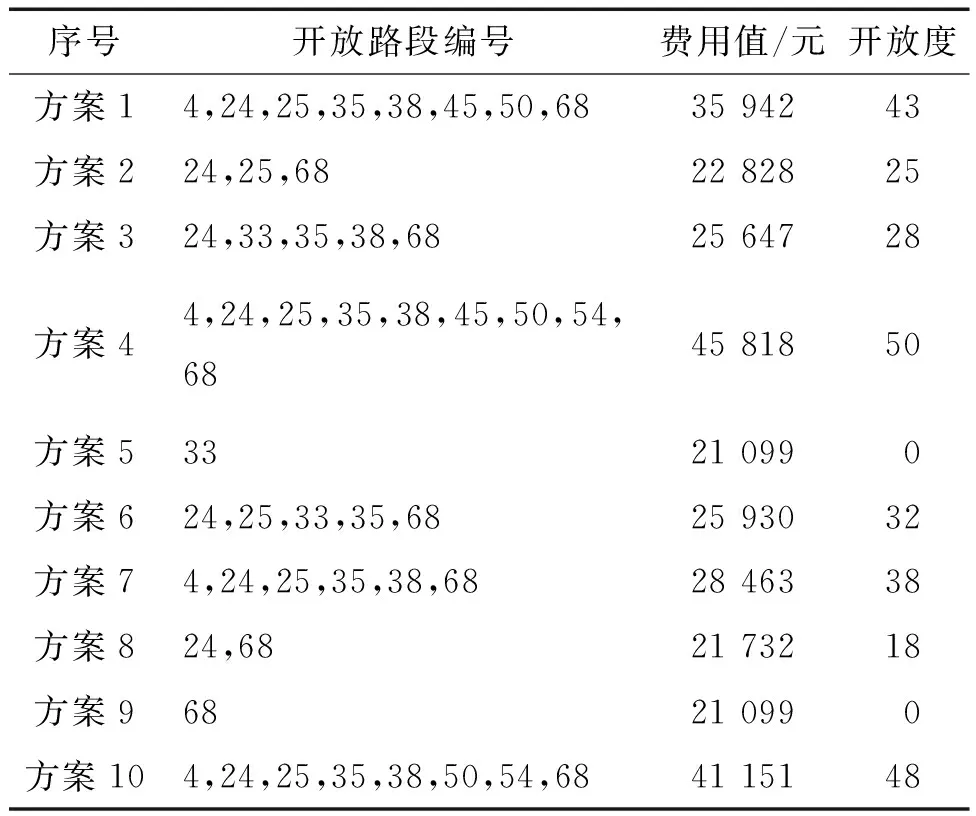
表3 帕累托解
4.3.2 灵敏度分析
研究选取对模型影响最大的变量V进行灵敏度分析,此时速度修正因子不发生变化。每个速度都会产生10个帕累托解,将每个速度下的费用值和开放度的平均值进行比较,计算后得到的费用值及开放度如表4所示。

表4 不同速度对应的封闭小区开放费用值及开放度
根据表4数据可知,不同速度对费用值和开放度有较大影响。速度取15 km·h-1时开放度最大,速度取60 km·h-1时费用值最低。尽管速度为55 km·h-1和60 km·h-1时开放小区产生的费用值较小,但这与实际城市通行速度不符,此时费用值较小的原因是由于速度过高导致多个小区的路段不适宜开放,所以此时的开放度较低。根据不同速度下费用值和开放度对比,可得速度应设置在40 km·h-1以内最为合理。当速度为40 km·h-1以内时,速度取15 km·h-1时开放度最大,速度取40 km·h-1时费用值最小。ENGO为改进的北方苍鹰优化算法,NSGA-Ⅱ为非支配排序遗传算法,SEO为多目标社会工程优化器算法。
4.4 算法性能分析
为进一步验证ENGO的有效性,将ENGO的求解结果与非支配排序遗传算法[32](NSGA-Ⅱ)和社会工程优化器[33](SEO)进行比较,由于这两种算法的传统版本同样是解决连续优化问题,所以选择文献中开发的这两种算法的离散版本,并采用与ENGO相同的编码方法。
选择增强的反世代距离(IGD)、超体积(HV)和CPU 3个重要指标来评价算法性能,IGD值越小,表明解集的收敛性和多样性更好,HV指标数值越大表示算法的综合性能越好。此外,为了从多角度进行算法性能衡量,本节将初始种群设置为50、80,迭代次数设置为200、500,其它参数设置与上述相同,HV参考点被设置为(1,1,1),IGD-NS需要的真实帕累托前沿由几种算法合并获得,最终结果如表5所示。表5中Npop代表初始种群数量,Maxit代表最大迭代次数。
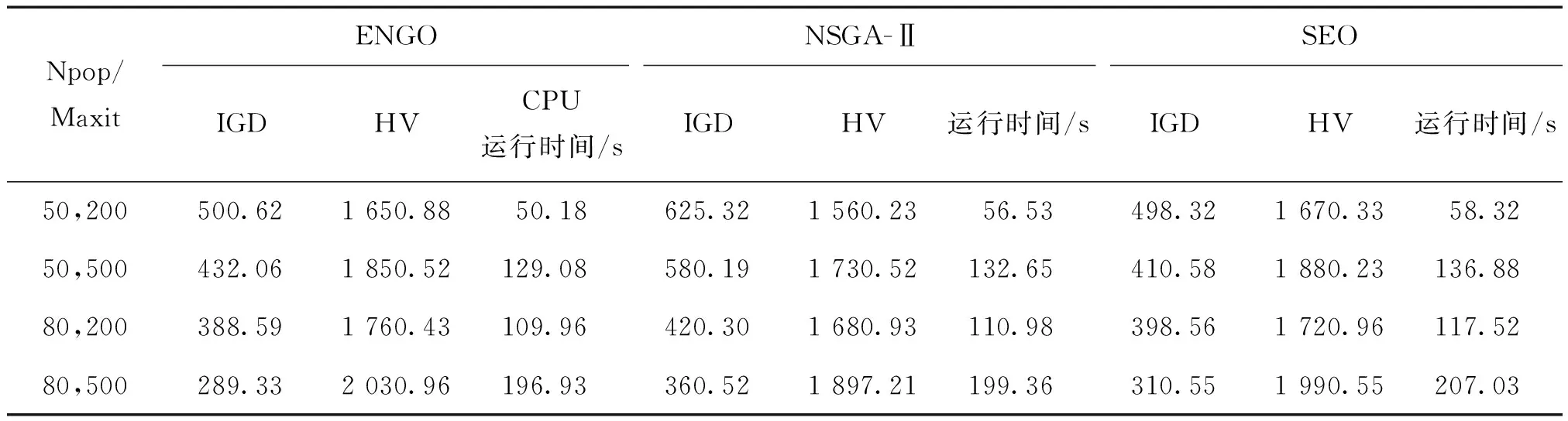
表5 算法性能比较
由表6可得,在种群规模较小时,社会工程优化器算法取得了超体积的最优值,改进北方苍鹰算法取得了运行时间的最优值,此外,其超体积数值与社会工程算法相差无几。随着种群规模的增加,改进的北方苍鹰优化算法的优势凸显扩大,取得了超体积、运行时间、反世代距离的最优值,证明改进的北方苍鹰优化算法的有效性,以及求解时间和求解效率上的高度平衡性。研究结果表明,ENGO的反世代距离平均值相比NSGA-Ⅱ提升了18.19%,相比SEO提升了0.98%。ENGO的超体积平均值相比NSGA-Ⅱ提升了6.05%,相比SEO提升了0.37%。ENGO的运行时间平均值相比NSGA-Ⅱ减少了4.01%,相比SEO减少了7.74%,ENGO相比其他两种算法在性能上有了显著提升,运算速度更快。

表6 算法性能百分比差距比较 %
5 结 论
1)基于封闭小区开放后对车辆出行时间以及小区内部安全问题、汽车尾气排放污染和交通噪声污染等方面产生的影响,构建费用值最小和开放度最大的多目标优化模型,优化封闭小区的开放策略。将封闭小区开放后的安全隐患、交通污染、交通噪声转换为费用值,考虑出口和入口的数量关系,用费用值和开放度衡量小区开放后的效果。对广义费用值函数中的速度参数进行灵敏度分析,得到速度对封闭小区开放决策有显著影响、较高的限速值会带来最优开放方案的结果。细化封闭小区开放决策方式,加入封闭小区是否开放和单双行的决策方式,使得封闭小区开放策略更为合理。当封闭小区开放后,不同区域、位置的封闭小区应选择不同的开放方案。
2)考虑到北方苍鹰算法在求解NP-Hard问题方面的优势,重新设计了算法的编码和优化规则,引入离散算子和局部搜索算子,以提高算法的搜索性能。使用增强的北方苍鹰算法对模型进行求解,求得的开放政策最优,且模型运行稳定。提出的算法能实现模型的稳定运行,将改进的北苍鹰算法与多目标社会工程优化器算法和非支配排序遗传算法在性能上进行比较,ENGO的反世代距离相和超体积性能相比于其它两种算法均有显著提高,运算时间减少、运算速度加快,证明改进的北方苍鹰算法的有效性。
3)构建的封闭小区多目标开放策略模型对制定封闭小区的开放策略有一定借鉴意义,但在研究中着重考虑了费用与开放程度,后续研究还需要进一步考虑其它因素,如人的主观因素、小区规模等对小区开放决策的影响。
