考虑碳排放控制的建筑废弃物运输系统优化

2024-01-20赵佳虹叶子欣刘思雨

交通科技与经济 2024年1期

乌婕,赵佳虹,叶子欣,刘思雨

(广东工业大学土木与交通工程学院, 广州 510006)

随着城市现代化建设的不断推进,建筑废弃物的产量逐年递增,给城市废弃物运输系统的节能减排和生态环境造成了巨大威胁。通常的建筑废弃物运输系统包含运输、分类、回收、处置等多个环节,合理评估运输全过程的碳排放量和环境影响,优化设施选址、运输路径设计和运量分配决策,是实现城市交通运输系统可持续发展的关键问题。

近年来,国内外学者对废弃物回收管理领域的碳排放计算、系统优化建模和求解方法设计等内容进行了大量研究。Shi等[1]将二氧化碳排放系数引入到废弃物的环境风险度量模型中;Rahimi等[2]以碳排放作为环境影响评估标准,并构建度量模型;吴昆仑等[3]以二氧化碳排放成本衡量环境负影响;胡鸣明等[4]以运输成本最小化为目标,构建建筑废弃物处理厂选址模型; Xu等[5]针对建筑废弃物多周期性,建立逆向物流模型;Liu等[6]引入环境负效应目标,建立废弃物回收厂选址模型;Hu等[7]建立不确定条件下的两阶段选址模型;赵佳虹等[8]构建废物运输的选址-路径模型;陈彦等[9]以车辆行走距离最小为目标,优化垃圾回收路线;Fu等[10]提出了一种基于成本与回收率权衡的政府补贴建筑垃圾回收逆向物流网络模型,并采用改进粒子群算法,求解双目标问题;Prasit等[11]采用加权切比雪夫方法,求解感染性废物的处置优化问题;Rabnawaz等[12]使用混合整数线性规划技术,求解多阶段建筑废弃物逆向物流模型;Diba等[13]引入元启发式算法,设计危险废物多目标选址-路径鲁棒优化问题的求解步骤;古红霞等[14]以成本与满意度为目标,构建多目标选址-路径模型,设计带精英策略的快速非支配排序遗传算法对多目标进行求解;Ebadi等[15]考虑成本、运输中的环境风险和排放及就业机会,构建多目标模型,并提出一种改进的多选择目标编程(IMCGP)方法来求解多目标优化模型。

综上所述,已有研究成果主要在碳排放度量、风险度量以及研究决策方面存在欠缺。鉴于此,文中考虑碳排放和环境风险的复合影响,协同优化设施选址、运输路径选择和运量分配决策,并基于“TOPSIS-遗传算法”设计两阶段求解步骤,以实例和测试算例来验证模型和求解方法的有效性、稳定性和参数敏感性。

1 碳排放和环境风险度量

在建筑废弃物的运输过程中,会排放大量的二氧化碳。由于废弃物含有大量的粉尘等颗粒物,若运输过程中突发事故,也会造成环境影响。文中将建筑废弃物运输系统的关键设施和运输路段作为潜在排放源和风险源,分别设计碳排放和环境风险度量模型。

1.1 碳排放度量

加工中心和填埋场的碳排放度量:设定u和θ分别为加工中心和填埋场处理建筑废弃物的释放二氧化碳系数,kg·t-1;m和h分别为加工中心和填埋场的建筑废弃物数量,t;C为二氧化碳。则加工中心和填埋场的碳排放量Rc1和Rc2分别为

运输路段的碳排放度量:设xi,j为运输路段(i,j)的建筑废弃物运输量,t;CR为滚动阻力系数,常取0.01;g为重力加速度,m·s-2;Vi,j为车辆在路段(i,j)上的平均行驶速度,km·h-1;CD为空气阻力系数,常取0.70;A为车前端表面积,m2;ρ为空气密度,kg·m-3;η为汽车转动功率,常取0.40。则发动机输出功率P为

(3)

设τ为车辆燃料的二氧化碳转化系数,kg·L-1;ε为燃料空气质量比,常取1.00;σ为发动机摩擦系数,kJ·RL-1;N为发动机转速,r·s-1;M为发动机排量,L;δ为发动机效率系数,常取0.90;Di,j为运输路段(i,j)长度,km;μ为燃料热值,kJ·g-1;φ为转换因子,常取840。整合式(1),推导出运输过程中的碳排放量RC3为

(4)

整合式(1)～(4),建筑废弃物运输系统的碳排放量RC可计为

(5)

1.2 环境风险度量

建筑废弃物在运输过程中会释放大量颗粒物,运输路段周边居民吸入的颗粒物数量反映了运输建筑废弃物的环境风险。根据颗粒物的环境传播特性,将建筑废弃物的环境风险定义为:在运输路段的一定区域范围内,建筑废弃物释放的颗粒物浓度与周边常住人口数量的乘积。设定F为单位时间内每吨建筑废弃物释放的颗粒物浓度,kg·t-1h-1;POPi,j为路段(i,j)附近的人口数量,人;e代表环境,则建筑废弃物的环境风险Re表示为

(6)

2 数学模型

2.1 问题描述

根据回收利用程度,可将建筑废弃物分为可分类、可加工、可回收和可填埋4个种类。如图1所示,建筑废弃物运输系统包含了建筑废弃物的产生点、分类中心、加工中心、填埋场和建材供应商。可分类的建筑废弃物从产生点运输至分类中心,形成可加工的建筑废弃物;可加工的建筑废弃物由加工中心进行技术处理,生成可回收的建筑废弃物,并运往建材供应商进行回收再利用;在分类和加工中心生成的可填埋建筑废弃物,将运往填埋场进行集中处置。基于此,文中研究的建筑废弃物运输系统优化问题,是在运输网络中,协同优化多个分类中心和加工中心的建设位置、运输路线设计和运输量分配决策。

图1 建筑废弃物运输系统

2.2 构建模型

2.2.1 基本假设

1)运输网络的交通环境相对稳定,各运输路段无容量限制;

2)各类设施和运输车辆都满足处理和运输建筑废弃物的安全要求;

3)各类建筑废弃物满足处理相容性条件,可同时在同一设施中混合处理。

2.2.2 符号说明

符号说明如表1所示。

2.2.3 多目标选址-选线模型

minf1=RC

(7)

minf2=Re

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

ri≤JCipi, ∀i∈J

(16)

mi≤BCioi, ∀i∈B

(17)

hi≤DCi, ∀i∈D

(18)

xi,j≥0, ∀i∈I, ∀j∈J

(19)

yi,j≥0, ∀i∈J, ∀j∈B

(20)

zi,j≥0, ∀i∈J, ∀j∈D

(21)

ui,j≥0, ∀i∈B, ∀j∈D

(22)

ni,j≥0, ∀i∈B, ∀j∈L

(23)

ri≥0, ∀i∈J

(24)

mi≥0, ∀i∈B

(25)

hi≥0, ∀i∈D

(26)

式(7)～(9)为目标函数,其中式(7)为最小化总碳排放量,主要包括加工中心、填埋场和运输路段的碳排放量;式(8)为最小化总环境风险,主要包括各运输路段的环境风险;式(9)为最小化总成本,主要包括分类中心和加工中心建设成本、运营成本、运输成本。式(10)～(15)为流量平衡约束,其中:式(10)～(11)表示产生点与分类中心之间的流量守恒;式(12)～(13)表示分类中心与加工中心、填埋场之间的流量守恒;式(14)～(15)表示加工中心与建材供应商、填埋场之间的流量守恒。式(16)～(18)表示分类中心、加工中心和填埋场的最大能力约束;式(19)～(26)表示连续决策变量定义域。

3 求解方法

文中建立的是一个多目标0～1混合整数线性规划模型,模型为含有3个不同量纲的目标函数,采用分阶段求解思路,将选址-选线的组合优化问题分解为设施选址和选线-运量分配两个子问题,分别基于TOPSIS方法[16-18]和遗传算法[19-21]设计求解步骤,具体流程如图2所示。

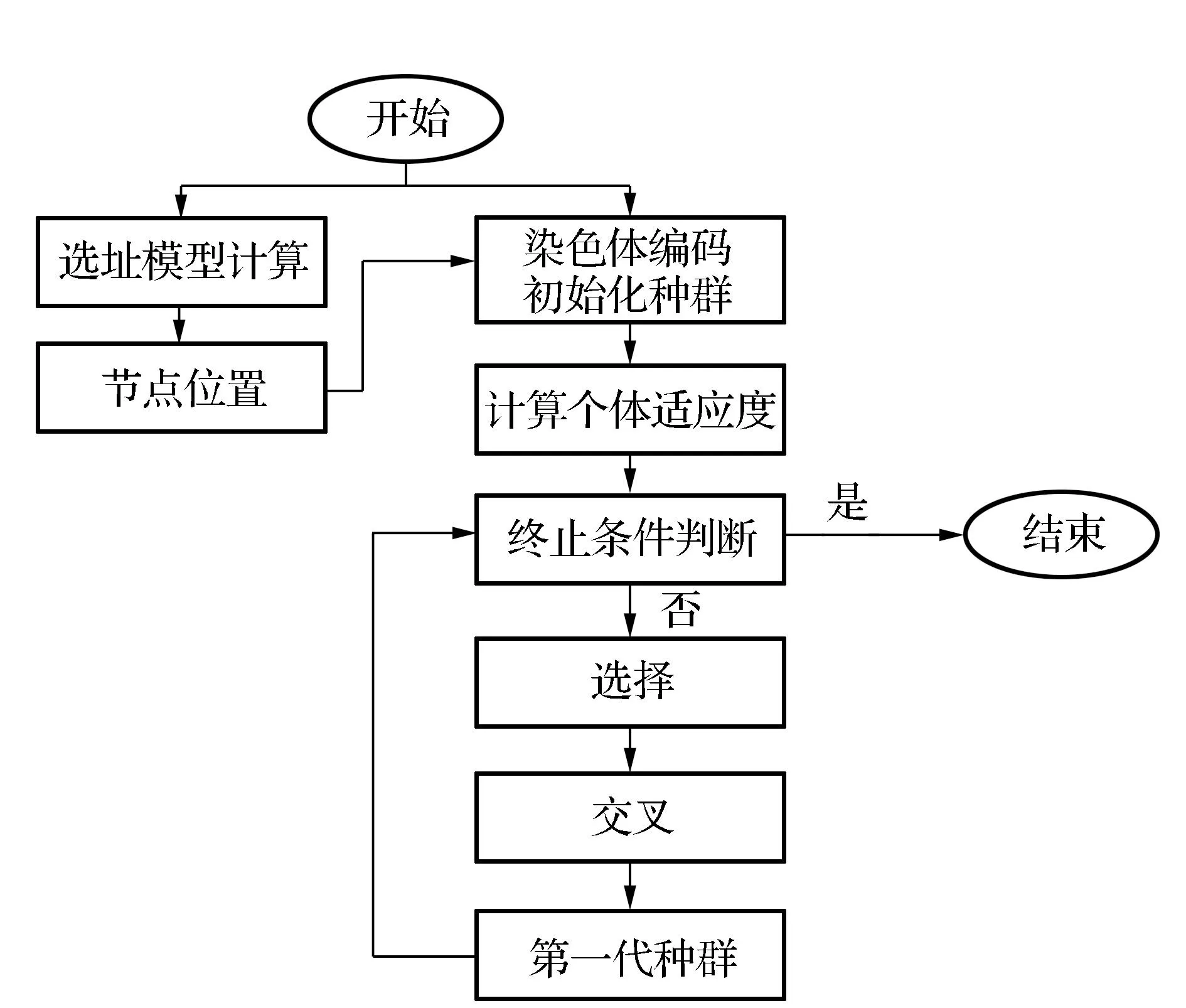
图2 分阶段求解流程

3.1 基于TOPSIS方法的选址子问题算法设计

步骤1:选址子问题模型构建。由于文中的总成本和碳排放目标函数与选址决策相关,因此选取原多目标模型中的选址决策变量及其关联的约束条件,并分别构造总成本和碳排放量的目标函数。

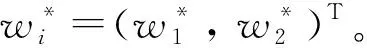
步骤3:引入转换系数gi,i=1,2,采用极值法[22]对各单目标进行无量纲化处理。

(27)

步骤4:设定各子目标的权重系数λi,i=1,2。

步骤5:运用TOPSIS方法,将多目标优化模型转化为如下单目标优化模型

(28)

3.2 基于遗传算法的运输路线选择和运量分配子问题算法设计

步骤1:编码。用一个矩阵Ai,j表示一个染色体,即一个可行解(i,j)=(x1,1,x1,2, …,x3m,4n),其中,元素xi,j表示从i点到j点的建筑废弃物运输量,1≤i≤3m, 1≤j≤4n。矩阵每一行i(1,2, …,3m) 由生产点 (1～m)、分类中心(m+1～2m)和加工中心(2m+1～3m)组成,每一列由j分类中心(1～n)、加工中心(n+1～2n)、填埋场(2n+1～3n)和建材供应商(n+1～4n)组成。染色体Ai,j满足模型设定的流量守恒和设施能力约束[23]。

步骤2:随机生成初始种群。设定初始种群规模NS,生成初始种群集合NP,最大迭代次数设定为NG。初始种群记为P(0),则第t代种群记为P(t)。

(29)

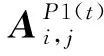
步骤6:终止。当t+1=NG时,即种群代数等于最大迭代次数时,则终止;否则,转至步骤3。

4 算例分析

文中采用1个实例和10个测试算例来验证模型和算法的有效性、参数敏感性和稳定性。其中,基础算例以深圳市的建筑废弃物运输管理为背景,测试算例为基础算例的数据规模拓展。所有算例都在CPU为Intel(R) Pentium(R) G4560 1.70 GHz、RAM 16.00 GB环境下,利用python编程,调用Gurobi 9.5.2进行求解。

深圳市建筑废弃物运输系统共含有19个产生点(节点1～19),11个分类中心建设候选点(节点20～30),12个加工中心建设候选点(节点31～42),6个填埋场(节点43～48)和10个建材供应商节点(节点49～58)。根据文献[11-12]的参数设置方法,设定各产生点的建筑废弃物产量如表2所示。分类中心建设候选点的固定建设成本为1万元·个-1,单位变动成本和最大处理能力如表3所示。加工中心建设候选点的固定建设成本为50万元·个-1,单位运营成本45元·t-1,最大处理能力为7万t·a-1;填埋场的单位运营成本为35元·t-1;建筑废弃物的单位运输成本为2元·km-1;运输车辆的平均行驶速度为40 km·h-1。

表2 建筑废弃物产生点信息

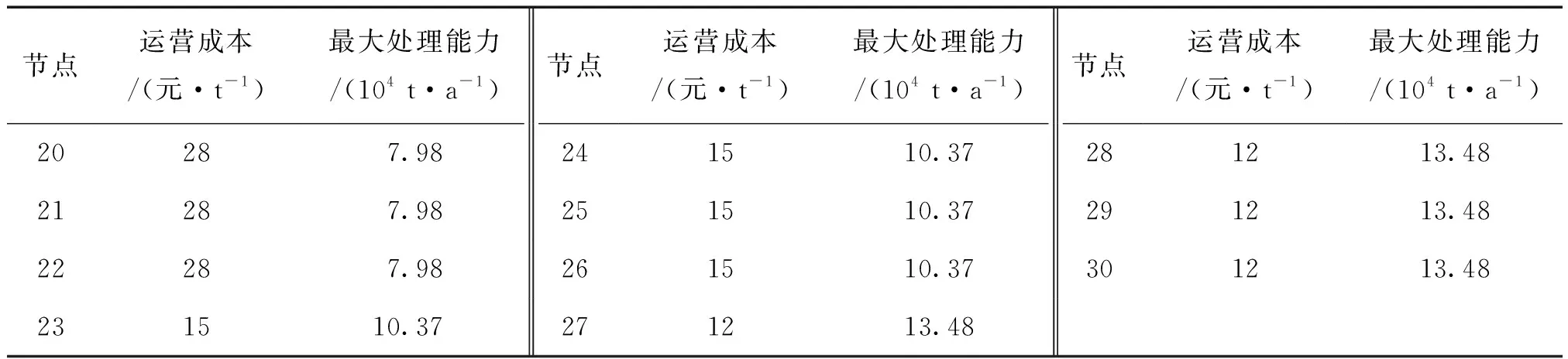
表3 分类中心候选点

4.1 计算结果

设定初始种群数为100,交叉概率为0.8,最大迭代数100,新建的模型和求解方法能够在310 s以内,为含有47 830 66个约束条件和747 660个决策变量的优化问题,求得总成本为1.06×108元、碳排放量为2.96×107kg和总环境风险为1.77×107kg 的优化方案,方案具体信息如表4所示,算法收敛曲线如图3所示。

表4 最优方案

图3 求解收敛曲线

4.2 结果分析

如表5所示,将求得的优化方案与基础算例的现有方案进行对比可知:相较于现有方案,新方案能够在分别降低52.72%的总碳排放量和12.32%的总环境风险的同时,只增加58.21%的总成本。

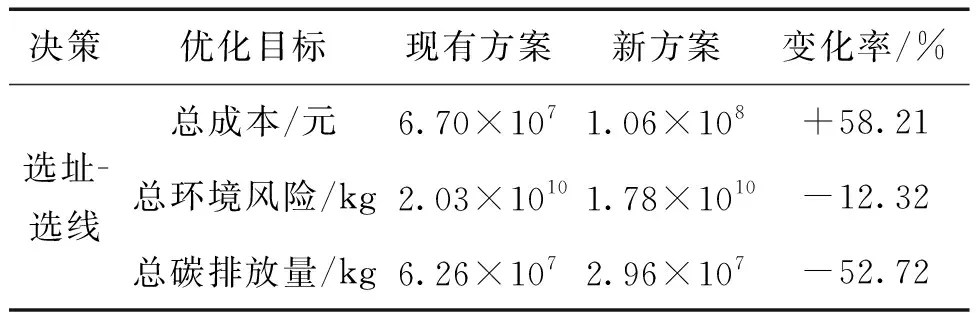
表5 优化方案对比结果

4.3 测试分析

基于深圳市实例,设定测试条件,生成多个测试算例,验证新模型和算法在碳排放度量、风险度量、求解方法设计、参数敏感性和计算稳定性方面的有效性。

碳排放度量模型对比:构造只含有总成本最小和总环境风险最小的建筑废弃物运输系统优化模型,将其求得的优化方案与深圳实例的优化方案进行对比分析。如表6所示,引入碳排放量度量模型,能够降低52.72%的碳排放总量。

表6 碳排放度量模型对比结果

风险度量模型对比:根据设计的求解方法,对比分析传统风险和新建风险度量模型的优化结果。如表7所示,相较于传统的风险度量方法,新建的环境风险度量模型能够分别降低11.76%的成本和0.65%的碳排放量。

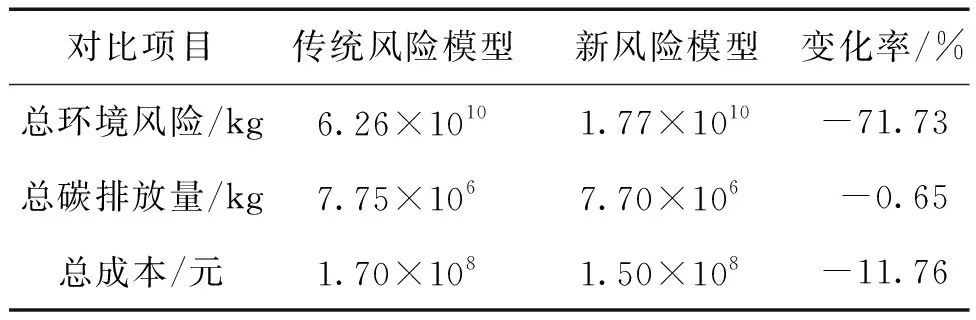
表7 风险度量模型对比结果

求解方法对比:在同样的计算环境下,分别采用常规的多目标优化方法和新算法来求解实际算例,其中,常规多目标优化方法采用权重目标规划方法,设定3个子目标的权重系数分别为0.2、0.6和0.2。计算结果对比如表8所示:新算法能够求得总成本和总环境风险值更小的解,其解的平均优化程度改进了14.29%。

表8 求解方法对比结果

参数敏感性分析:以深圳市实例为基础算例,设定不同情景进行参数敏感性分析。情景1:加工中心的最大处理能力降低50%;情景2:人口密度降低50%;情景3:车辆行驶速度增为80 km·h-1;情景4:建筑废弃物的颗粒物释放系数降低20%;情景5:填埋场的二氧化碳系数降低50%。结果如图4所示:降低加工中心的最大处理能力,总成本和总风险将分别增加1.35%和44.66%;降低人口密度,总风险降低49.6%;增加车辆行驶速度,总风险降低39.8%;降低颗粒物释放系数,可降低20%的总风险;降低填埋场的二氧化碳系数,总成本、总碳排放量和总环境风险分别降低14.23%、21.11%和99.38%。