基于阻塞流的配电网安全边界快速算法

2024-01-20屈玉清

天津大学学报(自然科学与工程技术版) 2024年3期

屈玉清，肖峻，焦衡，孙纲

(1.智能电网教育部重点实验室(天津大学)，天津 300072；2.山东理工大学电气与电子工程学院，淄博 255000)

相较输电网，配电网一般不需考虑稳定问题，其稳态问题与网络流问题更接近，因此网络流理论可应用于配电网[1-5].文献[1]提出了基于动态网络流模型的配电网和地铁网的弹性评估方法，将问题简化为线性规划问题，降低了计算复杂度.文献[2]提出了基于网络流转移分布因子的主动配电网风险评估与预警方法，大幅减小了计算时间.文献[3]提出了基于最小费用最大流模型的配电网经济优化有功调度计算方法，将问题简化为线性规划问题，减少了计算时间.文献[4]提出了基于网络流的配电网规划优化算法，简化了计算.文献[5]提出了基于最大流的配电网线损计算方法，简化了节点编号及原始数据准备.可见，将网络流理论应用于配电网，能简化问题，提高计算效率.

在智能电网背景下[6]，2012 年，文献[7]提出了配电网安全域(distribution system security region，DSSR)的概念.DSSR 定义为配电网满足给定安全约束的工作点集合[7-8]，描述了配电网的最大允许运行范围，是研究配电网的一个基本问题，在配电网规划和运行中具有重要价值.现有研究已建立起DSSR 理论体系，研究涉及DSSR 的模型[9-10]、求解算法[8,11-12]及应用[13-15]，并推广到综合能源系统[16-17]、舰船电力系统[18]及能源互联网[19]等领域.安全边界是DSSR边界的最重要组成部分，DSSR 求解的最主要结果就是安全边界[11].安全边界的描述有解析式和边界点两种方式.文献[11]提出了安全边界模型算法，能得到安全边界的解析式.文献[8，12]提出了求解安全边界点的算法.但是求解边界点的现有算法计算效率不高[8,12]，难以适用大规模配电网，本文应用网络流理论解决了这一问题.

文献[20]发现城市配电网与多源多汇网具有对应关系，配电网严格安全边界点的本质就是流量网的阻塞流.受此启发，本文基于阻塞流提出了新的配电网安全边界算法，大幅提高了求解效率.

配电网安全边界由严格边界和非严格边界组成[11].对于严格边界，任何负荷单独增加任意小值都会导致不安全，考虑到严格边界与阻塞流的对应，本文选择严格边界为研究对象.网络流研究一般未考虑元件的N-1 失效，因此本文选择正常运行约束(即N-0 安全)[8]下的安全边界进行研究.还有文献定义了堵塞流[21]及饱和流[22]，其本质上都与阻塞流相同，故本文统一采用阻塞流.

1 定义与模型

1.1 配电网安全边界模型

城市配电网的供电路径较短，电压降及功率损耗较小，容量约束比电压约束更严格，故安全边界模型可采用直流潮流模型[8,11,14].工作点为由馈线或馈线段负荷组成的向量.馈线或馈线段负荷等于所属该馈线或馈线段的节点负荷之和.采用馈线或馈线段负荷作为工作点，相对节点负荷，将大大降低安全域的维度.N-0 安全的严格边界模型为

模型约束条件为

式中：∂Ωst0为N-0 安全的严格边界；W＝(SF,1，…，SF,j，…，SF,n)T为工作点；ST,i为主变Ti的负荷；SF,j为馈线Fj的负荷；Sk为馈线段的负荷；cT,i为主变Ti的容量；cF,j为馈线Fj的容量；K 为安全约束系数矩阵，其元素kij≥0；C 为由主变和馈线的容量构成的常向量.

式(2)为主变-馈线的负荷等式约束，表示主变负荷等于其所带馈线负荷之和.式(3)为馈线-馈线段的负荷等式约束，表示馈线负荷等于其馈线段负荷之和；式(4)和式(5)分别为主变容量约束和馈线容量约束，表示主变负荷或馈线负荷都不超过其容量.式(6)为严格临界性约束，由式(2)～式(5)部分不等式取等所得；为矩阵K 所有列向量先做和再做积后不等于零，以保证等式约束能覆盖所有负荷变量，使得所有负荷变量都受到等式约束，保证满足严格临界性[11].

1.2 流量网阻塞流模型

1.2.1 阻塞流

阻塞流是从源点到汇点的每条路径都包含至少一条饱和边(边流量等于其容量)的可行流[22-23]，记为fB.阻塞流模型为

模型约束条件为

式中：f 为网络流，是边集A 上的实函数f：N×N→R；A＝{a1，…，ak，…，an}为边的集合(边集)，ak为第k条边；N＝{I，S，T}为节点的集合；I＝{i1，…，ij，…，ip}为除S 和T 外的中间节点的集合，ij为第i 个中间节点；S＝{s1，…，sj，…，sk}为源点的集合(源点集)，sj为第j 个源点；T＝{t1，…，tj，…，tm}为汇点的集合(汇点集)，tj为第j 个汇点；val(f)为网络流f 的流量，即流出源点集的流量之和；fk为边ak的流量；非负实数集c＝{c1，…，ck，…，cn}为边的容量集，ck为边ak的容量；P＝{P1，…，Pj，…，Pm}为从源点到汇点的所有路径的集合，Pj为第j 条从源点到汇点的路径.

式(8)～式(10)为平衡约束，其中式(8)表示源点集的净输出量等于网络流的流量，式(9)表示汇点集的净输入量等于网络流的流量，式(10)为流量守恒约束，表示除源点集和汇点集外的中间节点的净输出量为零，即中间节点的流入流量等于其流出流量.式(11)为容量约束，表示任意边的流量都不超过其容量.式(12)为饱和边约束，表示从源点到汇点的每条路径都包含至少一条饱和边，则当任何边增加任意小流量时，一定导致边流量超过其容量(过载).需指出，本文与经典网络流理论一致，即研究阻塞流时不考虑损耗[21-23].

1.2.2 阻塞流集

为与配电网严格边界对比，定义阻塞流集为网络所有阻塞流的集合，记为FB，模型为

1.3 安全边界与阻塞流的对应关系

从定义上看，严格边界点和阻塞流虽有差异，但并不矛盾，恰好体现了因果关系如下.

(1) 阻塞流定义中的每条路径都包含至少1 条饱和边，等价于严格临界性，原因是：当阻塞流fB的任何边增加任意小流量生成新流f′时，由于f′需满足平衡约束和容量约束，而每条路径都包含至少1 条饱和边，这将导致f′至少有1 条边过载，即新流变成了不可行流.不可行流是不满足容量约束的网络流.故阻塞流具有严格临界性.

(2) 两者的严格临界性相对应.原因是：严格边界点的严格临界性是任何负荷单独增加任意小值，导致网络状态从安全状态变为不安全状态；阻塞流的严格临界性是任何边增加任意小流量，导致网络流从可行流变为不可行流.

(3) 从更深角度解读二者定义的差异，阻塞流的路径饱和是从“因”的角度定义；严格边界点的严格临界性是从“果”的角度定义，两者虽不一样但并不矛盾，恰好体现了因果关系.

从模型上看，安全边界与阻塞流有对应关系如下.

(1) 式(2)的所有主变负荷之和，等价于源点集的净输出量式(8)；式(3)的所有馈线段负荷之和，等价于汇点集的净输入量式(9)；在配电网中，除主变和负荷节点外的其他节点负载净输出量为零，即该类节点的流入功率等于其流出功率，体现了基尔霍夫电流定律，等价于流量守恒约束式(10)，即中间节点的流入流量等于其流出流量.因本文严格边界模型采用馈线段负荷表示工作点，所以模型中未直接体现出基尔霍夫电流定律，但配电网始终满足基尔霍夫电流定律，能对应流量守恒约束.

(2) 式(4)和式(5)分别表示主变容量约束和馈线容量约束，等价于容量约束式(11).

(3) 式(6)表示严格临界性约束，等价于饱和边约束式(12)，因为两者都表示严格临界性.

综上所述，从定义和模型角度对比发现严格边界与阻塞流集对应，严格边界点与阻塞流对应.它们定义角度不同，实为因果关系[20].

严格边界点与阻塞流的对应关系对配电网和流量网络具有重要意义，为两个领域的交叉研究奠定了理论基础，提供了解决问题的新途径，有助于推动两个领域的快速发展.例如，流量网络中新颖的安全分析方法和计算方法能激发配电网安全边界理论的研究，将配电网安全边界理论的研究成果推广到网络流领域.

2 基于阻塞流的配电网安全边界算法

由于流量网阻塞流与配电网严格边界点有很好对应关系.因此可利用阻塞流来求解严格边界解析式和严格边界点.

基于阻塞流的配电网安全边界算法包含如下3个步骤.

步骤1将配电网等效为流量网络.在配电网安全性分析中，对负荷供电无需区分来自哪个电源(变电站主变)，故引入虚拟电源化简网络.

步骤2根据阻塞流模型的式(8)～式(10)平衡约束、式(11)容量约束及式(12)饱和边约束，列写流量网络阻塞流解析式，得到对应的配电网严格边界解析式.

步骤3利用降维采样算法求解阻塞流，得到对应的配电网严格边界点.过程如下.

(1) 降维提高算法效率.边个数为采样的变量维数，为提高算法效率，根据平衡约束和饱和边约束减少采样边个数，具体步骤如下：① 选取源点相连边流量为观测变量，记为Θ；② 根据饱和边约束确定饱和边，饱和边的流量等于边的容量(常量)，记为τ；当Θ 中含有饱和边时，其流量归类为Γ；③ 根据平衡约束，利用 Θ 与τ组合表示其余边流量，记为Π.若边流量无法用τ和Θ 组合表示，则将该边流量归为观测变量；④ 降维后的网络流为f＝{Θ，Γ，Π}.

(2) 采样得到可行流.以一定步长σ 对观测变量采样，得到u 个网络流，然后利用平衡约束和容量约束筛选得到q 个可行流ff.

(3) 饱和边约束校验得到阻塞流(严格边界点).对每个可行流 ffi(i＝1，2，…，q)，校验其是否满足饱和边约束，若满足则是一个阻塞流，即求得一个对应的配电网严格边界点.

算法流程如图1 所示.

图1 基于阻塞流的配电网安全边界算法流程Fig.1 Flow chart of blocking flow-based algorithm for distribution network security boundary

相较现有算法[8,12]，本文算法简化了求解严格边界点的计算过程并加快了计算速度.原因是：①本文算法无需计算安全域边界解析式，而现有算法必须计算，对于大规模配电网，计算安全域边界解析式是耗时的；②本文算法根据平衡约束和饱和边约束，通过降维采样算法减少了采样变量数，所减少的采样变量数大于等于中间节点数.

3 算例验证

传统配电网开环运行，潮流计算和安全分析相对简单.采用电力电子软开关(soft open point，SOP)的柔性配电网合环运行[24]，潮流计算和安全分析更复杂，更适合展示，故算例选择柔性配电网.SOP 是安装在配电网中代替常开点的电力电子设备[25]，具有有功潮流控制、无功补偿、电压调节、快速隔离故障和恢复供电等优点[24-25].

3.1 算例概况

扩展的IEEE RBTS BUS4 柔性配电网算例[26]如图2 所示，共3 座35 kV/10 kV 变电站，9 回10 kV 馈线.导线型号为 YJV22-3×240，负荷功率因数为0.90.馈线F2和F3、F5和F6、F7和F8之间通过SOP柔性互联，合环运行.算例参数如表1 所示.

表1 算例数据Tab.1 Parameters of the example

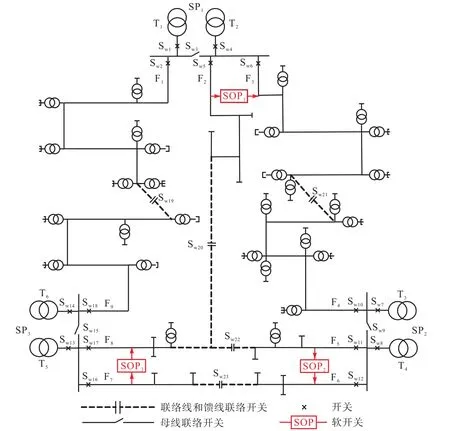
图2 IEEE RBTS BUS4柔性配电网Fig.2 IEEE RBTS BUS4 flexible distribution network

3.2 等效流量网络

将图2 配电网等效为流量网，如图3 所示.

图3 算例的等效流量网Fig.3 Equivalent flow network of the example

从图3 可以看出：加入单一虚拟源节点s，再用足够大容量边将其与已有源节点(变电站10 kV 母线)连接，将多源多汇网络简化为单源多汇网络.这样处理的原因是：在安全性分析中，只需判断负荷是否能供电，而无需区分来自哪个电源.

图2 中SOP 等效为中间节点，考虑了SOP 对潮流的双向调节.以SOP1为例，图2 中SOP1等效为图3 中的中间节点i16；SOP1两端支路等效为边a25和边a26.用正负容量区别双向调节.正向调节时，SOP 两端支路的容量及等效边的容量都取正容量值；反向调节时，都取负容量值.图2 中SOP1为正向调节潮流流向，等效对应图3 中边a25和边a26的流量流向；反向调节时，SOP1两端支路的潮流流向与图2 中相反，等效边的流量流向与图3 中相反.

SOP 除控制有功外，还能向两侧发出或吸收无功来调压，本文研究有功分布，在有功分布合理后可再考虑无功调压[24-25].

网络流理论中，当中间顶点的入度和出度都为1且流入和流出边容量相等时，删除中间顶点及一条边不影响网络等效.将图3 化简后如图4 所示.

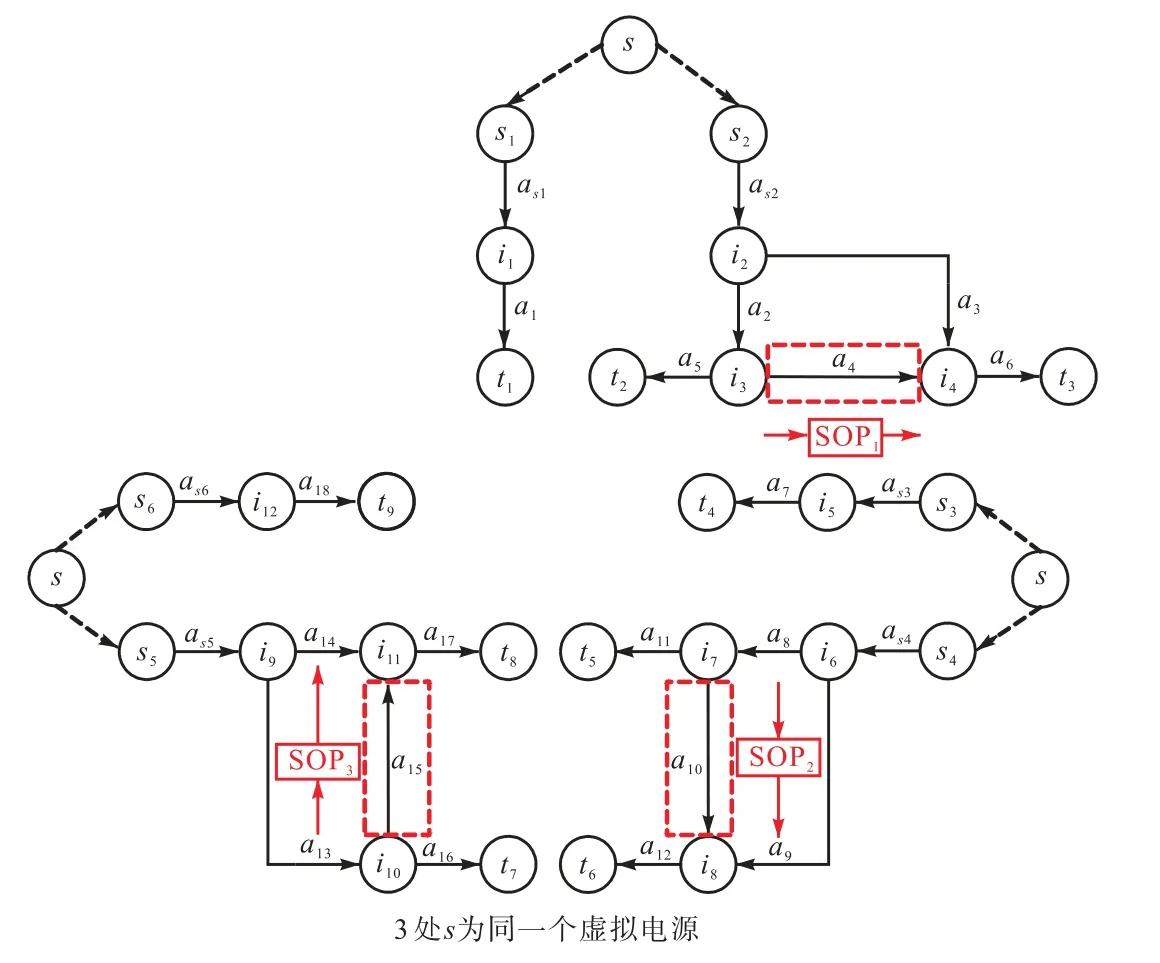
图4 算例的等效化简网Fig.4 Simplified flow network of the example

3.3 阻塞流求解

1) 阻塞流解析式

由第1.2 节阻塞流模型的式(8)～式(10)平衡约束、式(11)容量约束及式(12)饱和边约束，推导图4网络的阻塞流解析式，结果如式(14)～式(21)所示.

(1) f4、f10和f15都为正时有

(2) f4和f10为正、f15为负时有

(3) f4和f15为正、f10为负时有

(4) f4为正、f10和f15为负时有

(5) f4为负、f10和f15为正时有

(6) f4和f15为负、f10为正时有

(7) f4和f10为负、f15为正时有

(8) f4、f10和f15都为负时

式中fk为边ak的流量(k＝1，2，…，18).SOP1正向调节，边a4流量为正，记为f4；反向调节，边a4流量为负，记为.SOP2正向调节，边a10流量为正，记为f10；反向调节，边a10流量为负，记为.SOP3正向调节，边a15流量为正，记为f15；反向调节，边a15流量为负，记为.

由式(14)～式(21)可知，算例等效网络的阻塞流解析式有8 个表达式，这是由于SOP 具有潮流双向调节功能，图2 配电网中的3 台SOP 可以形成8 种潮流的流向状态.这8 种状态可由图4 中边a4、边a10和边a15的流量的正负表征.每一种状态对应一种流量的流通路径，每种流通路径对应一个阻塞流解析式.因此，图4 网络的阻塞流是这8 种状态阻塞流解析式的并集.

2) 阻塞流数据

由第2 节降维采样算法，以2 MV·A 为步长采样共得到125 个阻塞流，结果如表2 所示.经验证，表2 的125 个阻塞流均满足式(14)～式(21)阻塞流解析式，表明采样数据与解析式完全对应.

表2 等效网络阻塞流Tab.2 Blocking flow of the equivalent network MV·A

3.4 安全边界求解

由第1.3 节知，严格边界和阻塞流集对应，严格边界点和阻塞流对应，因此利用阻塞流解析式表示严格边界解析式，阻塞流即为严格边界点数据.

1) 严格边界解析式

根据式(14)～式(21)阻塞流解析式，写出算例的严格边界解析式，结果如式(22)～式(29)所示.

(1) SF2、SF5和SF7都为正时有

(2) SF2和SF5为正、SF7为负时有

(3) SF2和SF7为正、SF5为负时有

(4) SF2为正、SF5和SF7为负时有

(5) SF2为负、SF5和SF7为正时有

(6) SF2和SF7为负、SF5为正时有

(7) SF2和SF5为负、SF7为正时有

(8) SF2、SF5和SF7都为负时有

式中：Li为馈线Fi的等效负荷(i＝1，2，…，9)；SF,i为Fi的出口支路功率(i＝2，3，5，6，7，8)；SOP1正向调节，从F2流入SOP1功率SF2为正；反向调节，SF3为正.SOP2正向调节，从F5流入SOP2功率SF5为正；反向调节，SF6为正.SOP3正向调节，从F7流入SOP3功率SF7为正；反向调节，SF8为正.

2) 严格边界点数据

因阻塞流与严格边界点对应，则算例严格边界点数据同表2 的阻塞流数据相同.所得严格边界点数据还满足电压约束.验证过程如下：对每一个严格边界点，利用OpenDSS 配电网分析软件包进行潮流计算，得到电压偏移，其中最大电压偏移为－2.01%，满足电压偏移国标[－7%，7%].所得严格边界点满足电压约束的原因是：算例属于城市配电网，馈线长度不大，且采用电缆线路，此时电压降不大.研究表明，当馈线长度小于临界长度[27]时，容量约束比电压约束更严格，可采用直流潮流模型进行安全边界计算[27].临界长度主要跟导线型号有关，该算例的临界长度为15.27 km.因此，算例所得严格边界点满足容量约束，故也满足电压约束.

3.5 与现有方法的对比

3.5.1 正确性验证

根据第1.1 节严格边界模型及文献[11]方法求得正常运行约束下的严格边界解析式，与阻塞流算法所得结果(式(22)～式(29))完全相同，故说明正常运行约束下的严格边界与阻塞流在解析式上等价.

利用现有算法[8,12]求解严格边界点，共得到321个边界点，其中125 个与本文结果表2 的125 个阻塞流相同，表明阻塞流算法所得结果是正确的.现有方法多得到了196 个点，它们是额外的，原因是现有算法存在线性规划求解过程和工作点修正过程，该过程产生了额外点.

综上所述，解析式和边界点数据都说明严格边界点与阻塞流有很好的对应关系.

3.5.2 快速性验证

为验证算法快速性，进行仿真实验.仿真环境如下：处理器为 Intel(R)Core(TM)i7-10510U CPU@4.10 GHz，内存为16 GB，操作系统为Microsoft Windows 10，仿真平台为Matlab R2012a.仿真环境的操作系统、CPU 和内存状态会造成运算时间的不同，为减少测量误差，进行20 次实验再平均.

为公平起见，仅比较两种算法所得相同的125 个严格边界点的求解速度.两种算法求解严格边界点的计算性能结果比较如表3 所示.

表3 两种算法的计算性能结果比较Tab.3 Comparison of the computational performance results between the two algorithms

由表3 看出，现有算法用时423.821 s；本文算法用时0.828 s，求解效率提高了511 倍.两种算法在采样步长为2 MV·A 下的总循环求解次数都是91 124次，但本文算法大幅缩短了单次循环求解时间：现有算法单次循环求解时间为4.651 ms，本文算法单次循环求解时间为0.009 ms.本文算法高效的原因是根据网络流理论求解阻塞流，避免了现有算法中耗时的线性规划，分析如下.

(1) 现有算法得到91 124 个方向向量后，需计算每个方向上的严格边界点[8,12].具体方法如下.

步骤1先在TSC 线性规划模型中增加方向向量约束Wy＝kx[8,12]，得到式(30)和式(31).

约束条件为

式中：Wy(y＝1，2，…，91 124)为向量x 的最优解，即向量x 对应的边界点；x 为方向向量，即负荷分布；k 为系数( k∈ R)；Val(x)为所有馈线负荷之和.

然后，利用线性规划软件Lingo 求解式(30)和式(31)，得到向量x 的最优解Wy.

步骤2对每一个最优解Wy，利用严格临界性求解对应的严格边界点[8,12].

步骤1 中的线性规划求解过程耗时占计算时间的80%.

(2) 本文算法得到91 124 个网络流后，先利用式(8)～式(10)平衡约束和式(11)容量约束判断可行流，得到6 860 个可行流，显著缩小了计算范围；再用式(12)饱和边约束判断可行流是否为阻塞流，这一过程没有线性规划求解，速度大幅提高.