带冲突图的着色旅行商问题模型与算法

徐文强，周扬名，王 喆

1.华东理工大学 信息科学与工程学院，上海 200237

2.上海交通大学 中美物流研究院，上海 200030

Li 等人[1]提出的着色旅行商问题（colored traveling salesman problem，CTSP）是一种考虑到工件工作区域部分重合的多旅行商问题（multiple traveling salesman problem，MTSP）。近年来，着色旅行商问题作为一种适于多机差别化访问的问题模型被广泛地拓展和研究。着色旅行商问题是多旅行商问题的扩展，也是具有挑战性的NP难[1]的组合优化问题，当前流行的求解算法多为启发式算法。针对着色旅行商问题模型难以适应现实中存在的冲突条件，本文提出了带冲突图的着色旅行商问题。

作为著名的组合优化问题，TSP 无论是在运筹学、数学还是计算机科学领域均受到持久的关注。TSP 理论已被广泛地应用到各种规划、调度等优化问题，包括计算机电路板布线、印制电路板钻孔、汽配件喷涂等具体案例。而多旅行商问题是对旅行商问题的泛化和发展。在该问题中，一组城市集被多个旅行商访问，且每个城市只允许被旅行商访问一次，最终目标是最小化所有旅行商的总旅行成本。多旅行商问题也已经被广泛应用到各种优化中，例如，人力资源规划、计算机网络的拓扑设计和邮递路线规划等。

在现实生活中，要求城市、配送点或者工作位置在任何条件下均保持开放权限是困难的，也是不现实的。在多旅行商问题的应用中，一些配送点往往只能接受特定的物流供应商供应，一些工件的加工区域往往存在部分重合，事实上双横梁水切割系统问题[1]正是存在上述情况而启发了着色旅行商问题的提出。着色旅行商问题不同于多旅行商问题的显著特点在于着色旅行商问题存在多组城市集，包括各旅行商专属城市集及共享城市集。

而现实中的冲突情况如危险货品运输，对抗条件下的跨境物流，冲突工作位置的多工件协作等具体案例，则进一步推动带冲突图的着色旅行商问题（colored traveling salesman problem with conflicts graph，CTSPCG）的提出。带冲突图的着色旅行商问题需要考虑城市之间的冲突关系。

自Li等人[1]提出着色旅行商问题以来，众多学者不断发展和开拓了相关邻域的研究。孟祥虎[2]对着色旅行商问题进行了泛化研究，提出了包含通用CTSP[2]、串行/连环CTSP[3]和边权重动态CTSP[4]三种问题和相应求解算法。徐向平[5]则在孟祥虎的工作基础上做了进一步拓展，用超图重新描述了孟祥虎提出的三种问题，并提出了双目标CTSP[6]和带有先约束的CTSP[7]以及相应的求解算法。董学士等人则先后提出了着色瓶颈旅行商问题[8-9]、着色平衡旅行商问题[10]和平衡多旅行商问题[11]，以及相应的求解算法。代星[12]和王东明等人[13]则提出了最大值最小化的着色旅行商问题和最大值最小化的连环着色旅行商问题。

着色旅行商问题是多旅行商问题的扩展，也是具有挑战性的NP难[1]的组合优化问题，当前流行的求解算法多为启发式算法。Li 等人[1]提出了遗传算法（genetic algorithm，GA）、贪婪初始化的遗传算法（GA with greedy initialization）、爬坡遗传算法（hill-climbing GA）以及模拟退火遗传算法（simulated annealing GA，SAGA）等算法。Meng 等人[14]提出了变邻域局部搜索算法（variable neighborhood search）。Xu 等人[15]提出了基于德劳内三角的变邻域局部搜索算法（Delaunay-triangulation-based VNS）。He 等人先后提出了迭代两阶段局部搜索算法（iterated two-phase local search，ITPLS）[16]和分组模因搜索算法（grouping memetic search）[17]。韩舒宁等人[18]设计了一种基于均匀设计（uniform design，UD）融合伊藤算法ITÖ和蚁群算法（ant colony optimization，ACO）的混合伊藤算法（hybrid ITÖ algorithm with uniform design，UDHITÖ）。Pandiri 等人[19]提出了蜂群智能方法，Dong 等人[20]则提出了人工蜂群算法（artificial bee colony，ABC）。Zhou等人，即本团队，则先后提出了多邻域模拟退火搜索（multi-neighborhood simulated annealing search）[21]和基于多邻域模拟退火的迭代局部搜索算法（multi-neighborhood simulated annealing-based iterated local search）[22]。

为拓展着色旅行商问题在冲突条件下的适应性，本文参考带冲突图的背包问题[23-24]等冲突条件下的组合优化问题，提出了带冲突的着色旅行商问题。为找到对该问题更好的求解方法，文中所提出的模因算法参考了其他经典的模因算法[25-26]。模因算法能够更好地平衡算法的搜索能力和逃脱局部最优能力。

本文所作的工作如下：

（1）提出了带冲突图的着色旅行商问题（CTSP-CG），建立了相应数学模型，并使用精确算法求解器求解。

（2）提出了基于大领域模拟退火局部搜索的模因算法并求解。比较分析了模因算法和CPLEX精确求解器的实验结果，发现模因算法在20个小规模实例中的9个结果更好，在18 个实例上展现了其远超精确算法的求解速度。比较分析模因算法和其他本文实现的启发式算法，发现模因算法在全部14 个中等规模实例上均取得了更好结果。结果显示模因算法在求解CTSP-CG问题上具有统计学意义的显著性。

（3）通过替换模因算法中的搜索算子进行了消融实验。实验结果验证了模因算法中局部搜索算子的有效性。而通过替换模因算法中的种群更新算子进行的消融实验，则验证了种群更新算子的有效性。

1 带冲突图的着色旅行商问题

图1 是带冲突图的着色旅行商问题的示意图。城市0表示仓库（depot）城市。所有旅行商从城市0出发，最终回到城市0。城市1，2，3 各自分别为旅行商1，2，3的专属城市。专属城市只允许对应旅行商访问。城市4，5，6，7为共享城市。共享城市允许任意旅行商访问，这也意味着城市0即仓库城市也为共享城市。除城市0外，其余城市只能被旅行商访问且仅访问一次。4号城市和5号城市相互存在冲突，因此不允许同一旅行商访问这两个城市。图1 中旅行商1 从0 号城市出发，依次访问了1号专属城市，4号共享城市后回到0号城市；旅行商2 从0 号城市出发，依次访问了3 号专属城市，7 号共享城市，6 号共享城市后回到0 号城市；旅行商3 从0号城市出发，依次访问了2 号专属城市，5 号共享城市，最终回到0号城市。

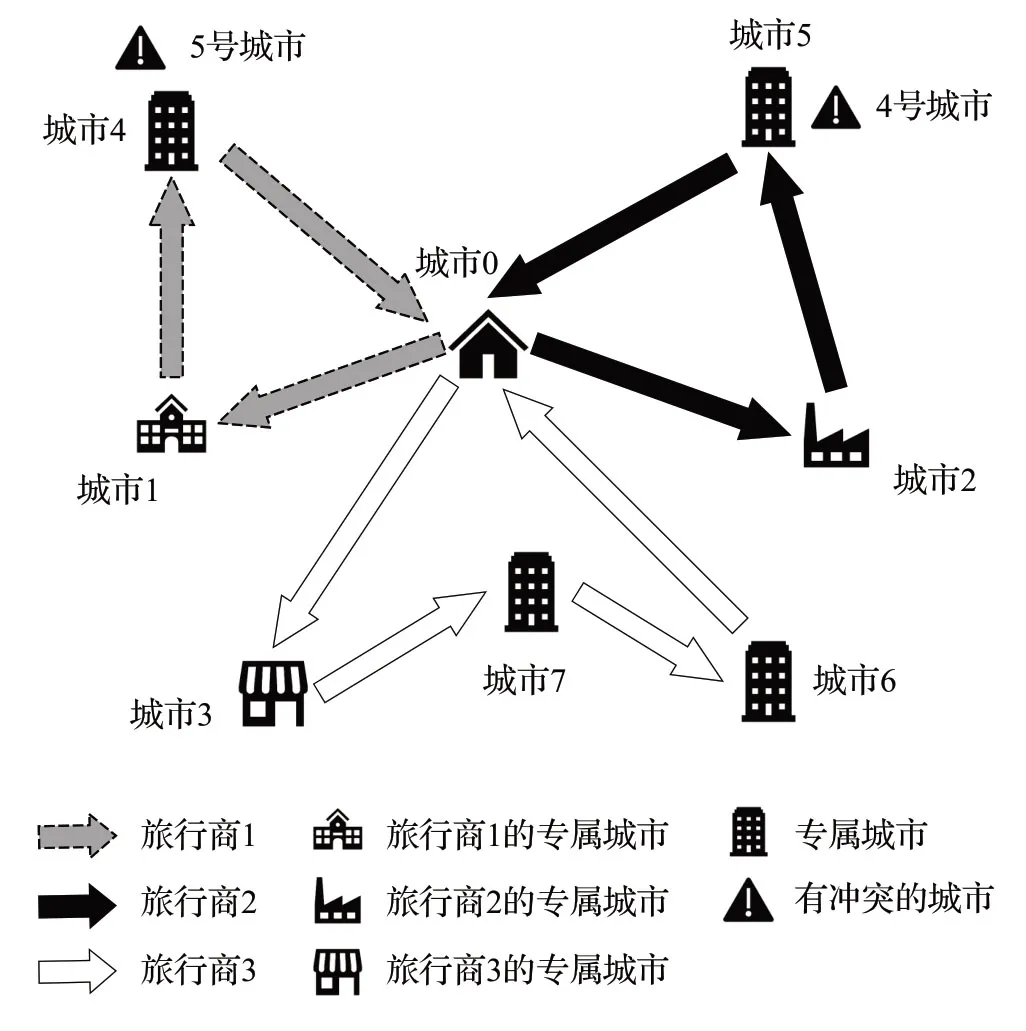
图1 带冲突图的着色旅行商问题示意图Fig.1 Example of colored traveling salesman problems with conflict graph

1.1 问题描述

带冲突图的着色旅行商问题是着色旅行商问题的扩展模型。同着色旅行商问题相似，有m个旅行商和n个城市，其中m，n∈N+，且m＜n。为更好表述该问题，本文引入了一个完全图概念G(V,E)。其中，V表示所有城市的集合，集合大小为n，其中各个城市各自编号为0 到n-1。每条边用(i,j)∈E，i≠j,i,j∈V表示。并且用权重wij表示城市i与城市j之间的距离。V能够被划分为m+1 个非空不相交集合：包含一个共享城市集S和m个旅行商对应的专属城市集C1,C2,…,Ck,…,Cm，其中k表示k号旅行商。数学化表达可以为,Ci∩Cj=φ,∀i≠j∈{0,1,…,m} 。每个专属城市集Ck中的城市只有对应的旅行商k才允许访问，而共享城市集S中的城市可以被任意旅行商访问。除仓库城市外所有城市都必须被访问一次且只能访问一次。访问时，旅行商从仓库城市出发，根据选定的边到下一个城市，访问其对应全部专属城市及选定的共享城市后，最终返回仓库城市，同时规划时也需要确保所有旅行商也访问完了所有共享城市。其中，仓库城市设定为0号城市。

为了适配现实中存在的运输条件冲突情况，带冲突图的着色旅行商问题相对于普通的着色旅行商问题引入了冲突与冲突图H的概念。H为一个n×n的0-1矩阵，当Hij=1 时表示城市i和城市j存在冲突，也即城市i和城市j不允许被同一个旅行商访问。Hij=0则表示没有这样的冲突。该问题的目标与着色旅行商问题的目标相同，即最小化总成本。冲突关系是相互的，因此冲突图矩阵为对称矩阵。

1.2 整数规划模型

不同于3-index整数规划模型[1，16]表示着色旅行商问题。本文采取了2-index的整数规划模型描述带冲突图的着色旅行商问题。其中，决策变量x和y如下：

决策变量xij=1 表示边(i，j)有旅行商通过，若没有旅行商通过，则xij=0。yik也是决策变量，当yik=1时表示旅行商k访问了城市1，若旅行商k未访问，则yik=0。

目标函数为：

问题模型服从下列限制条件：

所有的旅行商只能由0号城市即仓库城市出发，最终也必须返回0号城市，

旅行商k被禁止访问其他旅行商的专属城市，同时其他旅行商也被禁止访问旅行商k的专属城市。也就是说不存在一条这样的边，它由一个专属城市到另一个不同旅行商专属城市构成，

0号城市需由m个旅行商各自访问且仅访问一次：

但这里目前只能表示0 号城市被旅行商总共访问了m次，并不能限制其精确访问一次。要达成上述意图，还需结合以下3个约束。

所有非0 号城市都只由一个城市连入且只连出一个城市：

一个非0号城市只能被一个旅行商城市所访问：

城市与旅行商的一致性约束。不存在相邻两条边被不同旅行商访问，保证决策变量x和y的一致性，进而确保一条路线只有一个旅行商访问，

下式为著名的mtz约束，该约束意在判断图中无子环路，判断方式为除去0 号城市外，剩余规划路线不构成环路。对于CTSP等类MTSP问题而言即便有多个环路，但都必须访问0 号城市，因此该约束仍然生效。此外，mtz约束仅在有向图问题上有效：

当两个共享城市存在冲突时，这两个城市不能由同一个旅行商访问：

2 模因算法

模因算法受文化扩散现象启发，且有机地融合了遗传算法的框架。模因算法并不是内容固定的优化算法，而是作为一种广泛的算法类别和解决特定问题的一般指导方针。模因算法是基于种群的元启发式算法，由一个演化框架和一组局部搜索算法组成，局部搜索算法在演化框架的生成阶段内被使用。模因算法已被广泛地应用于组合优化问题的求解，例如文献[17，25-26]。对于带冲突图的着色旅行商问题，求解算法既要考虑不同城市的可访问性，又要考虑城市之间可能存在的冲突。也就是说相对于着色旅行商问题，带冲突图的着色旅行商问题在原本相对平滑的邻域空间中添加了若干隔断，会导致求解算法在运行时更容易地陷入局部最优解。

本文为降低算法运行时陷入局部最优的概率和提高算法挣脱局部最优的可能，采用了模因算法及自适应大规模邻域搜索算子。同时，更好更快的搜索能力有助于限定时间内找到更好的解，这也是采用自适应大规模领域搜索的另一目的，此外，文中为此采用了贪婪初始化策略。

2.1 解的表示与评估

本文采用的解的表示法为邻接矩阵表示法[16]。其他的表示法包括双基因编码表示法[1]、直接编码表示法[3]。邻接矩阵表示法与直接编码表示法均可以唯二表示一个解，而双基因编码表示法不能。相比于直接编码表示法，邻接矩阵表示法占用的存储空间更大，但插入与删除操作更快更便捷[22]。

以图2 为例，如图所示，左起第一列第二至四行代表旅行商，第一行左起第二至八列代表城市编号。0号城市默认为原点城市。第二行第二列的数字1，代表该位置的列所对应的城市（即0 号城市）在该位置的行所对应的旅行商（即1号旅行商）的下一个城市编号，在这里则为1 号城市。依此类推，可得旅行商1 号的序列为r1：{0，1，4，0}，旅行商2 号的访问序列为r2：{0，2，5，0}，分组3的访问序列为r3：{0，3，7，6，0}。该编码方式克服了双染色体编码方式重复编码多，操作时间复杂度高的问题。是一种相当迅速有效的编码方式。

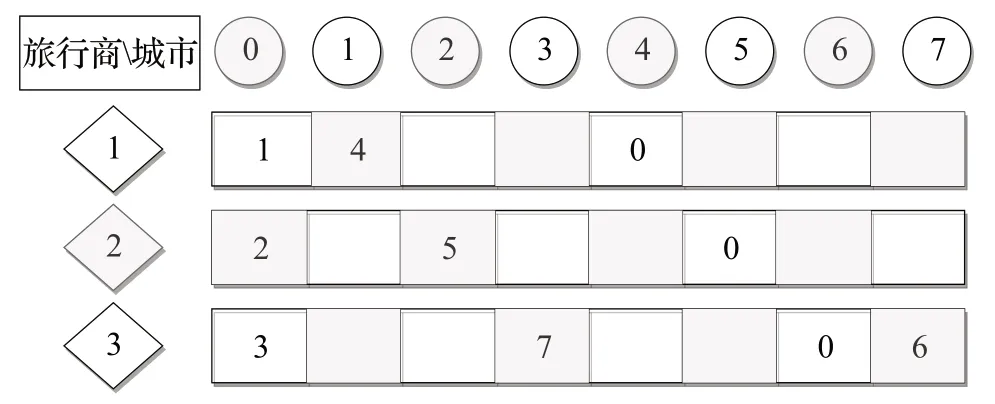
图2 解的表示Fig.2 Presentation of solution

2.2 算法框架

在流程图3中，种群初始化采取了一种贪婪随机方式，以期在算法前期取得较好的结果。选择父本则是完全的随机化的，以提供随机性。交叉算子采用了m-tour方式对解进行重组，以保存父本解的优秀特性。自适应的大规模邻域搜索是该模因算法的核心，作为局部搜索算子获得更好解是有效的。种群更新采取的是简单更新的方式，若新解的结果好于种群中的最坏解，则将新解替换掉种群中的最坏解。

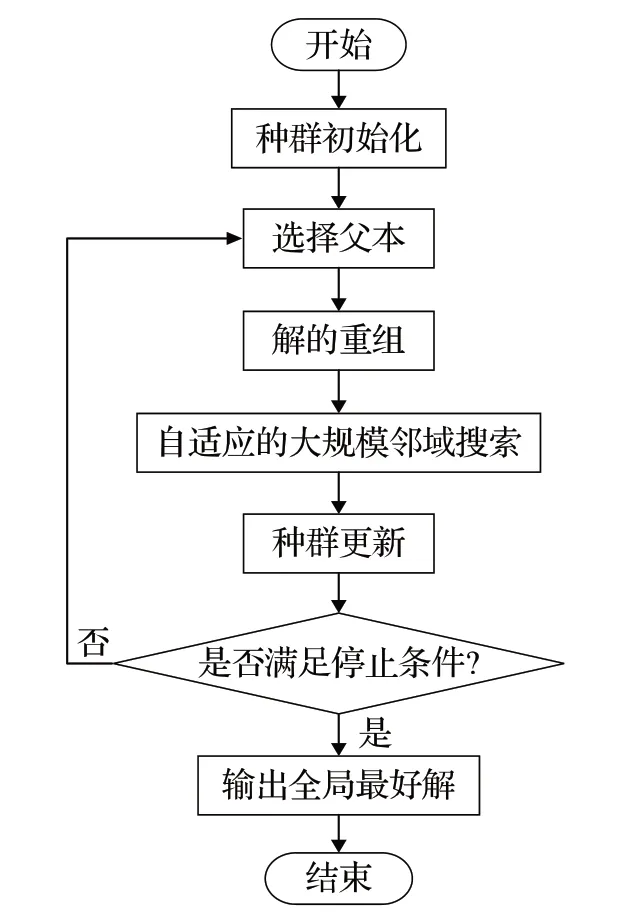
图3 模因算法流程图Fig.3 Flow chart of memetic algorithm

2.3 种群初始化

本文采取了与文献[16-17，19，22]中相似的解初始化方法。带冲突图的着色旅行商问题中包含了共享城市和专属城市两类城市集，因此，为充分利用问题本身的特性，解的初始化方法有两个构造阶段。不同于着色旅行商问题，带冲突图的着色旅行商问题在构造解的过程中需要适应冲突。

种群初始化方法如下：

解的初始化的伪代码

初始化第一阶段为第4～19 行，该阶段将所有专属城市放入了解S中。其中第4行表示遍历所有旅行商，第5 行表示随机选择并遍历旅行商k的专属城市集。第6 行表示初始化Δ，Δ记录了最佳插入位置的代价。第7、8 行表示初始化Index，Index表示找到的最好位置。第9行出现的e(i,j)表示边，该边由i城市出发到j城市，rk表示旅行商k的访问序列。此处需要注意的是，当解S中仅用城市0时，其访问序列为rk：{0，0}，遍历rk所得的边也为e(0,0)。第10～14 行则表示记录最好插入位置和代价。第17行表示将随机遍历的专属城市c插入解中的最好插入位置，根据解的表示其实现可能有所不同。

初始化第二阶段为第21～38行，该阶段将所有的共享城市放入了解S中。其中第21 行表示随机选择并遍历共享城市集U。第22～25 行初始化Δ、Index和BestRoute，BestRoute表示最好位置的旅行商路线。第22 行表示遍历旅行商。第27～29 行判断随机选择的共享城市c是否能插入到旅行商路线rk中而不引起冲突，其具体实现形式与冲突图的实现形式和解的实现形式有关。第30～37行与第9～15行相似，表示找到最好的插入位置，唯一不同的是第35 行额外记录了最好位置对应的旅行商。第39行表示插入共享城市c到解S的最好插入位置。

种群初始化方法则是在解的初始化的基础上初始化多个解。同时，种群初始化在确保种群多样性上也有实际需求，因此需要检测是否有重复解。本文采用判断初始解的值是否完全相同的方式，即，来判断解是否重复。

2.4 自适应的大规模邻域搜索

本文提出的自适应大规模邻域搜索算子包含四个搜索模块，两个更新模块。四个搜索模块分别为：链接重构搜索，路线间邻域搜索，路线内邻域搜索，路线内与路线间联合邻域搜索。两个更新模块分别为：直接更新与模拟退火更新。自适应大规模邻域搜索有多轮迭代。每轮迭代都随机指定一个搜索模块和更新模块，该方式提高了搜索在不同情况的泛用性。四个搜索模块如下：

（1）链接重构搜索受到限制性交叉交换（constrained cross-exchange）[17]启发。该搜索分为两个阶段，链接断开阶段和链接重构阶段。在链接断开阶段需遍历解，然后按概率切出单纯由共享城市组成的链路片段pc。在链接重构阶段，则将随机选定的链路片段pc与各可插入位置e(i,j)进行比较，找出最好的可插入位置及插入方向。这与解的初始化的伪代码中的第22～39 行极为相似，不同处在于需要同k-opt一般额外考虑pc插入到解中的方向是正或逆。若该链路片段pc与所有路线中的共享城市均冲突，则将该链路pc打散成一个个共享城市逐个插入。插入位置的寻找方式和插入方式与第22～39行相同。

（2）路线内邻域搜索与[19，22]中的对应搜索相同。其分为移除阶段和重插入阶段，移除阶段即简单地随机移除解中的专属城市。重插入阶段的工作则与解的初始化第一阶段，即解的初始化的伪代码中的第4～19行相同。

（3）路线间邻域搜索与文献[19，22]中的对应搜索相似。其同样分为移除阶段和重插入阶段，移除阶段随机移除解中的共享城市。重插入阶段的工作则与解的初始化第二阶段，即解的初始化的伪代码中的第21～40行相同。

（4）路线内与路线间联合邻域搜索则是先执行路线间邻域搜索再执行路线内邻域搜索。选择该顺序是受Zhou等人[21-22]在CTSP实例上进行相似实验的启发。

需要注意的是，不同于所参考的求解着色旅行商问题的搜索算子，文中自适应大规模邻域搜索算子的模块必须适应冲突条件。诸模块的适应冲突条件的策略均为规避策略。即比较城市i和路线r1中的城市j∈r1是否满足Hij=1，若满足则认为城市i与路线r1有冲突。为规避冲突，不能把城市i放入路线r1。同理，在模块（1）中若满足Hij=1，其中城市i∈p1属于片段p1，城市j∈r1属于路线r1，则认为片段p1与路线r1冲突。两个更新模块：直接更新即是新结果较好即更新，结果较差则放弃。模拟退火更新则确保接受新的更好解的同时，根据当前温度，按metropolis概率公式判断是否接受新的更差解。当前温度可由当前迭代次数与设定的初始温度换算得出。

2.5 解的重组

解的重组是将选定的多个父本解进行重组，得到一个新的子代解，在遗传算法中通常也可称为交叉（crossover）。图4 是解的重组的示意图。该重组方式为m-tour方式。

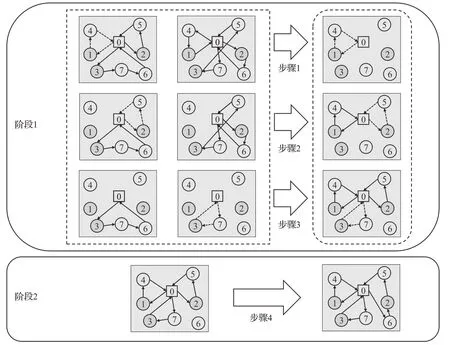
图4 解的重组Fig.4 Reorganization of solution

该重组方案分为两个阶段，在图4所示实例中阶段1有3个步骤，阶段2有1个步骤。图4所示实例所选两个本解于步骤1 左侧表示。左父本解的结构为lr1={0,1,4,0},lr2={0,2,5,0},lr3={0,3,7,6,0} 。右父本解的结构为rr1={0,4,1,0},rr2={0,2,6,0},rr3={0,7,3,5,0} 。其中，1，2，3号城市均为专属城市，5，6，7号城市及0号仓库（depot）城市均为共享城市。

具体如图4中所示。在第一个阶段，找到两个解中每城市代价最小的路线并将其加入新解中，其中每城市代价是通过计算该路线总代价比上该路线城市数得来的。若存在多条每城市代价最小的路线，如步骤1 中lr1={0,1,4,0},rr1={0,4,1,0}，两路线的每城市代价均为最小，则随机一条路线加入到新解中，实例中步骤1选择的是虚线表示的lr1={0,1,4,0} 。加入子代解后，需删去两个父本解中的对应的路线和共享城市，如步骤2 中左右父本解均不存在关于1，4 号的城市的路线，步骤3中右父本解不存在关于2，5，6号城市的路线。重复以上操作，直到所有路线都被构建，也即专属城市全部加入解中。

在第二阶段，需要重新插入第一阶段完成后剩余的未加入到解中的共享城市，图4 中所示实例仅有6 号城市未插入到解中，因此仅需一个步骤，步骤流程与解的初始化第二阶段相同。具体到图4 实例而言，6 号城市先对步骤4中左侧原解中的每条路线所属的旅行商进行考察，判断是否存在冲突；之后，对不存在冲突的旅行商的边进行考察，找到增加的成本最小的边，如e(0,2)后，将城市插入该边，即删除e(0,2)，增加e(0,6)，e(6,2) 。

2.6 种群更新

当前对种群进行更新的策略有多种，从替换的解可分为：替换最坏解[1，17]，替换当前位置解[10-11,18-20]。从更新的评估公式可分为：考虑多样性[1，17]，不考虑多样性[10-11，18-20]。从接受的策略可分为：无论新解优劣直接接受[10-11，18]，新解更优才接受[1，17]，按概率接受更新[19-20]。这些种群更新的策略应用在不同的基于种群的算法上。

本文采取的更新策略为，替换最坏解且考虑多样性的新解更优才接受的方式。其对多样性的评估方式是观察原种群中是否有与新解相同的解。当一个新解生成后，判断其是否已在种群中，若存在则说明多样性不足，将其放弃。否则继续判断其是否比当前最坏解更坏，若更坏则放弃。否则，将其替换掉最坏解。

2.7 算法时间复杂度分析

在循环开始后，需要执行选择父本组件，由于本文中该组件是完全随机化的，因此，可认为其复杂度为O(1)。之后需要执行解的重组组件，其第一阶段时间复杂度为O(n)，第二阶段的时间复杂度为O(pres·n2)，其中pres表示第一阶段剩下的城市的概率，解的重组整体的时间复杂度为O(pres·n2)。自适应大规模邻域搜索算子包含四个搜索模块和两个更新模块，四个搜索模块在具体运行中的花费或有不同，但时间复杂度均可用O(pc·n2)表示。其中pc为城市被选中而重新插入到解种的概率。因此，单次循环的时间复杂度可以表示为O((pres+pc)·n2)，或者将pres和pc视为常数，用O(n2)表示。

3 实验与结果分析

3.1 基准实例

本文采取的实验实例如表1所示。其中，eil来自于文献[1]，gr来自于文献[19-20]。这些数据由原始的TSP数据转换而成，原始名为TSPLIB，可从以下网址下载：http：//people.sc.fsu.edu/～jburkardt/datasets/tsp/tsp.html。此外，冲突图由限制联通子图的算法随机生成，以确保其必定有解。

表1 实验中使用的CTSP-CG实例Table 1 Instances of CTSP-CG used in experiments

3.2 实验设置

本文所采取的实验环境为：AMD Ryzen 7 5800H with Radeon Graphics，3.20 GHz处理器和16 GB RAM。本文提供了一个精确算法和两个启发式算法均采用C++语言，且均使用MSVC 2019 在Windows 系统上编译后运行。

本文在小规模实例上运用CPLEX算法软件进行了精确算法的实验，以求得实例解目标值的可靠范围。本文提出并实现了一个基于大规模邻域模拟退火搜索的模因算法在小规模实例及中等规模实例上运行，以进一步优化实例解。最后，本文设计并实现了一个消融实验：通过用单纯的链接重构搜索算子替换模因算法中的局部搜索算子得到了一个新的启发式算法，在部分小规模及中大规模实例上运行，并与原模因算法对比分析。

模因算法的种群大小为20，一般遗传算法或模因算法的所取大小为20～40[1，3，17，25-26]，大规模的种群可以提高搜索范围，但也会增大初始化种群的开销。自适应大规模领域局部搜索算子的初始温度为1 000，最大迭代次数为400，降温速率为0.97，上述参数设置参考文献[22]，文献中给出了多组参数配置，文中采用了给出的推荐配置之一。初始温度和降温速率过大会导致退火过程无法收敛，反之则可能导致退火过程收敛过快。最大迭代次数越大，搜索效果越好，但开销也相应增加。链接重构搜索算子中切出的链路片段的最大长度为7，该参数设置参考文献[17]精确算法在小规模实例上的设定截止时间为7 200 s。链路片段过大会导致片段过于完整趋近于路线，链路片段过小会导致其碎片化趋近于单个城市，都会失去链路重构的意义。启发式算法在小规模实例上的运行时间为60 s，中等规模实例的运行时间为600 s，所有实例均运行10次。eil51-3和eil101-5实例中的城市数比常规实例多出2个，是为了更好地适配算法输入输出的数据结构，重复了专属城市两次，这对于最优解值是无影响的，但是提高了找到最优解的难度。

3.3 实验结果分析

表2 是精确算法与启发式算法在CTSP-CG 小规模实例上的求解结果比较。表2 左侧CLEPX 栏中显示，在eil21-2 到eil41-3 及eil51-2 等8 个实例，CPLEX 均能获得有效结果，用时均少于7 200 s，其上界与下界间隔极小，对于最小化问题，可以认为其上界结果是真实值。精确式算法在实例eil51-4 和eil51-4 到eil101-6 上均超过运行时间7 200 s，并未确定最好解。超过7 200 s的实例中，仅有eil41-4，eil51-3 和eil51-5 三个实例的上界与启发式算法所得到的最好解和平均解匹配。

表2 小规模实例上的实验结果对比Table 2 Comparisons of results on small scale instances

表2右侧ALNMEM栏显示，在全部小规模实例上，本文提出的模因算法均得到了稳定的最好解。从运行时间上看，模因式算法的效果在所有实例上的运行时间均少于精确式算法。从运行结果上看，模因算法在9个实例上超过精确式算法，其余实例与精确式算法的上界匹配。表2中比较了精确式算法下界和模因算法的平均秩次，发现模因算法的平均秩次小于精确算法的平均秩次。平均秩次是比较多实例多组数据的一种度量方式。平均秩次计算方式为比较多组数据之间实例相同的数据并排名，从1开始，数据值越小则排名序号越小，若某实例有多组数据排名相同则将排名取平均，例如有两组数据并列第一则两组数据排名均为1.5，最后按组别将每个实例数据相加并除以实例数。平均秩次越小则说明该组数据结果越佳。经wilcoxon符号秩检验分析[27]，分别比较ALNMEM的平均解和最好解与CPLEX的下界，其p值均为0.003 9，小于0.05，具备统计学意义的显著性。

表3 是启发式算法在CTSP-CG 中等规模实例上的求解结果比较。中等规模的CTSP-CG 实例共有14 个。表3中基于均匀设计的混合伊藤算法（UDHITÖ）源于文献[18]，人工蜂群算法（ABC）源于文献[20]，迭代两阶段局部搜索（ITPLS）源于文献[16]。此外，文中根据CTSP-CG的问题特性对两个算法进行了一定修改。对于UDHITÖ 算法、ABC 算法和ITPLS，在原算法的基础上增加了初始化和搜索时的限制措施，使得该算法初始化和搜索邻域的得到的解均为无冲突的合法解，得到了新的算法ABC*。此外，文中统一将算法的停止条件设置为600 s截止。

表3 中等规模实例上的实验结果对比Table 3 Comparisons of results on medium scale instances of CTSP-CG

UDHITÖ 的使用蚁群算法初始化的时间复杂度为O(n2)，UDHITÖ内部有两个循环结构，其中一个小循环结构嵌套在一个大循环结构中。小循环结构的时间复杂度为O(popSize·n2)。小循环结构在大循环结构中的停止条件为最大未改进次数，其值参考文献[18]设为60。ABC 初始化需要依次生成路线内和路线间邻域解，其时间复杂度可综合为O(n2)，而一轮迭代的时间复杂度为O(popSize·n2)。ITPLS 采用2-opt 和re-insert作为搜索算子，其时间复杂度均为O(n2)，此外ITPLS也有两个循环结构，小循环结构的停止条件为50次[16]。

表3 显示，模因算法能够在精确式算法难以求解的中等规模实例上取得较好解，且相对于其他启发式算法，模因算法在中等规模实例上的求解结果均较好。经wilcoxon 符号秩检验分析[27]，无论最好解或平均解，ALNMEM 与另外三个算法分别比较的p值均为1.22E-4，小于0.05，具备统计学意义的显著性。而比较平均秩次后，可以认为ANLMEM相对其他启发式算法在平均解和最好解上均具有优势。

新模因算法ALNMEM*与原模因算法ALNMEM在部分实例下的对比结果如表4 所示。可以看出仅在实例eil76-5 上两算法均稳定取得匹配的最好解和平均解。而在实例eil101-7上，两算法得到了相同的最好解，但ALNMEM的平均解好于ALNMEM*。而在其他实例上，ALNMEM 的最好解与平均解均好于ALNMEM*。平均秩次也表明，无论在平均解还是最好解上ALNMEM相对ALNMEM*均具有优势。

表4 不同搜索算子的模因算法的实验结果对比Table 4 Comparisons of memetic algorithms with different searching operation

表5中ALNMEM**是更换ALNMEM中的种群替换策略所得到的新算法。具体而言，是将原种群替换策略中的“考虑多样性”替换为“不考虑多样性”，即不进行检测新解与原解是否重复，只要新解比种群中的最坏解好，就用新解替换掉种群中的最坏解。可以看出，在实例eil76-5 和eil101-7 上两算法均取得了匹配的最好解和平均解。而在实例gr229-30，gr666-15 上，原算法ALNMEM 在平均解和最好解上均好于新算法ALNMEM**。平均秩次同样表明，ANLMEM 相对ALNMEM**在平均解和最有解上均占有优势。

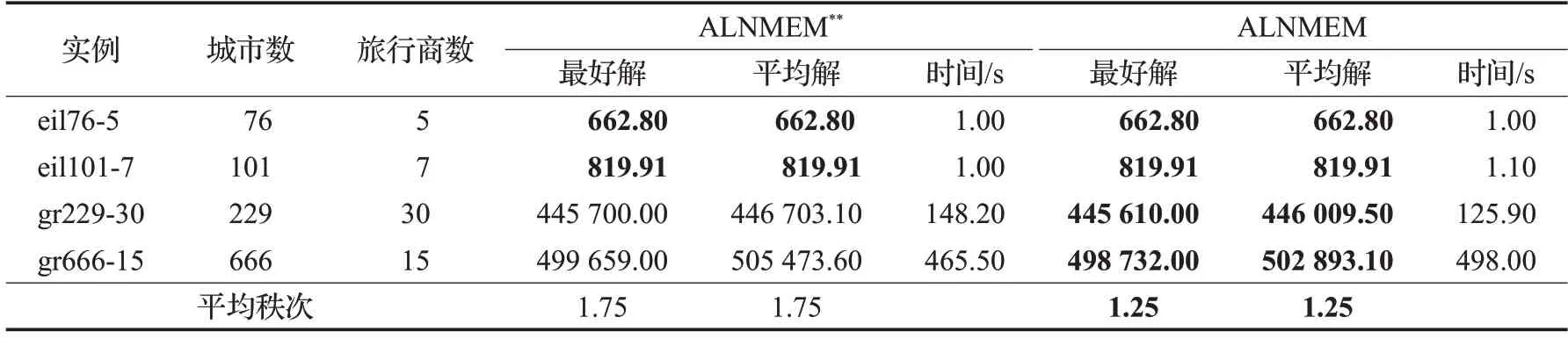
表5 不同替换策略的模因算法的实验结果对比Table 5 Comparisons of memetic algorithms with different replace strategy

4 结语

针对着色旅行商问题难以有效处理具有冲突的应用场景，本文首次提出了一个考虑冲突图的着色旅行商问题。本文首先构建了带冲突图的着色旅行商问题的整数规划模型，使用了CPLEX 软件进行了求解。为了处理更大规模的问题实例，本文提出并实现了一个有效的模因算法。与精确算法对比，本文所提出的模因算法展示了优越的性能。

后续工作可聚焦于：（1）将本文所提模因算法应用于更多乃至极端状况下的真实情景。（2）进一步提高本文所提模因算法的自适应能力，从而更稳定快速地求解。