观测不确定性下的高效贝叶斯更新方法及其在机翼结构中的应用

于汀，李璐祎，刘昱杉，常泽明

西北工业大学 航空学院，西安 710072

20 世纪60 年代初，贝叶斯模型更新开始受到结构工程师的广泛关注，最早被用于土木工程结构分析和鉴定，后来被广泛应用于结构系统健康监测、模型校正、可靠性评估等领域［1］。贝叶斯模型更新是一种基于先验信息和观测数据校准模型的有效方法，其主要目的是结合代表工程师经验判断的先验分布和代表观测数据的似然函数，利用贝叶斯概率公理［2］，得到模型参数的后验分布，从而减小模型的不确定性。设原系统模型输入变量为X，则根据贝叶斯理论可以得到输入变量X的后验分布［3］为

式中：x为输入变量X的样本；s为观测数据；fX(x|s)、fX(x)分别为输入变量X的后验和先验分布密度函数；L(X|s)为似然函数。从式（1）中可以看出fX(x|s)的计算需要求解分母中的n重积分，通常难以求得解析解，因此人们研究并发展了大量求解该式的近似解法。文献［4］首先采用Laplace 方法给出了积分的近似解，但是这种方法只适用于后验分布概率密度函数在几个孤立点处存在峰值的情况。近年来，随着计算机性能的飞速发展，大量基于随机过程模拟的抽样方法被用来进行贝叶斯模型更新中后验样本分布的估计，其中发展迅猛且最为有效的是马尔科夫链蒙特卡洛（Markov Chain Monte Carlo，MCMC）方法［5］。MCMC 方法通过模拟稳态分布为目标后验分布的马尔科夫链，来产生一组满足后验分布的相关样本，从而利用样本估计后验统计信息。在MCMC 方法的基础上，Beck 和Au［6］基于“ 拒绝采样”思想提出Adaptive-Metropolis-Hastings 方法（AMH），采用核密度估计通过中间过程概率密度函数逐步逼近真实的后验样本的概率密度函数。对于高维问题，上述AMH 算法通常会得到大量重复样本，抽样效率很低。为了提高AMH 算法对高维问题的适用性，研究者相继提出了过渡马尔科夫链蒙特卡洛方法（Transitional Markov Chain Monte Carlo，TMCMC）［7］、混合蒙特卡洛方法（Hamiltonian Monte Carlo，HMC）［8］等有效地改善了AMH 算法对高维问题的适用性。然而，上述基于MCMC 发展的方法通常很难判断何时马尔可夫链已经渐进收敛于平稳分布且计算量较大［9-11］，因此一些学者提出了用于替代MCMC 的方法，如序列粒子滤波［12］、贝叶斯网络框架（Bayesian Network，BN）［13］、贝叶斯近似计算（Approximate Bayesian Computation，ABC）［14］等方法，其中，Straub 和Papaioannou［15］于2015年提出了一种基于结构可靠性方法的贝叶斯模型更新（Bayesian Updating with structural Reliability，BUS）方法，这种方法基于简单拒绝抽样的思想，建立了贝叶斯更新与结构可靠度之间的桥梁，有效地将复杂贝叶斯更新中的高维积分问题转化为一个典型的结构可靠性分析问题，进而采用可靠性分析方法来求解后验样本的分布，为贝叶斯模型更新问题开辟了一条新的求解思路。

然而，上述已有的方法都是在假设似然函数中的观测值是准确测量的情况下进行的，即只考虑了输入变量及其参数的不确定性。在工程实际获取试验数据的过程中，由于测量仪器的精度误差，以及一些不可避免的人为因素带来的误差，导致观测值不能准确测得，即观测值也具有不确定性。确定性观测值下贝叶斯模型更新的后验分布参数是确定的，如后验均值和后验方差；而不确定性观测值会导致贝叶斯更新输出的后验分布参数也具有不确定性，因此为了准确获取后验样本的完整分布，就必须考虑观测值在整个不确定性范围内对贝叶斯模型更新后验样本分布的影响。文献［16］基于MCMC 方法提出了一种观测不确定性情况下的贝叶斯更新方法，但计算量比较大，而且MCMC 方法无法确保最终收敛到稳态分布。因此，本文基于BUS 方法建立观测不确定性下的贝叶斯更新模型，充分考虑观测值在整个不确定性范围内对贝叶斯更新后验样本分布参数的影响，并提出单层Kriging、双层Kriging 2 种模型求解的高效算法。

1 观测不确定性下的贝叶斯更新

1.1 BUS 方法基本原理

考虑结构模型Y=g(X)，其中X=(X1，X2，…，Xn)为n维随机输入变量，如尺寸、材料性能、载荷等，其先验分布为fX(x)；Y为模型输出，如应力、应变、位移等；g(·)为输入和输出关系的模型。假设通过试验或者测量得到输出的一组观测数据s=(s1，s2，…，sm)，在观测数据s下输入变量X的似然函数记为L(X|s)，其中第i个观测值下的似然函数通常表示为第i个观测值与模型输出之间的偏差的概率密度函数［3］，即

为了解决式（1）中n重积分难以求解的问题，BUS 方法通过引入一个定义在［0，1］区间上均匀分布的辅助变量P，利用简单拒绝抽样方法来得到满足后验分布的样本，从而将贝叶斯更新问题转化为结构可靠性问题。将引入辅助变量P之后的增广变量空间记为[X，P]，且增广变量的联合密度函数满足fX，P(x，p)=fX(x)fP(p)，其中p为辅助变量P的样本。为建立贝叶斯更新和结构可靠性分析之间的关系，定义新的失效区域Ω为

式中：c为一个和似然函数相关的正常数，使得对于任意的输入变量X都有cL(X|s)≤1。基于式（3），可以得到一个可靠性问题的极限状态方程：

因此，在BUS 方法中可得到后验分布表达式［15］为

式中：I为指示函数，当h(X，P)≤0 时，I=1，反之，I=0。由式（5）可知，由先验分布fX(x)产生且落入失效区域Ω中的样本x将服从于后验分布fX(x|s)。关于式（5）的详细推导可参照文献［15］。

由此可见，BUS 方法只需确定一个与似然函数相关的参数c，便可有效地将贝叶斯更新问题转化为结构可靠性分析问题，从而使得常用的可靠性分析方法都可以用来进行贝叶斯更新，有效避免贝叶斯模型更新过程中高维积分难以求解的问题，因此，本文将BUS 方法进一步推广到不精确观测的情况。

1.2 观测不确定性下的贝叶斯更新模型

观测误差是模型更新问题中最主要的不确定性因素之一，在结构的监测过程中，仪器精度、环境干扰等不确定性因素都会造成观测数据失真，观测误差的存在导致似然函数存在不精确性，使得贝叶斯更新更加复杂。为此，本文借鉴BUS 方法，建立考虑观测不确定性的贝叶斯更新模型。假设试验中测量得到的m个输出响应的观测数据为s0=[s1，s2，…，sm]，由于环境因素，测量仪器精度等导致的相应的测量误差为δ=[δ1，δ2，…，δm]，则真实的观测数据S=[S1，S2，…Sm]将具有不确定性，并且存在于观测数据与测量误差组成的区间中，即Si∈[s0-δi，s0+δi] (i=1，2，…，m)。令则在观测不确定性和输入变量的随机不确定性共同作用下第i个观测的似然函数可以抽象为一个区间函数：

借助于BUS 方法的思想，引入一个定义在区间[0，1]上均匀分布的辅助变量P，则可将观测区间不确定性和基本变量随机不确定性共同作用下的贝叶斯更新问题转化为区间和随机变量共同作用下的可靠性分析问题。由于区间不确定性和随机不确定性的共同作用，该可靠性分析问题的功能函数则为

式中：c1、c2为一组与似然函数相关的正常数，使得对于任意的输入变量X都有而相应于式（8）中功能函数的失效域也不再单一，而是具有上下2 个边界，即

以功能函数中含有2 个观测变量为例，考虑观测不确定性下的结构的功能函数及失效域如图1 所示。

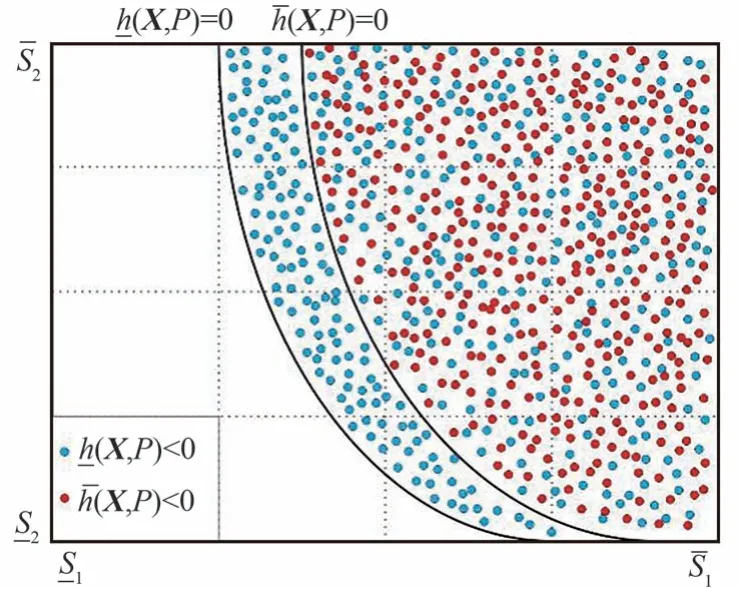
图1 二维独立观测变量下功能函数及失效样本分布Fig.1 Performance functions and corresponding failure domains in case of two-dimensional independent observation variables

基于此，可得到后验分布的区间函数表示为

由式（7）～式（10）可知，本文借助于BUS 的思想，可以将观测不确定性下的贝叶斯更新问题转化为区间和随机变量共同作用下的可靠性分析问题，进而建立观测不确定性下的贝叶斯更新模型。所建模型表明，当考虑观测不确定性时，输入变量的后验分布不再是单一的分布函数，而是一个区间函数，直接准确求解式（10）中的后验分布区间函数通常需要大量的计算量。为了提高观测不确定性下贝叶斯更新的效率，本文将建立观测不确定性下贝叶斯更新的两类基于Kriging 代理模型的算法。为了便于理解，第2 节简单介绍Kriging 代理模型及建模方法。

2 Kriging 代理模型及建模方法

2.1 Kriging 代理模型的基本原理

Kriging 最初由南非采矿工程师Krige［17］于20 世纪50 年代提出，近年来发展为一类流行的统计学插值方法。作为一种插值模型，Kriging 预测结果为所有样本点处模型响应的线性加权，且权重取决于训练样本点与预测样本点之间的空间距离。相比于其他代理模型，Kriging 不仅能给出预测值，还能提供预测方差来衡量模型本身预测不确定性［18］。Kriging 模型可以表示为随机分布函数和多项式之和［19］：

式中：gK(X)为未知的Kriging 模型；φT(X)=[φ1(X)，φ2(X)，…，φp(X)]为n维随机向量X的回归基函数；p为基函数的个数；β=[β1，β2，…，βp]T为基函数的最小二乘回归系数；φT(X)β为由基函数组成的线性回归项，代表随机过程中均值的偏移，用来拟合模型的整体趋势；Z(X)为均值为0、方差为σ2的高斯过程，其协方差矩阵表示为

式中：σ2为高斯过程方差；R(x(i)，x(j))为任意2 个输入样本之间的相关函数，其为相关矩阵R的分量，i，j=1，2，…，m0；m0为训练样本集中数据个数。R(x(i)，x(j))在大多数工程问题中都采用高斯型相关函数，计算公式为

由广义最小二乘回归方法可以得到Kriging模型在未知点x处的预测值gK(x)为

最优相关参数d=[d1，d2，…，dn]T可通过求极大似然估计的最大值得到，即

2.2 交叉验证方法

假设K折交叉验证中，初始训练样本集D{x，y} 由M个输入输出对 (x(i)，y(i)) (i=1，2，…，M)组成，其中y(i)为训练样本点x(i)的响应值。首先将D分成K个大小相似的互斥子集，即，然后，使用K-1 个子样本集构造Kriging 代理模型，剩余的子样本集作为测试样本用来计算代理模型的误差，将该过程重复K次，直到每个子样本集都被作为测试样本使用过一次。由此得到K×1 交叉验证误差向量ecv和K×1 预测方差向量可分别表示为

图2 10 折交叉验证示意图［21］Fig.2 Schematic diagram of 10-fold cross validation［21］

通过交叉验证方法，均方根误差的计算公式为

误差相关系数为

3 考虑观测不确定性的贝叶斯更新算法

BUS 方法的有效性依赖于正常数c的选取，c的取值需要使得任意的先验分布样本都满足cL(X|S)≤1。因此c的最优值定义为1/max(L(X|S))［3］。一方面，c取值过大会导致由简单拒绝抽样得到的样本并不全满足后验分布，降低了BUS 方法的准确性；另一方面，c取值过小将会导致得到满足后验分布的后验样本很少，降低了BUS 方法的计算效率。因此BUS 方法的关键在于常数c的确定，但是对于大多数似然函数，特别是存在多个观测值的贝叶斯更新问题，c的值通常无法解析计算，而数值计算c的过程中需要大量调用原始模型。当考虑观测不确定性时，需要在不同观测值处重复计算常数c，这一过程需要大量调用原始模型，对于大型复杂结构有限元模型计算成本巨大，观测不确定性下的贝叶斯模型更新带来了新的挑战。因此，本文引入Kriging 模型，建立求解观测不确定性下贝叶斯更新模型的单层Kriging 和双层Kriging 算法，有效地提高观测不确定性下贝叶斯模型更新的计算效率。

3.1 双层Kriging 算法

双层Kriging 算法的基本思想是借助似然函数中观测区间不确定性与基本变量随机不确定性可以分离的特点，建立原始模型的带交叉验证的Kriging 模型，并代入原似然函数得到代理似然函数。然后基于代理似然函数，通过历遍观测变量取值区间的方法，得到式（7）中的区间似然函数与式（8）中的区间功能函数的上下边界，并结合Monte Carlo 模拟（MCS）方法求解式（10）得到相应的后验分布区间，具体的计算步骤如下。

步骤1将n维输入变量X增广为n+1 维X+=[X，P]，并根据X的联合概率密度函数fX(x)产生X+前n维容量为N的样本池Q={x(1)，x(2)，…，x(N)}，作为更新Kriging 代理模型和贝叶斯更新的样本池；1 维辅助变量P的容量为N的样本池P={p(1)，p(2)，…，p(N)}由［0，1］区间上的均匀分布概率密度函数随机产生。

步骤2在样本池Q中抽取前M（M≪N）个样本x(o)(o=1，2，…，M)，代入原模型g(X)，计算相应的功能函数值g(x(o))(o=1，2，…，M)，由这M个输入输出样本对构成初始训练样本集D={(x(1)，g(x(1)))，(x(2)，g(x(2)))，…，(x(M)，g(x(M)))}。

步骤3将D分成大致相等的K份子样本集，然后使用K-1 个子样本集构造原始功能函数的Kriging 代理模型，剩余的子样本集作为测试样本用来计算代理模型的误差，将该过程重复K次，直到每个样本集都被作为测试样本使用过1 次，由此得到交叉验证的误差向量ecv。

步骤4根据式（22）计算交叉验证的均方根误差RMSEcv，当RMSEcv≤0.05 时停止交叉验证过程，执行步骤6。若RMSEcv＞0.05，则需在训练样本集D中继续增加Kriging 建模输入输出样本对，执行步骤5。

步骤5在样本池Q中抽取第M+1 至第M+M/K个样本，M+2，…，M+M/K)，计算相应的功能函数值构成补充训练样本集将补充训练样本集D+并入训练样本集D，即M+M/K，再令M=M1，返回步骤3 更新Kriging模型。

步骤6采用当前Kriging 模型gK(X)替代原模型g(X)，得到代理似然函数L(X|S)=

步骤7在观测区间[s0-δi，s0+δi] (i=1，2，…，m)上由均匀分布概率密度函数随机产生m维容量为l的观测样本池S={s(1)，s(2)，…，s(l)}，作为构建区间似然函数的观测值样本池。

步骤8将观测样本池S中的第j(j=1，2，…，l)个观测样本和样本池Q中变量X的N个样本Q={x(1)，x(2)，…，x(N)}代入代理似然函数，计算得到第j个观测样本对应的N个代理似然函数值并求得代理似然函数的最大值，取cj=1/max(L(x(r)|s(j))) (r=1，2，…，N)。

步骤9将步骤8中得到的N个代理似然函数值和增广变量X+的第n+1维辅助变量P的N个样本P={p(1)，p(2)，…，p(N)}一起代入极限状态方程hj(X，P)=P-cj L(X|S)，计算得到第j个观测样本对应的N个极限状态函数值hj(x(r)，p(r))(r=1，2，…，N)，求得满足hj(x(r)，p(r))≤0(r=1，2，…，N)的所有后验样本并计算后验样本的均值和标准差

步骤10若j＜l则令j=j+1，返回步骤8，从观测值样本池S中抽取下一个观测样本，计算新的观测样本下的后验分布；若j≥l则结束贝叶斯更新，执行步骤11。

步骤11将求得的l组后验样本的均值及标准差按次序统计量排序，取得其最大值和最小值作为最终后验样本分布参数的区间端点，即后验样本均值标准差

双层Kriging 算法通过外层历遍观测区间和内层构建原始功能函数的代理模型的方式，可以精确地给出后验分布参数的取值区间，适用于对后验分布参数精度要求较高的观测不确定性下的贝叶斯模型更新问题。但其由于采用双层计算框架，一般计算量较大，计算效率不高。在观测不确定性下的贝叶斯更新过程中，有时不需要很精确地得到后验样本分布参数的区间，而只需要求得后验分布参数的平均估计即可对原模型进行校正，为此，本文建立了带交叉验证的单层Kriging 算法。

3.2 单层Kriging 算法

单层Kriging 算法的基本思想是将观测变量看作观测区间中的均匀分布变量，进而直接建立反映似然函数与观测变量和基本随机变量之间关系的带交叉验证的Kriging 模型。然后基于代理似然函数，结合MCS 方法得到相应的平均后验分布，具体的计算步骤如下。

步骤1将n维输入变量X增广为n+1+m维X+=[X，P，S]，并根据X的联合概率密度函数随机产生n维输入变量X的容量为N的样本池Q={x(1)，x(2)，…，x(N)}，Q作为更新Kriging 代理模型和贝叶斯更新的样本池；1 维辅助变量P的容量为N的样本池P={p(1)，p(2)，…，p(N)}由区间［0，1］上的均匀分布概率密度函数随机产生；m维观测变量S的容量为N的样本池S={s(1)，s(2)，…，s(N)}由观测区间[s0-δi，s0+δi](i=1，2，…，m)上均匀分布概率密度函数随机产生，S作为构建似然函数的观测值样本池。

步骤2在样本池Q中抽取前M（M≪N）个样本x(o)(o=1，2，…，M)，代入原模型g(X)，计算得到相应的功能函数值g(x(o))(o=1，2，…，M)；在观测样本池S中抽取前M个观测样本s(o)(o=1，2，…，M)。将g(x(o))(o=1，2，…，M)、s(o)(o=1，2，…，M)代入似然函数，计算相应的似然函数值将M对输入样本(x(o)，s(o))(o=1，2，…，M) 和输出样本L(x(o)|s(o))(o=1，2，…，M)构成初始训练样本集

步骤3将D分成大致相等的K份子样本集，然后使用K-1 个子样本集构造似然函数的Kriging 代理模型，剩余的子样本集作为测试样本用来计算代理模型的误差，将该过程重复K次，直到每个样本集都被作为测试样本使用过1 次，由此得到交叉验证的误差向量ecv。

步骤4根据式（22）计算交叉验证的均方根误差RMSEcv，当RMSEcv≤0.05 时停止交叉验证过程，执行步骤6。若RMSEcv＞0.05，则需在集合D中继续增加Kriging 建模输入输出样本对，执行步骤5。

步骤5在样本池Q中抽取第M+1 至第M+M/K个样本x(o+)(o+=M+1，M+2，…，M+M/K)，计算相应的功能函数值g(x(o+))(o+=M+1，M+2，…，M+K)；在观测样本池S中抽取第M+1 至第M+M/K个观测样本s(o+)(o+=M+1，M+2，…，M+M/K)，将功能函数值和观测样本代入似然函数计算相应的似然函数值(o+=M+1，M+2，…，M+M/K)构成补充训练样本集将补充训练样本集D+并入训练样本集D，即D=D+D+={(x(o)，L(x(o)|s(o)))} (o=1，2，…，M+M/K)，令M1=M+M/K，再令M=M1，返回到步骤3 更新Kriging 模型。

步骤6采用当前Kriging 模型替代原似然函数L(X|S)，得到代理似然函数LK(X|S)。

步骤7将输入变量X的N个样本Q={x(1)，x(2)，…，x(N)}及观测变量S的N个样本S={s(1)，s(2)，…，s(N)}代入代理似然函数LK(X|S)，计算得到N个代理似然函数值LK(x(r)|s(r))(r=1，2，…，N)，并求得代理似然函数的最大值，取

步骤8将辅助变量P的N个样本P={p(1)，p(2)，…，p(N)}、步骤7 中得到的N个代理似然函数值LK(x(r)|s(r))(r=1，2，…，N)、常数c代入极限状态方程h(X，P)=P-cL(X|S)，计算得到N个观测样本对应的极限状态函数值h(x(r)，p(r))(r=1，2，…，N)，求得满足h(x(r)，p(r))≤0(r=1，2，…，N)的所有后验样本xh，并计算后验样本xh的均值μh和标准差σh。

单层Kriging 算法通过将观测变量看作观测区间中均匀分布的随机变量，进而直接建立起似然函数与观测变量和基本随机变量的Kriging 代理模型，可以给出后验分布参数的平均估计，计算效率较高，适用于对后验分布参数精度要求不高的观测不确定性下的贝叶斯更新问题。

4 算例

本节用3 个观测不确定性下的贝叶斯模型更新问题，验证本文所建观测不确定性下的贝叶斯更新模型对于降低输入变量分布参数不确定性的有效性，以及所提2 种算法对于后验样本分布参数计算的准确性和高效性。对于每个算例，本文采用直接的MCS 方法作为对比参考方法，通过将各算法执行30 次运算得到后验方差的变异系数来判断算法是否收敛。

4.1 一维线性数值模型

算例4.1 采用一个具有解析后验分布的例子来验证本文方法的准确性和可靠性。考虑一维线性数值模型g(X)=X，其中X的先验分布fX(x)是均值为μ、标准差为σ的正态分布，似然函数L(X|s)是均值为S、标准差为σε的正态分布，先验概率分布和似然函数之间满足共轭关系。在这种情况下，X的后验概率分布仍为正态分布，并且具有解析表达式。假设可以得到变量X的ns组观测数据si，则X的后验均值μh和标准差σh的解析表达式［22］为

在本算例中，考虑X的5组观测数据分别为0.5、0.6、-0.4、0.3、0.2，观测误差均为0.05，故观测变量：S1∈[0.45，0.55]、S2∈[0.55，0.65]、S3∈[-0.45，-0.35]、S4∈[0.25，0.35]、S5∈[0.15，0.25]。因此本例的似然函数表示为

式中：σε为试验中观测误差的标准差，取σε=1。本例输入变量的先验分布取为标准正态分布，即X～N(0，1)。利用上述似然函数可以对输入变量进行贝叶斯更新。

本算例需更新线性系统的一维输入变量，采用本文所提2 种算法以及2 种MCS 对照方法分别进行计算，结果如表1 所示，其中双层MCS 算法表示在每一个观测样本值处，都采用MCS 方法求解式（4）中的可靠性分析问题，得到相应的后验分布参数，进而通过历遍观测区间的方式得到后验分布参数区间。单层MCS 算法表示将观测变量看作观测区间中的均匀随机变量，由MCS 方法求解式（4）中的可靠性分析问题，即可得到满足条件的后验分布样本。本例中输入变量先验分布和似然函数满足共轭关系，因此可由式（24）在每一组观测样本处解析求得精确后验分布参数，用来对比验证本文算法对后验样本分布求解的可行性和准确性。

表1 输入变量X 后验分布参数Table 1 Posterior distribution parameters of input variables X

从表1 中数据可以看到，4 种方法所得到的后验分布参数均收敛至标准精确解析解，验证了本文所提算法框架的可行性和准确性。

图3 给出了各种方法计算得到的输入变量的后验分布及先验分布图。其中，精确解析解为观测值取均值（即不考虑观测不确定性）时由式（24）计算得到的标准解析解，PDF 为概率密度函数，从图3 中可以看出，4 种方法计算得到的后验分布概率密度曲线均收敛至标准解析解。与不考虑观测不确定性的精确解析解相比，当考虑观测不确定性时，贝叶斯更新后的输入变量后验分布不再是确定的单一函数而是一组区间分布函数，双层算法可以得到完整的后验分布概率密度曲线族，形成后验分布域，而单层算法可以得到平均后验分布曲线，并且与精确解析解吻合很好。另外，通过对比图3 中变量先验概率分布和后验概率分布可以发现，相比于先验概率分布，经过贝叶斯更新后变量的后验概率分布发生改变，主要变化体现在后验分布概率密度函数曲线更集中、分散性更小，这表明该线性系统输入变量分布参数的不确定性得到有效降低，证明了所提算法的有效性。

图3 数值模型输入变量先验及后验分布Fig.3 Prior and posterior distribution of numerical model input variables

4.2 悬臂梁结构

某矩形截面悬臂梁如图4 所示，其受到水平、竖直方向的载荷X、Y的作用，以其自由端位移不超过D0为约束建立功能函数为

图4 悬臂梁结构图Fig.4 Structure diagram of cantilever beam

式中：S1、S2为在准确后验分布参数下观测得到的位移，由位移观测数据及观测误差可得到S1∈[0.69，0.72]、S2∈[0.68，0.71]；σε1、σε2分别为2 次独立试验中位移观测误差的标准差，取σε1=σε2=0.03。本例考虑的先验分布参数如表2所示。

表2 矩形截面悬臂梁结构输入变量假定的后验分布参数及先验分布参数Table 2 Assumed posterior distribution parameters and prior distribution parameters of input variables for rectangular cross-section cantilever beam structure

表3 给出了观测样本为50 时该悬臂梁结构模型经过贝叶斯更新后输入变量的后验分布参数。结果表明4 种方法计算得到的后验分布参数与准确解均吻合得很好。图5 中进一步给出了在50 个观测样本下4 种方法计算得到的后验分布与准确后验分布的对比图，进一步证明了本文方法得到的完整后验分布与准确解也吻合得很好，其中双层算法可以得到完整的后验分布族，而单层算法可以得到后验分布的平均值，与不考虑观测不确定性的准确解更为接近。图5 同时给出了在观测区间内不同观测样本量下单层MCS 方法计算得到的后验分布与标准后验分布的对比。

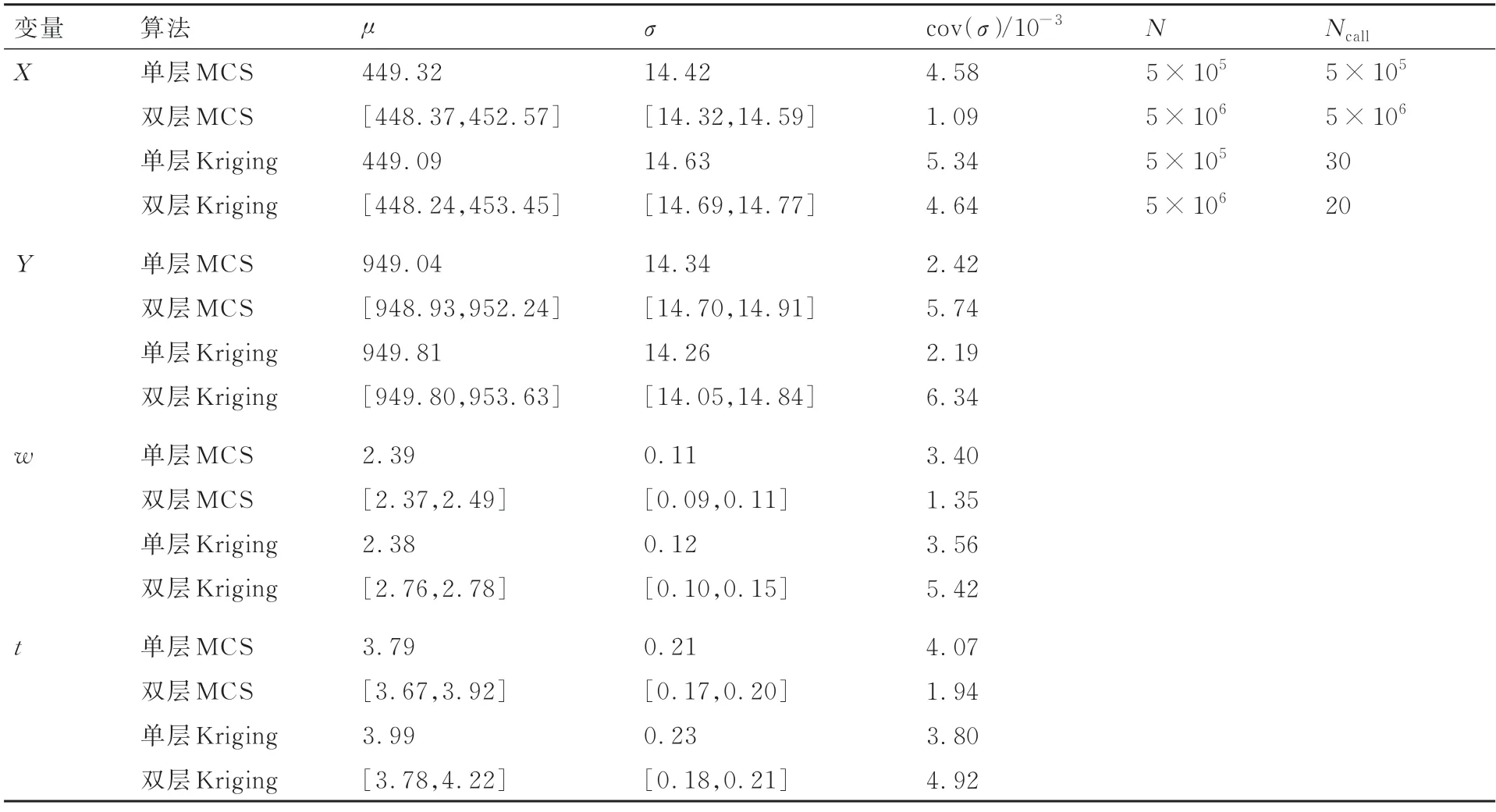
表3 矩形截面悬臂梁结构输入变量后验分布参数（50 个观测样本）Table 3 Posterior distribution parameters of input variables for rectangular cross-section cantilever beam structure（50 observed samples）

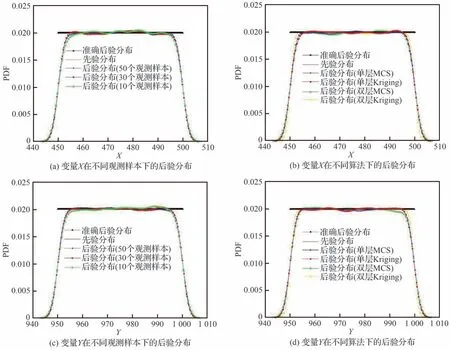
图5 悬臂梁结构输入变量先验及后验分布Fig.5 Prior and posterior distribution of input variables for cantilever beam structure

可以看出，对于变量X、Y，在不同观测样本量下，经过贝叶斯更新得到的后验分布参数与先验分布参数相比变化很小，这表明在先验分布极为准确的情况下，经过本文贝叶斯更新模型所得到的后验分布几乎不变，与准确的后验分布保持一致；对于先验分布很不准确且分散性很小的变量w，随着观测样本量的增加，经过本文贝叶斯更新模型所得到的后验分布逐渐收敛于准确分布，后验均值逐渐增大收敛于准确的后验均值，后验方差逐渐增大更接近于准确的后验方差；对于先验分布不准确且分散性较大的变量t，经过贝叶斯更新后的均值收敛于准确后验均值，后验分布概率密度函数曲线更为集中、分散性更小接近真实值。证明了本文贝叶斯更新模型对于提高观测不确定性下的模型准确性。

对于该显式功能函数算例，利用单层MCS方法，需要调用功能函数5×105次得到收敛的后验样本，而单层Kriging 方法由于使用了代理模型，仅需要调用30 次功能函数便可得到收敛的后验样本。双层MCS 方法由于需要在外层历遍观测区间，需要更大的计算量，调用功能函数5×106次，同样，双层Kriging 算法由于使用代理模型仅需要调用20 次功能函数。单层Kriging 算法由于直接建立起似然函数与观测变量和基本随机变量的代理模型，其变量维度比双层Kriging 算法更高，为保证模型精度，需要更多建模样本对来训练Kriging 模型，因此单层Kriging 算法调用原始功能函数次数比双层Kriging 算法要高，但单层Kriging 算法相比于双层Kriging 算法需要更小的样本池，对于功能函数计算时间可以忽略的显示功能函数，计算耗时一般会更短。

4.3 机翼结构

机翼结构是飞机的重要部件之一，安装在机身上，其最主要作用是产生升力，与尾翼一起形成良好的稳定性与操作性。另外可以在机翼内部装载弹药、设备和油箱，在机翼上可以安装起落架、发动机、悬挂导弹、副油箱及其他外挂设备。本节主要研究一个简化的机翼模型，该机翼模型主要由桁条、翼肋、翼墙、蒙皮组成。通过ANSYS 有限元分析软件对该简化的机翼模型进行静力学分析。在该有限元模型建模过程中，桁条采用杆单元结构，其中横截面积为A、弹性模量为E1。翼肋和翼墙采用板单元结构，其中弹性模量为E2、厚度为θ2。蒙皮也同样采用板单元结构，其中弹性模量为E1、厚度为θ1。以上单元材料泊松比均为0.3。该机翼几何外形及其所受外载荷如图6 所示，该机翼中由杆板结构形成的一个封闭盒段的长度为L。此外，由于机翼主要的受力形式为分布力和集中力，因此在本例中假设该机翼模型受到的所有外载荷最终都近似为集中力，且载荷大小为P，如图6（a）所示。假设以上输入随机变量均服从正态分布，且其分布参数如表4 所示。对于该机翼模型进行有限元分析，可建立如图6（b）所示的机翼有限元模型，ANSYS静力学分析得到该机翼在Y方向上的位移云图，如图6（c）所示。将Y方向上的位移阈值设置为U0=0.2 m，若该机翼模型在Y方向上的最大位移超过0.2 m，则可认为该机翼模型发生失效，反之，则认为该机翼模型安全。将有限元模型计算得到的Y方向的最大位移U(A，E1，E2，θ1，θ2，P，L)作为模型的输出，以Y方向最大位移不超过U0为约束建立功能函数为g(A，E1，E2，θ1，θ2，P，L)=0.2-|U(A，E1，E2，|θ1，θ2，P，L)，可以定义似然函数L=(A，E1，E2，)θ1，θ2，P，L|S为

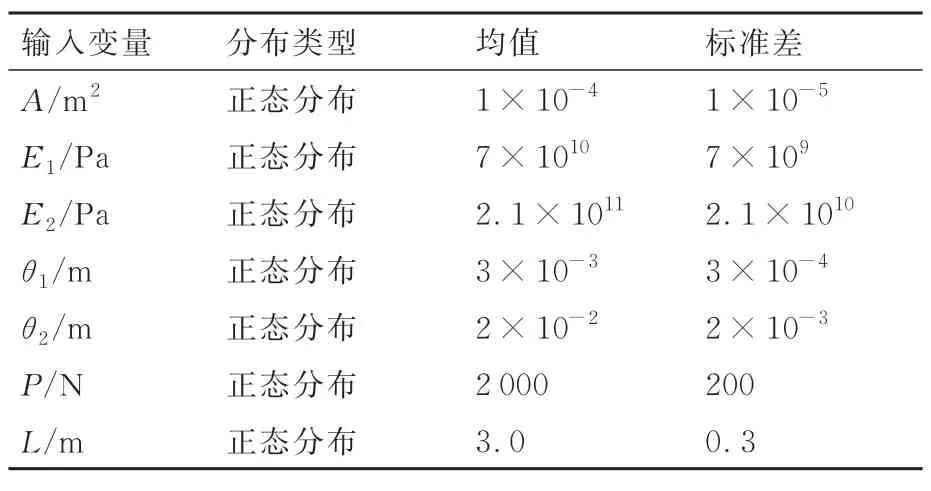
表4 飞机机翼有限元模型的输入变量先验分布参数Table 4 Prior distribution parameters of input variables for finite element model of aircraft wing

图6 机翼结构有限元模型图Fig.6 Finite element model diagram of wing structure

式中：S1为观测变量，由试验中对机翼Y方向最大位移观测得到，由机翼位移观测数据及其观测误差可得到S1∈[0.03，0.08]；σε1为位移观测误差的标准差，取σε1=0.01。

表5 给出了该机翼结构模型经过贝叶斯更新后输入变量的分布参数，从表中数据可以看到，利用单层MCS 方法，需要调用有限元模型3.2×104次才能得到收敛的后验样本，而单层Kriging方法，仅需要调用327 次功能函数便可得到收敛的后验样本。双层MCS 方法需要调用功能函数3.2×105次，而双层Kriging 算法仅需要调用268次有限元模型。2 种代理模型算法均大幅减少了有限元模型的调用次数，极大地缩短了计算耗时，提高了计算效率。

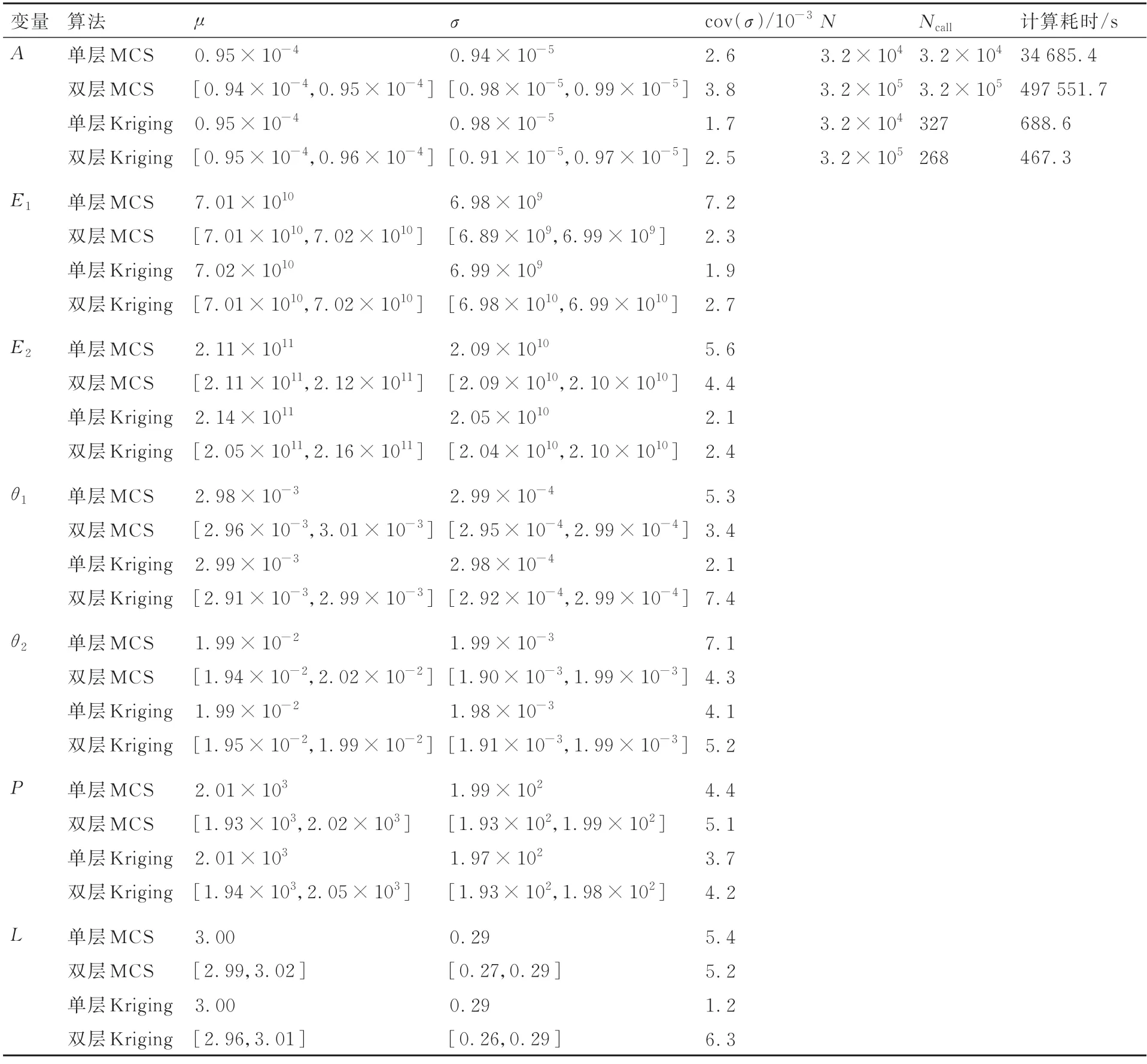
表5 飞机机翼结构输入变量后验分布参数Table 5 Posterior distribution parameters of input variables for aircraft wing structure

图7 给出了各种方法得到的机翼结构有限元模型输入变量的后验分布和先验分布图，从图7 中可以看出，4 种方法计算得到的后验样本分布基本一致，通过对比MCS 方法可以得到，本文所提的单层Kriging 及双层Kriging 算法均能够准确计算得到后验样本分布；通过对比图7 中各变量先验概率分布和后验概率分布可以发现，除了机翼截面积A，其他变量的后验概率分布相比于先验概率分布变化均不大，这表明这些变量的先验分布较为准确。截面积A的后验概率分布相比于先验概率分布变化较大，除了均值的移动外，后验分布概率密度函数曲线分散性也更小，这表明该机翼结构截面积A的先验分布不准确，经过贝叶斯更新后分布参数的不确定性得到降低。本例证明了所提方法应用在工程结构大型有限元模型贝叶斯更新过程中的高效性和准确性，具有一定的工程指导意义。

图7 飞机机翼结构输入变量先验及后验分布Fig.7 Prior and posterior distribution of input variables for aircraft wing structure

5 结论

针对已有贝叶斯更新方法无法考虑实际中存在的观测不确定性问题，建立了观测不确定性下的贝叶斯更新模型，并提出了模型求解的两种高效算法。3 个算例结果表明，所建贝叶斯更新模型通过将观测不确定性情况下的贝叶斯更新问题转化为区间和随机变量共同作用下的可靠性分析问题，能够充分考虑观测中实际存在的不确定性和基本变量的随机不确定性，对输入变量的先验分布参数进行有效的校正。所发展的2 类算法通过Kriging 模型能够在保证精度的同时大幅提高观测不确定性下贝叶斯模型更新的效率。双层Kriging 算法可以精确地得到后验分布参数的取值区间，单层Kriging 算法可以高效地给出后验分布参数的平均估计，并且2 种算法都能够给出输入变量准确完整的后验分布。所建更新模型及其求解的2 类算法实现了观测不确定性下贝叶斯模型更新的量化估计。需要说明的是，由于本文所提算法直接采用MCS 抽样使得样本池规模较大，影响了观测不确定性下贝叶斯模型更新的效率，可采用一些高效的抽样方法如重要抽样方法等进一步缩减样本池规模，提高算法的计算效率和稳健性。