张拉整体式伸展臂结构设计与刚度分析

2024-01-20张静郭凯郭宏伟刘荣强寇子明

航空学报 2023年24期

关键词：结构单元约束条件构型

张静，郭凯，郭宏伟，刘荣强，寇子明

1.燕山大学机械工程学院，秦皇岛 066004

2.河北省轻质结构装备设计与制备工艺技术创新中心，秦皇岛 066004

3.太原理工大学机械与运载工程学院，太原 030024

4.哈尔滨工业大学机电工程学院，哈尔滨 150006

张拉整体结构是一种由只受压力的离散杆构件与只受拉力的连续索构件构成的预应力自平衡铰接结构，属于小应变大位移的空间结构范畴。其以轻质灵活的索构件为主体，辅以局部刚性杆构件，仅需在构件中施加合适的预应力即可实现结构的刚化，不需要外部的支撑与荷载，具有刚度可调、形状可控、易于折展等显著优势［1-3］。

Yildiz 等［4］采用粒子群优化算法设计了轻量化、高刚度的二类三杆张拉整体式伸展臂。Kan 等［5］通过建立多节点集束索的方式得到一种10 个四棱台单元轴向连接的张拉整体式伸展臂，相比于经典索杆机构更易于展开。Zhang 等［6］以带端板的可变形张拉整体单元构造了多种一维张拉整体结构，拓展了伸展臂的应用场合。张拉整体式伸展臂的设计与分析多集中于找形方法选择、结构刚度比较与稳定性判定等方面。找形研究中，力密度法［7］是一种最常用、最基础的静力学找形方法。Lee 等［8］将力密度法与遗传算法相结合，提高了力密度法找形效率。Lu 等［9］考虑张拉整体结构的力学特性，使用动态松弛法去搜寻索中预应力，并完成找形研究。Pellegrino［10］运用非线性规划法，将张拉整体结构的找形问题转化为约束最小化问题，得到杆长最长的张拉整体结构。Kanno 等［11-13］将基结构法与混合整数线性规划法（MILP）相结合，以节点坐标位置为已知输入量，求得最终结构中各节点间的拓扑关系与各构件内力。Wang 等［14-15］在其研究基础上，进一步提出了混合整数二次规划法（MIQP）与混合整数半定规划法（MISDP）以解决张拉整体结构找形中各构件力的对称性与预应力缺失等问题。在伸展臂稳定性与刚度研究方面，Connelly［16-17］从数学角度提出了张拉整体框架的预应力稳定、超稳定等重要概念。Guest［18］研究发现张拉整体结构体系的切线刚度矩阵由线性刚度矩阵和几何刚度矩阵两部分组成。张沛［19］将确定形态的张拉整体结构划归到不同稳定等级当中，极大地便利了结构工程师设计的过程。罗阿妮［20］以三杆张拉整体结构单元的有限元模型为例，分析了不同因素对该经典结构单元刚度的影响程度。Cai 等［21］基于特征值分析法分别对经典三棱柱与星型张拉整体机构单元刚度矩阵特征值随构件中预应力水平变化的趋势进行了分析。

本文首先建立混合整数线性规划法所需的基本变量、约束条件与目标函数的数学模型，并由基结构法得到形状确定的张拉整体结构单元的节点坐标与所有可能构件。然后将各数学模型与所得基结构相结合，通过改变约束条件中控制参数拓扑找形得到多种结构单元构型，并基于改进型麦克斯韦尔准则和平衡矩阵奇异值分解法对所得单元构型以及现有经典单元构型完成稳定性判定及刚度比较，优选得到2 种单元构型。其次基于模块化设计思想提出两种构造伸展臂的方式，并分别得到2 种张拉整体式伸展臂。最后分别研究了不同预应力水平、约束方式、构件截面尺寸对两种伸展臂弯曲刚度的影响并明确了2 种伸展臂在各种情形下的刚度大小关系。

1 数学模型

建立混合整数线性规划数学模型中所需的基本变量、约束条件与目标函数，以便对基结构法所生成的基结构构件集合进行筛选与定义，即剔除构件集合中冗余构件，并指定剩余构件为索构件或杆构件，从而得到满足条件的张拉整体结构单元。

1.1 基本变量

三维空间中的n个节点的集合用V表示，任意节点两两连接可得到元素总数为b的构件集合E。节点总数n与所有可能构件的总数b之间的关系为

为了表征前述混合整数线性规划法对基结构构件集合的划分结果，构件集合E可划分为3 个两两不相交的子集S、C、N，且满足：

式中：S为杆构件集合；C为索构件集合；N为冗余构件集合。

首先，分别引入2 个0-1 整数变量xi∈{0，1}和yi∈{0，1}用作定义构件类型的基本变量，且与集合S、C、N之间的关系为

式中：i为集合E中第i个构件。

然后，同样引入0-1 变量nj∈{0，1}表示集合V中任意节点j是否存在于最终结构中，VΟ和VΙ分别表示剔除节点的集合与保留节点的集合，即有

最后，引入描述张拉整体结构中各构件内力的连续变量向量t=(ti)∈Rb。考虑张拉整体结构定义与实际应用，ti与集合S、C、N之间的关系为

1.2 约束条件

约束条件1张拉整体结构中，杆只受轴向压力，索只受轴向拉力，由式（3）与式（6）可得构件内力属性约束条件为

式中：M和ε为2 个特定的正数，且满足0 ＜ε≪M。

约束条件2由结构中节点坐标和各构件拓扑连接方式可得张拉整体结构单元的平衡矩阵A∈R3n×b，各节点所受外载荷向量为f∈R3n，因此，平衡约束方程为

由于所研究的是不考虑结构自重与外载的自平衡张拉整体结构单元，因此式（8）又可写为

约束条件3为提高三维空间找形所得结构单元的稳定性，应首先保证结构中各节点的稳定性，从实际角度出发，1 个节点应至少连接3 个构件，则约束条件为

式中：Ej为连接于节点j的所有可能构件集合，下同。

约束条件4由式（3）结合实际可知，同一构件不能同时为杆与索，即有(xi，yi)≠(1，1)，据此设置约束条件为

约束条件5由于任意节点j的存在性与连接于节点j的构件存在性密切相关，根据文献［22］可得nj、xi、yi（i∈Ej）之间的关系为

约束条件6张拉整体结构存在多种分类方式，按照连接于同一节点最大杆数为k分类，可分别称为Class-k（k=1，2，…）型张拉整体结构［23］，该约束条件表达式为

约束条件7现有张拉整体结构找形问题通常可归结为其余各构件长度不变的情形下，求解杆件长度最长的约束优化问题，由此提出约束条件为

约束条件8为提高找形结果的准确性，文献［15］根据张拉整体结构每个节点均连接有杆和索的基本特征，引入约束条件为

1.3 目标函数

为了避免张拉整体结构单元在展开过程中易出现的柔性构件缠绕问题，应在满足约束条件的前提下尽量减少使用索构件，即寻求一种最简张拉整体结构。最简张拉整体结构目标函数表达式为

2 结构单元找形与优选

2.1 基结构

Zawadzki 等［24］在对比轻型伸展臂时提到一种4 层节点的扩展型八面体张拉整体结构单元，该单元因存在较多的独立机构位移模态而稳定性较差，且受限于杆构件交叉的情况，不利于伸展臂结构的构造。因此本文在该结构单元同层节点相对位置不变的基础上，调整不同层节点间相对转角，即第4 层节点（N5、N7）水平面坐标与第3 层节点（N6、N8）水平面坐标分别相对第1 层（N1、N3）与第2 层（N2、N4）逆时针旋转45°，得到如图1 所示的包含n=8 个节点和b=28 个构件的新的基结构。图中细线表示结构单元找形前的所有构件。

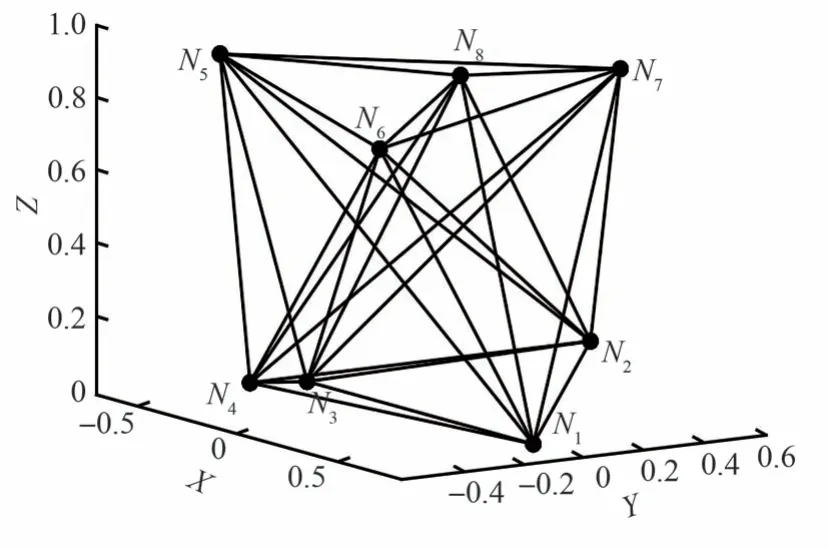
图1 基结构Fig.1 Ground structure

2.2 结构单元拓扑找形

基于上述基结构和式（7）～式（16）所给的约束条件和目标函数，设基结构中各节点均被采用，且M=100，ε=0.01，k=1，在MATLAB 中通过改变约束条件中的控制参数拓扑得到以下6 种张拉整体结构单元构型（图中红色粗线表示杆件，蓝色细线表示索件，黑色圆点表示基结构中的各节点）：

1）不限杆长，每个节点至少连接3 个构件，可得构型1，如图2 所示。

2）不限杆长，每个节点至少连接4 个构件，可得构型2，如图3 所示。

图3 单元构型2Fig.3 Element configuration 2

3）不限杆长，每个节点至少连接5 个构件，可得构型3，如图4 所示。

图4 单元构型3Fig.4 Element configuration 3

4）llimit=1，每个节点至少连接3 个构件，可得构型4，如图5 所示。

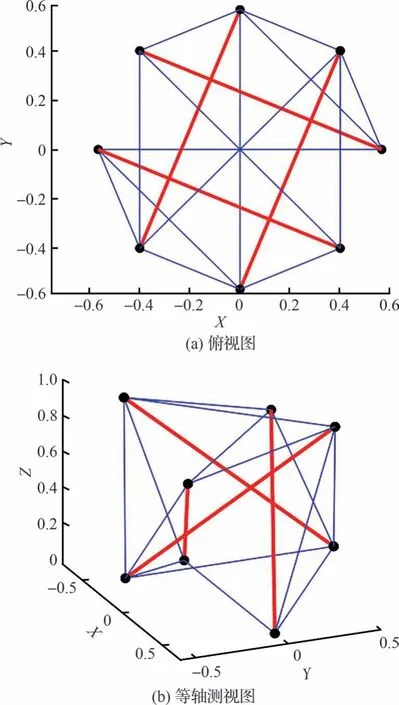
图5 单元构型4Fig.5 Element configuration 4

5）llimit=1，每个节点至少连接5 个构件，可得构型5，如图6 所示。

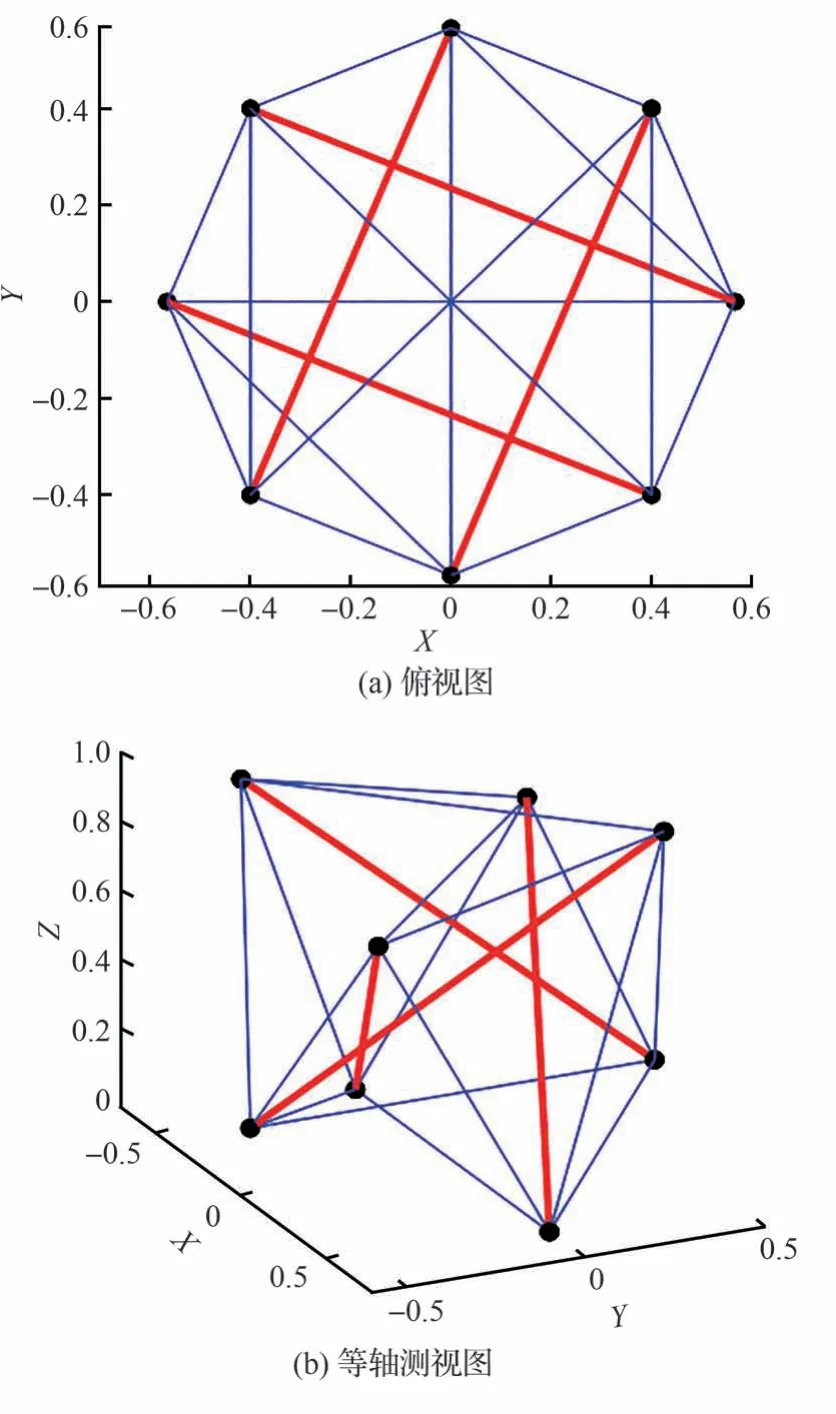
图6 单元构型5Fig.6 Element configuration 5

6）与构型3 条件相同，但是基结构节点旋向相反，得到与构型3 旋向相反的构型6，如图7所示。

图7 单元构型6Fig.7 Element configuration 6

以上拓扑所得张拉整体结构单元均包含4 根不连续的杆，满足Class-1 型张拉整体结构中节点数是杆数2 倍的条件。各单元构型的统计信息见表1。

表1 各单元构型统计信息Table 1 Element configuration statistics

由表1 可知，单元构型1、2、4 虽然满足所有约束条件，但由空间铰接结构的麦克斯韦尔准则［25］可知，这3 类单元构型不符合张拉整体结构ns＞0 且nm≥0 的定义，因此不做考虑。单元构型3、5、6 均满足ns＞0 且nm=0，属于第3 类空间铰接结构体系［26］，即静不定动定张拉整体结构。

2.3 稳定性判定与刚度比较

在衡量张拉整体结构的稳定性与刚度时，常引入结构的切线刚度矩阵K，其由线弹性刚度矩阵KE和几何刚度矩阵KG两部分组成，即有

式中：KE取决于结构的几何形状与构件刚度，而KG则与构件中的预应力水平密切相关。

通过MATLAB 编程进行数值计算可知单元构型3、5、6 均满足文献［27］中动定结构体系稳定性条件：

因此，这3 个单元构型均达到基本的稳定设计要求。其中，单元构型3 与单元构型6 仅旋向相反，其余相关参数类似。

现以相同的包络圆半径、高度、构件刚度及预应力水平分别构造单元构型3 与单元构型5、经典三棱柱/四棱柱、带附加索的三棱柱/四棱柱等6 类张拉整体结构单元并顺次编号。通过平衡矩阵奇异值分解法求解得到6 种单元构型的自应力模态与内部机构位移模态，并计算各单元构型切线刚度矩阵K的最小特征值以比较它们的刚度，所得各数据见表2。

表2 各单元构型稳定性与刚度参数信息Table 2 Configuration stability and stiffness parameter information of each element

由表2 可知，单元1（单元构型3）、单元2（单元构型5）和单元5（带附加索的三棱柱）均为静不定动定结构，同属于文献［27］中提到的稳定等级1，即单元构型稳定性最强且刚度大，该稳定等级中单元5 刚度最大，单元1 次之，单元2 最小。其余3 个单元则属于稳定等级2，即结构单元稳定但刚度较小，这3 个单元的刚度由大到小依次为单元3（经典三棱柱）、单元6（带附加索的四棱柱）、单元4（经典四棱柱），此计算结果和相关结论与文献［28-29］实验结果相同。

综上所述，拓扑找形所得单元构型3 稳定性与刚度仅次于带附加索的三棱柱张拉整体结构单元，且单元构型3 与经典（或带附加索）四棱柱张拉整体结构单元同为四杆张拉整体结构，前者在稳定性与刚度优于后者的情况下，索的数量也更少，完美契合目标函数。经验证，单元构型6 与单元构型3 有相同的性能，仅单元旋向不同，因此选择这2 种单元构造伸展臂。

3 伸展臂构造及可展分析

基于上述优选单元构型与模块化设计思想，提出2 种单元构型轴向拓扑方式，并分别构造2 种10 个单元的伸展臂。所得2 种伸展臂均为Class-2 型张拉整体结构，即伸展臂中杆构件之间通过节点直接相连。关于Class-2 型伸展臂的折展研究，引入集束索（Clustered）概念，将2 种伸展臂的边索均串联成连续滑动绳索单元，构成集束索。集束索的一端固定连接在伸展臂顶部节点，绳索连续滑动穿过伸展臂中多个节点后，另一端由底部节点引出连接至驱动器。通过驱动器的收紧与释放，改变伸展臂中集束索的有效长度驱动控制伸展臂的折叠与展开。同时伸展臂中所有层索均由弹簧替代，当驱动器收紧集束索而使伸展臂折叠时，各弹簧均被拉伸以储存势能，随着驱动器释放集束索，弹簧弹性势能被释放，从而实现伸展臂展开。

以2 个单元的张拉整体结构的构造方式与折展驱动方式为例，进行2 种伸展臂的构造说明和可展分析。文中以下示意图中红色圆柱体为杆构件，蓝色圆柱体为由弹簧代替的层索构件，绿色圆柱体为集束索构件。

3.1 相同单元构造及可展分析

将10 个相同的单元构型3 沿轴向叠加，各单元之间序号相同的节点相连，各单元序号相同节点之间的索构件相互重叠，因此重叠部分只保留一组索构件。叠加效果如图8 所示。

图8 相同单元构造方式Fig.8 Same element construction

将图8 中边索N11-N6、N6-N1串联构成集束索N11-N6-N1，集束索一端固定在节点N11，绳索连续滑动穿过节点N6和N1，集束索另一端由节点N1引出，继续延伸连接至驱动器。以同样方式继续构成了集束索N12-N7-N2、N9-N8-N3、N10-N5-N4，共连接4 个驱动器。所有层索均由弹簧替代，底部4 节点N1-N4通过球铰连接在基座上。依据前述折展驱动原理，相同单元构造方式下的两单元张拉整体结构的折展示意图如图9 所示。

图9 相同单元构造折展过程Fig.9 Folding process of the same element construction

以上述构造方式与折展驱动方式得到的10 个单元的伸展臂命名为SS 伸展臂，如图10 所示。

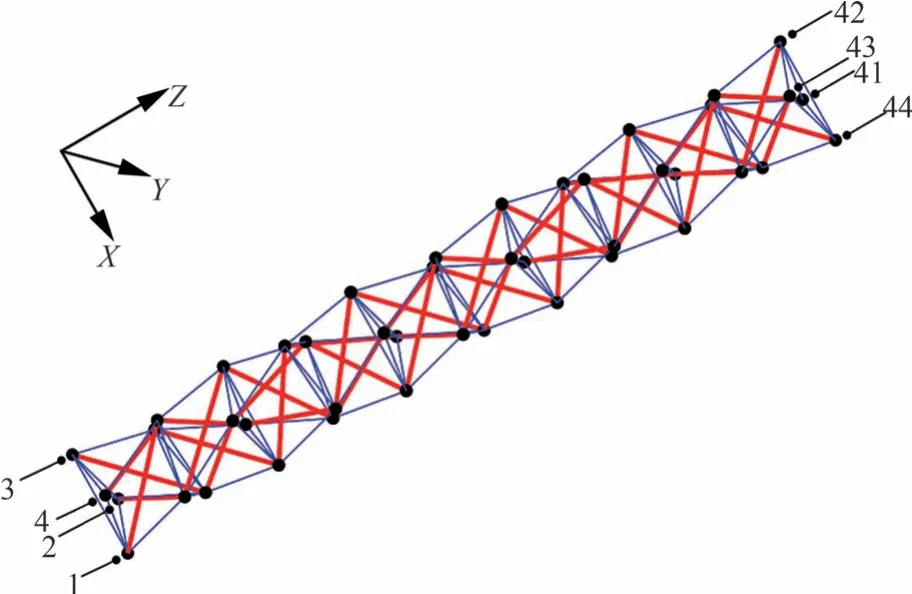
图10 SS 伸展臂Fig.10 SS deployable mast

3.2 两类单元交替构造及可展分析

将单元构型3 和单元构型6 沿轴向由下至上交替排列，奇数层为单元构型3，偶数层为单元构型6。其中，单元构型3 的节点N5、N6、N7、N8分别与单元构型6 的节点S4、S1、S2、S3一一对应连接，各相同节点之间索构件重合，连接处重叠部分同样只保留一组索构件，叠加效果如图11 所示。

图11 2 类单元交替构造方式Fig.11 Alternate construction of two types of elements

由前述折展原理与驱动方式，分别构成了N9-N6-N1、N10-N7-N2、N11-N8-N3、N12-N5-N44 根集束索，4 根集束索一端分别固定连接在节点N9、N10、N11、N12，另一端分别由节点N1、N2、N3、N4引出延长，连接至4 个驱动器。所有层索同样均由弹簧替代，底部4 节点N1-N4通过球铰连接在基座上。该构造方式下的折展示意图如图12 所示。

图12 2 类单元交替构造折展过程Fig.12 Folding process of alternate construction for two types of elements

以上述构造方式与折展驱动方式得到的10 个单元伸展臂命名为SN 伸展臂，如图13所示。

图13 SN 伸展臂Fig.13 SN deployable mast

4 伸展臂刚度仿真分析

依据图10 和图13 中所示节点排布位置及构件连接关系，本文在有限元分析软件ANSYS APDL 中通过编程建立了含40 个杆单元与106 个索单元的张拉整体式SS 伸展臂与SN 伸展臂有限元模型并进行分析。2 种伸展臂结构同类构件初始预应力水平均相同，都采用外径60 mm，壁厚4 mm 的Q345 钢管为杆构件以及公称直径为8.6 mm 的高强钢绞线为索构件。其中，索构件的预紧长度极限为其原长的0.681%，详细结构参数信息见表3。

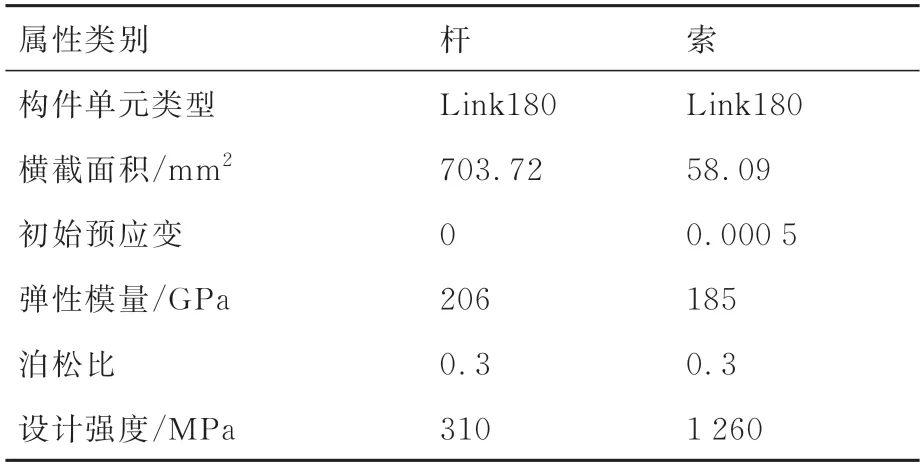
表3 构件与材料属性信息Table 3 Element and material property information

本文所设计的2 种张拉整体式伸展臂均等效为一端固定，一端承受集中力作用的悬臂梁模型。对2 种伸展臂顶部均施加沿着X轴负方向的逐渐增加的外载荷F，并平均分配到顶部4 个节点（节点41～节点44），各节点所受外载荷均为F/4，使得伸展臂发生弯曲变形。鉴于张拉整体结构本身较强的几何非线性特性，求解前需打开大位移分析开关。以变形后的伸展臂结构顶部4 个节点沿X轴负方向位移大小的平均值为该伸展臂的最大挠度wB，在伸展臂长度L已知的情况下，伸展臂在不同工况下的弯曲刚度为

式中：EI 为伸展臂的弯曲刚度，单位为N·m2。

在上述条件下研究不同索构件预应力水平及不同约束方式对伸展臂弯曲刚度的影响，并在给定外载荷与索构件预应力的情况下研究成倍增长的构件横截面积对2 种伸展臂刚度质量比的影响。

4.1 不同预应力水平下伸展臂刚度分析

无多余约束方式（即分别约束节点1 的3 个自由度，节点2 在Y、Z方向的自由度，节点3 与节点4 在Z方向的自由度）下，分析讨论当索构件预紧长度分别为其原长的0.05%、0.10%、0.15%、0.20%、0.25%以及0.50%这6 种不同预应力水平下，2 种伸展臂弯曲刚度随着外载荷的变化的规律，2 种伸展臂载荷-位移曲线和载荷-刚度曲线如图14～图17 所示。

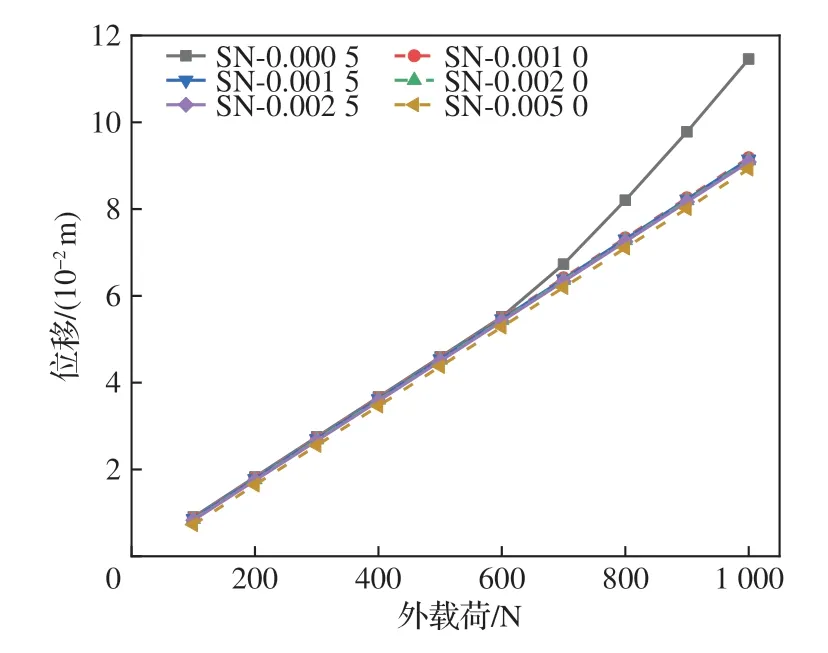
图14 SN 伸展臂载荷-位移变化曲线Fig.14 Load-displacement curves of SN deployable mast

由图15 和图17 可知，在任意相同外载荷作用下，张拉整体式SS 伸展臂和SN 伸展臂的弯曲刚度均随着索构件预应变的增加而增加，2 种伸展臂沿X轴负方向的变形也均相应地减小。但是当2 种伸展臂索构件预紧长度分别为其初始值的2 倍及以上，且SN 伸展臂与SS 伸展臂分别承受400 N 和300 N 及以上外载荷时，伸展臂在承受相同外载荷作用下索构件预应变的增加对伸展臂弯曲刚度的影响逐渐减小，伸展臂弯曲变形敏感度下降。这是由于随着结构构件中预应变增加，张拉整体式伸展臂刚化效果明显增强，近似为一刚性结构，此时伸展臂的刚度随外载荷的变化不再明显。

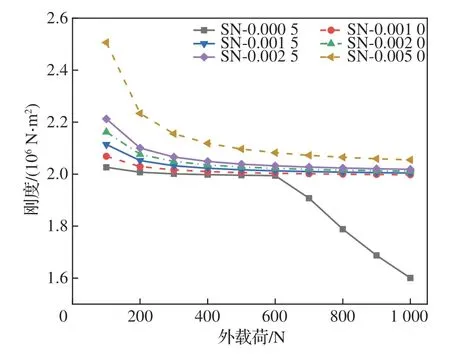
图15 SN 伸展臂弯曲刚度变化曲线Fig.15 Bending stiffness curves of SN deployable mast

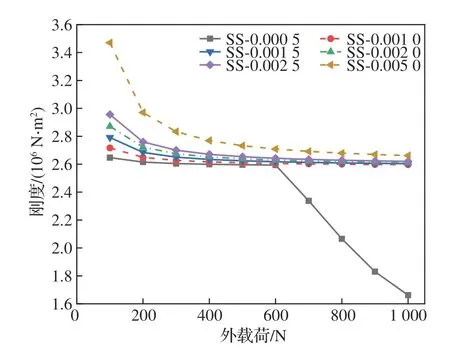
图17 SS 伸展臂弯曲刚度变化曲线Fig.17 Bending stiffness curves of SS deployable mast

同时对比了相同预应变水平下，外载荷的增加对2 种伸展臂刚度的影响。可以清楚地看到，在初始预应变不变的情况下，当外载荷小于600 N时，2 种伸展臂弯曲刚度受外载荷变化影响较小，而在600 N 以上时，随着外载荷的增加2 种伸展臂弯曲变形大幅增加。出现该明显下降趋势的原因为伸展臂在该工况下存在构件内力小于结构所受外载荷的索构件，SN 伸展臂在初始预应变情况下，当其所受外载荷为600 N 时，此时结构中索构件内力最小值为1 000.02 N，大于所受外载荷；而当其所受外载荷为700 N 时，结构中索构件内力最小值为341.91 N，小于所受外载荷，经验证SS 伸展臂也存在同样构件内力与外载荷大小关系。当2 种伸展臂中索构件预应变水平分别为其初始值的2 倍及以上时，随着外载荷的增加，弯曲刚度均呈现逐渐减小的趋势，且变化量也逐渐减小，符合张拉整体结构非线性变化特征。验证了张拉整体式结构具有良好的自适应性，在受到外载荷后自动调整构件内力分布与节点位置，以提高结构自身对外界载荷变化的适应能力，维持自身的功能特性。

对比图15 和图17，2 种伸展臂分别在承受1 kN 外载荷时，SN 伸展臂杆构件最大等效应力为133.89 MPa，索构件为1 243.9 MPa，而SS 伸展臂杆构件最大等效应力为133.87 MPa，索构件为1 244.5 MPa，均未超过结构设计强度。该载荷工况下，2 种伸展臂随索构件预应变水平变化的弯曲刚度数值见表4。

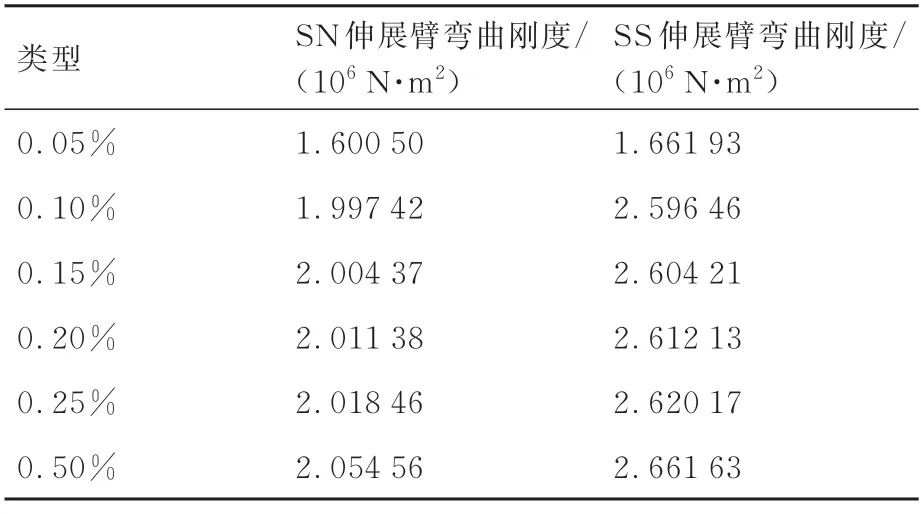
表4 非全约束下弯曲刚度数值变化Table 4 Numerical variation of bending stiffness under incomplete constraint

由表4 可知，当2 种伸展臂均承受相同最大弯曲外载荷时，在索构件的抗拉强度、杆构件的屈服强度范围内，无论索构件预应变水平如何变化，SS 伸展臂弯曲刚度总是大于SN 伸展臂，经验证其余载荷工况下也存在相同的规律。因此在承受合理弯曲载荷的工况下，为减少伸展臂的变形，宜采用SS 伸展臂。

4.2 不同约束方式下伸展臂刚度分析

本节将伸展臂底部4 节点的非多余约束方式转换为全约束方式（即节点1～节点4 的3 个方向的自由度均被约束）以研究2 种张拉整体式伸展臂在索构件预应力水平变化的情况下结构刚度随外载荷的变化趋势。全约束方式下2 种伸展臂载荷-位移曲线和载荷-刚度曲线如图18～图21 所示。

图18 SN 伸展臂载荷-位移变化曲线Fig.18 Load-displacement curves of SN deployable mast

分析图19 和图21 可知，在相同外载荷作用下2 种伸展臂弯曲刚度值均随索构件预应变的提高而增加，但是在索构件预应变值为其初始值的2 倍及以上时增加幅度较小。同样，分析了在相同预应变的情况下，外载荷的增加对2 种伸展臂刚度的影响。当预应变为初始值的2 倍及以上时，外载荷在合理范围内变化对伸展臂弯曲刚度无影响。而索构件在初始预应变时，2 种伸展臂弯曲刚度均随着外载荷的增加先保持恒定而后下降，且当SN 伸展臂所受外载荷为500 N 和SS伸展臂所受外载荷为400 N 以上时，由于部分索构件内力小于该工况下的外载荷出现伸展臂弯曲刚度大幅下降的趋势。这一变化趋势与非多余约束方式下的情况相似。

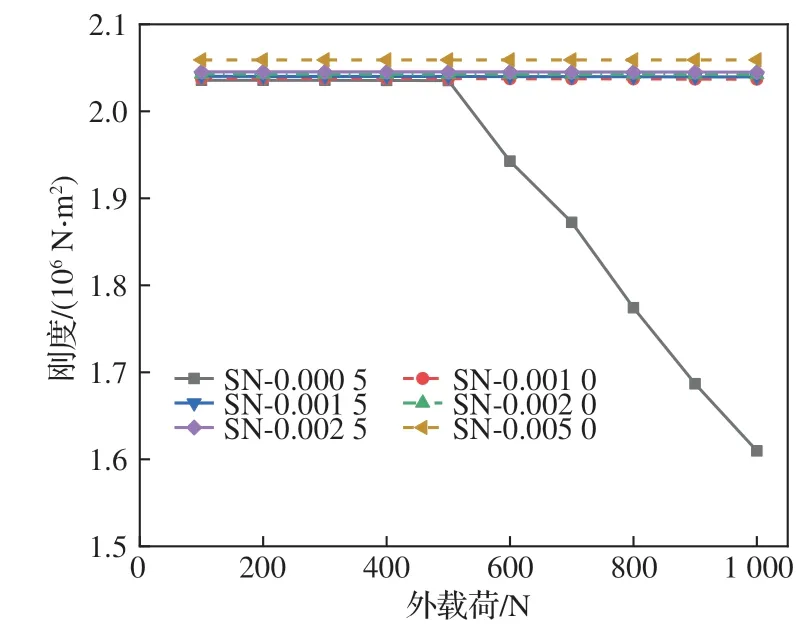
图19 SN 伸展臂弯曲刚度变化曲线Fig.19 Bending stiffness curves of SN deployable mast

图20 SS 伸展臂载荷-位移变化曲线Fig.20 Load-displacement curves of SS deployable mast

图21 SS 伸展臂弯曲刚度变化曲线Fig.21 Bending stiffness curves of SS deployable mast

对比图19 和图21，2 种伸展臂分别承受1 kN外载荷时，SN 伸展臂杆构件最大等效应力为132.63 MPa，索构件为1 111.9 MPa，而SS 伸展臂杆构件最大等效应力为133.81 MPa，索构件为1 112.6 MPa，均在构件设计强度许用范围之内。该载荷工况下，2 种伸展臂弯曲刚度随索构件预应变大小变化的情况见表5。

表5 全约束下弯曲刚度数值变化Table 5 Numerical variation of bending stiffnes under full constraint

由表5 可知，同样是在最大弯曲外载荷作用下，2 种伸展臂之间刚度大小关系与非多余约束方式类似，所得结论相同。

分别对比图15 和图19、图17 和图21、表4 和表5 可知，对于SN 伸展臂，在索杆构件的应力临界值范围内，在索构件预应变水平越高，所受外载荷越大的情况下，非多余约束方式下伸展臂弯曲刚度大于全约束方式时的刚度，反之，则全约束方式下弯曲刚度较大；对于SS 伸展臂，不同约束方式的刚度大小关系与SN 伸展臂相同。同时，全约束方式会削弱索构件预应变变化以及水平外载荷变化对2 种伸展臂弯曲刚度的影响。