基于GA-BP神经网络的汽车润滑系统中磨粒分类的研究

2024-01-19王飞何磊张恩亮方宇

长春工程学院学报（自然科学版） 2023年4期

王飞,何磊,张恩亮,方宇

(1.安徽职业技术学院汽车工程学院,合肥 230011; 2.安徽农业大学经济技术学院,合肥 230036 )

0 引言

在汽车润滑系统中,磨粒通常是由于金属机件的磨损和颗粒物质的存在产生的[1]。通过分析磨粒可以了解汽车润滑系统的运行状态是否会出现故障,以及可能出现的故障类型[2]。由于磨粒的几何特点与表征受磨粒产生原因的影响,因此深入研究磨粒的形态特点与表征[3],可以对磨粒进行准确分类。

在早期的研究中,关于磨粒的辨认主要由铁谱研究领域的专家进行,由于人工分析图像耗时耗力,并且分析结果存在差异性,因此,对于铁谱图像的研究倾向于采用自动化识别的方法[3]。BP(Error Back Propagation Training)[4]也被叫作误差反向传播算法,BP神经网络可以对一些复杂模型进行分类,并将特定的参数赋予网络,可对网络训练后的参数初始化,是一种更新迭代训练网络的方法。遗传算法(Genetic Algorithm GA)[5]是仿效《物种起源》中优胜劣汰的理论而设计的一种机器计算模型样式。“遗传”二字,来源于生物在繁殖过程中每一代都会通过上一代传递和继承一部分基因及特征。在GA-BP神经网络遗传算法中,“遗传”主要表现在算法对神经网络权值和结构的搜索和优化过程上。通过模拟生物的遗传和进化过程,算法可以在较大的解空间中全局搜索,同时也可以根据问题的特性自适应地调整搜索策略,从而找到最优的网络权值和结构。GA-BP神经网络综合了遗传算法和BP神经网络算法的各项优势,能够通过优化学习率、权重和阈值等参数,提高网络的分类精度[6]。因此,本文采用基于GA-BP神经网络的自动识别方法,针对汽车润滑系统中磨粒的分类问题进行了深入研究。

本文通过对比不同磨粒的特征,将磨粒的外形特征作为函数的输入,由GA-BP神经网络的反馈调节来逐步减少误差值,使得输出在一定阈值,通过3次映射关系训练GA-BP神经网络,从而得到一个能准确识别磨粒种类且对硬件要求较低的神经网络,GA-BP神经网络能够满足汽车润滑系统中磨粒分类检测的准确性和高效性的需求。

1 BP神经网络模型

1.1 构建BP神经网络

BP神经网络算法计算网络误差平方最小值应用的是梯度下降法,其中的目标函数为网络误差平方。在BP神经网络中,通过复杂的非线性关系和简单的训练学习可以有效地把识别出的5组典型粒子分为:摩擦、切割、球形、疲劳和严重滑动。

BP神经网络包含输入层神经元个数、隐藏层神经元个数和输出层神经元个数,通过神经元计算权值连接。BP神经网络通过标记样本训练网络,使得输出值和期望值间的差值在设定的可控的范围内。当隐藏层神经元的个数h满足h=0.5(m+n)+a(a=1,2,3,…,10)时,其中输入层神经元的个数和输出层神经元的个数依次为m、n,由柯尔莫戈洛夫定理可知,3层神经网络可以准确地实现任何连续映射,达到训练网络识别汽车润滑系统中磨粒种类的目的。

BP神经网络模型如图1所示,可知将图像数据输入至输入层,通过输入层与隐藏层间的神经元计算权值,再把权值作为输入传递至隐藏层,经过隐藏层和输出层间的神经元最终计算出图像数据的输出阈值。

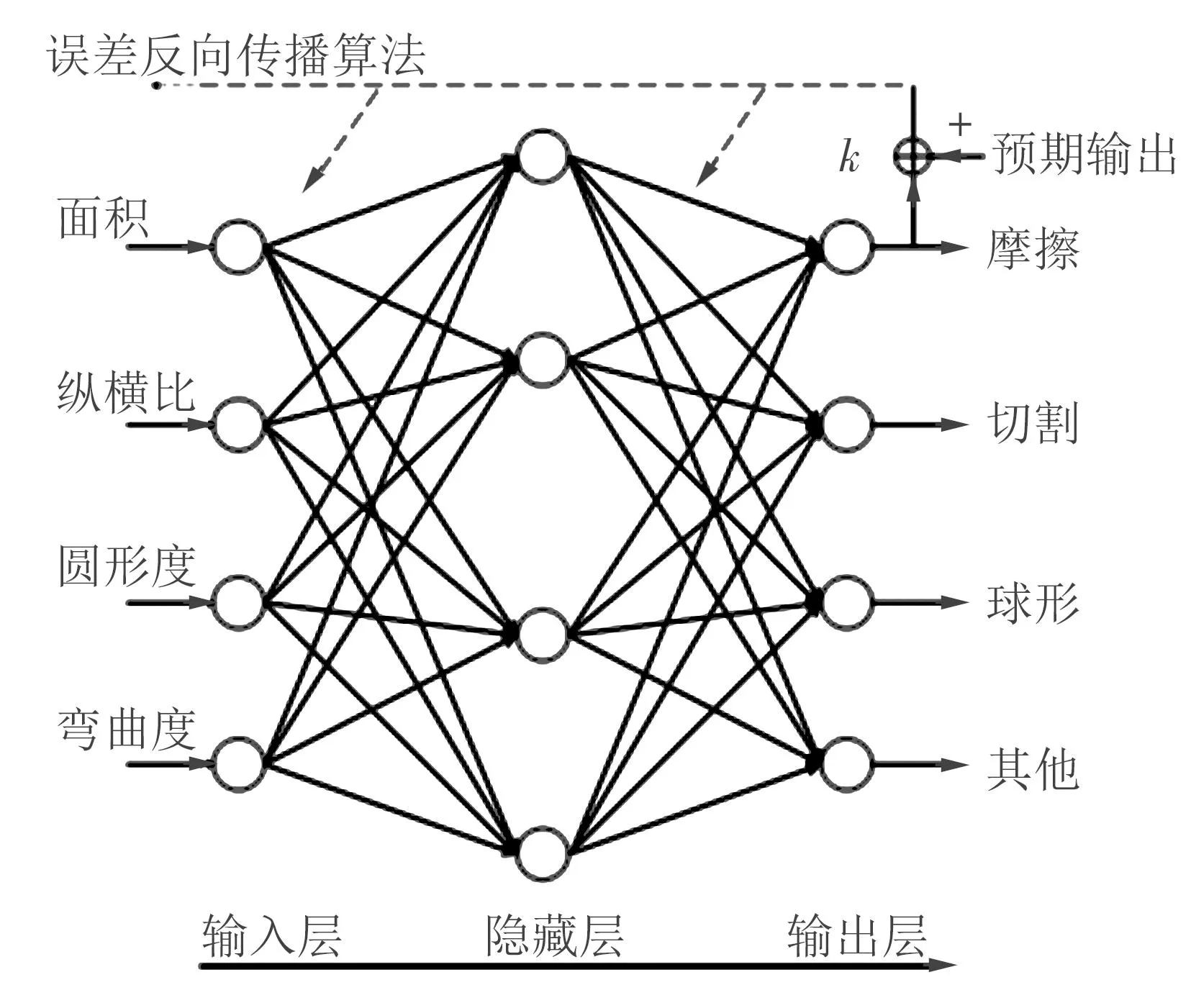
图1 BP神经网络模型

具备强大的学习能力是神经网络最大的特点,通过网络学习可逐步实现降低输出值和期望值的误差。BP神经网络是非线性的系统,通过输入层信息与输出层信息的映射关系将结果输出,而权值以及阈值间的持续更正是网络学习的实质,因此将调整后的权值及阈值再次输入至输入层,网络训练后会对权值及阈值做出调整,降低试验误差。

1.2 BP神经网络算法

通过适当设置隐藏层神经元的数量,可以建立从输入(磨粒参数)到输出(磨粒类型)的非线性映射关系。具体程序描述为

1)在初始化过程中将权重值和阈值用随机值连接。

2)通过被选择的输入(磨粒参数)及输出模式中某参数,计算隐藏层及输出层中各个单元的输出。

3)用公式(1)～(4)计算新的连接权重和阈值:

θk(t+1)=θk(t)+ηtσk,(t=1,2,…,p;k=1,2,…,l),

(1)

βj(t+1)=βj(t)+ηtσj,(t=1,2,…,p;j=1,2,…,m),

(2)

式中ηt为第t次训练迭代,σk为输出层第k个节点的误差,θk为输出层第k个神经元的阈值,σj为隐藏层第k个节点的误差,βj为隐藏层第k个神经元的阈值。

ωjk(t+1)=ωjk(t)+Δωjk(t),(t=1,2,…,p),

(3)

vij(t+1)=vij(t)+Δvij(t),(t=1,2,…,p),

(4)

式中t为训练迭代次数,ωjk为从隐藏层到输出层的权值,vij为从输入层到隐藏层的权值。

将式(4)权值初始化,重新执行第2步,再次训练神经网络,直到网络的输出均方误差(MMSE)达到一定范围或者迭代到一定次数,见式(5):

(5)

式中Ai为样本经过隐藏层处理后的实际输出,Ti为期望输出,N为样本数量。MMSE作为调整连接各层权值、阈值的关键因素,反复对网络初始化训练,直到MMSE收敛。

总之BP神经网络通过正向传播和反向传播学习,完成算法数据学习和特征选取工作,由此建立自己的学习规则。BP神经网络能够训练学习大量的样本,泛化能力极强,对于学习过的网络,其不仅可以对当前数据样本进行预测分析,还可以对新的数据样本作出预测判断。对于待学习的样本需要自行标注并一一对应。

在设置网络参数时,需要设置网络的学习率,若设置的学习率过大,网络可能会出现不收敛或者大幅振动的现象;若设置的学习率过小,网络的学习时间将大幅增加。同时网络设置的权值、阈值不会被网络记录,如果有新的样本输入,会导致之前学习的权值、阈值重置,影响网络学习效率。本文采用自适应学习率算法,因权值变化影响学习率变化,所以可增快模型的收敛速度,进而提高模型效率。BP神经网络分类模型是采取梯度下降法架构的,BP神经网络E-W曲线如图2所示。

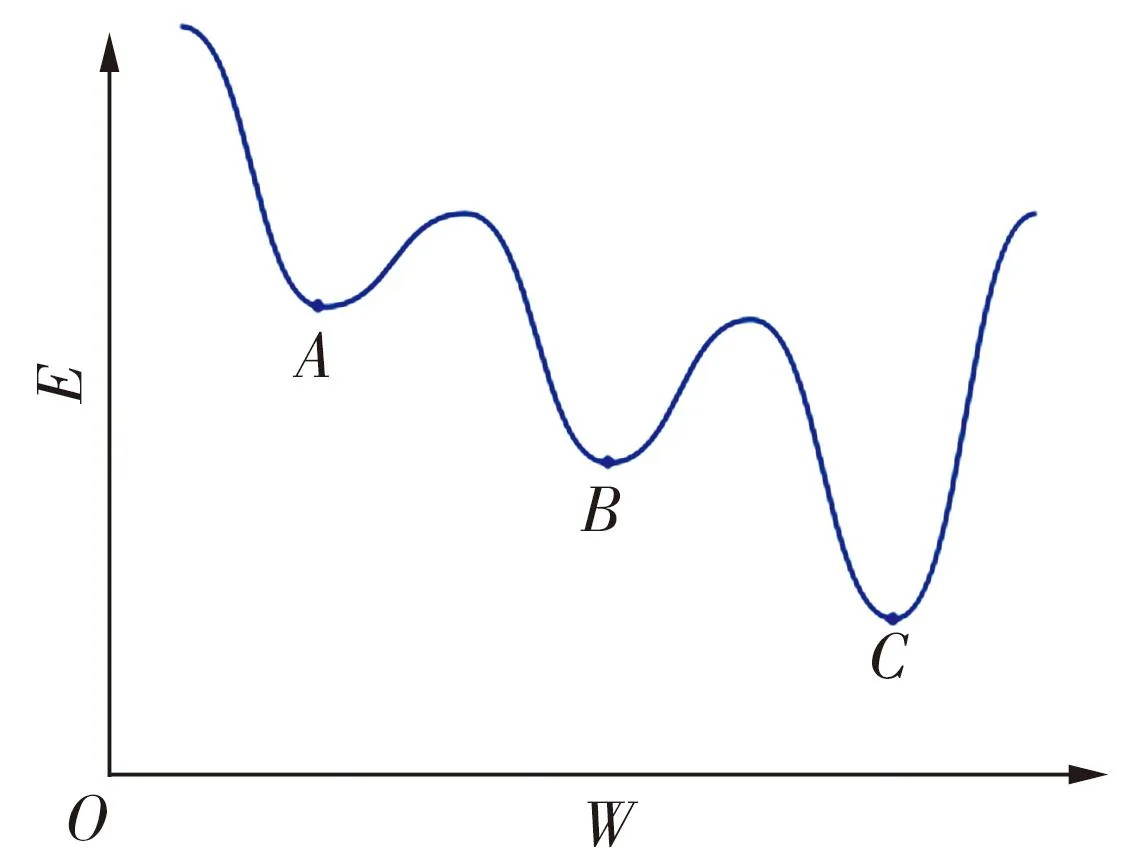
图2 BP算法E-W曲线

图2中W为梯度,E为评估误差,E-W曲线也被称为误差曲线,当图像斜率较小时,误差随权值变化不明显,表现为网络收敛速度慢或者不收敛,同时图中存在多个极小值点(A,B,C),会出现网络局部极小值,从而限制它,使它无法获取全局最优。

2 改进的BP神经网络算法

2.1 改进的GA-BP神经网络算法流程

遗传算法对BP神经网络的改进主要包含3部分:明确网络拓扑结构、优化阈值及权值、执行遗传操作。改进的GA-BP神经网络流程图如图3所示。

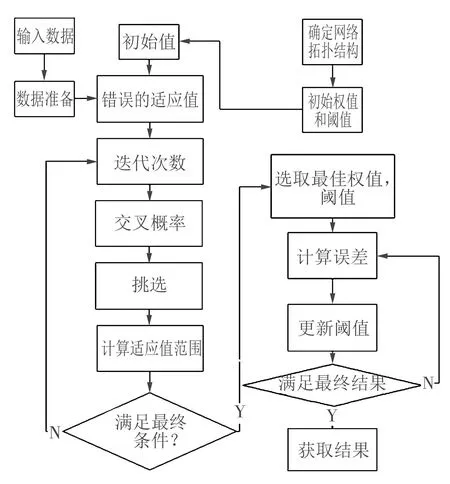
图3 改进的GA-BP神经网络流程图

2.2 优化拓扑结构和权值阈值

首先通过Newff()函数对网络进行BP神经网络构架,将输入层数据、隐藏层数据以及输出层数据进行归一化处理,把经过处理的数据作为参数传递给Sigmoid函数,并将该函数的输出结果映射到一个特定的区间范围内。由于Sigmoid函数值域为0～1,因此可以将Sigmoid函数作为输出函数,“0”为“神经元抑制”,“1”为“神经元兴奋”。把Newff()函数训练神经网络时所需要的输入作为测试集,再把测试集数据当成输入对网络进行测试,从而确定网络的可行性。测试集的输入、输出参数需要在网络初始化后进行随机排列,最后做归一化处理。

BP神经网络的阈值和权值决定着网络最终的误差,为了减少误差,增加网络的精确度,使用遗传算法对阈值和权值进行优化。遗传算法中使用适应度函数衡量个体的适应程度,高适应度的个体遗传可能性更高,低适应度的个体遗传可能性更低。本文所选用的适应度值是均方误差(MMSE)的倒数。编码构建从输入层到隐藏层的连接权值、从隐藏层到输出层的连接权值、a2+b2=c2隐藏层阈值以及输出层阈值。其构建的编码作为函数的输入,再将网络的期望值与测试值做差取倒数作为函数的输出。其计算公式为

(6)

式中f(i)为第i个神经元的适应度值,MMSEi为第i个个体实际输出(Ai)与期望输出(Ti)的均方误差。经历14个epoch迭代后,BP神经网络的适应度曲线走向缓和。BP神经网络和GA-BP神经网络算法分类的适应度值曲线如图4所示。

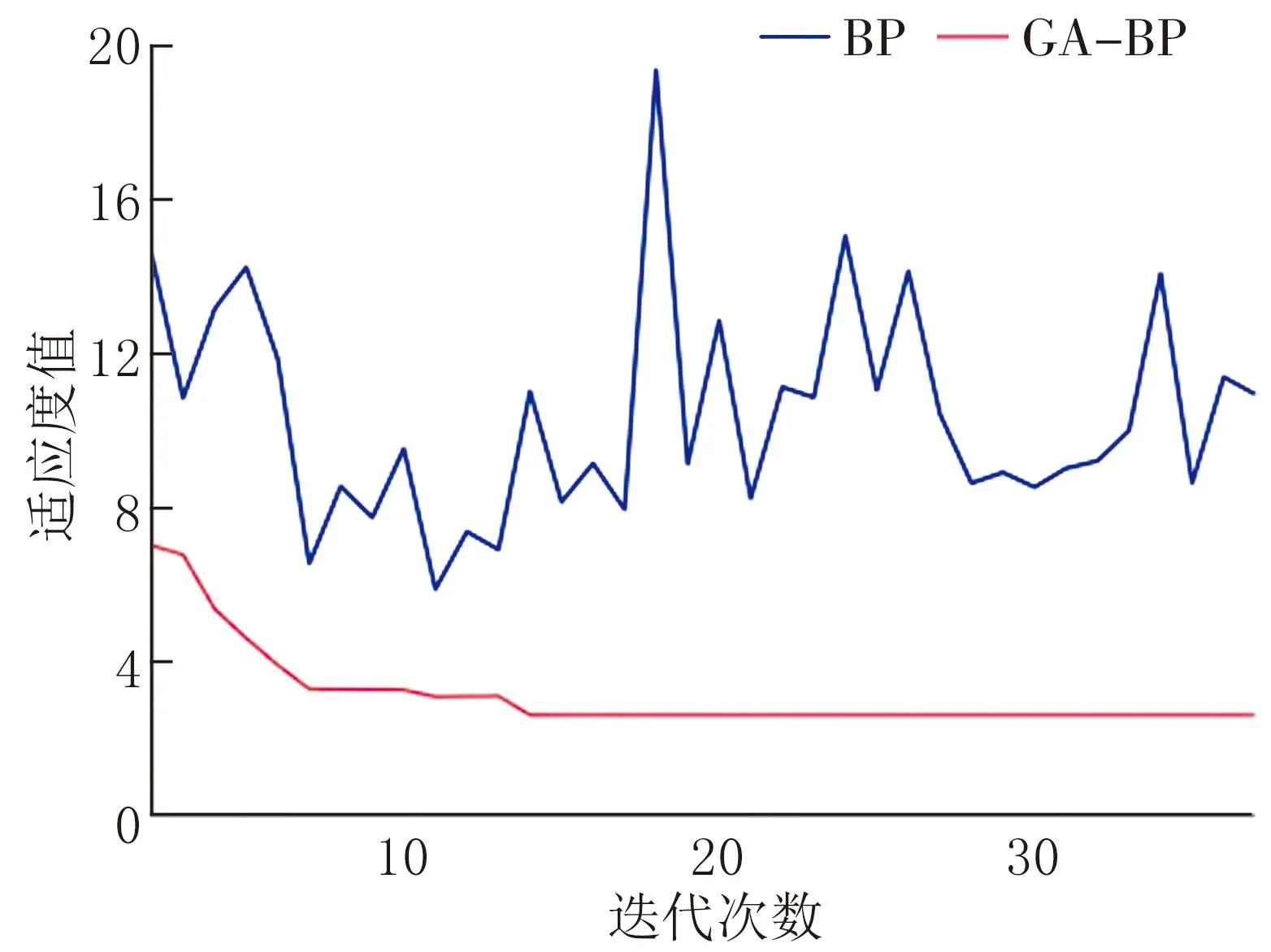
图4 适应度值曲线

2.3 执行遗传操作

搭建GA-BP神经网络适应度曲线的目的在于训练网络得到阈值和权值的最优解。首先对迭代次数,学习率,输入、输出层权值、阈值数据和隐藏层阈值数据进行归一化处理,再将数据重新组合得到的数据以及测试集数据编码作为输入,将最优个体(权值、阈值最优)最优适应度值作为函数的输出,得到的最优个体如图5所示。

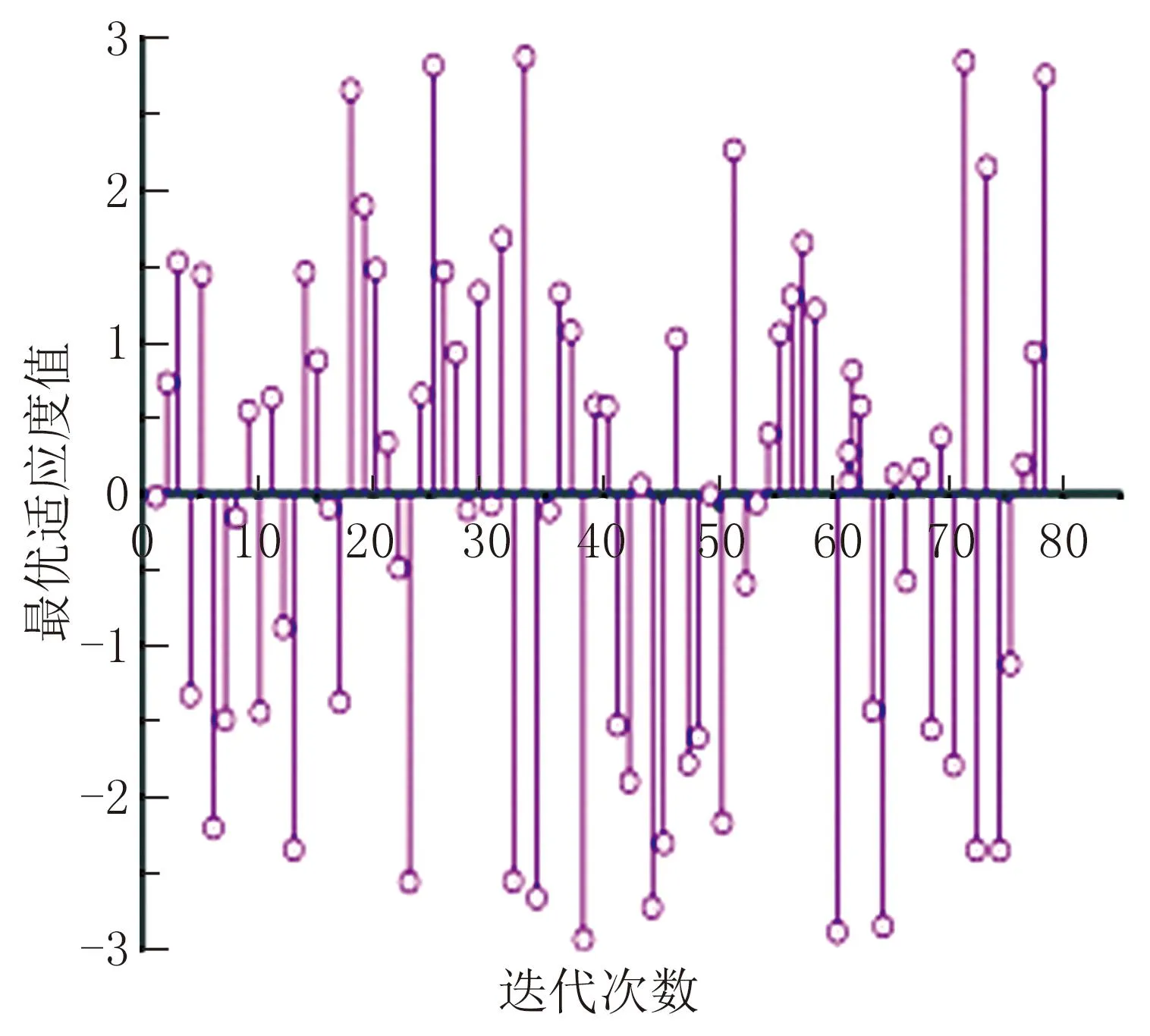
图5 最优个体

对最优个体进行排序,将前40个最优个体作为输入层与隐藏层之间的权值,将第41～55个作为隐藏层节点的阈值,隐藏层至输出层的权值选用第56～70个,输出节点阈值选用第71个,其中将计算所得到的权值及阈值输入至GA-BP神经网络,再进行网络训练,经历连续的训练使得网络最终的权值及阈值最优。GA-BP神经网络最终的最优权值及阈值见表1。

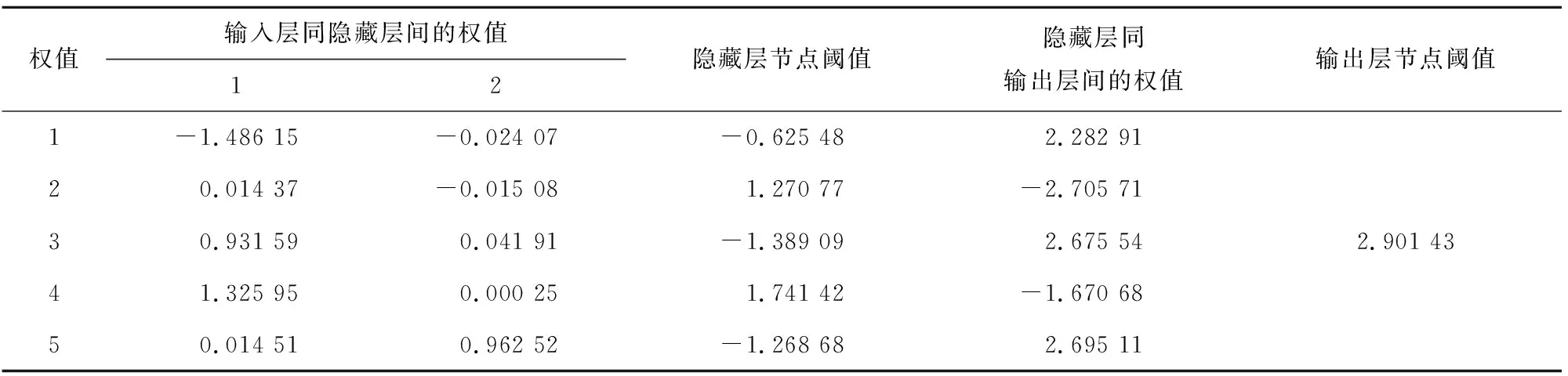
表1 GA-BP神经网络的最优权值及阈值

3 试验设备及数据采集

为了得到大量的试验数据,本文使用了BRUKER摩擦磨损试验机,其通过微机控制步进电机,增添不同模块来模拟磨粒产生的条件,制作特定的磨损粒子,再对仪器制作的磨损图像进行手动分类并备注标签,作为试验的数据集。试验设备参数见表2,磨损试验机如图6所示。

表2 试验所用设备参数

(a)摩擦磨损试验机

(b)旋转驱动

(c)往复驱动

(d) 环块驱动

(e)线性驱动图6 BRUKER摩擦磨损试验机

试验机拥有4种运动模块,可以制作出摩擦、磨损和划痕等多种类型磨损粒子。杰出的模块化设计功能能够同时制作大量磨损粒子样本。由摩擦磨损试验机制作的4种典型粒子图像如图7所示。

(a)氧化磨损颗粒

(b)切割磨损颗粒

(c)疲劳磨损颗粒

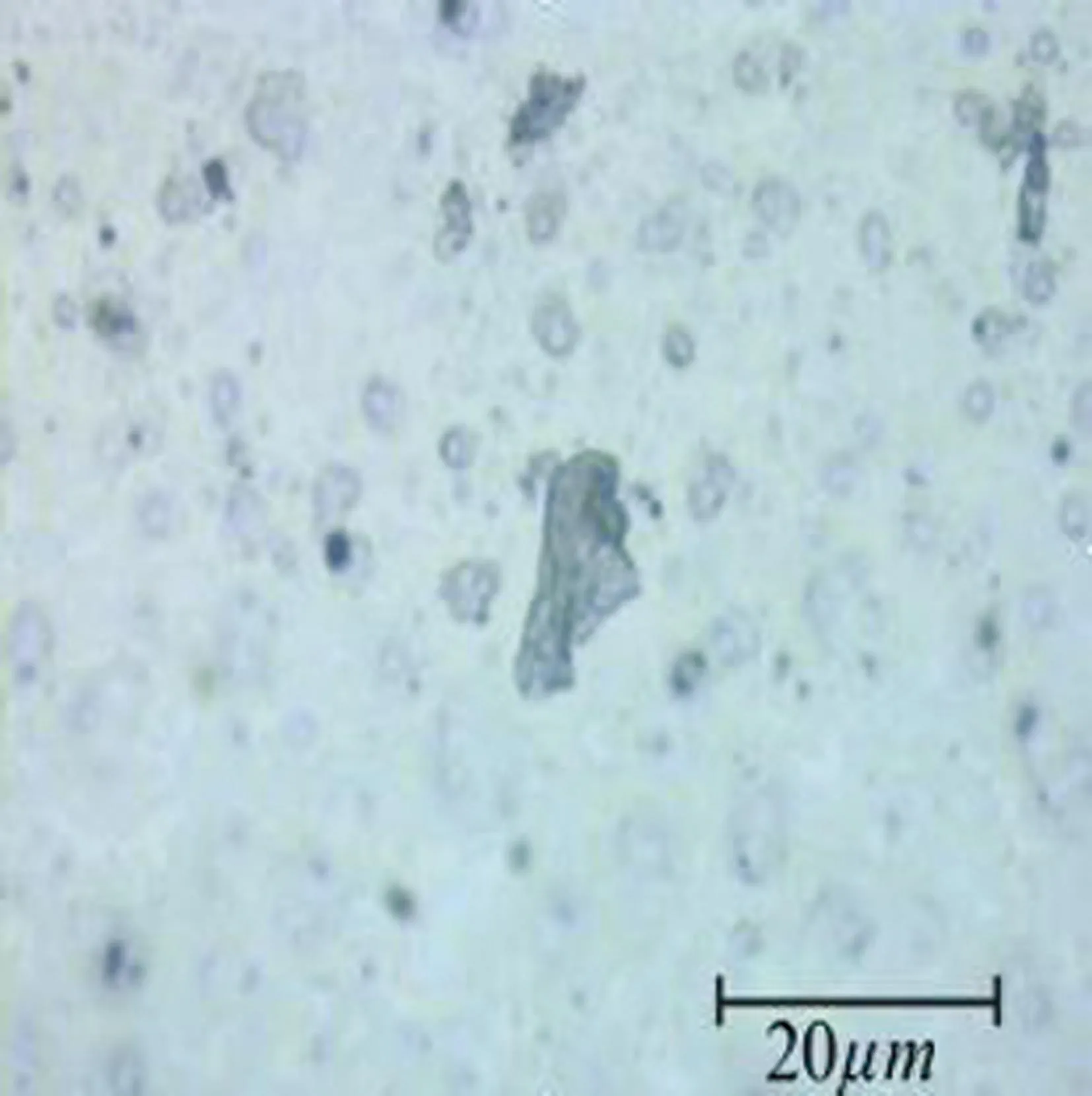
(d)严重滑动磨损颗粒图7 4种典型粒子

由于严重滑动磨损颗粒与疲劳磨损颗粒需要对表面信息进行处理才能将二者区分,本文使用了Contour GT-I 3D光学显微镜,其拥有超强的垂直分辨率,可以扫描500倍的垂直范围,分辨率达到0.01 nm,可以从样品的各个角度获得样品的表面属性,它成像功能极佳,可以对于磨粒表面的信息进行提取处理[7]。

图8 Contour GT-I 3D光学显微镜

4 结果对比与分析

4.1 算法优化对比

在BP神经网络中神经元个数为5和10时,均方误差数量只能达到很低的设定目标,分别为74%和80%,这是因为网络的初始权值、阈值在MATLAB中是随机的,初始值设定不同则网络效率不同,在神经元个数为15和20时,均方误差数量达到预设值,分别为4次和40次,仅达到设定目标的8%和80%,在神经元个数为15和20时,GA-BP神经网络几乎完全达到设定目标,试验数据见表3。

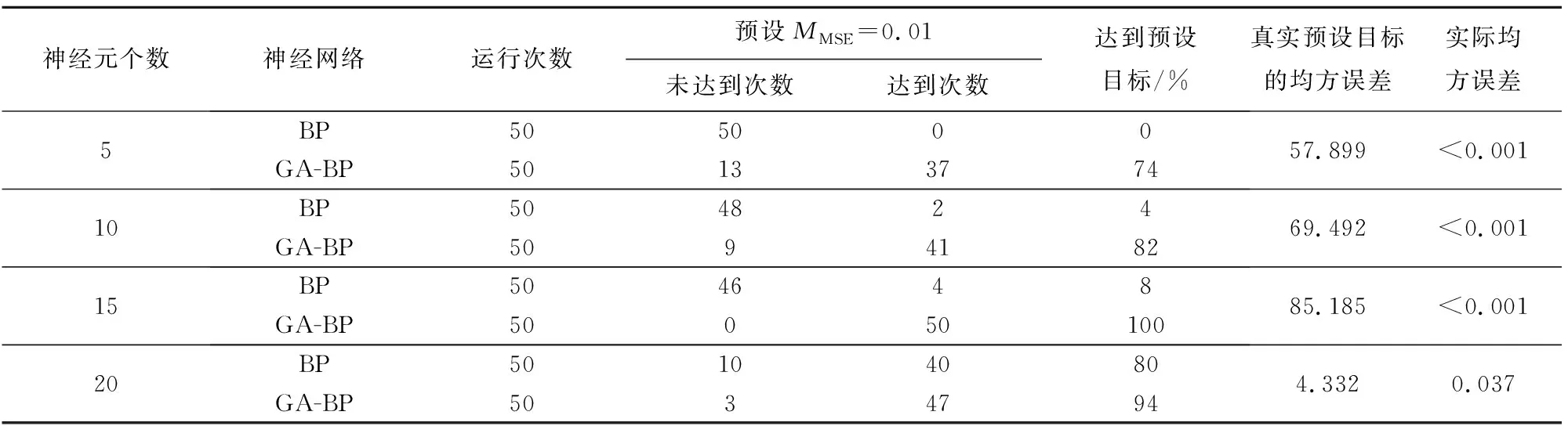
表3 BP和GA-BP的均方误差(MMSE)对比

表3的对比结果表明:随着隐藏层神经元的数量在GA-BP神经网络和BP神经网络中的增加,均方误差达到设定值的数量亦增多,GA-BP神经网络比BP神经网络的数据迭代次数越少,越能够迅速达到设定的MMSE。

决定系数(R2)是评判网络性能的一个重要参考量,其又叫作拟合优度,拟合优度愈大,函数自变量对因变量诠释的水平愈高;相反,拟合程度低则表示自变量与因变量不存在对应关系。因此对应到网络中的解释为拟合优度越高,网络中的输入神经元与输出层阈值联系越紧密。而调整决定系数影响网络输出的精确度。调整决定系数是决定系数的一个调整版本,是用来衡量模型预测能力和拟合优度的指标,本次调整决定系数的方法是增加样本数量。R2和调整R2折线图如图9所示。

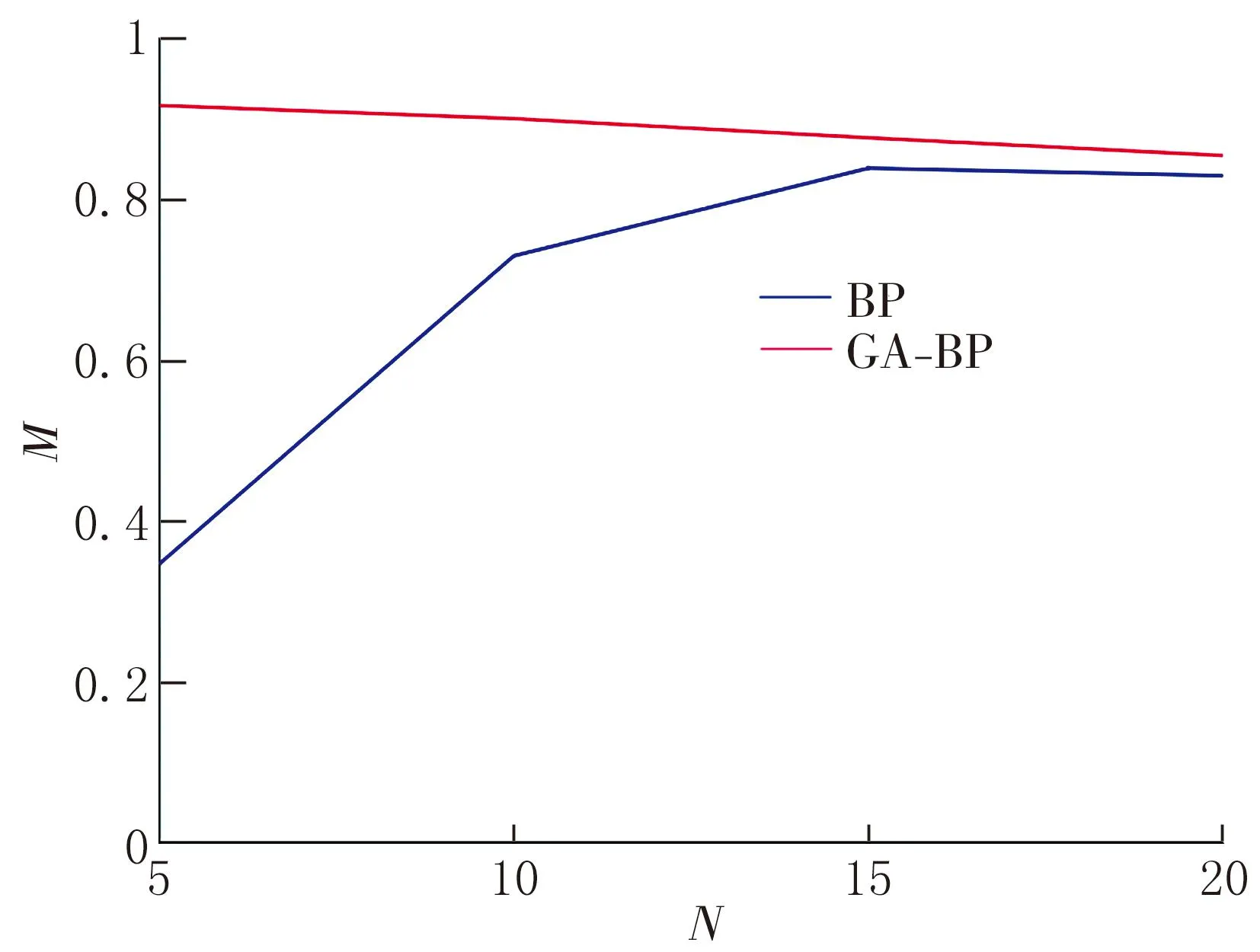
(a)调整R2折线图

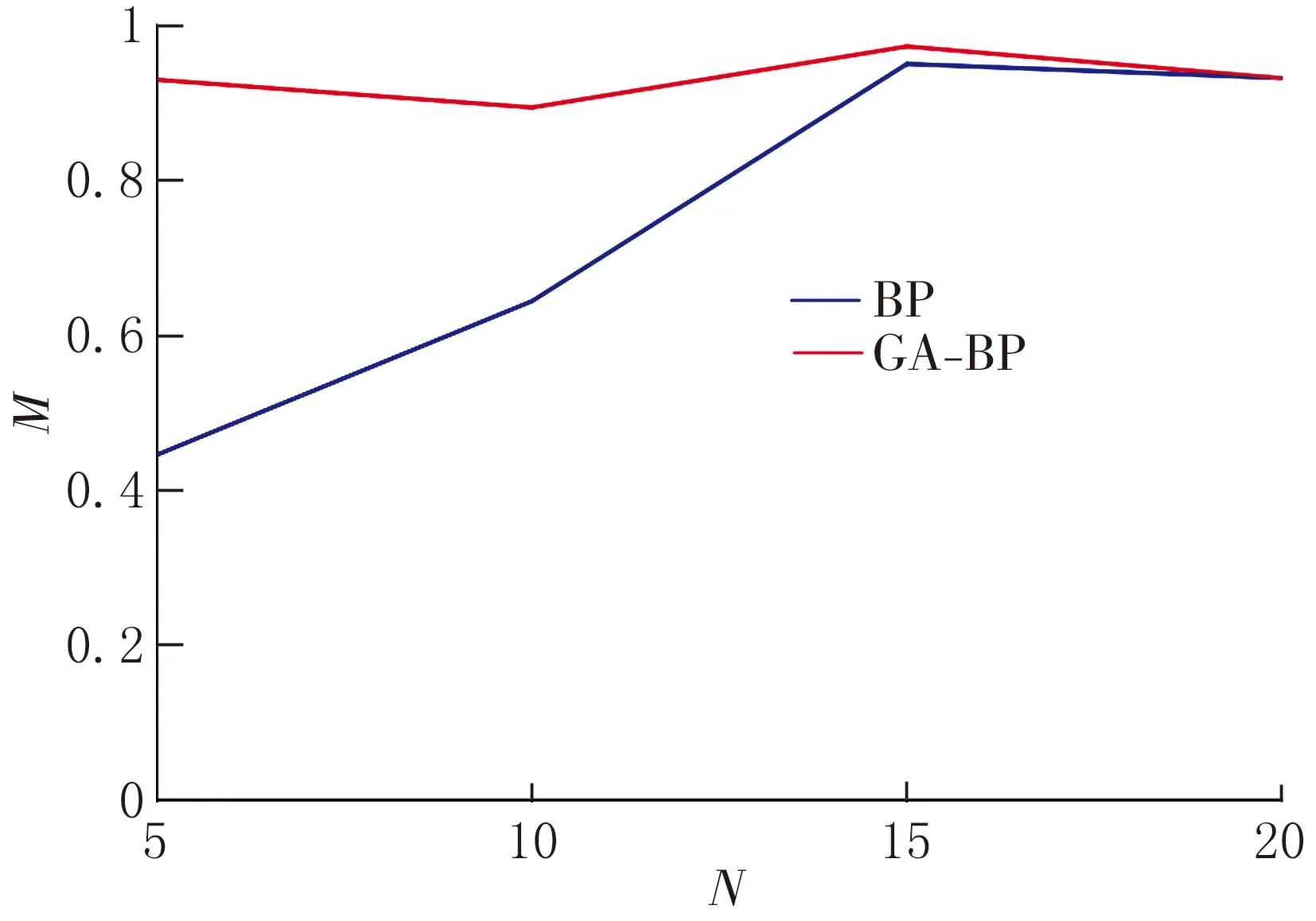
(b)R2折线图图9 BP神经网络与GA-BP神经网络调整R2与R2的对比折线图

从拟合度的角度来说,拟合优度达到0.8就代表拟合效果不错。由图9可知,在隐藏层神经元个数为5、10、15和20时,GA-BP神经网络的调整R2与R2值全部大于BP神经网络对应的调整R2与R2值,表明了GA-BP神经网络比BP神经网络的拟合性能更佳。当隐藏层神经元个数较少时,BP神经网络调整R2与R2值皆≤50%,GA-BP神经网络的调整R2与R2值皆>90%,这说明GA-BP神经网络的性能更平稳。在隐藏层神经元的个数为15时,GA-BP神经网络同BP神经网络的拟合值皆达到最优状态,高达97.2%。

因此选用GA-BP神经网络对数据进行拟合预估分析更合理。

4.2 试验结果分析

把汽车4S店维修厂以及试验室制作的500张磨粒图片作为训练样本,为了防止试验结果过拟合,将图片进行旋转、切割、翻转和增加亮度等操作[8],随机选取其中未扩展的250张图片作为训练集对BP神经网络进行训练,其中氧化磨损颗粒90张,切割磨损颗粒30张,圆形磨损颗粒50张,严重滑动颗粒20张,疲劳颗粒60张。将剩下未扩展的250张磨粒图片进行数据集增广,拓展为1 075张,作为试验集图片。再对GA-BP神经网络初始化加入最优权值、阈值,将试验集图片的训练结果画出混淆矩阵图(混淆矩阵图被称为误差图,目的是反映试验模型的准确率(Accuracy)和召回率(Recall)),如图10所示。

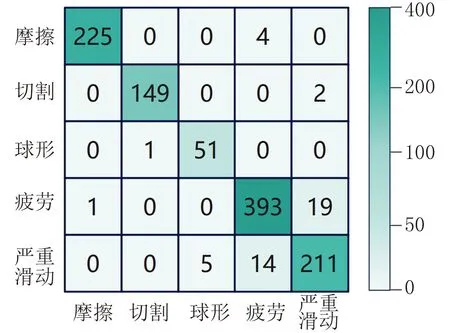
图10 GA-BP神经网络对汽车润滑系统磨粒分类的混淆矩阵图

由图10可知,改良后的BP神经网络对磨粒分类的准确率(Accuracy)已经达到试验所需的标准,网络对氧化磨损颗粒、球形磨损颗粒以及切割磨损颗粒几乎做到能识别,部分测试集图片上含有多种磨粒信息,试验集的图像在几何特征以及表面信息方面与真实磨粒极为相似,在不同的磨粒图片上的分类出现叠加。

在GA-BP神经网络建成后,将数据集分为试验集和训练集,由训练集确定GA-BP神经网络隐藏层中的各个参数阈值,再用添加参数后的网络对试验集图像进行分类,将这个模型迭代100次,并将其学习率设置为0.01,其中准确率(Accuracy)及学习损失率(Loss)能够直接反映出该模型的优劣[9]。将数据整理做出GA-BP神经网络的准确率和损失率折线图,如图11所示。

(a)GA-BP的准确率

通过试验训练可以看出,GA-BP神经网络的准确率曲线呈收敛状态,网络的损失率很快下降,并在一段时间后逐渐趋于平缓,证明GA-BP神经网络是能够对磨粒进行分类的。而且GA-BP神经网络的学习速度快,数据收敛迅速,准确率高达96.92%。试验结果表明,本文提出的方法在磨粒分类方面有较好的表现,满足磨粒分类的准确性和汽车润滑系统工作效率的双重需求。