不同参数下的庞加莱晶体性质比较

王能正, 王 沛

(浙江师范大学 物理与电子信息工程学院,浙江 金华 321004)

0 引 言

超冷原子气体[1]是量子模拟的重要平台,可被用来模拟一些难以在固体材料中实现的多体模型.利用光晶格技术[2-3]可以在冷原子平台上实现人造晶体,引入随时间周期变化的势场还能够实现格点之间的次近邻跃迁、次次近邻跃迁等,从而制造出具有非平凡拓扑性质的能带模型.利用Floquet工程虽然可以有效模拟格点之间的短程跃迁,但模拟长程跃迁仍然较为困难.理论和实验技术的发展为解决这一问题提供了思路,光晶格中的数字微镜[4-5]或亚波长技术[6-8]能够在单格点尺度上调节势场形状,从而实现势能函数的可编程性.在这一技术的基础上,二次型量子傅里叶变换(quadratic quantum Fourier translation,QQFT)协议利用哈密顿矩阵在动量空间的对角性,提出了通过傅里叶变换来模拟不规则长程跃迁的方案.QQFT拓展了冷原子平台的模拟范围,令长程跃迁模型的实验实现成为可能.

庞加莱晶体[9]是一类具有不规则长程跃迁的模型,该模型源自量子力学中对称原理的应用.探索具有新奇对称性的模型是物理学长期以来的目标.100多年前,晶体的离散空间平移对称性成为布洛赫能带理论的基础;近年来,时间晶体[10-11]、Floquet拓扑绝缘体[12-13]等理论把离散平移对称的应用从空间拓展到了时间领域;最近,研究者进一步提出时空晶体[14]的概念,1+d维时空内的时空晶体具有d+1个相互独立的离散平移对称轴,时空晶体这一概念不但丰富了人们对晶体对称性的认识,也对新对称群下的拓扑物态分类提出了挑战.另一方面,洛伦兹对称也是一种时空对称,其对称操作会把时空坐标混杂在一起.洛伦兹对称性是量子场论、标准模型的基础,但它在凝聚态物理中却鲜有应用,原因之一在于洛伦兹变换的长度收缩效应会改变晶格常数,从而与晶体的离散平移对称性相抵触.但是,最近的研究表明,如果时间与空间同时具有离散平移对称性,那么洛伦兹变换有可能维持晶格常数不变,在这一基础上,具有洛伦兹对称性的时空晶体模型被构造出来,即庞加莱晶体.理论研究表明,利用QQFT协议可以实现庞加莱晶体,并且其实现方案具有一定的抗噪声能力[15].

庞加莱晶体具有多个可调节参数,包括洛伦兹变换的特征元、晶体尺寸等.到目前为止,并无解析方法判断一个时空晶体模型是否具有洛伦兹对称性,相反,只能通过数值方法逐个构造模型来寻找可能的庞加莱晶体.之前的研究列举了所有特征元等于2同时格点数小于100的1+1维庞加莱晶体,发现在这些模型中粒子波函数的传播表现出规则的回声结晶化性质,这与一般晶体中波函数的传播性质完全不同.在这一背景下,本文系统研究了不同参数下的庞加莱晶体模型,发现这些模型都一致表现出回声结晶化性质,说明该性质受到洛伦兹对称性保护.笔者的研究加深了对庞加莱晶体性质的理解.

1 庞加莱晶体理论简介

(1)

对称群P是一个离散庞加莱群,它是量子场论中的庞加莱群的子群.

这里需注意的是：式(1)中的洛伦兹变换矩阵是在笔者选择的T,a,c的表达式下给出的,因此,其形式和选择光速c=1情况下的对称矩阵不同,但其本质都是洛伦兹变换.另外,式(1)给出的变换P(j,m,n)具有不变性,这一点可从下述性质看出：首先,P(j,m,n)是庞加莱变换的一种特殊情形,因此,庞加莱变换具有的不变性P(j,m,n)都具有;其次,若t,x取整数,则变换后的t′,x′也必然取整数,反之也成立,这说明晶格本身在P(j,m,n)变换下保持不变;最后,取2个不同的P变换做乘积,易知结果也是一个P变换,因此,P变换本身满足对称群的乘法闭合性.

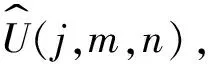
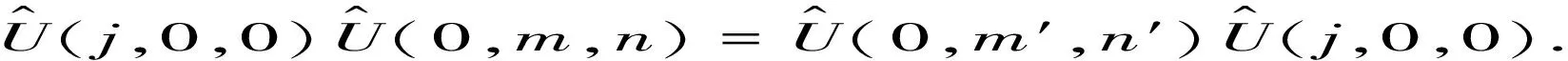
(2)

将式(2)作用于准动量能量空间|E,k〉可得到

(3)

上列等式可转为这样一个色散关系,

2πl+m′TE′-n′ak′=mTE-nak.

(4)

(5)

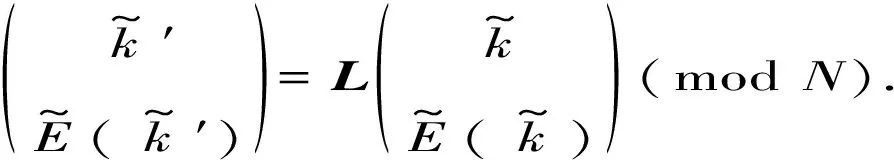
(6)

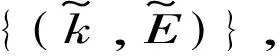
值得注意的是,虽然本文使用了色散关系这一术语,但实际上庞加莱晶体模型是有限N模型,并且函数E(k)的形式依赖于N的值,不存在N→∞的极限.事实上,洛伦兹不变的E(k)是不连续、不规则的,与过去所熟悉的格点模型色散关系完全不同.另外,当说一个庞加莱晶体是单能带时,指每个k对应唯一一个准能量E,在实空间内,这意味着每个元胞只包含1个格点,并且格点无内部自由度.

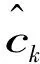
(7)

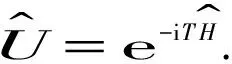
庞加莱晶体的传播子具有洛伦兹对称性,这一性质把它和普通晶体区分开来.为了更清楚地观察模型的离散庞加莱对称性,可以计算推迟格林函数Gr,以此来验证它在时空演化下的洛伦兹不变性.假设在初始时刻,一个粒子被置于格点j上,经过时间mT后粒子处在格点j+n,在此传播过程下,Gr可表示为

(8)

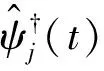
2 高γ值庞加莱晶体

2.1 γ=3的色散关系

之前的工作列举了γ=2的1+1维庞加莱晶体,在这里继续研究了一些高γ值的情况,分别是γ=3,γ=4及γ=5.首先考虑γ=3的庞加莱晶体的理论性质,根据式(1)和式(6),γ=3的单粒子色散关系的洛伦兹不变性可以表示成

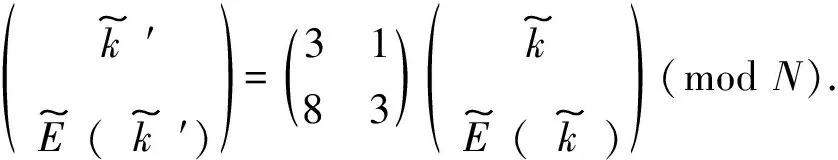
(9)

式(9)仅在N取某些特定值时有解.发现50以内合适的N值包括：N=2,4,6,7,8,12,14,16,17,18,23,24,28,31,32,34,36,41,42,46,47,48,49.对于大部分N,洛伦兹不变色散关系不是唯一的,这里选择了N=18这一晶体长度做出了相应的色散关系(E(k)-k)图像.其中γ=3的色散关系E(k)比γ=2在长度为18的情况下的6组E(k)有更多的选择.图1(a)和图1(b)为γ=3时的2组色散关系E(k),这里的色散关系集合满足E(k)=2π/T-E(2π/a-k),可以看到色散关系图像呈现不规则的锯齿形状,与γ=2的色散关系形状不同[9],锯齿形E(k)相对于k=π/a或E=π/T不对称,但它在左右两边1/4处各自对称,即连续2次映射回k=π/a和E=π/T.因此,它们总是成对出现(E′(k)=E(2π/a-k)和E″(k)=2π/T-E(k)都是洛伦兹不变量).

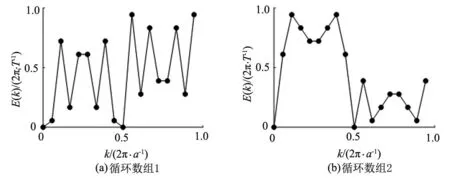
图1 γ=3的色散关系图(格点数N=18)

2.2 γ=3的Floquet有效哈密顿量

接着研究Floque有效哈密顿量的相关性质.其中实空间哈密顿量可以写为

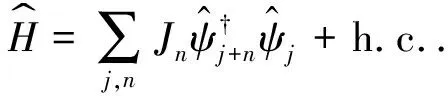
(10)

图2 γ=3的跃迁系数函数Jn(格点数N=18)

2.3 γ=3的单粒子传播子性质

在γ=2条件下具有离散庞加莱对称的时空晶体表现出周期性的回声性质.接下来对于高γ值模型的推迟格林函数Gr进行相应的验证.在γ=3的情况下,考虑初始时刻位于n=0格点处的单粒子,其推迟格林函数在时间和空间的演化下用Gr(m,n)表示,其中m表示时间(周期T为单位),n表示空间位置(或格点数),并且m和n都取整数.对称性质由矩阵L表征,它要求(m′,n′)T=L(m,n)T时,有

Gr就是庞加莱晶体中自由电子的传播子,该传播子和自由时空中电子的传播子不同,依赖于庞加莱晶体的具体色散关系.Gr是一个N项之和,一般情况下,它不存在一个简单的解析表达式,只能通过具体数值计算得到.

(a)系统尺寸为18的图像

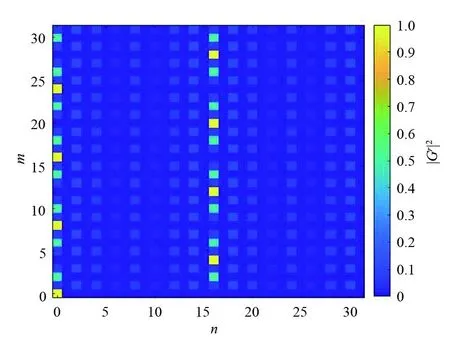
(b)系统尺寸为32 的图像

2.4 γ=4,5的庞加莱晶体

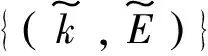
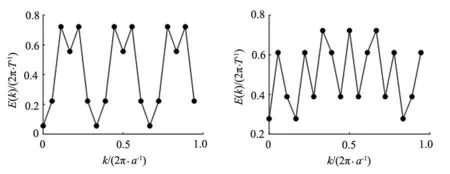
(a)γ=4,N=18 (b)γ=5,N=18

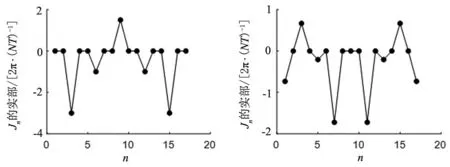
(a)γ=4,N=18 (b)γ=5,N=18

3 总 结

在本文中,首先简要回顾了一维晶格上具有离散庞加莱对称性的量子理论.离散庞加莱P包含离散洛伦兹变换和离散时空平移,后者在t-x平面上形成Bravais晶格.P的元素用幺正算子表示.平移的共同特征态被定义为具有确定的准动量k和准能量E的单粒子态.群的乘法定律决定了E和k如何在离散的洛伦兹推动下变换,得到色散关系E(k).根据多体理论推出有效哈密顿函数H,H依赖于E(k).通过计算推迟格林函数对洛伦兹不变性进行检验,它表示庞加莱晶体在不同位置和时间之间的相关性.

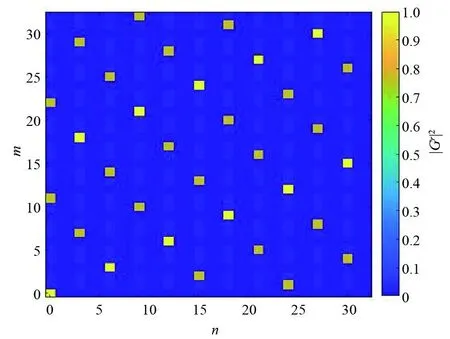
(a)在γ=4下系统尺寸为33的图像

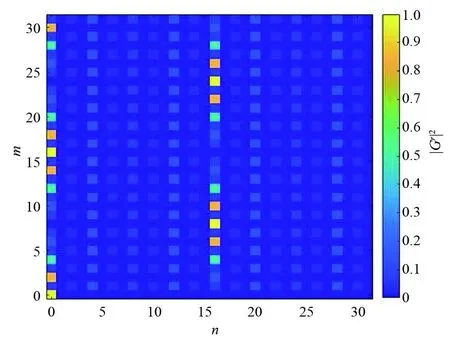
(b)在γ=5下系统尺寸为32的图像