基于机器学习的盾构掘进参数预测

熊英健，贾思桢，刘四进，杜昌言，历朋林

(1.西南交通大学交通隧道工程教育部重点实验室,成都 610031; 2.中铁十四局集团大盾构工程有限公司,南京 211800)

引言

盾构法施工具有适应性强、施工快速安全、对周围环境影响小的优点,已成为城市地铁施工的首选方法。我国在大直径盾构制造和应用方面持续取得突破性进展,推动地铁建造朝着更大断面的方向发展。

在盾构机施工过程中,盾构掘进参数的设置往往由盾构司机依照自身经验进行操作,这不利于保证施工效率和施工安全。若盾构掘进参数设置不当,易引发掌子面失稳、盾构掘进姿态不良、刀具磨损、刀盘结泥饼等诸多问题。目前,众多学者也就此展开了相关研究。王洪新等[1]基于模型试验结果,建立土压平衡盾构掘进的数理模型,并推导出总推力、土仓压力、螺旋机转速、掘进速度间关系的数学表达式。徐前卫[2]通过试验得出了推进速度、螺旋机转速和刀盘开口率等主要盾构施工参数与土层特性之间的适应性联系。江华等[3]推导了盾构推力的理论计算公式,得到了盾构推力与刀盘开口率成反比,盾构推力与渣土的内摩擦角成正比的结论。张志奇等[4]针对盾构掘进速率与刀盘扭矩进行多元回归分析,得到适用于复杂地层的掘进参数回归模型。李杰等[5]建立了盾构掘进速度的参数模型,得到了复合地层下盾构掘进速度的最优化掘进参数。于云龙等[6]建立标准推力-标准力矩修改特征空间,修正了传统盾构掘进速度模型。

近年来,由于大数据和人工智能技术大发展,越来越多的学者使用机器学习的方法预测盾构掘进参数,并取得了较好的预测结果。李超等[7]采用BP人工神经网络方法建立了复合地层条件下盾构掘进参数的预测模型。李港等[8]发现考虑数据时间相关性的LSTM模型比随机森林模型对TBM的总推力和刀盘扭矩体现出更好的预测能力。黄靓钰等[9]建立了可输出盾构掘进速度、推力等掘进参数的BP神经网络水下岩溶盾构掘进参数预测模型。罗维平等[10]通过网格搜索方法以及5折交叉验证法进行模型超参数调整,建立了盾构切口泥水压力的随机森林预测模型。范文超等[11]建立基于BP神经网络的复合地层超大直径泥水盾构掘进参数预测模型,定量预测刀盘转矩、刀盘能耗和平均泥水压力。仉文岗等[12]将4种常见的超参数优化算法与随机森林预测模型相结合来预测TBM的掘进速度,发现使用贝叶斯优化能以最短的耗时及最高的精度完成对掘进速度的预测。张哲铭等[13]以原始数据中均匀提取的样本、RBF核函数和10 折交叉验证建立的LS-SVM模型可以较为准确地预测稳定段中的刀盘扭矩、刀盘推力、总推力、推进速度。HOU等[14]为提高有限元数据下盾构掘进参数匹配的准确性,提出了基于支持向量机(SVM)和指数调整惯性权重免疫粒子群优化(EAIW-IPSO)的匹配模型。WANG等[15]通过降噪分析、互相关分析 (CCA)和长短期记忆 (LSTM) 网络相结合,使用隧道参数和地质数据作为输入来预测隧道掌子面泥水压力。LIN等[16]发现主推力、贯入度、泡沫量和注浆量与推进速度有很强的相关性,并且发现所有智能模型的性能都优于经验方法。SHI等[17]提出了一种结合变分模式分解(VMD)、经验小波变换(EWT)和长短期记忆(LSTM)网络的新型混合多步预测模型,用于预测盾构机刀盘扭矩,并取得了95%以上的准确率。

目前,针对盾构掘进参数的预测模型在划分数据集时多采用先随机打乱数据再划分训练集与测试集的方法,这种做法不可避免地会导致在测试集中的数据受到原数据集中与其相邻的且又被划分到训练集中的数据影响。此外,许多对掘进参数的预测分析也未考虑地层物理力学参数的影响。故依托济南市济泺路穿黄隧道工程,在划分数据集时考虑施工先后顺序,并从土体的粗细程度、软硬程度、密实程度和渗透能力4个维度对土体物理力学性质进行描述,考虑土体分布对掘进参数的影响,使用LSTM模型、随机森林模型与BP神经网络对盾构的总推力和掘进速度进行预测,为盾构在相似地层中掘进时提供参数选取和建立模型的参考。

1 工程背景

济南市济泺路穿黄隧道工程位于济南市天桥区,起点位于黄河南岸老城济泺路与泺口南路交叉口以南约300 m,向北依次下穿二环北路、绕城北高速高架、南岸大堤、黄河、北岸大堤,鹊山村,后接现状国道G309。济泺路穿黄隧道工程被誉为“万里黄河第一隧”,是国内在建最大直径的盾构隧道,也是黄河上第一条公路地铁合建的隧道。工程线路走向见图1。

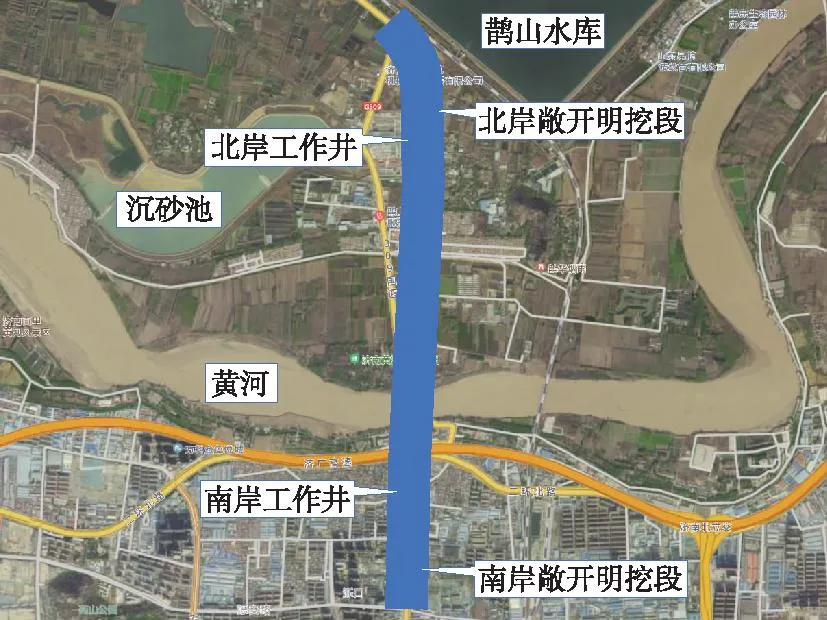
图1 济南市济泺路穿黄隧道线路走向Fig.1 The route direction of the Yellow River Tunnel on Jiluo Road in Jinan City

济泺路穿黄隧道工程采用泥水平衡盾构施工。盾构机最大掘进速度为45 mm/min,最大回缩速度为1 600 mm/min。盾构机的推进系统布置了56个油缸,最大推力为199 504 kN。盾构刀盘为常压进仓式刀盘,开口率约为50%,最大工作压力为7.5 bar。刀盘开挖直径为15.74 m,最大超挖量为50 mm。刀盘的额定扭矩为37 594 kN·m,脱困扭矩为50 751 kN·m,转速为2 rpm。

隧道盾构段断面净空如图2所示。管片外径为15.20 m,内径为13.90 m,分为上下两层,上层为三车道层,下层则分成四仓,分别是轨道交通、烟道、纵向逃生通道和管廊。

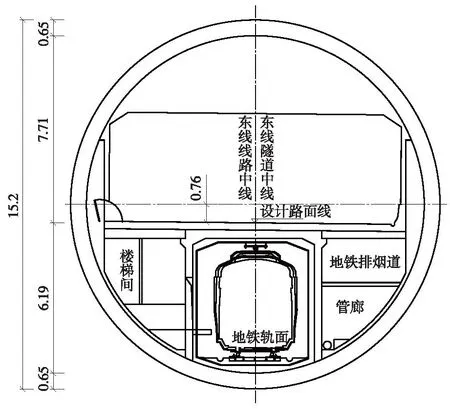
图2 盾构净空断面(单位:m)Fig.2 Clearance section of shield (unit: m)

盾构隧道东线地层断面如图3所示。盾构区间最小覆土厚度11.2 m,仅为0.73倍洞径,土体受施工扰动敏感。盾构段围岩以黏性土为主,局部为砂层及钙质结核层,表层为粉土,地下水与黄河河水联系较为密切,盾构施工时砂层可能发生大的渗透变形破坏;局部粉质黏土中结核含量高,富集成层,掘进过程会面临半软半硬地层,可能发生盾构机抬头、偏移或被卡住、蛇行推进等现象。因此,选择合理的掘进参数对降低盾构掘进过程中发生事故的概率至关重要。

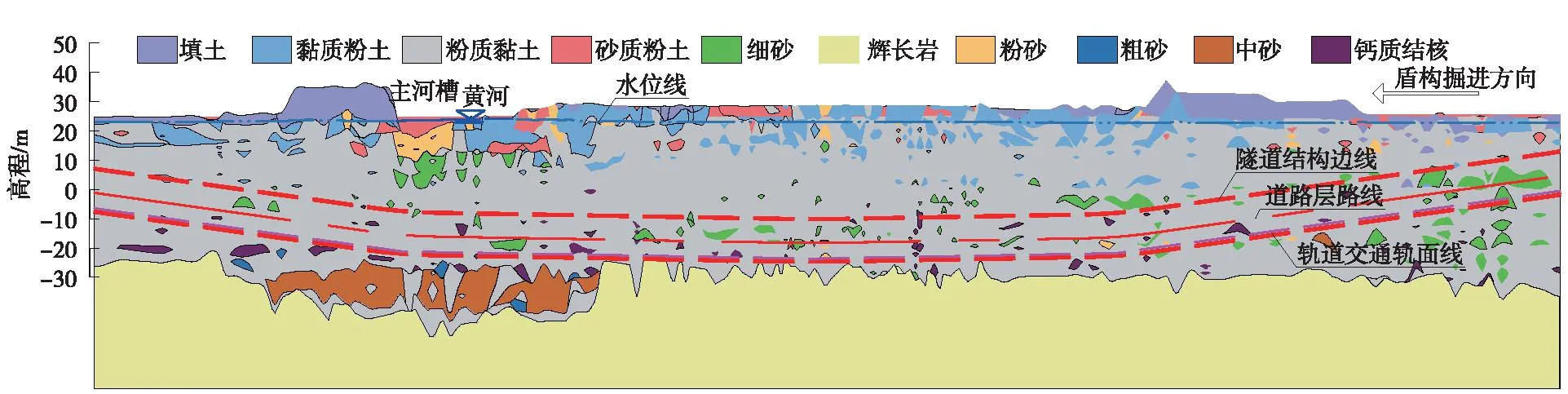
图3 盾构隧道东线地层纵断面(单位:m)Fig.3 The stratum longitudinal section of the east line of shield tunnel (unit: m)

2 预测模型原理

2.1 LSTM模型原理

长短期记忆模型(Long-Short Term Memory,LSTM)[18]能够使用门控制器来有效处理循环神经网络面临的梯度衰减和梯度爆炸问题。信息在各个长期记忆单元间的流动由LSTM模型中的输入门(It)、输出门(Ot)和遗忘门(Ft)来控制。LSTM单元结构图如图4所示,其中LSTM的输入为Ct-1、Ht-1和Xt,输出为Ct和Ht。Ct-1和Ht-1分别为上一时间步的记忆细胞和隐藏状态;Xt为当前时间步的输入;Ct和Ht分别为当前时间步的记忆细胞和隐藏状态。

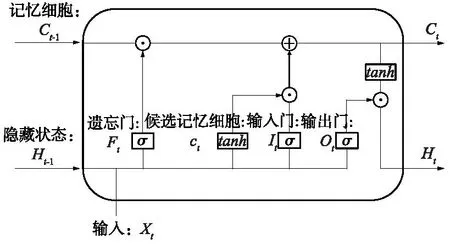
图4 LSTM单元结构Fig.4 LSTM unit structure

输入门、遗忘门和输出门计算公式如下所示。

It=σ(XtWxi+Ηt-1Whi+bi)

(1)

Ft=σ(XtWxf+Ht-1Whf+bf)

(2)

Ot=σ(XtWxo+Ht-1Who+bo)

(3)

(4)

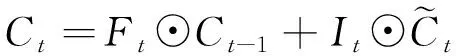
(5)

隐藏状态Ht计算公式如下所示。

Ht=Ot⊙tanh(Ct)

(6)

式中,Wxi、Wxf、Wxo、Wxc和Whi、Whf、Who和Whc为权重参数;bi、bf和bo、bc为偏差参数;σ、tanh为激活函数;⊙为按元素乘法,而不是矩阵乘法。

2.2 随机森林模型原理

在机器学习中,随机森林是属于集成学习中的bagging算法(Bootstrap aggregating,引导聚集算法)。这是一种基于大量决策树的算法,采用bootstrap重抽样方法从数据集中随机选择多个子样本,并且将每个决策树都在子样本上进行训练。当决策树的每个节点需要分裂时,使用某种策略随机从子样本的众多属性中选择一个属性作为该节点的分裂属性,持续此步骤直至不能再分裂为止。这样就建立了大量的决策树,构成了随机森林。最终预测结果将通过对所有树的概率预测求平均值确定。随机森林因其众多的优点而成为最为流行的机器学习模型之一,例如:(1)即使面对高维度的数据也不需要降维和特征选择;(2)通过feature importance可以判断特征的重要程度;(3)通过降低结果的方差,可以有效避免过拟合。随机森林模型见图5。

图5 随机森林模型Fig.5 Random forest model

2.3 反向传播(BP)神经网络原理

BP神经网络是一种监督式的学习方法。BP神经网络的结构组成包括输入层、隐含层和输出层,输入层与输出层的节点个数分别为输入参数个数与输出参数个数。隐含层个数与隐含层节点个数是决定BP神经网络预测精度的重要因素。在确定隐含层的节点个数时,如果节点个数太少,则将导致训练过程中出现欠拟合的情况,而节点个数太多,不仅会导致训练过拟合,还会增加训练时间。隐含层层数与隐含层节点个数主要根据预测精度不断调整[19]。模型结构如图6所示。

图6 BP神经网络结构Fig.6 BP neural network structure

BP神经网络的运算过程包括2个部分。首先是前向传播部分,在输入样本后,输入数据从输入层经过隐含层到输出层。当隐含层的输入为xi时,则当前隐含层的输出值yi计算式则如下

(7)

式中,sigmod为激活函数;wij为节点的连接权重;bij为节点阈值。

然后是反向传播部分,使用反向传播算法对神经网络的权重和阈值进行训练优化,试图使输出结果与预期结果的差距尽可能小。重复以上的运算过程对权重和阈值进行训练,当输出误差的平方和小于指定值时停止训练,并且保存此时神经网络的权重和阈值。

3 工程应用

3.1 数据预处理

随着盾构机的掘进,大量的掘进参数被实时输出,选取济南市济泺路穿黄隧道工程的参数进行分析。对泥水盾构机来说,主要的掘进参数有掘进速度、刀盘转速、刀盘扭矩、总推力、切口水压等。除了盾构机输出的掘进参数,土层参数和几何参数也对盾构的总推力和掘进速度产生较大影响。常见的土层参数有隧道上覆土体加权密度、土体含水量、内摩擦角等。常见的几何参数有隧道埋深、隧道洞身围岩所处断面的地下水位与断面直径等。

3.1.1 异常数据处理

济南黄河隧道东线原始数据每10 s采集1次,研究段的原始数据2 741 984组,掘进参数2 816个,由于盾构设备在掘进过程中会出现不稳定的数据波动,因此,在对数据进行分析前,需要将某些异常点进行剔除。

首先,选取掘进状态下的盾构掘进数据,剔除每个操作段内前10%的数据,避免盾构启动时的数据波动影响[20]。接着,对每环掘进状态下,所有时间步的数据求均值,剔除偏差幅度之和最大的一组数据再求均值并剔除偏差数据,如此反复,每环保留90%的数据,并以此求出均值作为该环的一组数据。最后,使用拉依达准则对数据进行处理,若某环数据距离均值大于3倍标准差,则剔除该环。

在对数据处理中发现,当盾构掘进到黄河大堤附近时,掘进参数出现大量的“异常数据”,此处的“异常数据”是因为特殊工程地质产生的真实值,故不对其剔除。

经过数据清洗后,提取出1 130组(环)数据,盾构关键掘进参数18个。

3.1.2 筛选输入数据

隧道几何参数:由于断面直径为常数,为考虑断面直径的影响,故选取隧道埋深H与断面直径D的比值深跨比H/D作为几何参数。

工程地质参数:由于本工程为穿黄隧道,因此水位线高度作为输入参数。在考虑地层对掘进参数的影响时,为准确描述土体的物理力学状态,采用了4个维度来描述,分别是土体的粗细程度、软硬程度、密实程度和渗透能力;其中,粗细程度用粒径大小区分,软硬程度用液性指数区分,密实度用标准贯入击数区分,渗透能力用渗透系数区分。对开挖面内的粗细程度、软硬程度、密实程度和渗透能力按照不同土层所占面积进行加权平均。4个维度的等级标准如表1所示。

表1 地层物理力学参数Table 1 Physical and mechanical parameters of strata

盾构施工参数:施工参数选取掘进用时、平均轴线偏差、刀盘扭矩、掘进速度、总推力、刀盘转速、切口水压、气泡仓压力、盾尾油脂量、HBW油脂消耗量、EP2油脂消耗量、进浆比重、出浆比重、进浆流量、出浆流量、注浆量、盾尾间隙最大值和盾尾间隙总值。在预测相应的输出参数时将剔除输入参数中的该项。

为提高模型的运算速度,使用皮尔逊相关性系数(Pearson correlation coefficient)对盾构施工参数进行筛选。对所有盾构施工参数进行两两分析,选取与预测参数皮尔逊系数大于0.2的参数作为输入参数。若输入参数间的皮尔逊相关系数大于0.9,则剔除其中一项[21]。

皮尔逊相关系数是度量两个变量间相关程度的有效手段,其值介于-1与1之间。皮尔逊相关系数公式如下

(8)

借助热力图可以清晰地反映变量间的相关性,如图7和图8所示,图中相关性系数较大的呈现深色,相关性系数较小的呈现浅色。

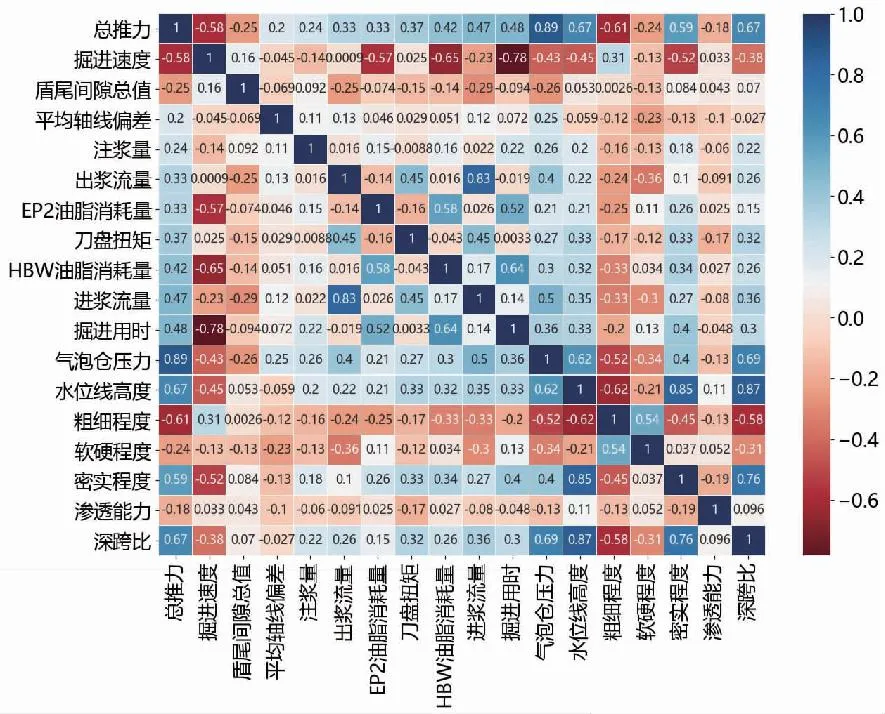
图7 总推力与输入参数的热力图Fig.7 Heat diagram of total thrust and input parameters

图8 掘进速度与输入参数的热力图Fig.8 Heat diagram of tunneling speed and input parameters

总推力作为输出参数时筛选出17个输入参数,其中气泡仓压力与总推力极强相关,水位线高度、深跨比、粗细程度与总推力强相关,渗透能力与总推力则是极弱相关。

掘进速度作为输出参数时筛选出15个输入参数,其中掘进用时、HBW油脂消耗量与掘进速度为强相关,渗透能力、软硬程度与掘进速度则是极弱相关。

3.1.3 数据标准化

为减小不同输出参数量纲和尺度差异的影响,提高拟合精度和速度,在建立模型之前采用标准化方法对训练集数据进行处理。计算公式如下

(9)

3.2 评价指标

为评估模型的拟合程度和预测效果,采用均方误差(MSE)最小时的模型对训练集进行评估,并使用平均绝对百分比误差(MAPE)、均方根误差(RMSE)和平均绝对误差(MAE)对测试集的预测结果进行评价,计算公式如下

(10)

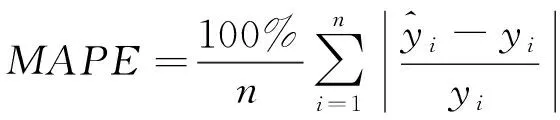
(11)

(12)

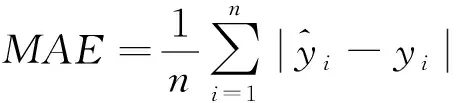
(13)

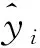
3.3 确定超参数

超参数是指在模型训练前或者训练中人为调整的参数。当验证集的MSE最小时,选取此时的参数组合作为模型的超参数。

在搭建LSTM模型时,结合使用一维卷积层(Conv1D)处理长序列,因为它能利用卷积核对特征进行提取,学习保留有用的信息,而只删除不重要的细节。卷积层常与池化层(Pooling层)相结合,对特征稀疏处理,减少数据运算量。LSTM模型的网络结构设定为1个输入层、1个一维卷积层、1个Pooling层、2个LSTM隐含层、1个Flatten层、1个Dense层、1个Dropout层(Dropout=0.5)和1个输出层。使用Flatten层将多维的输入一维化,便于和后续的全连接层进行连接。

在模型训练过程中,将模型的迭代次数Epoch、一维卷积层单元数Unit、LSTM隐含层单元数Units_1与Units_2、学习率Lr作为待寻超参数,对其搜索寻优,其余参数采用默认值。LSTM模型的超参数如表2所示。

表2 LSTM模型的超参数Table 2 Hyperparameters of LSTM model

随机森林模型的超参数亦使用搜索寻优确定,采用10折交叉验证算法对模型的超参数进行确定。在训练集中,将数据分为10组,每次从中随机抽取1组数据作为验证集,并对剩下9组数据进行训练,重复训练和验证过程10次,每次都使用不同的验证集进行验证,最后取10次验证集的表现进行平均得到最终的MSE。随机森林模型的超参数如表3所示。

表3 随机森林模型的超参数Table 3 Hyperparameters of random forest model

在构建BP神经网络时,将其网络结构设定为1个输入层(激活函数为sigmod)、1个隐含层、1个Dropout层(Dropout=0.5)和1个输出层。优化器设置为Adam。

目前使用BP神经网络对盾构掘进参数预测的文章,所使用的计算隐含层节点的经验公式自变量少有考虑训练样本数量的影响。故采用以下经验公式对隐含层节点数量进行计算。

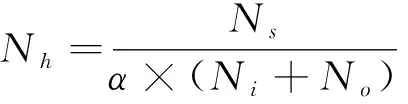
(14)

式中,Nh为隐含层节点数;Ns为训练集样本数;Ni为输入层节点数;No为输出层节点数;α为2～10范围内的常数。

超参数的选择可以反映模型的特点,LSTM模型的迭代次数小于BP神经网络,尽管LSTM的模型复杂度大于BP神经网络,但小的迭代次数反映了LSTM较小的模型计算成本;对于随机森林,决定其精度主要与n_estimators(决策树的数目)有关;对于BP神经网络而言,3层神经网络可通过调整节点个数逼近任意复杂度的连续函数,且满足精度要求,故本文仅建立了一个隐含层[22]。BP神经网络的超参数如表4所示。

表4 BP神经网络超参数Table 4 Hyperparameters of BP neural network

3.4 建立预测模型

首先将数据预处理后的1 130组数据按照施工先后顺序以8∶2的比例分为训练集和测试集,其中随机森林模型与BP神经网络的训练集打乱顺序,而LSTM模型的训练集不做处理。在训练集中训练确定模型,并在测试集中评估预测参数和实际参数的误差。预测模型的流程如图9所示。

图9 预测模型流程Fig.9 The process of prediction model

将训练集中1/10的数据划分为验证集,验证集中的误差如表5所示。

表5 LSTM模型、随机森林模型和BP神经网络的均方误差(MSE)Table 5 Mean square error (MSE) of LSTM model, random forest model and BP neural network

由表5可知,对于总推力预测精度:LSTM>BP神经网络>随机森林;对于掘进速度预测精度:BP神经网络> LSTM>随机森林。BP神经网络的平均误差最小,除总推力的误差略大于LSTM模型之外,掘进速度的误差显著小于另外两个模型,这与BP神经网络的迭代次数有关;LSTM总推力模型精度最高,这与其节点神经元数量最大有关;随机森林模型总推力和掘进速度的误差在3种模型中都是最大的,并且其需要调整的超参数多,搜索范围广。

3.5 模型预测结果与分析

对测试集的226组数据进行误差分析,对应环号范围为990～1 241环。对总推力和掘进速度的预测结果如图10～图15所示。

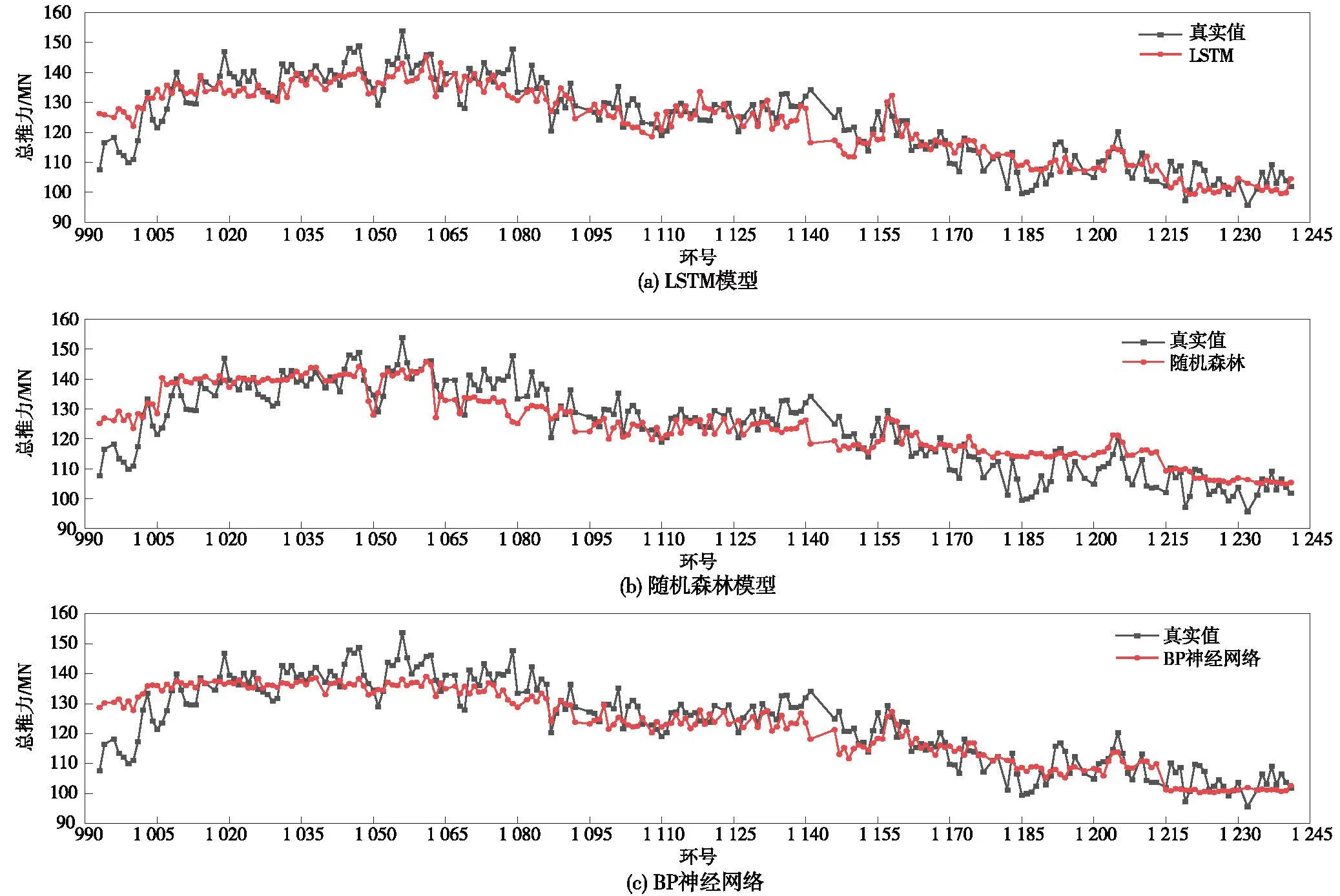
图10 总推力预测结果Fig.10 Prediction results of total thrust

由图10可见,3种模型对总推力的预测均取得了不错的预测效果,预测值曲线与真实值的曲线吻合程度颇高,特别是LSTM模型,在曲线波动剧烈的区间内还能保持着较小的误差。3种模型预测总推力的相对误差如图11所示。

图11 预测总推力相对误差Fig.11 The relative error of predicted total thrust

由图11可见,3种模型大部分误差都控制在10%以内,且误差趋势在1 180环之前大致相同。在1 180～1 220环范围内,随机森林模型的预测误差与LSTM模型和BP神经网络的预测误差相差较大,并且有多个环的随机森林模型预测相对误差超过10%。3种模型的相对误差占比如图12所示。

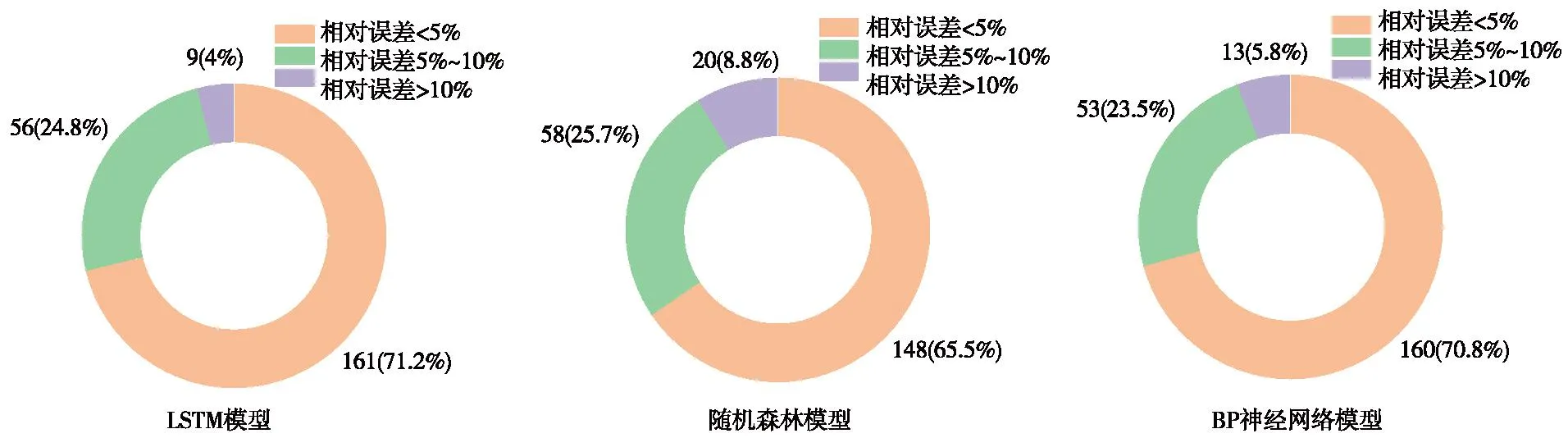
图12 总推力相对误差占比Fig.12 The relative error proportion of total thrust

通过对3种模型相对误差都大于10%的环段结合纵断面图进行分析,发现993～1 005环处于黄河主河槽向大堤过渡段,1 079环附近为泺口险工向地面过渡段,土压均变化急剧;1141环附近环段内受到北绕城高速高架桥桩基的影响;1 182环附近遇到了黏质粉土与钙质结核。说明模型对总推力预测出现较大误差主要是地形的剧烈变化导致的。为减小盾构在穿越桩基时地表沉降,适当增大掘进工作面的推力[23]及盾构机的总推力[24],可将预测值扩大5%～10%。在土压急剧变化时,预测值偏激进,即土压增加,预测值偏大,土压减小,预测值偏小,可减小或扩大预测值5%～10%以减小误差。

对掘进速度的预测结果如图13～图15所示。

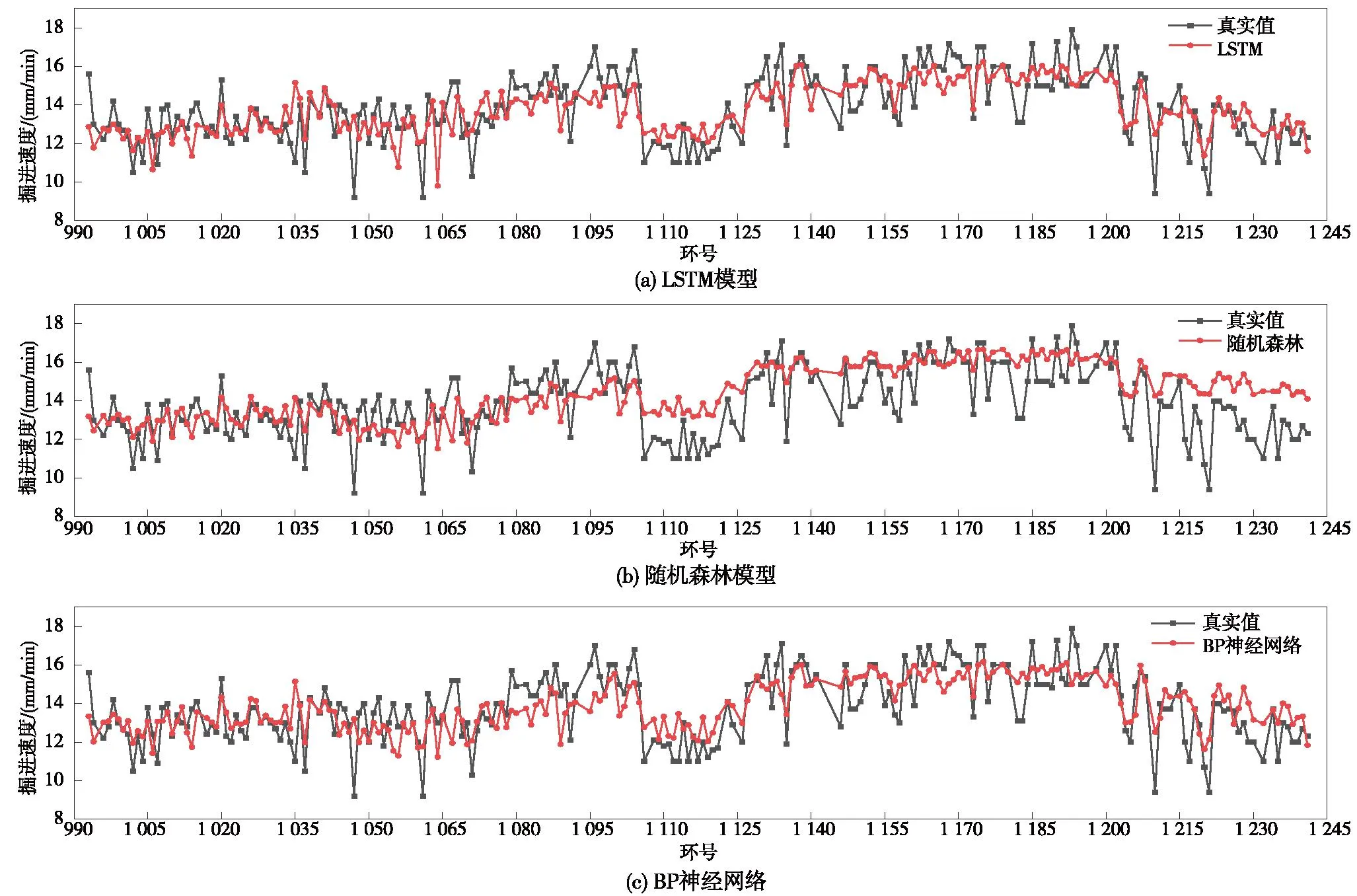
图13 掘进速度预测结果Fig.13 The relative error of predicted tunneling speed

由图13可见,LSTM模型和BP神经网络对掘进速度的预测取得了不错的效果,预测曲线与真实曲线吻合程度较高,而随机森林模型对小部分环段的曲线吻合有一些偏差。相对误差如图14所示。

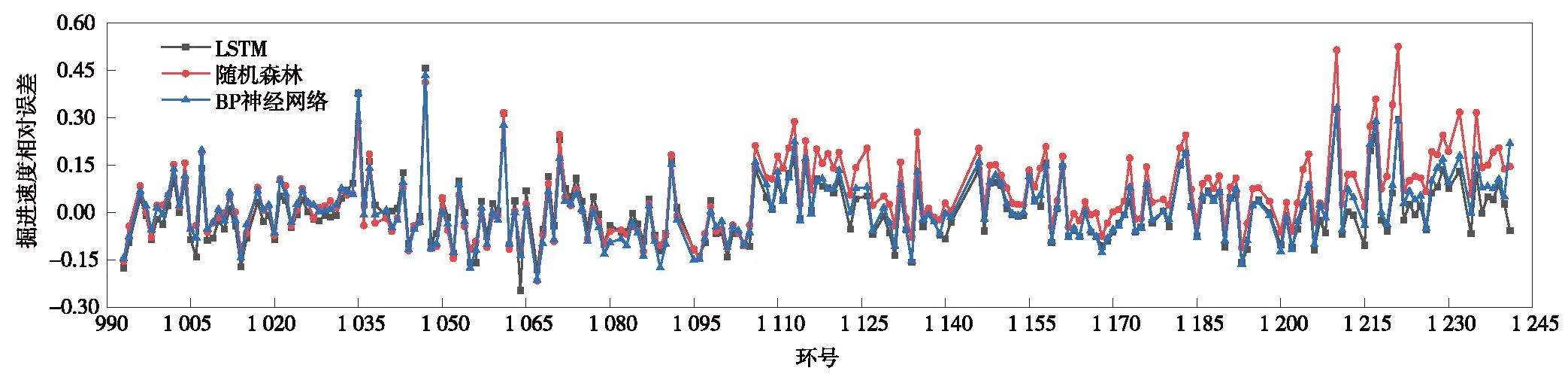
图14 预测掘进速度相对误差Fig.14 The relative error proportion of tunneling speed

由图14可见,LSTM模型与BP神经网络大部分的误差都控制在15%以内,且误差趋势大致相同。随机森林模型的预测误差较大,有多个环的相对误差超过15%。3种模型的相对误差占比如图15所示。

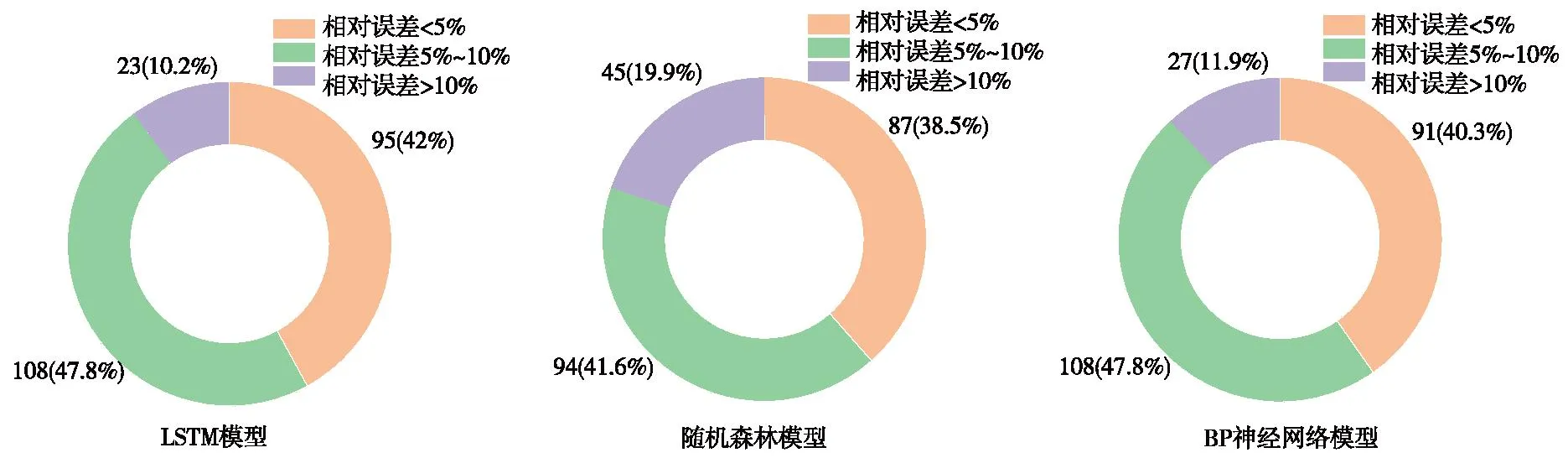
图15 掘进速度相对误差占比Fig.15 The relative error proportion of tunneling speed

通过对3种模型相对误差都大于15%的环段结合纵断面图进行分析,发现1 035～1 047环段为黄河大堤段向泺口险工段过渡段,此段水压急剧下降,掌子面内及刀盘附近存在钙质结核;1 061～1 071环与1 210～1 221环盾构处于直线与平曲线过渡段。说明对掘进速度预测产生较大误差主要受地形与线路变化的影响。受平曲线影响,掘进速度会略有降低[25],可对预测值减小15%～20%以缩小误差。

基于测试集的数据,LSTM模型、随机森林模型和BP神经网络对总推力和掘进速度的评价指标数值分别如表6和表7所示,3种模型的训练耗时如表8所示。

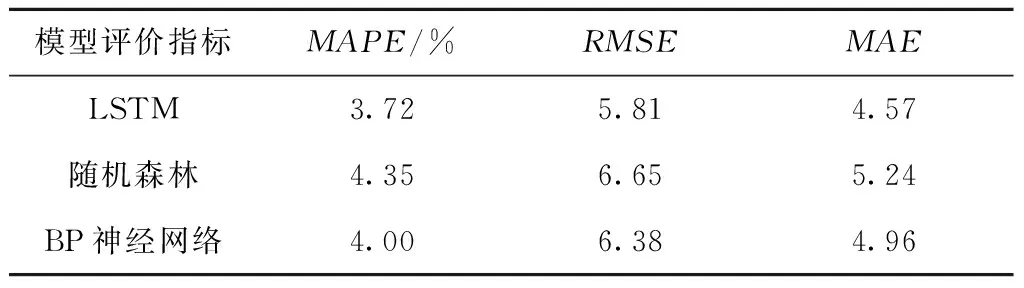
表6 总推力预测结果Table 6 Prediction results of total thrust

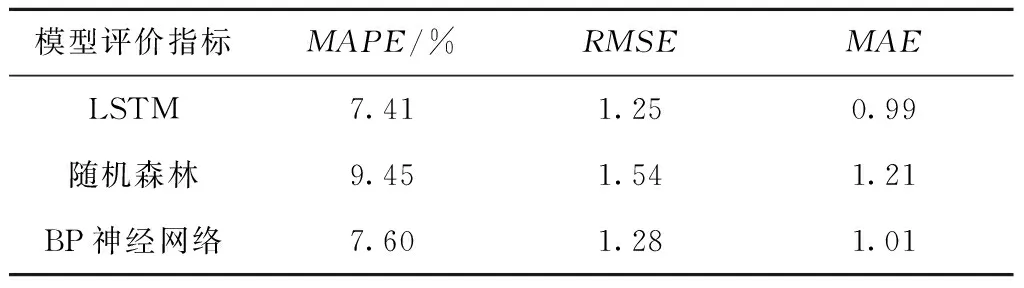
表7 掘进速度预测结果Table 7 Prediction results of tunneling speed

表8 模型训练耗时 sTable 8 Training time of the model

在MAPE、RMSE和MAE三个评价指标中,RMSE对异常点的敏感程度要大于MAPE和MAE,即如果模型在某点处的预测值误差较大,会对RMSE的值有较大影响。同时,由于RMSE和MAE的误差大小与实际值的量纲和尺度有关,故仅对其在不同模型预测同一掘进参数时进行比较。MAPE在考虑预测值与真实值的误差之上,还考虑了误差与真实值之间的比例,其值越小,说明预测模型的精确度越高。

由表6可知,LSTM模型预测总推力的精确度显著高于另外两个模型,并且它在异常点处的预测值误差也偏小。随机森林模型的误差在3种模型中最大,并且在异常点处的预测值误差偏大。BP神经网络的预测精度则处于两者之间。

由表7可知,LSTM模型预测掘进速度的精准度最高,异常点外的误差小。BP神经网络的精准度略低于LSTM模型,但显著高于随机森林模型。

由表8可知,在训练模型方面,随机森林模型的训练时间最短,平均训练时间在4 s以内,优于LSTM模型并且显著优于BP神经网络,这是由于后两者的迭代次数过多导致的。

由表6～表8可知,LSTM模型的预测效果最好,符合施工精度要求,并且模型训练耗时在可接受范围内;BP神经网络的预测效果中等,但其训练时间过长;随机森林模型虽然训练时间短,但其预测效果却不如前两者。

4 结论

依托济南市济泺路穿黄隧道东线工程,按照施工顺序划分数据集,采用4个维度描述土体的物理力学状态,建立了基于LSTM模型、随机森林模型和BP神经网络的预测模型,定量预测盾构机总推力和掘进速度,得出以下主要结论。

(1)LSTM模型在按照施工顺序预测总推力和掘进速度时,平均相对误差仅为3.72%和7.41%,精准度高,误差小,模型训练时间均在20 s以内,时间成本较低,整体表现优于随机森林模型和BP神经网络,特别是在预测总推力时,其效果十分显著。BP神经网络存在计算精度较低、时间成本高昂的缺点。经综合考虑,在预测盾构总推力和掘进速度时应选择LSTM模型。

(2)在地形地貌发生剧烈变化以及盾构掘进线路在直线与平曲线过渡时,盾构的总推力以及掘进速度将发生较大波动,此时文中使用的3种模型都出现了较大的偏差,其中LSTM表现最好,预测结果相对误差偏大的组数仅占4%与10.2%,并且总体平均误差不超过10%,满足施工要求。

(3)随机森林模型虽然训练时间短、总体误差基本满足施工要求,但其预测结果的相对误差在总推力和掘进速度出现剧烈波动的环段处偏大,并且数量偏多,因此在按施工顺序对总推力和掘进速度预测时不是优选。