基于FAPSO的地铁列车节能运行优化研究

黄江平，郑帅沁

(华东交通大学电气与自动化工程学院,南昌 330013)

引言

城轨列车以其安全、舒适、环保、运输能力强等特点,在交通运输中扮演了越来越重要的角色。然而,伴随着列车运量的增加,其能源消耗也在不断增加[1]。根据现有城市轨道交通运营数据统计,列车的牵引能耗约占整个城市轨道交通系统能耗的50%[2]。因此,研究降低列车运行过程中的牵引能耗,对城市轨道交通可持续发展具有重要意义。

国内外学者针对列车运行过程中的驾驶策略优化问题已展开了深入研究和探索,期待获得更好的节能运行策略,以实现列车节能、准点运行的目标。HOWLETT等[3]对多坡度线路的列车节能运行优化问题进行研究,首先将线路分段并使用局部最小值原理计算坡道线路上全局最优策略的工况转换点,为列车节能运行提供指导。ALBRECHT等[4]提出了一种基于最优控制理论和梯度法的两级算法,在满足列车节能运行的同时,使列车运行过程中工况转换次数最少。SONG等[5]以高速列车节能运行为研究目标,通过采用双速度曲线优化方法对实际速度曲线进行优化。FENG等[6]从列车牵引节能和提高运输效率的角度,以定量方式优化高速列车目标速度,通过对比分析出不同站间距离下列车运行应具有的目标速度。HU等[7]总结了列车节能控制的典型模型和算法,提出了基于并行计算结构模型的改进粒子群优化算法,用来搜索列车的节能运行控制策略。杨辉等[8]以站间运行的能耗和时间的权衡为目标函数,构建列车运行能耗、运行时间与惰行点的RBF神经网络模型,采用遗传算法寻优惰行点,最终确定列车节能、正点运行的速度曲线。金则灵等[9]针对城轨列车节能运行的问题,将列车运行状态离散化,以时间和能耗作为奖励函数,采用Q学习算法优化列车控制策略;刘晓飞等[10]提出了一种基于模拟退火(SA)改进粒子群优化算法来求解列车节能运行工况转换速度序列及位置的坐标点,从而获得列车节能运行的最低能耗值。张惠茹等[11]以列车能耗值和列车时刻表稳定性综合最优为目标,构建列车节能控制的时刻表优化模型,通过采用迭代寻优的富余时间分配求解算法,优化列车运行时刻表,减少列车运行能耗。何之煜等[12]针对高速列车在多站间运行中的节能优化问题,基于列车运行时刻表对冗余时间分配策略进行研究,通过合理分配冗余时间,优化列车运行时刻表,降低列车运行能耗。

虽然国内外学者对列车节能运行问题展开了深入研究,然而在列车运行模型构建和运行策略选择上存在一些不足。例如,为简化分析大多采用单质点模型,不能准确分析列车运行过程所受附加阻力的变化情况;另外,大多研究将列车运行时刻表与列车运行策略单独分析,而实际上同一条运行线路,不同站间运行时间对列车运行策略和运行能耗也会产生较大影响;同时,同一运行区间下,采用不同的驾驶策略也会影响列车运行能耗。

综上所述,针对地铁列车节能运行优化研究,在以往研究的基础上构建多质点列车运行能耗模型,以列车运行时间和运行能耗作为优化目标,采用萤火虫-粒子群优化算法(FAPSO)将列车运行时刻表与列车运行策略通过双层结构一体化优化,为各区间筛选出最优驾驶方案,最终实现列车节能、准点运行的目标。

1 地铁列车运行模型构建

1.1 列车动力学模型

在列车运行过程中,施加牵引力能够使列车向前运动并克服运行过程中的阻力;施加制动力能够调节列车运行速度或使列车停车,且列车制动产生的再生制动能量可供同一供电区间内的其他列车使用。目前针对列车动力学建模主要有单质点建模和多质点建模两类[13]。其中,单质点模型将列车视为单一质点,把列车运行过程中所受力均集中在该质点上分析计算,忽略了列车内部和车厢之间的作用力,导致列车在运行过程中遇变坡点或变曲率点时所受附加阻力跳变,这与附加阻力实际变化情况存在一定差距。而多质点模型是将列车的每一节车厢都当作一个独立的质点[14]。因此,相比于单质点模型,构建多质点模型能够充分考虑列车整体受力情况,列车经过变坡点或变曲率点时能够准确分析计算列车所受附加阻力,对列车的运行过程描述更贴近实际,列车多质点模型如图1所示。不同模型下列车运行过程中所受附加阻力如图2所示。

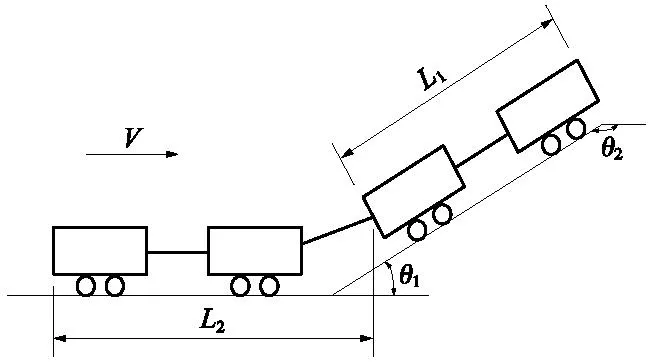
图1 列车多质点模型Fig.1 Train multi particle model

图2 不同模型下附加阻力变化Fig.2 Changes in additional resistance under different models

1.2 列车运动学方程

对列车运动过程进行受力分析,由牛顿第二定律有

(1)

(2)

式中,a为加速度;s为站间距离;F为牵引力;B为制动力;F0为基本阻力;F附为附加阻力;M为列车质量;γ为回转质量系数,通常取0.06。其中,按TB/T 1407.1—2018《列车牵引计算规程》,多质点模型下对附加阻力分析计算如式(3)所示。

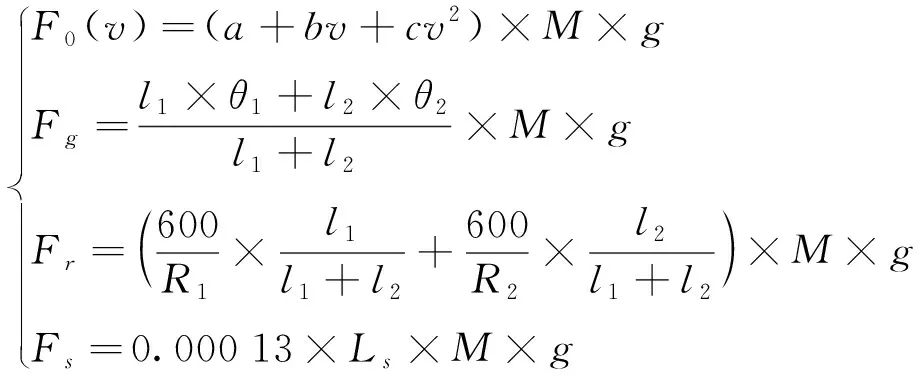
(3)

式中,a、b、c为常数,不同车型常数取值不同;g为重力加速度,取9.8 m/s2;Fg为坡道附加阻力;θ1、θ2分别为运营线路的坡度角;Fr为列车在弯道上运行时受到的曲线附加阻力;R1、R2分别为第1、2段曲线上的半径;l1、l2分别为列车处于第1、2段曲线上的长度;l1+l2为列车总长度;Fs为隧道空气附加阻力;Ls为隧道长度。

1.3 列车能耗模型构建

目前,地铁列车大多装有再生制动设备,当列车处于制动状态时会反馈能量到车载储能设备或接触网中,因此,构建列车运行能耗模型时,牵引列车向前运动产生的牵引能耗和由列车制动产生的再生制动能量要分开计算,最终计算出的列车运行能耗即牵引能耗和再生制动能量两者间的差值,如式(4)所示。

(4)

式中,E1为输出能量,即由牵引列车向前运动产生的牵引能耗;E2为输入能量,即由列车处于制动状态时产生的再生制动能量;s1为列车制动起始点;s2为站间终点;η、α分别为牵引效率和再生制动能量反馈效率。同时,为保证列车安全、准点、舒适运行,列车在运行过程中还应满足各项约束条件,因此建立的多站间列车运行能耗模型如式(5)、式(6)所示。

(5)

(6)

式中,En为第n站间列车运行能耗;x为列车站间数量;vs0、vs2分别为运行列车初速度、末速度;v(s)lim为路段限速;Tn为各运营区间的计划时间;Tts为列车站间停站时间,本文假设列车停站时间仍为时刻表所设定的;T总为总计划时间;Δt为允许的时间偏差。

2 包含萤火虫算子的粒子群优化算法

在处理非线性问题时,标准粒子群优化算法(PSO)寻优过程比较复杂,收敛速度慢、效率低[15],且在寻优过程中易陷入局部最优的情况。因此,为平衡种群粒子的全局搜索与局部搜索能力,提高算法搜索精度与速度,在标准粒子群算法的基础上,引入萤火虫算子对标准粒子群算法进行优化,构建一种包含萤火虫算子的粒子群优化算法,即FAPSO。

在标准粒子群算法中,惯性权重w控制着算法的搜索能力,因此,合理的惯性权重取值,有利于提高算法的搜索精度和速度,避免寻优过程中陷入局部最优的情况。因此,在标准粒子群算法的基础上,引入萤火虫算法中的吸引度算子β[16],如式(7)、式(8)所示。在文献[17]的基础上,对标准粒子群算法中惯性权重系数重新设计,其表达式如式(9)所示。

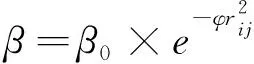
(7)

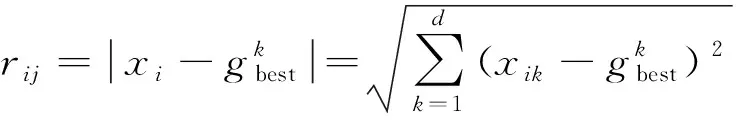
(8)

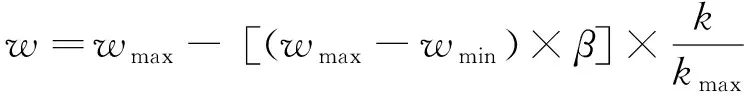
(9)

算法优化后种群粒子速度和位置更新公式如式(10)所示。

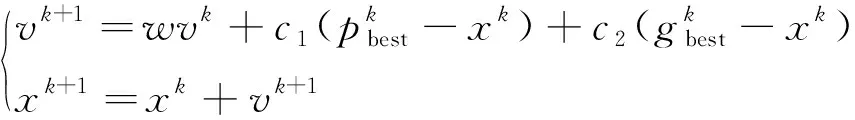
(10)

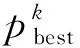
对FAPSO采用经典测试函数Sphere进行验证。Sphere函数表达式如式(11)所示。

(11)

仿真参数设置:在FAPSO算法中设置学习因子c1=c2=2;种群规模popsize=20;惯性权重wmax=0.9,wmin=0.4。仿真结果表明,经PSO算法优化后f(x)最小为3.891×10-3;经FAPSO算法优化后f(x)最小为8.369×10-4。适应度值变化曲线如图3所示,可以看出,FAPSO算法相较于标准粒子群优化算法(PSO)收敛速度更快、种群粒子的全局搜索能力更强、搜索精度更高。因此,本文将采用FAPSO算法对地铁列车节能运行优化问题进行研究。

图3 Sphere函数适应度曲线对比Fig.3 Comparison of sphere function fitness curves

3 列车运行时刻表优化

3.1 列车最小运行时分策略

为提高列车运行图的鲁棒性,列车计划运行时间的设定通常是在最小运行时分的基础上加上一定量的冗余时间。冗余时间通常设置为列车计划运行时间的5%～10%[19]之间。本文将列车站间最小运行时分策略定义为:在列车启动阶段,以最大牵引力牵引列车运行,达到路段限速后匀速运行进入巡航工况,当列车接近终点时,根据列车制动性能以最大减速度制动停车。

3.2 基于FAPSO的冗余时间分配

根据列车最小运行时分策略,计算出总冗余时间,然后通过对列车运行数据拟合[20],获取列车站间运行时间-能耗关系曲线,如图4所示。在该曲线下对总冗余时间分配策略进行理论分析,然后使用FAPSO算法对总冗余时间进行分配,得出各站间最佳运行时间,生成新的列车运行时刻表。冗余时间分配流程如图5所示。

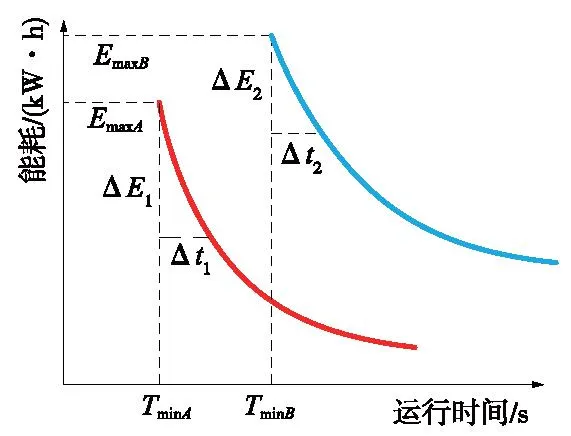
图4 列车站间运行时间-能耗关系曲线Fig.4 Relationship curve between train station operation time and energy consumption

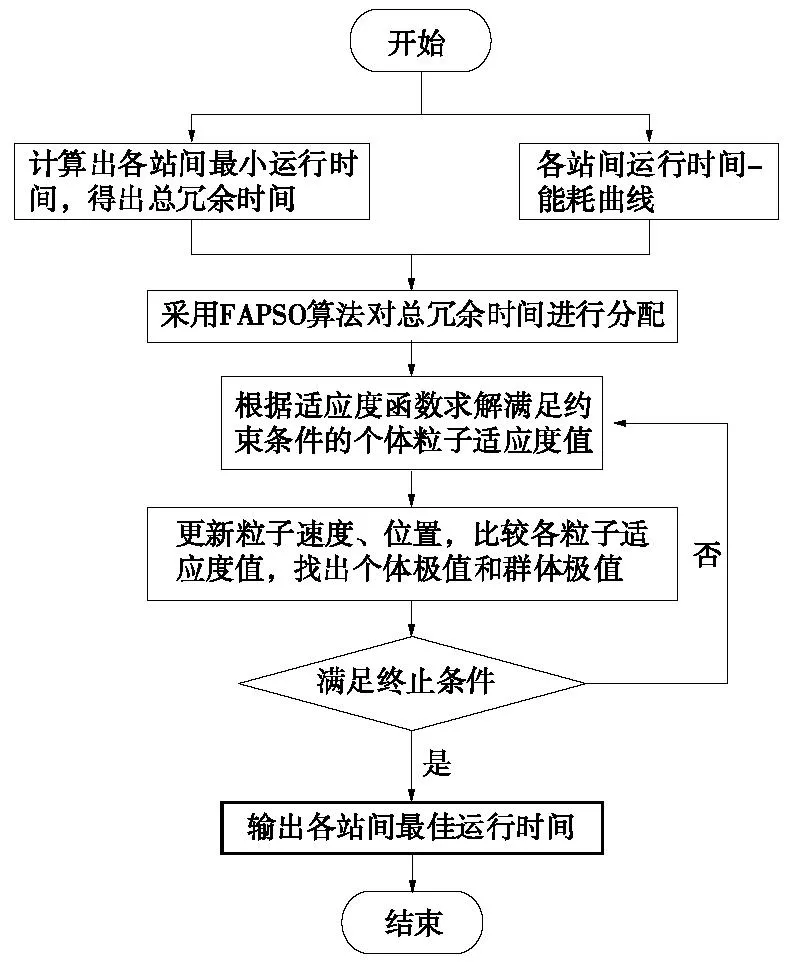
图5 冗余时间分配流程Fig.5 Redundant time allocation process

4 列车运行策略选择

在牵引-巡航-惰行-制动四阶段运行策略中,通常列车牵引到推荐速度后进入巡航工况,而列车长时间处于巡航工况下,其运行能耗较大[21]。为减少列车运行能耗,在给定运行时间下,通过在列车巡航工况状态下插入合适的“牵引-惰行”工况,使列车充分惰行,以此降低列车运行能耗。如图6所示,将列车运行策略分为图6(a)插入一次牵引-惰行工况转换点,图6(b)插入多次牵引-惰行工况转换点。对这2种不同的列车运行策略,再次使用FAPSO算法搜索最佳惰行工况转换点插入的位置。通过对不同运行策略下列车运行能耗对比,获得列车站间最优运行方案,实现列车节能、准点运行的目标。

图6 列车运行策略Fig.6 Train operation strategy

5 实例仿真

选用中车株洲生产的B2型车作为仿真车型,以广州地铁某段线路数据为基础进行仿真实验。列车主要参数特性和线路参数分别如表1、表2所示。AB站间长1 120 m;BC站间长1 908 m;CD站间长2 172 m;A站到D站列车计划运行时间357 s,列车实际运行时间为347～367 s,误差为±10 s。

表1 B2型车主要参数特性Table 1 Main parameters and characteristics of B2 train

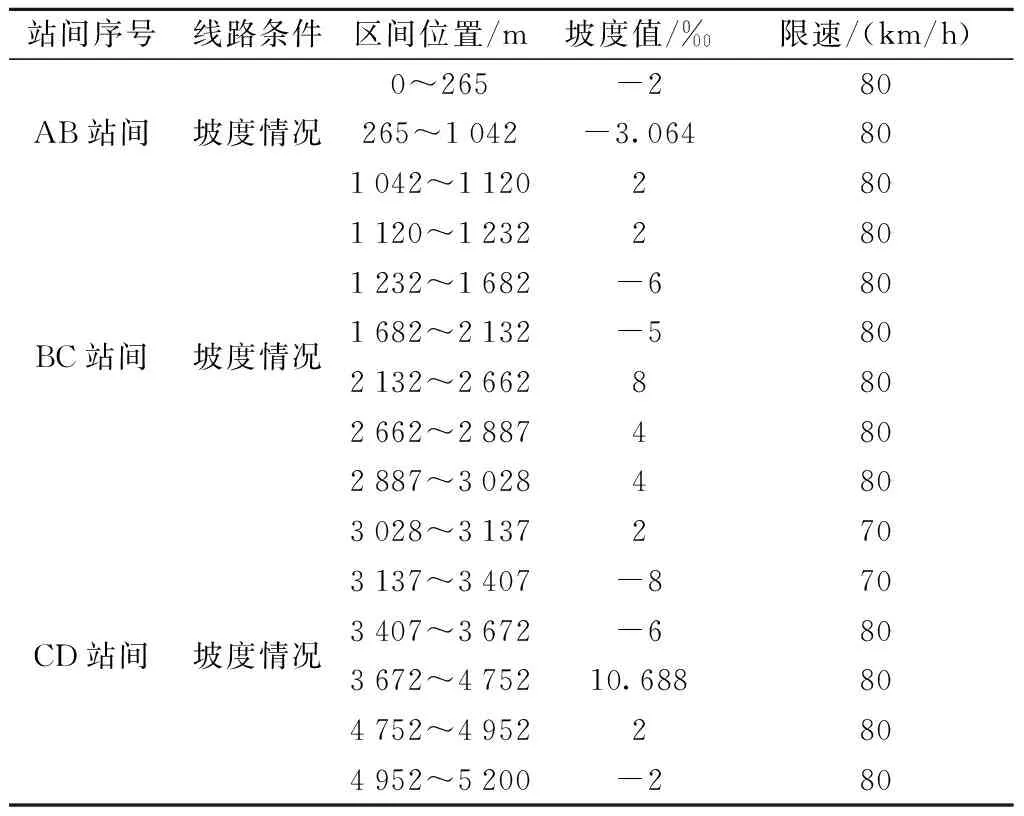
表2 线路参数Table 2 Line parameters

在满足列车安全运行的前提下,采用牵引-巡航-惰行的运行模式,对AB、BC、CD三站间通过MATLAB仿真得到未优化前的列车运行速度曲线,如图7所示。

在双层结构一体化优化中,先选取AB站间使用MATLAB对列车运行数据进行拟合,获得列车站间运行时间-能耗关系曲线,如图8所示。剩余站间采用相同方法得到该曲线,然后根据实际线路数据和列车计划运行时间,分别求出各站间最小运行时间,如表3所示。以列车各站间最小运行时间为基础,对列车实际运行时刻表进行分析,得出总冗余时间。在满足列车总运行时间不变的前提下,上层优化使用FAPSO算法对总冗余时间进行分配,优化列车运行时刻表。优化后,3个站间最佳运行时间分别为87.64,129.14,142.82 s,总运行时间为359.6 s,与总计划运行时间357 s偏差2.6 s,在误差允许范围内。

表3 列车各站间运行时间 sTable 3 Running time between train stations

图8 AB站间列车运行时间-能耗曲线Fig.8 Running time energy consumption curve of AB interstation trains

基于上层优化所获得的站间最佳运行时间,分别对(a)插入一次牵引-惰性工况、(b)插入多次牵引-惰性工况两种不同运行策略下列车站间运行能耗进行对比,从而为各站间选择最优运行方案。各区间在不同驾驶策略下列车运行能耗如表4、表5所示。

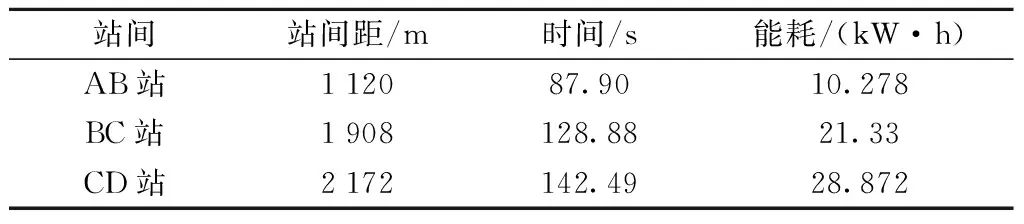
表4 (a)运行策略下列车站间运行能耗结果Table 4 Energy consumption results for operation between stations under (a) operation strategy

表5 (b)运行策略下列车站间运行能耗结果Table 5 Energy consumption results for operation between stations under (b) operation strategy

从表4、表5数据可以看出,列车站间运行策略可由不同站间运行距离进行调整。在站间距离较大的区间使用(b)运行策略节能效果更好,但在站间距离相对较小的站间,若仍使用(b)运行策略,则节能空间不足。因此,在较短运行区间使用(a)运行策略可有效减少列车运行能耗,在较长运行区间使用(b)运行策略节能效果更好。综上,经双层结构一体化优化后,站间AB采用(a)运行策略,站间BC、CD采用(b)运行策略列车总运行能耗最小,且总运行时间与计划运行时间357 s仅相差3.82 s,在偏差允许范围内。仿真数据如表6所示。优化后,列车总运行能耗减少10.8%,且满足列车准点运行的要求,各站间列车节能运行速度-距离曲线及对应的工况转换序列分别如图9、图10所示。

表6 优化前、后列车运行指标Table 6 Train operation indicators before and after optimization

图9 各站间最优运行策略下速度-距离曲线Fig.9 Speed distance curves under optimal operation strategy between stations

图10 列车各站间工况转换序列Fig.10 Conversion sequence of train operating conditions between stations

6 结论

针对地铁列车节能运行优化问题,首先建立了多质点列车模型,并将萤火虫算子引入到标准粒子群算法中,采用双层结构一体化优化控制方法,在上层优化中对列车运行时刻表进行优化,得出各站间最佳运行时间;下层优化在此基础上,对列车不同运行策略进行优化,并比较其运行能耗,进而为各站间筛选出最佳运行方案,指导列车节能、准点运行。

(1)多质点模型相比于单质点模型,对分析列车运行过程中所受附加阻力的变化更符合实际情况,且更为准确。

(2)本文采用的FAPSO算法相比于PSO算法其收敛速度更快,搜索精度更高,经该算法求解后可以在满足列车准点运行的前提下,较好地达到列车节能运行的目标。

(3)以广州地铁站间线路为例进行实例仿真,使用双层结构一体化优化控制方法,优化后列车总运行能耗减少10.8%。因此,在实际工程应用中具有很好的指导作用。

(4)本文仅考虑了单列车的节能运行优化问题,并未考虑在实际情况下站间运行列车往往不止一辆,针对多列车追踪的运行优化问题,需要进一步研究。