基于粗糙集理论和Delphi 法的卫星平台指标优化研究
2024-01-18韦国军齐分岭何能波陈玉龙
侯 炜,韦国军,齐分岭,2,何能波,陈玉龙
(1.航天工程大学,北京 102206;2.解放军66389 部队,太原 030031)
0 引言
指标是对卫星平台进行综合评价的前提,在指标构建过程中,由于主观因素较多[1],要考虑到指标的全面性、科学性,指标可能会存在重复、等价等情况,会不同程度地造成评价模型维数过高、求解复杂,可能还会对评估结果产生干扰,所以,需要用科学的方法对评价指标进行优化筛选。传统的指标优化方法有很多,比如:专家评分法、层级分析法、回归分析法、主成分分析法等。其中,专家评分法、层次分析等方法主要考虑评价者的主观想法较多,容易出错;回归分析法、主成分分析方法需要大量样本支持,数据是对装备的综合评价,评价过程缺乏大量数据供于运算和分析。以上方法都是针对不同系统的特定指标进行评估,虽然关注点和侧重点各有不同,且有许多可取之处,但运用在平台指标优化中的适应性并不强。
1 某型卫星平台指标
指标是活动的核心,是科目设计、数据采集及评估的依据,构建科学合理的指标体系对于有效开展工作具有十分重要的意义[2],因此,应先构建指标体系。同时,在按照指标逻辑逐层分解的基础上,考虑部队用户需求和前期试验过程中重要、需要被持续关注的指标,以获得初步的、具有一定指导性的指标体系。通过基于映射分解的方法,设计了某型卫星平台基础指标,构建出37 个基础指标,初步构建了卫星平台指标体系,由于保密要求,故不列出具体指标体系图,仅给出优化过程和具体算法,在后续的优化过程中,一些敏感指标用字母代替。
2 粗糙集理论
粗糙集是一种基于统计理论的知识挖掘方法,是一种处理不完整、不精确问题的数学理论。该理论的优点是其完全以数据为驱动型,即不需要除了信息系统以外的任何先验知识[3]。

那么同理,在集合U 中,把同样具有等价关系的IND(R)的集合称作等价类,即:
其中,U| IND(R),在后续为了方便统一记作U|R,是对应到集合U 的一个划分,表示为:
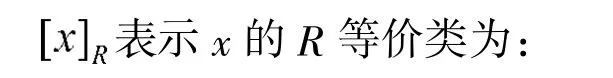

可以明显看出上近似和下近似存在的不同之处,上近似表示的等价类中的任一元素x,它既有可能属于集合X,又有可能不属于集合X;而下近似表示的等价类中的任一元素x,它肯定是属于集合X 的。
根据等价关系IND(R)的上近似以及下近似,可以知道集合U 可以划分为3 个毫无交集的区域,称作正域POSR(X)、负域NEGR(X)以及边界域BNRR(X)。
其中,
综上可知,POSR(X)的所有对象肯定包含于集合X,即X 肯定包含POSR(X);NEGR(X)的对象一定不包含于集合X;边界域BNRR(X)则是不能确定其对象是否包含于集合X 的集合。


通过属性约简的集合被称为属性约简集,在约简集当中属性个数最少的那个约简集被称为最小约简集,优化问题一般都是寻找最小约简集的过程[5]。
2.1 实例分析
以某型卫星装备适编性为例进行实例分析。该型卫星装备适编性由3 个二级指标和9 个三级指标构成,利用粗糙集的方法对9 个三级定性指标进行优化。在研究指标过程中,邀请相关专家对初始指标进行了打分。根据粗糙集需要对数据进行离散化的要求,将指标分为4 个等级[6],相对应每个等级为1~4 分,如表1 所示。

表1 指标参数等级表Table 1 Index parameter grade list
在制作出指标参数等级表后,结合部队专家打分情况,得出每个指标具体的分数和等级,也就是将指标数据离散化。共收集了10 组数据,并且以此建立指标信息表,如表2 所示。通过表2,可以分别得出论域U,条件属性C 以及决策属性D,其中。论域U 是指标的10 份样本。条件属性,是指指标质量要素集,决策属性。根据粗糙集理论,需要根据条件属性C 以及决策属性D 得出论域U 的等价类:
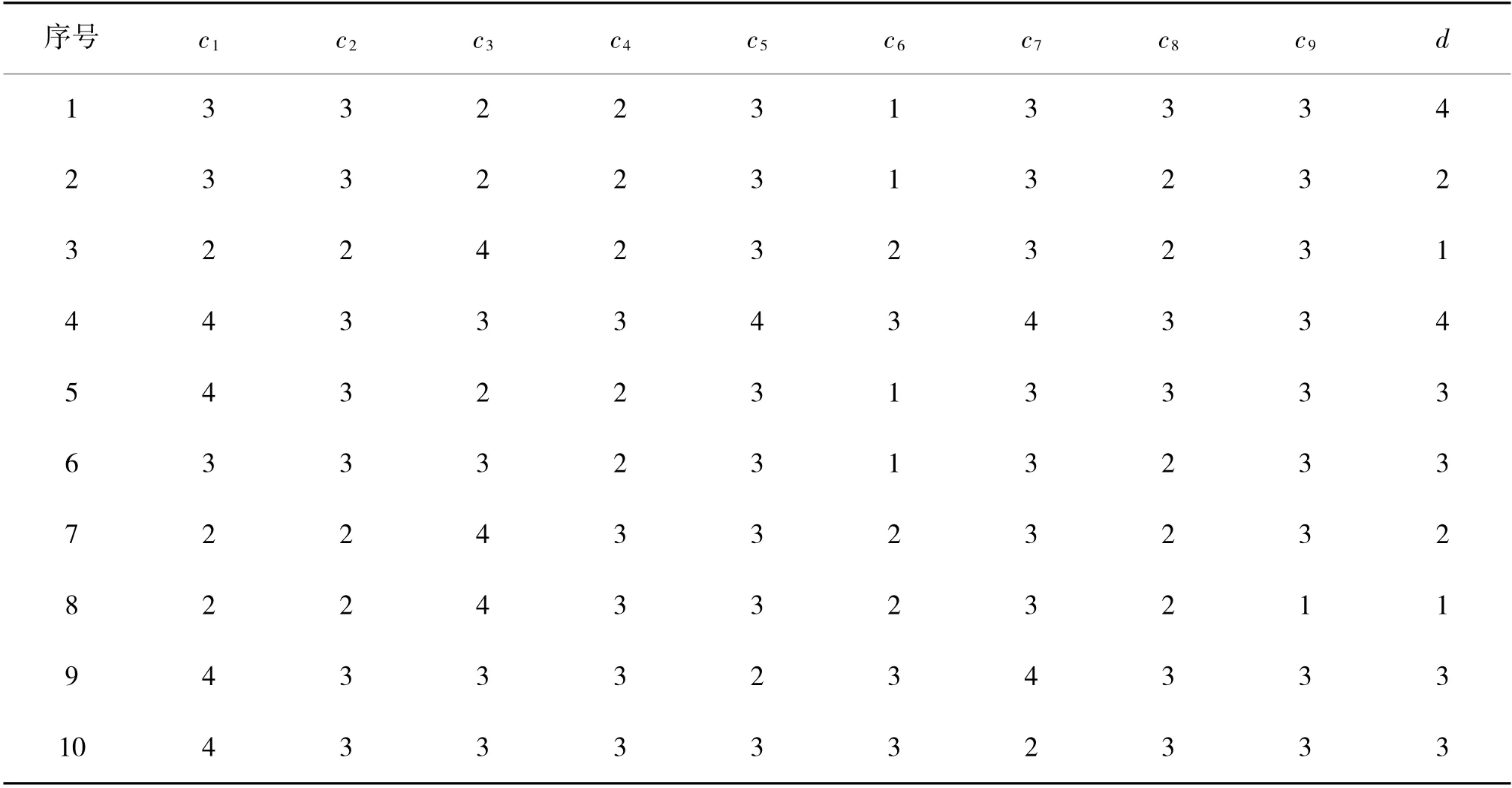
表2 卫星平台指标信息表Table 2 Satellite platform index information list

那么,c1为C 集合中的必要指标,应当予以保留。
那么,c2为C 集合中的不必要指标,应当可以去除约简。
那么,c6为C 集合中的不必要指标,应当可以去除约简。
由于篇幅限制其他计算过程省略。

2.2 指标检验
指标优化完成后,要通过对指标的检验来验证指标优化是否科学,这里利用Kruskal-Wails 检验法进行检验。Kruskal-Wails 检验法是要根据所检验的数据进行有序排列,计算每个数据的秩,同时要计算每组数据的和,根据公式求KW 的值。
其中,Ni为每组样本总个数;Ri为该组秩的和;n 为所有数据的总数;k 为组的数量。倘若在计算的样本中存在具有相同秩值的数据,那么还需要利用校正系数C 对相应的KW 的值进行校正。
计算得出KW'的值后,利用检验表对各组数据的显著性差异进行判断,从而检验了指标优化的科学性。将未进行优化的9 个指标和优化后的7 个指标输入SPSS 软件进行KW 非参数检验,得出未优化的9 个指标的显著性是0.157,优化后的7 个指标的显著性是0.104,表明经过优化后,每个指标的信息载荷量更大,独立性更强,说明利用粗糙集理论对卫星平台基础指标优化是合适的,也是有效的。同理,根据粗糙集理论对改型卫星整个指标体系进行优化,共得到34 个优化后的指标。
3 基于Delphi 法的卫星平台指标体系优化
第2 章通过粗糙集理论,对卫星平台指标进行了优化。然而,在优化后,该指标体系可能还存在不符合部队实际的情况,需要将优化后的指标体系提交部队专家,进行是否具有可操作性和实际指导意义的讨论,也就是说粗糙集理论优化只能说明科学性的问题,而指标体系的合理性还需要通过部队专家结合平台实际使用情况进行二次优化。
3.1 Delphi 法简介及指标优化流程
Delphi 法最早运用于20 世纪50 年代美国预测其受到原子弹袭击后可能出现的糟糕结果,十几年之后,美国兰德公司将Delphi 法运用于技术预测之中,后来迅速传播。Delphi 法的通用性非常强,几乎可以运用于任何场景和领域。其本质上就是通过匿名征询领域内专家意见,进行归纳总结、整理统计,再匿名反馈给上述专家,经过多次征询,直到得到稳定的结果[7]。
本文中利用Delphi 法通过多次反复征求部队专家和一线部队意见,对之前已经用数学方法优化的指标体系进行完善及开展合理性验证。其流程为:
1)科学遴选专家组成员,尽量涵盖平台的所有过程;
2)根据已经优化的指标体系建立咨询表,并将指标构建过程及前期优化方法进行说明;
3)咨询专家对于指标体系构建意见,并对指标进行打分;
4)收集汇总咨询表,对于专家意见的一致性进行评判;
5)如遇到分歧,将分歧意见反馈至专家,并开展多轮的意见征求,最终要达到意见的统一;
6)综合处理所有专家的意见,并完成指标体系的最终优化。
重点要关注咨询表的设计,指标不能存在歧义,不得干扰专家进行指标评判,同时咨询轮数不宜过多。
3.2 评判意见一致性


得出方差和S 后,结合上文提出的m 个部队专家对于n 个指标进行的重要度排序,m 个部队专家意见的一致性程度用来表示。其中,C.I.称为一致性系数,0≤C.I.≤1,若一致性系数C.I.越接近于0,则表示部队专家的意见越不一致;若C.I.越接近于1,说明多数的部队转件的意见趋向一致;如果达到1,则表示部队专家的意见完全一致。
3.3 确定指标重要性

3.4 卫星平台指标二次优化
在前期已经利用粗糙集对平台指标体系优化的基础上,利用Delphi 法再次进行优化,进一步加强平台指标体系的合理性,使构设的指标体系被用户部队认可,具有一定的实用性[8]。
首先成立平台指标专家组。邀请5 名有丰富岗位经验的专家成立专家咨询组,专家岗位分别从卫星总体设计、试验鉴定部门、平台使用单位、平台运行管理维护单位和平台管理部门的行政管理(装备部门)5 个岗位之中各挑选一名[9]。职称为高职3名,中职1 名,行政岗位专家为上校。
制作咨询表。表内共罗列优化后的34 个指标,要求专家依据指标重要程度按照1~34 的顺序对指标进行打分,并对专家讲清规则:若认为此指标对于平台指标体系影响最小,则打分为1 分,若认为此指标对于平台指标体系影响最大,则打分为34分。在这两者区间则视情打分为2~33 分,以此类推,分数不能重复[10]。

根据经验C.I.的值如果不低于0.85,则可以表示专家意见已经达成了一致。那么计算每轮咨询的C.I.值,若在0.85以下,则继续下一轮咨询,若达到0.85,则停止咨询。本次共开展4 轮专家咨询和意见征求,每轮根据专家意见对指标进行修改与调整后发送专家进行下一轮咨询,4 轮专家咨询的C.I.值分别为0.396 548、0.579 942、0.805 496、0.869 194,由于研究集中性要求和篇幅限制,本文只给出最终的专家评分情况,如表3 所示。
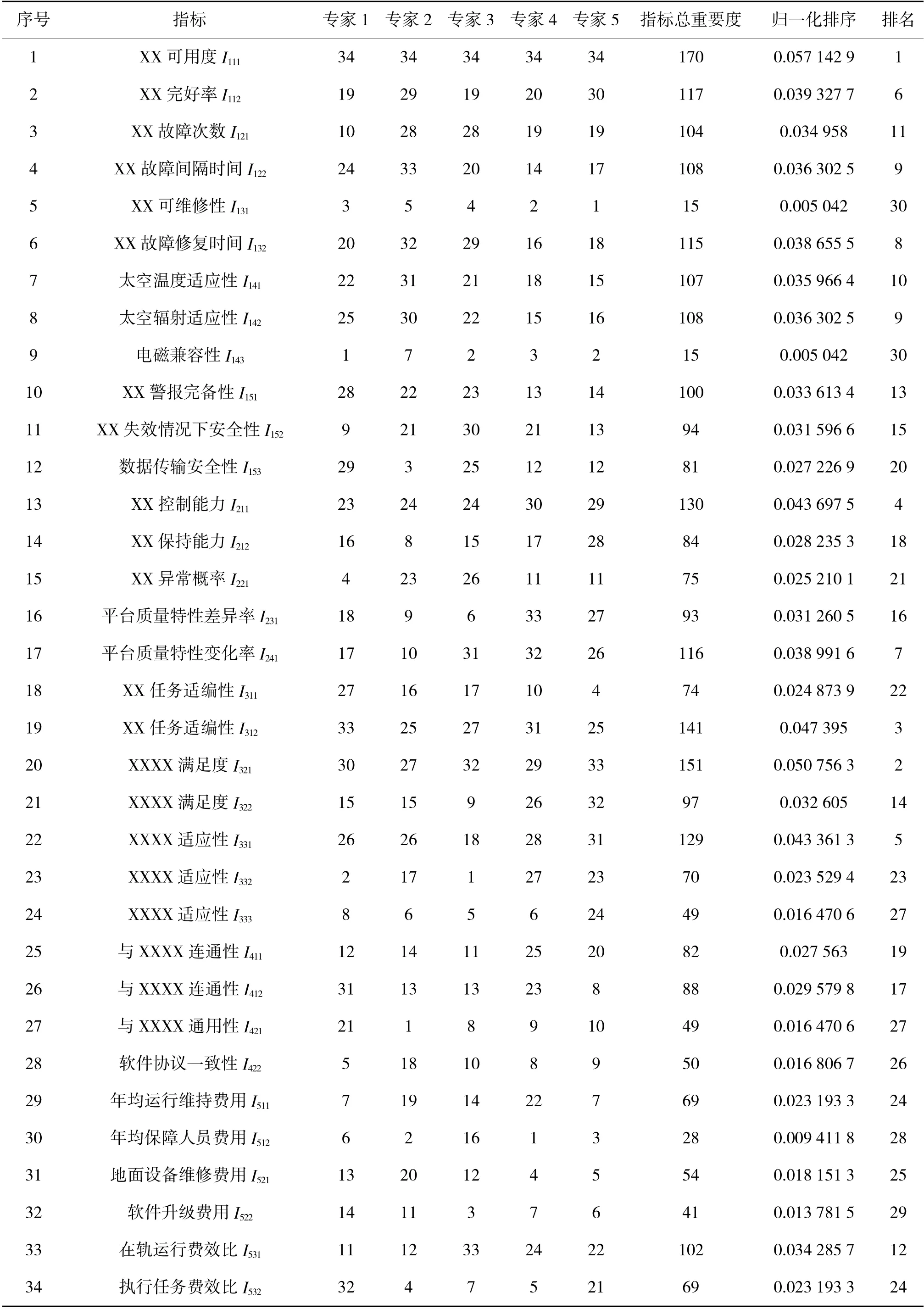
表3 专家评分汇总表Table 3 Expert scoring summary table
根据专家打分汇总,对卫星平台指标体系共34个三级指标进行归一化处理和排序,并通过计算得出总重要度排名,从重要度第1 名的指标项开始累加,当累加到第30 项指标时,N=0.966 722 689≥a(a经过考虑,取0.96),那么最后的4 个指标I131、II143、I522和I512通过优化被舍弃。该卫星平台最终指标体系分为5 个二级指标和30 个三级指标。
4 结论
本文对某型卫星平台指标体系进行优化研究。利用粗糙集理论对指标进行内部的独立性和信息载荷量进行优化,是对指标体系是否具备科学性进行探讨;利用Delphi 方法对指标是否被用户部队认可、是否具有实用性进行优化,是对指标体系的合理性进行探讨,通过两次优化使卫星平台指标体系具有一定的参考价值。也表明指标最终还是要回归指导实践,在构建优化过程中要充分尊重用户部队意见的思想。
